运动补偿对机载SAR重轨干涉成像的影响分析

方东生,吕孝雷,李缘廷,李芳芳,钱 江

(1.中国科学院电子学研究所空间信息处理与应用系统技术重点实验室,北京100190;2.中国交通通信信息中心,北京100011;3.电子科技大学,四川成都611731)

0 引言

机载重轨干涉SAR具有非常高的分辨率和良好的机动性,可以根据地物观测的需要灵活地选择波段和飞行平台,重轨干涉能满足L、P等较长波段对基线的要求,在局部地区的地形测绘[1-4]、形变监测[5-6]上具有非常重要的意义。然而机载系统由于平台易受气流干扰,实际运动轨迹往往偏离预定理想轨迹,无法保证稳定的基线要求,这为实现高精度的重轨干涉测量提出了严峻的挑战。

相对于常规的单航过机载SAR成像,重轨干涉SAR的成像为保证基线的稳定,两次航过的成像需要选择相互平行的参考轨迹进行成像。机载平台易受气流的影响导致轨迹往往偏移预定轨迹,多次航过轨迹可能偏移较大甚至交叉,成像处理中通过“搬移”将两次飞行数据沿着两条平行的参考轨迹作运动补偿。目前机载干涉SAR成像时采用基于IMU/DGPS测量数据[7-9]的运动补偿方法,其相位准确性不仅取决于IMU/DGPS测量数据的精度,还依赖于运动补偿算法本身引入的残余误差。许多研究者的工作集中在研究单轨SAR运动误差对成像的影响和高精度的运动补偿方法。文献[10]主要分析了IMU测量误差导致的残余误差对机载SAR成像的影响;文献[11-12]讨论了波束中心近似引入的残余误差对重轨干涉SAR性能的影响,为运动补偿精度的估计提供了技术支持;文献[13]定量分析了由IMU/DGPS测量误差和DEM误差引入的残余误差对正侧视情况下机载SAR成像的影响,并进一步分析了其对重轨干涉的影响;文献[14]从成像斜距历程误差建模,分析了由于平地假设和导航精度引入的残余运动误差,但其并未考虑误差对成像的影响。在研究高精度的运动补偿方法方面,许多子孔径运动补偿方法(如 SATA[15]、PTA[16]、FD[17])被相继提出,此类方法旨在减小波束中心近似和平地假设引入的方位空变和地形依赖的运动误差对成像的影响,但此类方法并未定量分析残余误差量对重轨干涉的影响。

目前少有文献定量地分析基于“搬移”的模型对重轨干涉成像造成的影响。在基于FFT成像算法的框架下,分析了由于搬移成像引入的残余误差量对干涉成像的影响,并进一步分析了对重轨干涉测量的影响,为机载重轨干涉性能分析提供了一定的理论基础。

1 机载SAR搬移成像模型

图1是建立在正交坐标系x-y-z下的机载重轨SAR搬移成像几何模型。两轨飞行中,轨迹2飞行的真实轨迹与轨迹1并不平行。目前基于FFT的成像方法是将轨迹2按照与轨迹1平行的参考轨迹成像,其中搬移产生的偏移量主要通过在成像中嵌入包络移动和相位补偿来实现运动补偿。轨迹2由于搬移的影响,相对于成像参考轨迹也会引入一个斜视角,令β为波束中心斜视角,d为载机在方位y′位置时天线APC真实位置A(y′)相对于成像参考轨迹上A′(y′)处的偏移量,该偏移量位于与参考航迹垂直的平面,与水平面的夹角为α(详细的几何意义可见成像交轨向剖面,如图2所示),θ为下视角。P0(r0,y Pd)表示波束中心处散射点,y Pd=y′+yd0,Pd(r,y Pd)表示位于波束中心上,且与P(r,y)具有相同最近斜距的散射点。

图1 机载SAR搬移成像几何模型

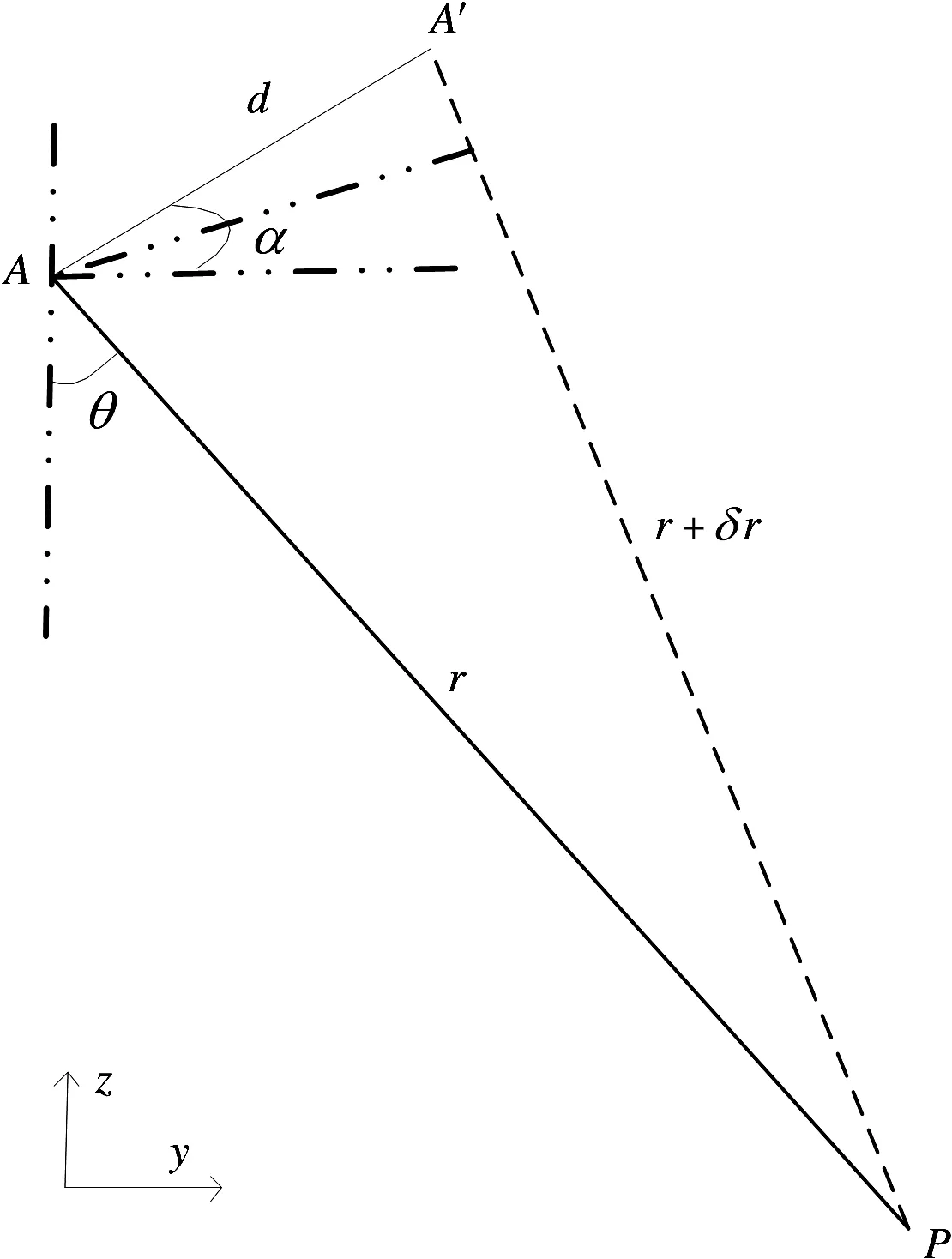
图2 SAR成像交轨平面

对场景中任何一散射点P(r,y),对于P点的真实瞬时斜距表示为

成像时P点相对于参考轨迹的瞬时斜距为

P点成像时的真实误差为

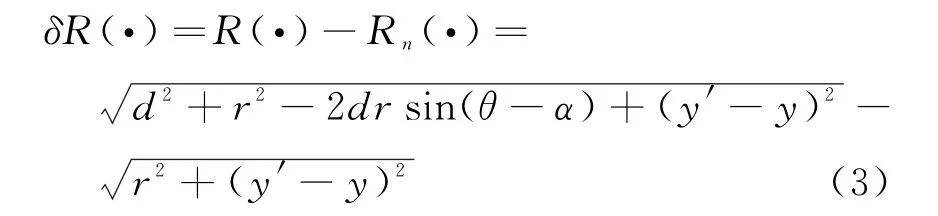
对于波束中心线上的P0(r0,y′)点,真实瞬时斜距为

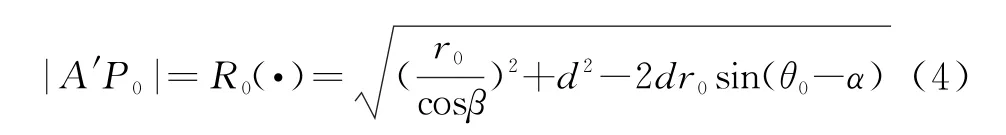
相对于参考轨迹的瞬时斜距为

Pd(r,y Pd)点的真实瞬时斜距为

相对于成像参考轨迹的瞬时斜距为

运动补偿有许多方法,传统的一级、二级运动补偿量[7]能在推导中比较直观地表达,而且也是目前比较基本的补偿方法,子孔径成像算法[15-18]等补偿精度模糊,故此处采用基本的两级运动补偿方法,以方便下面的分析。

对于P(r,y)点,采用波束中心近似进行一级运动补偿,补偿的误差量为

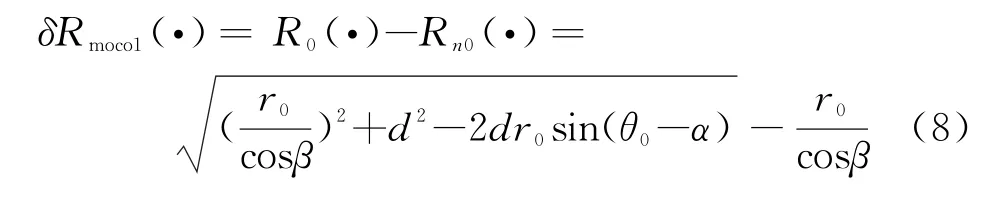
二级运动补偿补偿距离空变的误差量,对于P点的补偿量为

两级运动补偿总共补偿的残余误差量为

经过一级和二级运动补偿之后的残余量为

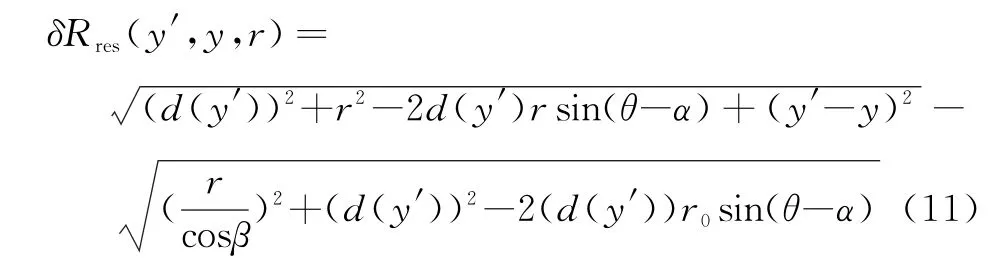
由式(11)可见,残余误差中存在距离和方位空变的耦合误差。由于速度不一致导致的影响可以通过重采样过程来消除,不在此处讨论。以下分析仅从搬移补偿导致的斜距误差来推导。

假设雷达发射脉冲宽度为T、调频率为Kr的线性调频信号,对于点目标P(r,y),接收到的回波经解调后可以表示为

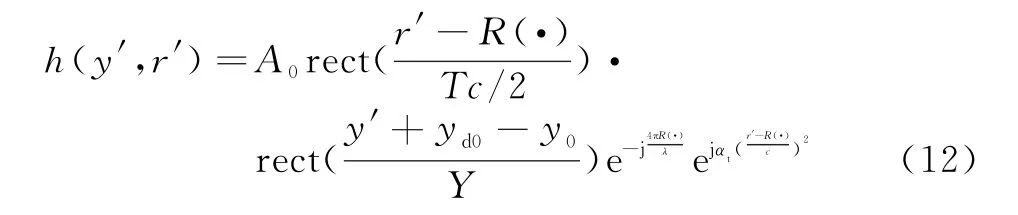
式中,αt=4πKr,yd0=tanβ·r0,yd0由搬移导致的微小斜视角β引起,Y表示合成孔径长度,R(·)表示天线运动位置y′处到目标的距离。为了继续分析“搬移”运补对成像的影响,“搬移”产生的轨迹偏移误差最终转换为斜距误差影响目标的成像。斜距表示为

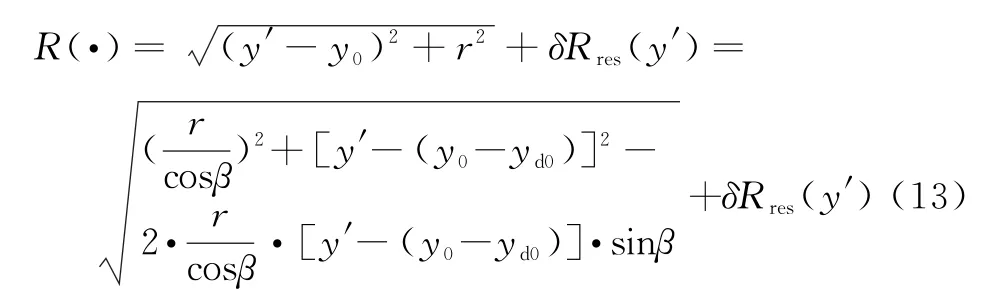
将上式根号项进行泰勒展开,得

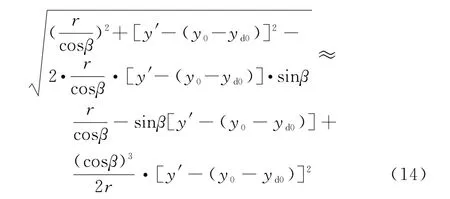
式(14)中表现出了距离徙动[19],其中一次项为距离走动,二次项表现为距离弯曲。

假设波束中心的斜距误差为二次斜距误差[13],Taylor展开到二次项,则

对解调后的信号进行距离压缩,并变换到二维频域为

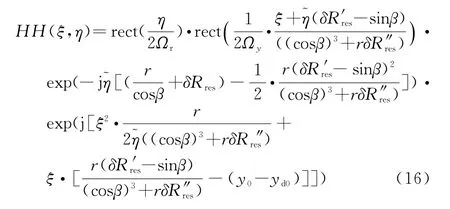
式(16)表现了在搬移运动补偿残余为线性和二次误差情况下经距离压缩之后的信号二维频谱。其中,为方位带宽。频谱在方位向由于搬移导致的斜视角和残余误差而有频移,方位带宽也会随之改变。最后一个指数项中的二次项依赖于二次残余误差和斜视角,指数项中的一次项与残余误差的一次项、二次项及斜视角均相关。

2 考虑搬移后运动补偿残余误差的影响

运动补偿残余误差的耦合性会使进一步的分析复杂化,下面分别考虑了搬移后运动补偿残余误差的线性误差项、二次误差项,分析了其对成像和干涉的影响。

2.1 线性误差的影响

如果δRres(·)中仅仅考虑常数项和线性项,代入式(16)为

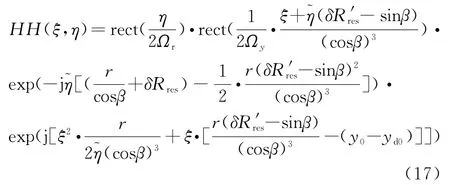
经过距离徙动矫正(RCMC)和方位压缩后,最终可得聚焦后的显示表达式:

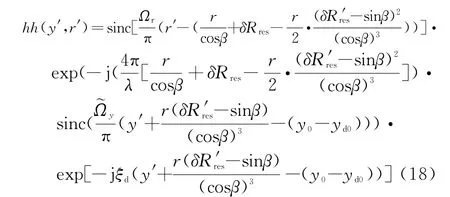
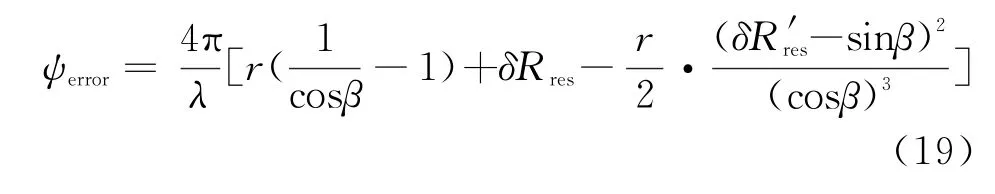
附加相位误差与残余误差和斜视角均有关系,给干涉测量精度带来影响,具体分析见2.3节。

残余误差中的常数分量和一次分量影响图像聚焦后的压缩位置,导致目标定位误差和图像畸变。搬移成像后,目标方位压缩位置偏移量为

距离向偏移量为

压缩后的偏移量均与搬移产生的斜视角β有关。一种直观的解释是,获取回波信号的坐标系同成像处理坐标系间存在偏转角,而且存在斜距的残余误差量,成像处理将信号转换到成像坐标系下,从而引起图像定位偏差。偏移量的大小受残余量和斜视角同时影响,如果搬移角度较大,残余误差量较大,图像压缩后偏移量也会变大,这给重轨干涉SAR图像配准带来困难。

2.2 二次误差的影响

仅仅考虑残余δR res(·)中的二次相位和常数项，则

通过RCMC和方位压缩之后,最终推导结果为

式中:

从推导结果可以看到,残余误差中的二次残余量造成距离向主瓣位置上出现了方位向压缩残余误差,将导致一定程度的方位向散焦,引起压缩后旁瓣的不对称。为了说明二次项的影响,存在残余误差项和不存在残余误差项成像之后点目标压缩结果对比如图3所示,图3中显示出方位冲击响应剖面图。二次误差主要影响目标方位向的聚焦,导致不同程度的散焦和IRW展宽,误差较大时将导致目标的完全散焦。

图3 存在二次残余误差时目标压缩的影响

2.3 相位误差对重轨干涉的影响

下面分析由一次分量引入的相位误差对重轨干涉的影响。

假设搬移角度较小,忽略较小的斜视角,令β=0,则压缩后的结果为

由于机载系统斜距r一般在1×104～1×105m量级,对于δRres在1×10-3m,δR′res在1×10-3～1×10-4量级,其压缩后距离向位置偏移量级与δRres一致,而方位向偏移量可达米级,这也是机载重轨干涉SAR图像配准困难的原因,而且分辨率越高配准越困难。主、辅图像配准后同一像素的相位分别表示为ψm和ψs:

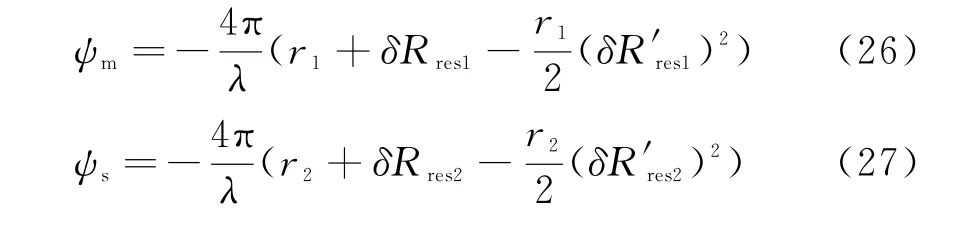
由残余误差引入的干涉相位误差为

机载双天线干涉SAR由于基线刚性连接,残余误差量往往可以在一定程度上抵消,从而获得较高的反演精度;对于机载重轨干涉,由于几次航过的残余误差独立,产生的干涉相位误差项φerro可能比单轨成像的相位误差还要大,这将严重制约高程反演精度。特别是对于不具备高精度自动驾驶仪的国内平台来说,载机平台将会以大幅度的运动误差偏离预定航线,残余误差项δRres将会变得更大,成为制约机载重轨干涉精测量度的因素之一。

由于干涉处理环节较多,此处仅考虑残余误差相位项对重轨干涉的影响(忽略基线去相关、噪声去相关等导致的配准误差和相位解缠误差等),则反演的高程误差量为

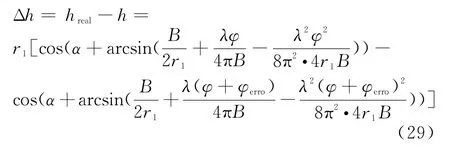
为了形象地说明干涉相位误差的量级,结合C波段重轨干涉SAR(波长0.055 5 m),飞行高度在8 000 m左右,基线B为80 m,斜距在10 000 m左右,对于主图像残余误差一次项δR′res1从-0.001线性变化到0.001,辅图像残余误差一次项δR′res2从0线性变化到0.002。对于r1=7 818.43 m,r2=7 778.2 m的目标进行分析,不考虑其他干涉处理环节引入的误差(配准误差、相位解缠误差等),其产生的干涉相位误差量与高程反演误差关系如图4所示。从图4可以看出,不考虑去相关的影响,仅附加相位误差对高程反演的误差就可达到米级,这也是重轨干涉测量中不容忽视的误差源。

残余相位误差也会影响方位向的相位,图5给出了没有残余误差和存在一次相位误差下的点目标幅度响应和相位响应,由于相位误差的影响,目标压缩后的相位斜坡也会发生变化。相位斜坡的变化也从侧面反映了附加相位误差的存在。

图4 高程反演误差

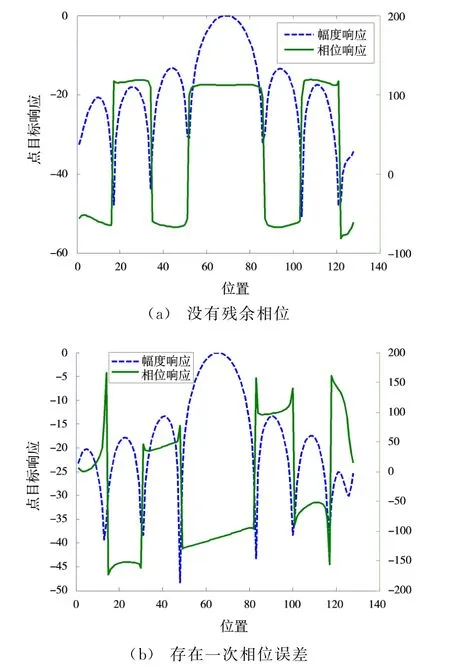
图5 没有残余相位和存在一次相位误差影响下的点目标方位向幅度响应和相位响应

图6给出了绝对相位误差与一个孔径内运动补偿残余的关系。如果要保证单次成像的绝对误差要控制在π/8以内,则一个孔径内的平均残余误差量δRres应该控制在5.5 cm以下;而对于重轨干涉,为了保证干涉相位误差控制在π/8以内,则对于每次航过搬移成像的平均残余误差量δRres的控制要比5.5 cm更小。

图6 绝对相位误差与一个孔径内运动补偿残余的关系

3 仿真分析

为了说明理论推导的正确性,下面通过仿真实验来说明。

仿真SAR系统参数如表1所示。仿真中采用3个点目标,位置设定在参考斜距处,如表2所示。

表1 仿真SAR系统参数表

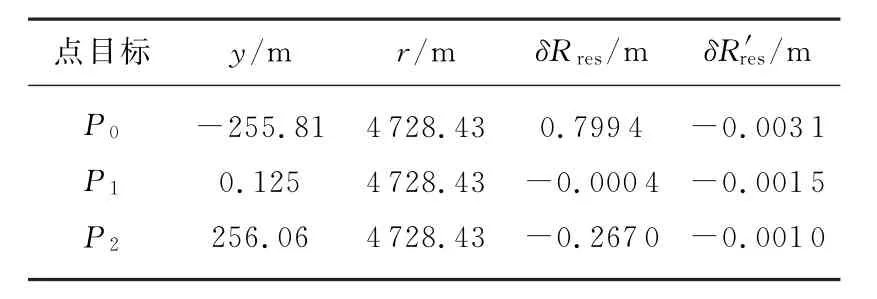
表2 仿真点目标的位置及残余误差系数

首先直接在斜距误差中加入运动误差,各个点目标的斜距残余误差的常数项和线性项误差如表2所示,方位、距离采样点数量分别为4 096和2 048。成像时目标位置采用压制零多普勒的方法,仿真后的点目标位置经过8倍升采样,然后取峰值位置作为压缩后的位置。在不同小斜视角(0°,1°,1.5°)情况下理论推导的目标压缩位置偏移量、仿真后实际的位置偏移量如表3所示。对比分析可以发现,理论推导的压缩位置偏移量和仿真真实的位置偏移量之间的差异不超过0.5个像素,说明斜距误差模型对分析残余误差的有效性。

表3 不同斜视角情况下线性残余误差下的点目标压缩位置

然后考虑成像轨迹相对于实际轨迹搬移和运动补偿引入斜距误差的影响,方位、距离采样点数量分别为8 192和4 096。由于搬移产生了运动误差,此处采用传统的二级运动补偿方法进行补偿成像。对于每个点目标,可以计算出搬移后运动补偿量和实际需要补偿的误差量,然后获得运动补偿后的残余误差量。文中的推导采用了将补偿导致的残余误差量在波束中心处泰勒展开的形式进行,此处将不同点目标的残余误差在其一个孔径内数值拟合,求出常数误差项、线性误差项和二次误差项。在搬移不同角度(0.5°,1°,1.5°,2°)情况下理论推导的位置偏移量、仿真后实际获取的位置偏移量如表4所示。仿真点压缩位置的偏移随着搬移引入的误差的增大而变大。为了方便比较误差影响下目标压缩质量,成像时方位、距离均不加窗。表5从3 dB IRW,PSLR,ISLR指标上比较了不同搬移角度下点目标压缩质量。理论上点目标3 dB IRW为0.46 m,由于搬移引入的残余误差,点目标IRW均展宽,PSLR,ISLR等指标也随着搬移误差的增大而增大。

仿真中成像轨迹相对于原始轨迹搬移不同角度(0.5°,1°,1.5°,2°),导致的交轨偏移量如图7所示,搬移运补之后引入的相位误差如图8所示,假设第一轨数据没有相位误差,基线长为33 m,基线角为1.28°。仿真点目标的最终反演的高程误差如图9所示。从仿真结果中可以看出:搬移角度越大,运动补偿产生的残余误差就越大,相位误差就越大,高程反演的误差就越大。

表4 搬移不同角度情况下点目标压缩位置

表5 搬移不同角度下的点目标压缩质量(距离、方位均没加窗)

对于重轨干涉SAR成像,选择平行的参考轨迹往往需要通过搬移一定的角度来实现。从以上的仿真中可以看出,搬移不同的角度对应着不同的运动补偿残余误差量,该误差量不仅影响图像压缩位置和压缩质量,而且带来附加相位误差,该附加相位误差直接影响到重轨干涉高程反演精度,该因素是制约重轨干涉精度的重要因素,必须在运动补偿算法中考虑相应的算法来减小它的影响。或者通过在平台上搭载高精度的飞控系统,以便提高飞行的稳定性,减小重复飞行轨迹相对于参考轨迹的搬移误差量,提高重轨干涉测量的精度。

图7 不同搬移角度对应的交轨向偏移量

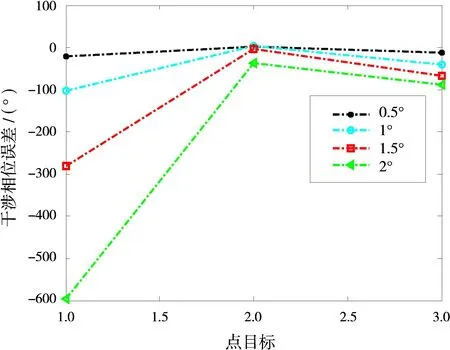
图8 不同搬移角度下仿真点成像引入的相位误差

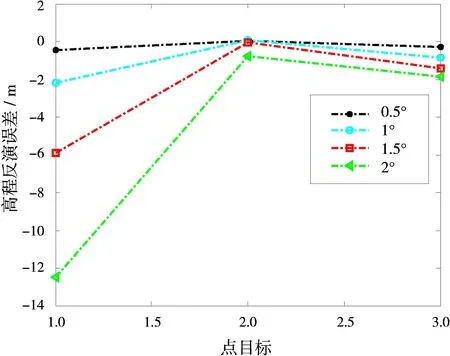
图9 不同搬移角度下仿真点高程反演误差

4 结束语

本文针对机载SAR飞行轨迹偏移的问题,定量分析了由于搬移成像导致的残余误差对干涉成像的影响,详细推导和讨论了残余一次和二次误差的影响,并通过仿真验证了理论分析的正确性。可以得到以下结论:机载重轨干涉SAR飞行轨迹相对于成像轨迹偏移越大,成像时搬移和运动补偿后残余量越大,引入的相位误差越大;高精度的重轨干涉测量必须尽量减小由于搬移引入的残余误差,必须保持飞行轨迹尽量接近于成像参考轨迹,以减小干涉相位误差。本文的分析结果为定量分析重轨飞行的搬移成像对机载重轨干涉的影响提供了理论依据,从聚焦后的相位准确性的角度对机载重轨干涉平台提出了要求:机载系统必须具备高精度的自动控制和调整飞行轨迹的能力,以满足基线要求和减小残余误差对干涉性能的影响。

[1]徐华平,陈杰,周荫清,等.干涉SAR三维地形成像数据处理技术综述[J].雷达科学与技术,2006,4(1):15-21.XU Huaping,CHEN Jie,ZHOU Yinqing,et al.A Survey of Interferometric SAR Topography Mapping Data Processing Technique[J].Radar Science and Technology,2006,4(1):15-21.(in Chinese)

[2]GRAY A L,FARRIS-MANNING P J.Repeat-Pass Interferometry with Airborne Synthetic Aperture Radar[J].IEEE Trans on Geoscience and Remote Sensing,1993,31(1):180-191.

[3]HENSLEY S,KLEIN J,ROSEN P,et al.Repeat Pass Aircraft Interferometry Results at Portage Lake,Maine and Innisfail,Australia[C]∥The Sixth Annual JPL Airborne Science Workshop,Pasadena,CA:NASA,1995:9-33.

[4]REIGBER A,ULRICHT A.P-Band Repeat-Pass Interferometry with the DLR Experimental SAR(E-ESAR):First Results[C]∥International Geoscience and Remote Sensing Symposium,Seattle,WA:IEEE,1998:1914-1916.

[5]HENSLEY S,ZEBKER H,JONES C,et al.First Deformation Results Using the NASA/JPL UAVSAR Instrument[C]∥2nd Asia-Pacific Conference on Synthetic Aperture Radar,Xi’an:IEEE,2009:1051-1055.

[6]HENSLEY S,ZEBKER H,JONES C,et al.Use of Airborne SAR Interferometry for Monitoring Deformation of Large-Scale Man-Made Features[C]∥International Workshop Spatial Information Technologies for Monitoring the Deformation of Large-Scale Man-Made Linear Features,Hong Kong:ISEIS,CUHK,2010.

[7]MOREIRA A,HUANG Yonghong.Airborne SAR Processing of Highly Squinted Data Using a Chirp Scaling Approach with Integrated Motion Compensation[J].IEEE Trans on Geosciences and Remote Sensing,1994,32(5):1029-1040.

[8]REIGBER A,ALIVIZATOS E,POTSIS A,et al.Extended Wavenumber-Domain Synthetic Aperture Radar Focusing with Integrated Motion Compensation[J].IEEE Proceedings-Radar,Sonar and Navigation,2006,153(3):301-310.

[9]KIRK J C.Motion Compensation for Synthetic Aperture Radar[J].IEEE Trans on Aerospace and Electronic Systems,1975,11(3):338-348.

[10]MAO Yongfei,XIANG Maosheng,WEI Lideng,et al.The Effect of IMU Inaccuracies on Airborne SAR Imaging[J].Journal of Electronics(China),2011,28(4):409-418.

[11]FORNARO G,FRANCESCHETTI G,PERNA S.On Center-Beam Approximation in SAR Motion Compensation[J].IEEE Geoscience and Remote Sensing Letters,2006,3(2):276-280.

[12]李银伟,邓袁,向茂生.波束中心近似对机载干涉SAR运动补偿的影响分析[J].电子与信息学报,2014,36(2):415-421.

[13]FORNARO G,FRANCESCHETTI G,PERNA S.Motion Compensation Errors:Effects on the Accuracy of Airborne SAR Images[J].IEEE Trans on Aerospace and Electronic Systems,2005,41(4):1338-1352.

[14]林雪,李芳芳,胡东辉,等.平地假设与残余运动误差对机载重轨干涉SAR系统性能的影响分析[J].雷达学报,2013,2(3):334-347.

[15]PRATS P,REIGBER A,MALLORQUI J J.Topography-Dependent Motion Compensation for Repeat-Pass Interferometric SAR Systems[J].IEEE Geosciences and Remote Sensing Letters,2005,2(2):206-210.

[16]DE MACEDO K A C,SCHEIBER R.Precise Topography-and Aperture-Dependent Motion Compensation for Airborne SAR[J].IEEE Geosciences and Remote Sensing Letters,2005,2(2):172-176.

[17]ZHENG X,YU W,LI Z.A Novel Algorithm for Wide Beam SAR Motion Compensation Based on Frequency Division[C]∥IEEE International Symposium on Geosciences and Remote Sensing,Denver,CO:IEEE,2006:3160-3163.

[18]ROSEN P A,HENSLEY S,WHEELER K,et al.UAVSAR:A New NASA Airborne SAR System for Science and Technology Research[C]∥IEEE Conference on Radar,Verona,NY:IEEE,2006:24-27.

[19]保铮,刑孟道,王彤.雷达成像技术[M].北京:电子工业出版社,2004:130-132.