一发多收MIMO雷达的目标关联特性

朱丽芳,任翠霞,李 军,谢菊兰,刘静秋

(1.电子科技大学电子工程学院,四川成都611731;2.桂林电子科技大学信息与通信学院,广西桂林541004)

0 引言

作为一种新体制雷达,多输入多输出(MIMO)雷达有着诸多的特点和优势[1-3],目前学术界根据天线配置方式的不同将MIMO雷达划分为两大类[4]:分布式和集中式。分布式MIMO雷达的天线在空间内分散放置,能够利用目标散射特性的差异获取空间分集增益,较大程度地克服目标RCS在空间的起伏特性;集中式MIMO雷达的天线中各子阵天线间距较小并集中放置,能够同时进行收发波束形成,充分利用收发阵列孔径,形成“空间扩展效应”。

两类MIMO雷达并非是对立的,双基地MIMO雷达可以构成了子阵级分布式系统[5-6],联合分布式和集中式的工作特点,兼有两者的性能优势。T/R-R模式MIMO雷达是典型的一发双收双基地雷达系统,属于最简单的雷达组网结构。为了充分发挥出雷达组网的优势,各个部分必须协调一致工作。雷达组网中一些必须考虑的关键技术有:时间空间同步技术、信息融合技术、目标跟踪技术[7]、干扰定位技术[8]等。其中信息融合是至关重要的一步,它直接影响雷达组网性能优势发挥的程度,而目标关联[9-11]是信息融合的前提。若目标关联出现错误,将会导致雷达组网定位跟踪效果反而不如单部雷达。

文献[12]从测量误差较小和检测概率较大这两个方面指出MIMO雷达在目标关联过程中的优势,但只是简单的介绍,并没有给出关联的具体过程和概率分析。文献[13]针对雷达和红外的航迹关联性能进行了分析和评估,推导出给定正确关联概率时的错误关联概率以及给定错误关联概率时的正确关联概率。文献[14]基于二维指派航迹关联算法,讨论了天基光学被动跟踪系统的航迹关联问题,建立了检验统计量的概率分布模型。虽然文献[13]和文献[14]关于目标关联的分析比较全面,但都不是基于MIMO雷达跟踪系统讨论的。MIMO因其自身的特点,目标关联与普通跟踪系统有诸多不同,然而至今笔者还鲜有见到专门分析MIMO雷达目标关联特性的文献。本文基于最近邻关联算法,建立了T/R-R模式双基地MIMO雷达系统目标关联的概率模型,以两目标为例推导了正确关联概率;分析了信噪比、目标位置以及目标间隔的影响;并与普通相控阵的目标关联进行了对比,验证了MIMO雷达定位精度较高带来的目标关联性能上的优势。

1 信号模型

T/R-R模式的MIMO雷达是典型的一发双收雷达系统,以T/R-R模式双基地雷达为研究背景,收发天线都采用均匀线阵,收、发阵元数分别为M,N。该系统的几何配置如图1所示,基线长为L,直角坐标系的原点选在T/R站处,发射站(T/R站)、接收站以及目标构成双基平面。

图1 T/R-R模式几何配置图

本文以p个静默的点目标作为研究对象,下面给出回波模型[2]。各个发射通道的信号以s i(t)(i=1,…,M)表示,脉冲宽度为Tp,各通道信号相互正交,将发射信号写成向量的形式:

分析可知,T/R站实际上相当于一个集中式MIMO雷达,若T/R站发射阵元数为M,接收阵元数为N,则T/R站处第k个目标的回波信号可表示为

式中,ηTk为与T/R站收发过程有关的传输系数,τTk为发射阵列与目标的收发双程传输延时,目标序号k=1,…,p,at(θTk)=[1,e-jφtTk,e-j2φtTk,…,e-j(M-1)φtTk]T为 发 射 阵 列 导 向 矢 量,φtk=2πdtsin(θTk)/λ,ar(θTk)=[1,e-jφrTk,e-j2φrTk,…,e-j(N-1)φr Tk]T为 接 收 阵 列 导 向 矢 量,φrk=2πdrsin(θTk)/λ,发射信号波长、发射单元之间的间隔、接收阵元之间的间隔分别为λ,dt,dr,VT(t)为N维高斯白噪声矢量。

R站则相当于一个普通双基地MIMO雷达,设接收阵元数仍然为N,阵元间隔仍然为dr,则R站目标回波信号可表示为

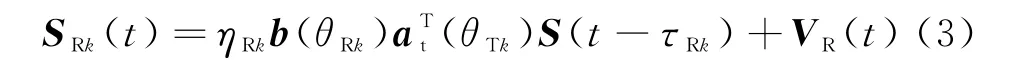
式中,ηRk为与R站收发过程有关的传输系数,τRk为R站收发过程传输延时,b(θRk)=[1,e-jφrk,e-j2φrk,…,e-j(N-1)φrk]T为接收阵列导向矢量,φrk=2πdrsin(θRk)/λ,VR(t)为N维高斯白噪声矢量。

对回波信号进行匹配滤波、波束形成等一系列处理,可估计回波信号延迟从而得到目标距离,采用集中式MIMO雷达测角方法和双基地MIMO雷达测角方法可分别测得发射角和接收角。总的来说,T/R-R模式双基地的测量参数如表1所示。

表1 T/R-R模式双基地雷达的测量参数

2 目标关联决策

T/R-R模式双基地MIMO雷达的T/R站实际上相当于一个单基地MIMO雷达,R站相当于一个普通收发分置的MIMO雷达,收发分置MIMO雷达不仅可以测接收角,还可以测发射角,出现信息冗余,对冗余信息进行优化融合,可以大大地改善基线区、发射站、接收站的定位精度。

由上节信号模型可知,T/R站可测得参数(RT,θTT),设测量误差为(ΔRT,ΔθTT);R 站可测得 参 数 (RS,θR,θTR),设 测 量 误 差 为 (ΔRS,ΔθR,ΔθTR)。测角、测距误差均方根分别为σθ,σR,其与信噪比以及收发站相关参数之间的关系可由文献[15]给出。

对于T/R站可直接利用两个测量参数对目标的位置进行估计[16]:

目标位置误差与测量误差之间的关系为

式中,BT为式(4)对(RT,θTT)的雅克比矩阵,定位精度为

对于R站,存在信息冗余,可从3个测量参数中选出两组测量子集(RS,θR),(RS,θTR),分别进行定位,然后对两组定位结果按照加权最小二乘法[16]进行信息融合,得到精度更高的定位结果:

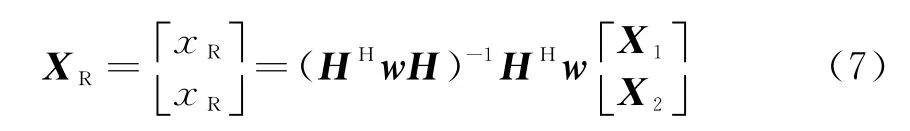
式中,H=[I I]T是二维单位矩阵,加权矩阵w=两组测量子集的定位结果X1,X2、对应的协方差矩阵P1,P2,以及对应的雅克比矩阵F1,F2,均可由文献[16]求得,那么目标位置误差与测量误差之间的关系为

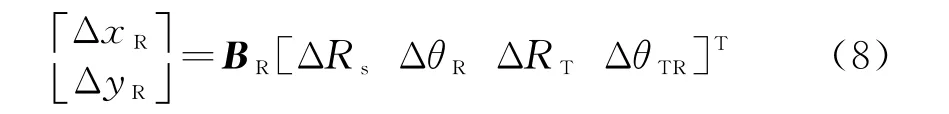
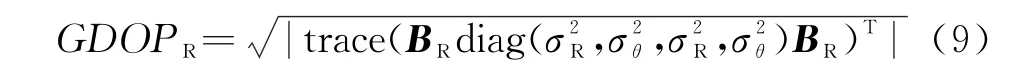
按照经典最近邻算法[17]进行关联判决,可设检验统计量为

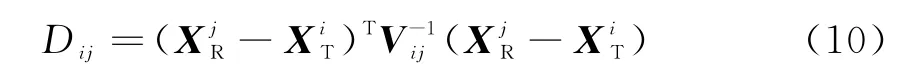
式中,i,j为发射站、接收站所对应的目标序号,设i=j时表示收发站观测到的是同一个目标,V ij为的协方差矩阵。关联门限为K,那么D ij≤K则说明序号为i,j的目标关联成功,反之关联失败。当一个目标与另一个接收站的多个目标同时关联成功时,取检验统计量小的作为最终的关联结果。

3 关联概率分析

理论上目标的位置估计值应由两部分组成,其一为目标位置的真值,其二为由测量误差引起的目标位置的误差,那么序号为i,j的目标位置之差也由两部分组成,其一为目标位置真值差d xij,d yij,其二为位置误差之差,结合式(5)和式(8)可知:

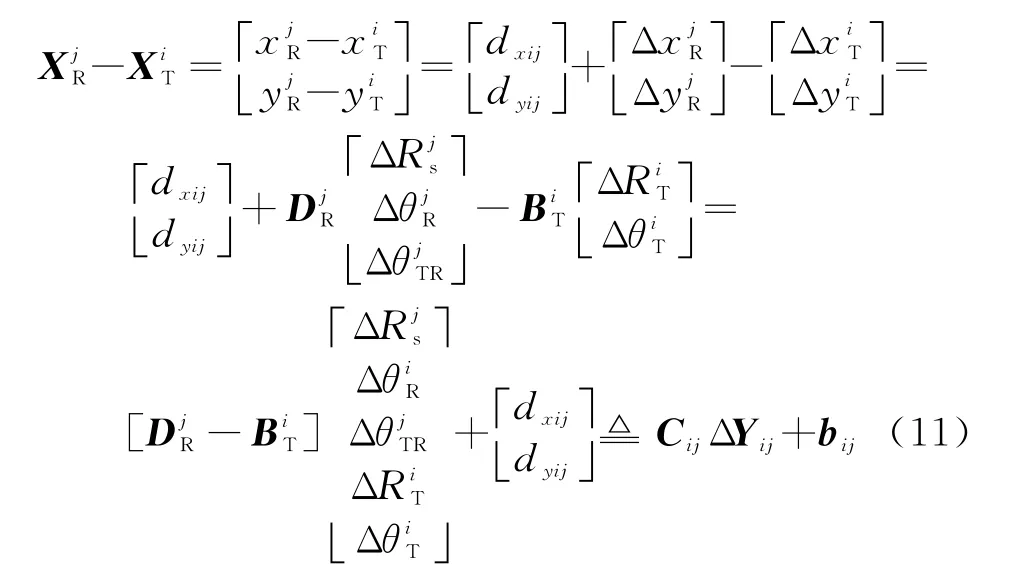
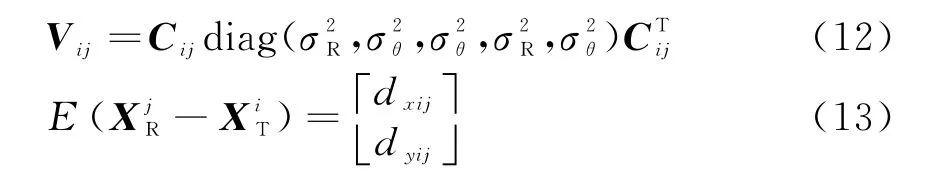
根据文献[9]可知D ij可近似为自由度为2的非中心的卡方分布,即D ij～χ2(2,δij),其中偏离度δij可知当i=j时,即D ii服从自由度为2的卡方分布。门限K可通过卡方分布D ii的分位点来求得。那么序号为i,j的目标关联成功的概率为

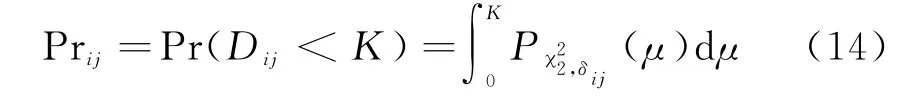
若考虑两个目标的关联问题,对于序号为1的目标,正确关联的概率为

式中,Pr(D12＞D11)可通过将D12/D11建模为非中心的F分布,门限取为1来得到。

4 双基相控阵雷达目标关联

T/R-T/R模式相控阵雷达,每个站相当于一个单基地雷达系统,都只能测得目标视线角和距离,相比于MIMO雷达不存在定位信息冗余,定位精度较差,也必将导致目标关联的不够准确。其目标关联的统计量同样可以建模为非中心卡方分布,即D Xij～χ2(2,δXij)。

5 仿真验证

为了验证本文所提出的定位精度的提高给MIMO雷达目标关联带来的好处,一方面进行了蒙特卡洛仿真,来计算正确关联的概率,另一方面采用文中建立的概率模型计算正确关联概率的理论值,此外还分析目标间隔、目标位置,以及信噪比对正确关联概率的影响。

研究目标位置对关联概率的影响时,仿真条件为:基线长25 km,发射信号带宽4MHz,发射波束3 d B宽度7.8°;输出信噪比取为25 d B;目标1位置变化时,目标2的横坐标始终与目标1的相差100 m,纵坐标与目标1相同。

图2给出了两种模式副站定位精度的对比,可以看到,除基线区外,MIMO模式的定位精度在一定程度上高于相控阵模式的定位精度,其给目标关联概率带来的影响如图3所示,同样除基线区外,MIMO模式的正确关联概率在一定程度上高于相控阵模式的正确关联概率,验证了文中所提到的MIMO雷达系统在目标关联方面的优势。

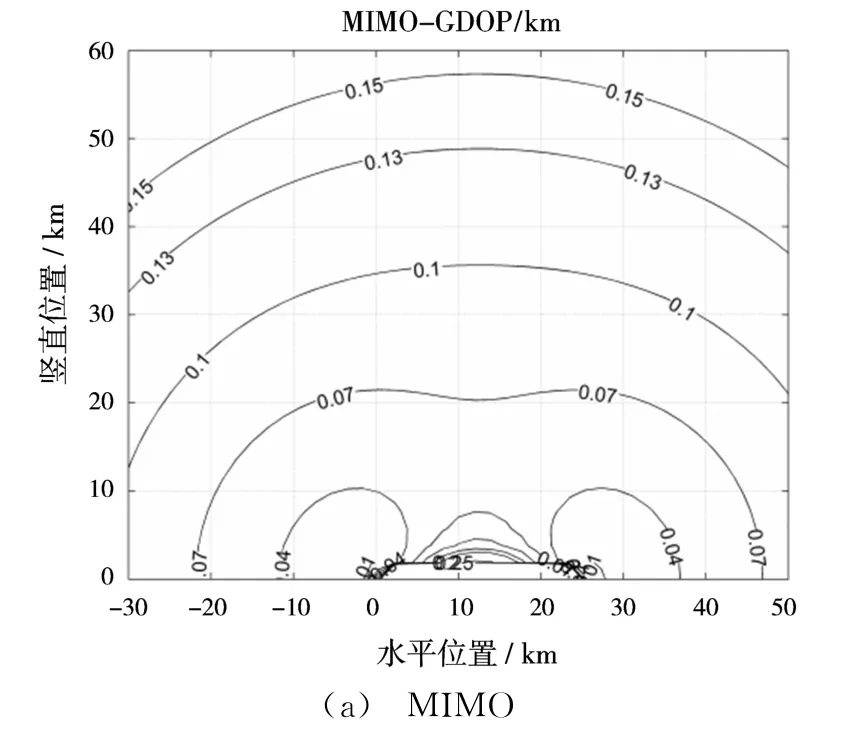
图2 两种模式接收站的定位精度对比

图3 两种模式正确关联概率在双基地平面上的等值线

研究目标间隔对关联概率的影响时,目标1的位置固定为(35 km,45 km),目标2的位置与1有一定的偏差Δ,为(35 km+Δ,45 km),其中Δ在(0,500 m)范围内变换,其他条件不变。

仿真结果如图4所示,可见采用文中所建概率模型得到的关联概率理论值与仿真值很接近。此外,还可以看到,当目标间隔为100 m时,MIMO雷达正确关联概率可达0.9左右,而相控阵只有0.6左右;MIMO雷达在间隔为150 m时关联概率基本上可以达到1,而相控阵的在间隔为400 m时才接近1。可见MIMO雷达的关联性能优于相控阵,这正是因为MIMO雷达的接收站可以测得发射视线角,出现信息冗余,定位精度较高。

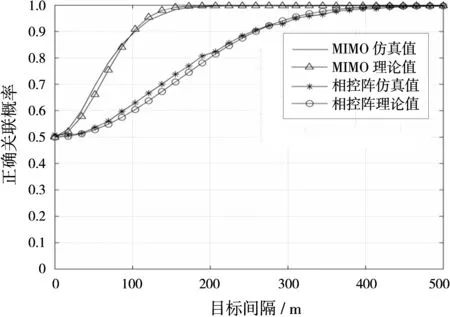
图4 目标间隔变化时正确关联概率

研究输出信噪比对目标关联的影响时,信噪比在(0,50)d B范围内变化,目标间隔固定为100 m,其余条件不变。仿真结果如图5所示,输出信噪比为25 dB时,MIMO雷达正确关联概率约为0.9,相控阵仅约为0.6,而且MIMO雷达的正确关联概率在30 d B左右时达到1,相控阵雷达在40 d B时才达到1。输出信噪比影响的是测量参数的测量误差,信噪比高时,测量误差较小,定位精度也有所提高,目标关联精确度提高。

图5 输出信噪比变化时正确关联概率

6 结束语

由于MIMO雷达发射相互正交的信号,回波信号中含有发射站角度信息,接收站可以独立测得发射视线角,出现信息冗余,融合后定位精度明显提高,目标关联的准确性也随之明显提高。基于此,本文针对MIMO雷达系统的目标关联,建立概率模型,推算正确关联概率,并进行了性能分析。仿真验证了概率模型的正确性,且通过与普通相控阵雷达对比,突出了MIMO雷达在目标关联方面的性能优势:其一,同等条件下正确关联概率大大提高,其二,随着信噪比或者目标间隔的变化,MIMO雷达的正确关联概率能够较快地达到1。文中虽然着重以T/R-R模式的MIMO雷达系统的静默点目标关联为例,但是本文所建立的概率模型以及所得到的结论,同样适用于多目标多基地MIMO雷达系统的航迹关联问题,可作为分布式MIMO雷达组网关联问题的理论依据,具有重要的实际意义。

[1]RABIDEAU D J,PARKER P.Ubiquitous MIMO Multifunction Digital Array Radar[C]∥37th Asilomar Conference on Signal,Systems and Computers,Pacific Grove,CA:IEEE,2003:1057-1064.

[2]何子述,韩春林,刘波.MIMO雷达概念及其技术特点分析[J].电子学报,2005,33(12A):2441-2445.

[3]陈慧,邵怀宗,潘晔,等.基于稀疏表示的频控阵MIMO雷达多目标定位[J].雷达科学与技术,2015,13(3):259-264.CHEN Hui,SHAO Huaizong,PAN Ye,et al.Multiple Targets Localization in Sparse Representation-Based Frequency Diverse Array MIMO Radar[J].Radar Science and Technology,2015,13(3):259-264.(in Chinese)

[4]陈浩文,黎湘,庄钊文.一种新兴的雷达体制:MIMO雷达[J].电子学报,2012,40(6):1190-1198.

[5]刘红明,何子述,王荣海.一种基于MIMO技术的多基地防空雷达系统[C]∥雷达网第17届年会暨雷达技术应用研讨会,福州:信息产业部雷达专业情报网,2007:61-68.

[6]CHONG C Y,PASCAL F,OVARLEZ J P,et al.MIMO Radar Detection in Non-Gaussian and Heterogeneous Clutter[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(1):115-126.

[7]李丽,邱天爽.双基地MIMO雷达目标参数估计及动态跟踪新算法[J].信号处理,2014,30(2):155-162.

[8]陈金立,朱艳萍,顾红,等.双基地MIMO雷达的高速运动目标定位方法[J].系统工程与电子技术,2013,35(5):962-967.

[9]康健,李一兵,林云,等.基于证据理论的联合概率数据关联算法[J].系统工程与电子技术,2013,35(8):1620-1626.

[10]李猛,王智,李元实,等.角度传感网络多目标定位的数据关联算法[J].电子学报,2014,42(10):1887-1893.

[11]鹿传国,冯新喜,孔云波,等.多无源传感器去相关数据关联算法[J].自动化学报,2014,40(3):497-505.

[12]KRAUT S,BLISS D W.Analyzing the Impact of MIMO Radar on Tracking Association Error[C]∥7th Sensor Array and Multichannel Signal Processing Workshop,Hoboken NJ:IEEE,2012:161-164.

[13]王国宏,毛士艺,何友.雷达和红外航迹关联性能的评估[J].电子与信息学报,2002,24(12):1917-1924.

[14]盛卫东,王博,安玮,等.分布式被动传感器轨迹关联算法性能分析[J].系统工程与电子技术,2010,32(12):2516-2519.

[15]杨振起,张永顺,骆永军.双(多)基地雷达系统[M].北京:国防工业出版社,1998.

[16]孙仲康,周一宇,何黎星.单(多)基地有源无源定位[M].北京:国防工业出版社,1996.

[17]何友,王国宏,陆大琻,等.多传感器信息融合及应用[M].2版.北京:电子工业出版社,2007.