增速传动系统齿轮拍击振动特性研究
2016-01-07沈岗,向东,牟鹏等
第一作者沈岗男,博士生,1989 年8月生
增速传动系统齿轮拍击振动特性研究
沈岗1, 向东1, 牟鹏1, 杨为2, 赵强2
(1.清华大学机械工程系,北京100084; 2.重庆大学机械传动国家重点实验室,重庆400044)
摘要:齿轮的拍击振动效应是增速传动系统复杂动力学特性的重要表征,研究内外部激励对拍击振动的影响,对进一步阐述拍击振动规律具有重要意义。通过搭建一级增速齿轮传动试验台,采用光电编码器和NI 数据采集系统对主动轮和从动轮转速脉冲进行测量和采集,分析主动轮与从动轮的弧长差曲线和转速差曲线,验证了增速传动下的齿轮拍击效应。然后针对不同齿侧间隙与不同转速等试验条件,开展系列化的拍击振动特性研究。分析发现:不同试验条件下的弧长差包络线均呈正弦波动趋势,且其变化幅值随着转速升高而出现缩小的趋势,而弧长差中心线位置的规律性不明显,与齿侧间隙、主动轮转速无关,仅与齿轮副初始位置相关;当拍击效应发生时,随着转速升高,拍击位置具有从齿向往齿背靠近的趋势;随着啮合轮齿间的侧隙增大,相应的拍击门槛转速降低,更易出现拍击振动现象。
关键词:拍击;振动特性;弧长差;侧隙;门槛值
基金项目:国家自然科学基金(51275258) 国家自然科学基金(51078306);国家青年基金项目(51408453);高等学校博士学科点专项科研基金(20106120110004);陕西省自然科学基础研究计划资助项目(2013JQ7007)
收稿日期:2014-01-08修改稿收到日期:2014-04-16
中图分类号:TH132; TH113
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.07.012
Abstract:Gear rattling is an important symbol of complex dynamic characteristics under the condition of speed increasing transmission. Therefore, it is of great significance to investigate the influences of internal and external incentives on rattling and to further elaborate rattling vibration characteristics. A speed increasing test-bed was set up using photoelectric encoder and NI DAS to collect rotating speed pulses. Furthermore, gear rattling phenomenon was verified by analyzing the arc length difference and rotating speed difference between meshing gears. On this basis, a series of rattling experiments were conducted under different initial conditions such as different backlash values and different rotating speeds. The results show the envelope curve of arc length difference is in the form of a sine wave, and its variation amplitude has a narrowing trend with the speed increasing, and its central positionis only related to gears’initial position. Moreover, rattling position has the trend to move from meshing surface to opposite surface with the increase of rotating speed when rattling phenomenon appears. In addition, with the increase of backlash, the corresponding rattling threshold value reduces, namely, rattling phenomenon is easier to appear.
Vibration characteristics of gear rattling in speed increasing transmission system
SHENGang1,XIANGDong1,MOUPeng1,YANGWei2,ZHAOQiang2(1.The Department of Mechanical Engineering, Tsinghua University, Beijing 100084,China;2.State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)
Key words:rattling; vibration characteristics; arc length difference; backlash; threshold value
风电装备制造是关系国家利益和能源安全的战略性产业,受随机风载乃至强阵风的冲击作用,以及风沙和近海盐雾的侵害,关键零部件增速箱的齿轮、轴承、主轴的失效是目前最主要、影响最大的风电装备故障。风机增速箱所处的恶劣工况会造成复杂多变的动力学特性,因此高速端齿轮啮合过程中很可能出现拍击效应。而目前对风机增速箱失效规律的研究还有很大的发展空间,即内部激励与外部激励对关键零部件的点蚀、疲劳、断裂等失效模式作用机理的研究仍然缺乏。
在齿轮动力学中,由于齿侧间隙的存在,齿轮传动不能一直处于理想的啮合状态,而是时而啮合、时而脱离啮合反复碰撞,产生拍击振动现象。目前国内外对拍击振动的研究可以分为两类,即拍击振动理论模型的研究[1-5]和拍击振动试验的研究[6-12]。Seaman等[1]首次讨论了引起拍击振动的原因及其类型,并提出了拍击门槛理论;Comparin等[2]建立了轻载下齿轮拍击的简化动力学方程,并阐述了如何将理论研究的动力学方程用于设计研究;Pfeiffer等[3]研究了拍击振动模型从确定性模型向随机性模型的转换问题;Xu等[4]针对齿轮拍击振动系统的非光滑特性,利用碰撞面上的Poincare 映射分析,得到拍击振动系统Lyapunov 指数的计算方法;Dong等[5]建立了拍击振动分析的集中质量模型,研究了主动轴波动激励下振动特性随负载力矩变化的分岔规律。为了验证拍击理论模型的正确性,对拍击振动规律更深入地了解,国内外学者对拍击振动试验展开了深入的研究。Rocca等[11]进行了周期性间隙波动对拍击振动影响的试验研究,并对拍击理论进行了验证;Ottewill等[12]开展了偏心距和外载荷波动两个因素对拍击动力学响应影响的试验研究。
由于风电装备传动链是增速系统,其动力学特性不同于通常的减速系统动力学特性,但是探究整个增速箱(如两级行星和一级平行传动)动力学特性过于繁琐复杂,因此本文只针对一级增速齿轮传动进行拍击特性研究。
1齿轮拍击振动理论模型
齿轮之间的相互关系有正常啮合、齿背啮合、脱齿、齿面碰撞及齿背碰撞五种状态,不同的相对位置关系所对应的拍击状态是不一样的。齿轮之间的这五种状态可以通过啮合线方向轮齿的相对位置表示:
(1)
式中,s是啮合线方向轮齿的相对位置,cn是齿侧间隙。

图1 单级增速齿轮拍击振动模型 Fig.1 Rattling vibration model of single-stage gears
为了表征齿轮啮合过程中相对位置关系所对应的拍击状态,建立典型的单级齿轮传动系统拍击振动模型,如图1 所示。将两啮合齿轮分别安装在两端刚性支撑的弹性轴中间,以齿轮啮合线为x方向建立坐标系,此坐标系的建立方式可以将系统x方向、y方向及扭转方向的振动解耦。
齿轮啮合时的相对位置可以表示为:
s12=rb2φ2-rb1φ1+x2-x1=Δs+x2-x1
(2)
式中,rb1是主动轮基圆半径;φ1是主动轮转动弧度;rb2是从动轮基圆半径;φ2是从动轮转动弧度;x1,x2是主动轮、从动轮的初始位置。
定义啮合线方向的弧长差为:
Δs=rb2φ2-rb1φ1
(3)
此弧长差公式将用于后续的试验分析中。
2试验平台搭建及方案设计
2.1试验平台搭建
本文搭建了一级增速传动试验平台,分析不同侧隙与不同转速条件下的拍击效应,探究增速传动下的拍击规律。试验用齿轮材料是45 钢,调质处理,精度等级为7 级,具体参数如表1 所示。

表1 试验用齿轮参数
在拍击试验的硬件平台搭建方面,动力源选择松下交流伺服电机、松下交流伺服驱动器A4 系列及MPC08SP 运动控制卡。转速测量元件采用A-LF 型光电编码器对电脉冲信号计数,每脉冲数对应的弧度数为:
(4)
NI 数据采集元件是PCI6602 采集卡,负载端连接磁粉制动器。由于拍击振动复现需要满足轻载工况这一条件,所以制动器的加载值比较小。
在拍击试验的软件平台搭建方面,Labview 是一种程序开发环境,使用的是图形化编辑语言G 编写程序,产生的程序是框图形式。本试验结合PCI6602 采集卡通过Labview 程序进行数据采集、数据分析、数据显示及数据存储。
2.2试验方案设计
为了进一步探讨齿轮拍击振动规律,本文针对不同侧隙与不同转速等条件开展了系列化试验。由表1 可知,试验用齿轮副的标准中心距为76.0 mm,而系列化齿侧间隙在试验过程中不易测量,所以用中心距的系列变动代替齿侧间隙的系列变动。试验中系列化的中心距分别为76.2 mm、76.5 mm、76.8 mm、77.1 mm 及77.4 mm。系列化的主动轮转速分别为60 r/min 、120 r/min 、180 r/min、240 r/min、300r/min、360 r/min 及420 r/min。
试验采集到的转角脉冲信号由于受试验环境的干扰,信号的尖峰噪声比较严重。而简单的缩小采样频率,虽然能解决部分尖峰信号问题,但是在其他位置会出现额外的尖峰信号,因此处理结果不够理想。本文采用一阶低通滤波法和限幅滤波法对采集的数据进行综合处理。
一阶低通滤波法:
yn=axn+(1-a)yn-1
(5)
式中,yn是本次滤波输出值;a是滤波系数,其值大于0 小于1;xn是本次采样值;yn-1是上次滤波输出值。
滤波系数a的计算方法:
(6)
式中,fL是截止频率,t是采样时间间隔。
限幅滤波法:
(7)

3拍击振动特性分析
3.1弧长差特性
首先探讨不同侧隙条件下的齿轮拍击振动规律, 选取主动轮转速为同一值120 r/min,即恒速运转。对比分析中心距分别为76.2 mm、76.5 mm、76.8 mm、77.1 mm及77.4 mm 的弧长差特性。


图2 中心距76.2mm下的弧长差曲线Fig.2Arclengthdifferencecurveat76.2mm图3 中心距76.5mm下的弧长差曲线Fig.3Arclengthdifferencecurveat76.5mm图4 中心距76.8mm下的弧长差曲线Fig.4Arclengthdifferencecurveat76.8mm


图5 中心距77.1mm下的弧长差曲线Fig.5Arclengthdifferencecurveat77.1mm图6 中心距77.4mm下的弧长差曲线Fig.6Arclengthdifferencecurveat77.4mm图7 不同中心距下的弧长差对照Fig.7Arclengthdifferencecurvesofdifferentcenterdistances
从图2 可以看出,中心距为76.2 mm 时,弧长差不是恒定值,而是时变的,并且其包络线呈正弦波动趋势。从图2~6 可以看出,不同的齿侧间隙下的主动轮、从动轮的弧长差均具有此特性,即无论拍击是否发生,均有这一固有特性。因此可以推测:齿轮在啮合变形时,相应的变形位移也是时变的,且呈正弦规律。由于篇幅有限,这里不再赘述不同转速条件下弧长差均呈正弦变化规律的对照分析。
针对于图2~6,对弧长差曲线进行正弦波动幅值的特征提取,得到不同侧隙下的弧长差曲线随转速的变化规律,如图7 所示。
从图7 可以看出,五种不同的侧隙条件下,弧长差的波动幅值均随着转速升高出现缩小的趋势。
针对于图2~6,对弧长差曲线进行正弦波动峰值、谷值的特征提取,得到不同侧隙、不同转速下的弧长差曲线的变化规律,如图8~12 所示。


图8 76.2mm下的弧长差峰值、谷值变化Fig.8Arclengthdifference’speak-valleyat76.2mm图9 76.5mm下的弧长差峰值、谷值变化Fig.9Arclengthdifference’speak-valleyat76.5mm图10 76.8mm下的弧长差峰值、谷值变化Fig.10Arclengthdifference’speak-valleyat76.8mm
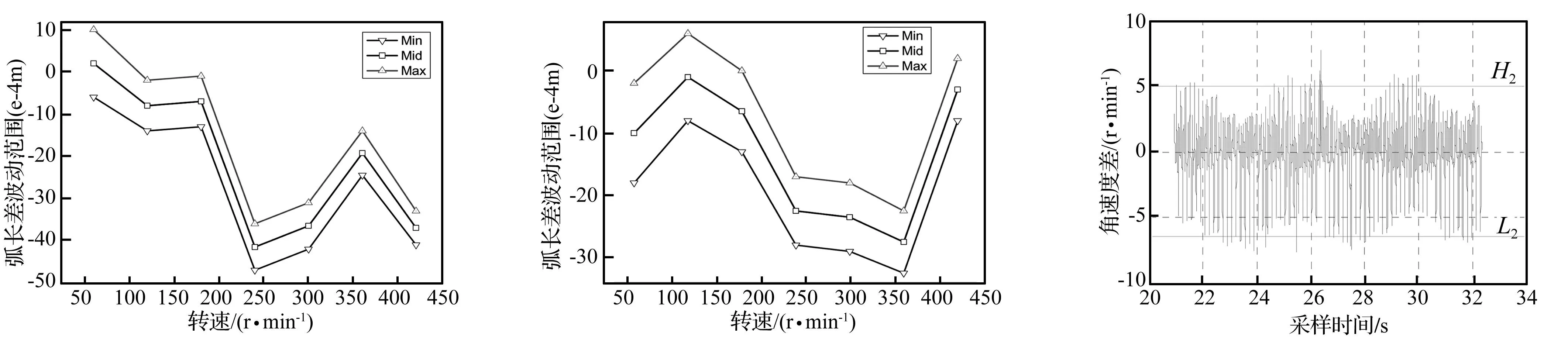

图11 77.1mm下的弧长差峰值、谷值变化Fig.11Arclengthdifference’speak-valleyat77.1mm图12 77.4mm下的弧长差峰值、谷值变化Fig.12Arclengthdifference’speak-valleyat77.4mm图13 某工况下的转速差曲线Fig.13Rotatespeeddifferencecurveunderacertaincondition
从图8~12 可以看出,不同侧隙、不同转速下的弧长差曲线的峰谷值的规律性不明显,即弧长差的中心线位置变化与齿侧间隙、主动轮转速无关,因此可以推测,弧长差的中心线位置仅与齿轮副啮合的初始位置相关。
3.2转速差特性
前一小节系统的分析了主动轮、从动轮的弧长差规律特性,对弧长差做简要处理,可以进一步分析啮合齿轮副的转速差特性。
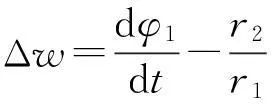
(8)
式中,Δw是转速差;φ1是主动轮转动弧度;φ2是从动轮转动弧度。
以中心距76.2 mm 、主动轮转速360 r/min 工况为实例,采用上述方法处理得到相应的转速差曲线,如图13 所示。
从图13 可以看出,转速差Δw的变化范围是图中线L2和H2之间的距离, 约在-6 r/min~+5 r/min 之间变化,说明齿轮在啮合过程中出现了拍击现象。需要说明的是,此拍击现象虽然发生于恒速360r/min 时,但由于控制精度、润滑等因素影响,齿轮转速必然是波动的,所以才会出现拍击现象。
针对于图13,对转速差曲线进行波动峰值、谷值的特征提取,得到不同侧隙、不同转速下的转速差曲线的变化规律,如图14~图18所示。


图14 76.2mm下的转速差波峰、波谷变化Fig.14Rotatespeeddifference’speak-valleyat76.2mm图15 76.5mm下的转速差波峰、波谷变化Fig.15Rotatespeeddifference’speak-valleyat76.5mm图16 76.8mm下的转速差波峰、波谷变化Fig.16Rotatespeeddifference’speak-valleyat76.8mm
从图14 可以看出,①中心距为76.2 mm时,主动轮转速在240 r/min 后,转速差达到5 r/min 且后续变化很小,因此可以判定中心距76.2 mm 的拍击门槛转速为240 r/min;②当齿轮副参数确定后,发生拍击效应的转速差(5 r/min~6 r/min)也基本确定,并不随转速升高而增大;③在转速较低时,波谷值小于波峰值,在转速较高尤其在拍击门槛转速之后,波谷值大于波峰值。因此可以推断发生拍击时,偏向齿向和齿背的程度不同,即随着转速的升高,拍击具有从齿向往齿背靠近的趋势;④五种不同中心距对应着不同的齿侧间隙,均发生了拍击效应,说明侧隙是产生拍击效应的前提条件。
同理,从图15可以看出,中心距76.5 mm的拍击门槛转速为240 r/min;从图16 可以看出,中心距76.8 mm 的拍击门槛转速为240 r/min;从图17 可以看出,中心距77.1 mm的拍击门槛转速为240 r/min;从图18 可以看出,中心距77.4 mm 的拍击门槛转速为180 r/min。将不同中心距下的拍击门槛转速进行汇总,如图19 所示。


图17 77.1mm下的转速差波峰、波谷变化Fig.17Rotatespeeddifference’speak-valleyat77.1mm图18 77.4mm下的转速差波峰、波谷变化Fig.18Rotatespeeddifference’speak-valleyat77.4mm图19 不同中心距对拍击门槛转速影响Fig.19Thresholdspeedofdifferentcenterdistances
从图19 可以看出,不同侧隙下,所对应的拍击门槛转速不同,而且随着齿侧间隙的增大,拍击门槛转速降低,即更易出现拍击振动现象。
4结论
(1)不同齿侧间隙、不同转速条件下,主动轮、从动轮的弧长差包络线均呈正弦波动趋势。
(2)弧长差的波动幅值均随着转速升高而出现缩小的趋势;弧长差的中心线位置变化与齿侧间隙、主动轮转速无关,仅与齿轮副啮合的初始位置相关。
(3)通过分析不同侧隙下的转速差曲线,可以看出转速差达到5 r/min 后基本恒定,因此该值可作为拍击门槛转速的判定条件。
(4)当齿轮副参数确定后,发生拍击效应的转速差也基本确定,并不随转速升高而增大。
(5)当拍击效应发生时,偏向齿向和齿背的程度不同,即随着转速的升高,拍击具有从齿向往齿背靠近的趋势。
(6)齿侧间隙是产生拍击振动的前提条件,而且随着侧隙的增大,拍击门槛转速降低,更易出现拍击振动现象。
参考文献
[1]Seaman R L, Johnson C E, Hamilton R F. Component inertial effects on transmission design[J]. SAE Techuical Paper Sevies,1984,841686:1-10.
[2]Comparin R J, Singh R. An analytical study of automotive neutral gear rattle[J]. Journal of Mechanical Design,1990, 112(2): 237-245.
[3]Pfeiffer F, Kunert A. Rattling models from deterministic to stochastic processes[J]. Nonlinear Dynamics. 1990, 1(1): 63-74.
[4]Xu K, Deng X Z, Yang J J, et al. Dynamic response analysis for non-smooth gear rattling system[C]. IEEE, 2009.
[5]GAO Zhi-ying,DONG Hai-jun, SHEN Yun-wen. Bifurcation character of rattling in the gear system under the excitation of the rotational speed fluctuation[J]. Chinese Journal of Mechanical Engineering, 2006,42(2):168-172.
[6]Brancati R, Rocca E, Russo R. An analysis of the automotive driveline dynamic behaviour focusing on the influence of the oil squeeze effect on the idle rattle phenomenon[J]. Journal of Sound and Vibration,2007, 303(3): 858-872.
[7]Ottewill J R, Neild S A, Wilson R E. An investigation into the effect of tooth profile errors on gear rattle[J]. Journal of Sound and Vibration, 2010, 329(17): 3495-3506.
[8]Barthod M, Hayne B, Tébec J L, et al. Experimental study of dynamic and noise produced by a gearing excited by a multi-harmonic excitation[J]. Applied Acoustics, 2007, 68(9): 982-1002.
[9]Barthod M, Hayne B, Tébec J L, et al. Experimental study of gear rattle excited by a multi-harmonic excitation[J]. Applied Acoustics,2007, 68(9): 1003-1025.
[10]Theodossiades S, Tangasawi O, Rahnejat H. Gear teeth impacts in hydrodynamic conjunctions promoting idle gear rattle[J]. Journal of sound and vibration,2007, 303(3): 632-658.
[11]Rocca E, Russo R. Theoretical and experimental investigation into the influence of the periodic backlash fluctuations on the gear rattle[J]. Journal of Sound and Vibration, 2011, 330(20):4738-4752.
[12]Ottewill J R, Neild S A, Wilson R E.Intermittent gear rattle due to interactions between forcing and manufacturing errors[J]. journal of Sound and Vibration, 2009, 321(3): 913-935.

