基于最小位移的磁悬浮转子变极性LMS反馈不平衡补偿

第一作者宋腾男，硕士生，1990年12月生

通信作者韩邦成男，博士，研究员，1974年生

基于最小位移的磁悬浮转子变极性LMS反馈不平衡补偿

宋腾1,2，韩邦成1,2，郑世强1,2，冯锐1,2

(1.北京航空航天大学惯性技术重点实验室，北京100191；2.北京航空航天大学新型惯性仪表与导航系统技术国防重点学科实验室，北京100191)

摘要：针对高速电机磁悬浮转子受不平衡扰动时位移精度下降的问题，提出一种基于最小位移原则的变极性最小均方误差(least mean square，LMS)反馈不平衡补偿策略，通过在线辨识位移信号中的转速同频分量，引入反馈补偿来增加系统对同频分量的广义动刚度，实现不平衡补偿。利用广义根轨迹分析了引入补偿后系统的闭环稳定性，同时针对仅以负极性或正极性引入补偿后，闭环系统均存在临界转频以上或以下发散的问题，设计了通过切换引入补偿的极性来穿越临界转频，从而实现引入LMS反馈补偿后全转速范围闭环稳定。实验结果表明，该方法在全转速范围内均能大幅减小位移信号中的转速同频分量。

关键词：主动磁悬浮轴承；最小位移；不平衡补偿；变极性LMS反馈；广义根轨迹

基金项目：航空创新基金(2012Z1315)；国家自然科学基金资助项目(61203203)；国家重大科学仪器设备开发专项(2012YQ040235)；北京市科技创新基地培育与发展工程专项项目(J131104002813105)

收稿日期：2014-01-28修改稿收到日期：2014-04-10

中图分类号:TP273

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.004

Abstract:In consideration of the decrease of high-speed motor magnetic rotor displacement accuracy generated by unbalance vibration, a LMS feedback algorithm based on the principle of displacement nulling was proposed. The generalized dynamic stiffness of the system was improved by online identifying the same-frequency component in displacment signal and adding feedback to achieve unbalance compensation. In addition, the stability of close loop system was analyzed by use of generalized root locus; meanwhile, to cross over the critical frequency and achieve the displacement compensation within the whole speed range, a variable polarity strategy was raised. The experiment results demonstrate the method can suppress the displacement same-frequency vibration effectively within the whole speed range.

Variable polarity LMS feedback based on displacement nulling to compensate unbalance of magnetic bearing

SONGTeng1,2,HANBang-cheng1,2,ZHENGShi-qiang1,2,FENGRui1,2(1.Science and Technology on Inertial Laboratory (Beihang University), Haidian District, Beijing 100191, China;2.Fundamental Science on Novel Inertial Instrument & Navigation System Technology Laboratory (Beihang University), Haidian District, Beijing 100191, China)

Key words:active magnetic bearing; displacement nulling; unbalance compensation; variable polarity LMS feedback; generalized root locus

相较于传统机械轴承，磁悬浮轴承具有无磨损、无需润滑、可在线监控、可实施主动振动控制等优点，在工业部门、航空航天[1-2]等领域的应用日益普遍。对于转子而言，由于机械加工误差、材料的质量在几何分布上不均匀等原因，必然存在惯性轴、几何轴以及旋转轴三者不重合的问题，将会导致转子产生不平衡振动。而转子不平衡激振力的大小与转速的平方成正比，随着转速升高，急剧增加的激振力会严重影响转子系统的稳定运行[3]。因此，采取有效措施对高速转子进行主动振动控制就显得尤为必要。

磁悬浮转子主动振动控制的方法主要分为两大类。一类称之为自动平衡，其基本思想是在反馈通道中通过消除位移传感器输出信号中的转速同频分量，减小控制器的同频信号输出，从而有效地降低磁轴承线圈中的同频控制电流以及相应的电流刚度力，利用转子在高速旋转时的自对中效应使其围绕惯性轴旋转。这类控制策略按照“零控制电流”的原则进行，其典型方法包括自适应广义陷波器法[4-5]、迭代学习控制法[6-7]、自调谐模糊PID法[8]、等效干扰电压矢量补偿法[9]、迭代搜索算法[10]、Q-parameterization法[11]、自适应LMS滤波法[12]，等。自动平衡法虽然可以有效减小通过径向磁轴承传递给基础的转速同频反作用力[9,12]，但是它无法抑制转子位移信号中的转速同频涡动，不能满足对转子位移精度要求高的场合，如机床主轴电机等的应用要求。另一类方法则可称之为不平衡补偿，其基本思想是通过提高系统对转子位移信号的广义动刚度，增加控制器输出，使得线圈产生额外的补偿电磁力来抵消不平衡激振力，最终实现抑制转子位移的同频振动、使其围绕几何轴旋转的目的。这类控制策略按照“零转子位移”的原则进行，蒋科坚[13]等提出一种基于振动识别的补偿方法，它虽然能够通过检测位移响应中不平衡振动的幅值和相位变化，产生精确的补偿电磁力，但是其计算量大、算法复杂，对硬件平台要求高；龙亚文等[14]采用混合灵敏度H∞控制策略设计鲁棒控制器，实现磁悬浮转子的振动抑制；Tian 等[15]运用离散时间滑模变结构控制实现最小位移补偿，该方法虽然鲁棒性较强，但是参数不易整定，补偿精度不高；Shi等[16-17]提出运用自适应滤波xLMS算法实现磁悬浮转子最小位移补偿，该方法虽然补偿精度高且实现简单，但是文献[16]中仅在固定转速(1300r/min)对其进行了实验验证，不仅试验中所设转速偏低，而且未进一步探讨自适应滤波xLMS算法取不同的中心频率时对闭环系统稳定性的影响。而事实上，滤波中心频率应与转频保持一致才能实现有效的补偿，且随着转速升高，单纯以负反馈形式引入不平衡补偿会使闭环系统的特征多项式出现右半平面极点，造成系统失稳。

文献[18-19]将LMS算法运用于磁悬浮隔振器的振动主动控制。本文在位移最小原则的不平衡补偿策略基础上，提出利用自适应LMS算法在线实时辨识转子位移信号中的转速同频分量，将辨识量反馈至位移参考信号处来增加系统对位移同频分量的广义动刚度，达到对位移信号中的同频分量进行抑制的目的。并且结合系统模型，利用广义根轨迹分析插入自适应LMS算法后系统的稳定性，得出系统临界稳定转频，据此设计出变极性反馈策略，从而保证在全转速范围内系统闭环的稳定，且同频位移最小。在高速永磁偏置磁轴承4 kW电机上测得的实验结果证明了该方法的有效性。

1不平衡转子动力学分析

经典的磁悬浮轴承电磁力公式[20]经线性化后为(以A端X通道为例)：

FAX=kiiAX+kxxA

(1)

式中，FAX为转子所受单通道电磁力，ki为电流刚度，kx为位移刚度。图1为主动磁轴承系统径向四通道的受力分析。将空间直角坐标系OgXYZ的原点设于转子质心处。

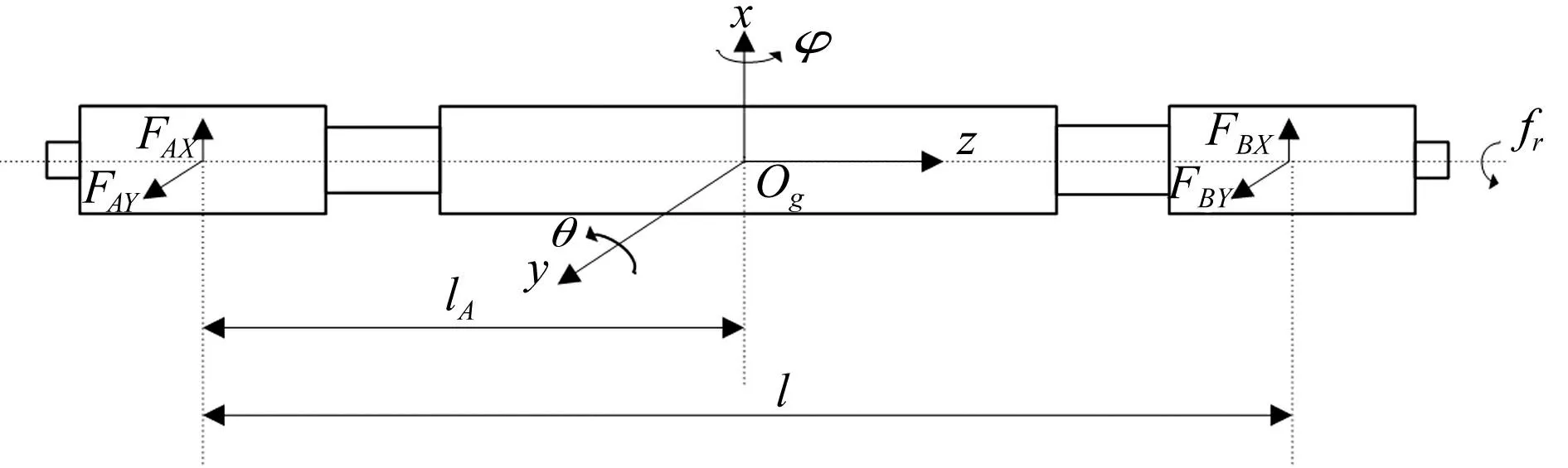
图1　转子径向受力分析 Fig.1 Force analysis of rotor in radial direction

图1中，FAX、FAY、FBX、FBY分别为转子在A、B两端所受沿x方向、y方向的电磁力；φ、θ分别为绕x轴、y轴旋转的角位移，ωr为转频。则可得转子动力学方程如下：

(2)

其中Ir为转子的赤道转动惯量，Ia为极转动惯量；fx、fy为不平衡激振力在x轴、y轴上的分量。

(3)

其中e1为旋转中心Or与质心Og之间的距离，ψ为形心——质心连线与旋转坐标系ζOrη横轴之间的夹角。转子几何中心Oc的位移与A、B两端处位移关系为[21]：

(4)

图2　转子截面示意图 Fig.2 Schematic diagram of rotor section

图2为考虑不平衡振动时的转子截面示意图，其中ep=|OcOg|为转子偏心距。

可得转子形心与质心之间的坐标变换关系如下：

(5)

考虑到径向四通道电磁力具有各向同性，结合式(2)~(5)可得矩阵形式的径向四自由度运动学微分方程如下：

(6)

式中，fx′、fy′是磁轴承相应的不平衡外扰力在x轴、y轴上的分量，其表达式如下：

(7)

由式(7)可知，当转子形心与质心重合时，ep=e1，外扰力为零。式(6)可简化表示为：

(8)

式中，X = (xAxByAyB)T，ic= (iXAiXBiYAiYB)T，f ′= (fx′fy′00)T；M为质量阵，C为阻尼阵，Kx为位移刚度阵，Ki为电流刚度阵，E为扰动响应阵。设位移传感器电压位移系数为ks，则有传感器位移信号转换矩阵Ks：

(9)

对于一般意义上的磁轴承闭环反馈控制系统，从控制电流到位移的转换关系为：

X(s)=-Amp(s)Gc(s)Ksic(s)

(10)

其中，X(s)、ic(s)分别为X、ic经拉普拉斯变换后的表达形式；Gc(s)为控制器传递函数，Amp(s)为功率放大环节传递函数。则有：

(11)

取s=jw，可得其频率特性关系：

X=-Amp(jw)Gc(jw)Ksic

(12)

将式(12)代入式(8)并移相得：

Ef′

(13)

令K′=KiAmp(jw)Gc(jw)Ks-Kx，则(13)式可变形为：

(14)

由式(14)可知，此时系统具有在简谐外力作用下的受迫振动特性[21]，K′为磁轴承系统的广义动刚度，化简可得：

(15)

X(t)=e-ζwnt (a1coswdt+a2sinwdt)I+

Bdsin(wrt+ψd)I

(16)

(17)

由式(17)可知，欲抑制转子的受迫振动，应设法提升系统广义动刚度K′。由其表达式可知，Kx、Ki、Ks均为定值，功放环节频率特性亦为系统本身属性。因此广义动刚度的大小基本取决于控制器的频率特性。一般而言，仅仅通过调节PID控制器参数来增加系统广义动刚度显然难以满足需求[21]，所以应当在控制器中引入对位移信号中同频分量的额外补偿，大幅增加系统对同频信号的广义动刚度，方可有效地实现最小位移补偿。

2运用变极性LMS反馈实施最小位移控制

2.1引入LMS反馈增加系统广义动刚度

对于高速磁悬浮电机而言，由于其转子轴为细长型，赤道转动惯量Ir远远大于极转动惯量Ia，故可忽略陀螺效应，将前文中描述的多输入多输出(MIMO)系统分别视为独立解耦的单输入单输出(SISO)系统。下文中，以B端磁轴承x通道为例进行论述。

式(16)为仅考虑系统固有自由振动和转速同频不平衡振动的转子位移信号时域表达式。但事实上，由于转子所受多种外界扰动力，再加上定子与转子之间气隙空间的磁通密度分布并非严格对称，故而转子位移信号中实际包含的频谱分量很丰富。只是由于在所有外界扰动力中同频振动占据主导地位，因此同频分量的权重最大。为了实现不平衡补偿，首先要实时辨识出位移信号中的同频分量。辨识方法如图3所示。

图3　位移信号同频分量辨识 Fig.3 Identifying the same-frequency component of displace signal

其具体算法流程如下：

v(kT)=w1(kT)sin(wrkT)+w2(kT)cos(wrkT)

(18)

w1((k+1)T)=w1(kT)+2μx(kT)sin(wrkT)

(19)

w2((k+1)T)=w2(kT)+2μx(kT)cos(wrkT)

(20)

式中，x(kT)为位移信号，w1(kT)、w2(kT)分别为转速同频正余弦分量的权重系数，v(kT)为输出信号，μ为权重系数迭代变化步长，T为系统采样周期。由文献[22]可知，对此环节进行Z变换后，其脉冲传递函数如下：

(21)

步长μ应当满足条件：0 <μ< 1/λmax，方能满足稳定收敛[10]。将V(z)以负反馈形式引致闭环系统参考位移处后，可得磁轴承控制系统结构如图4所示。

此时，系统广义反馈环节的脉冲传递函数为：

H′(z)=1+H(z)=

(22)

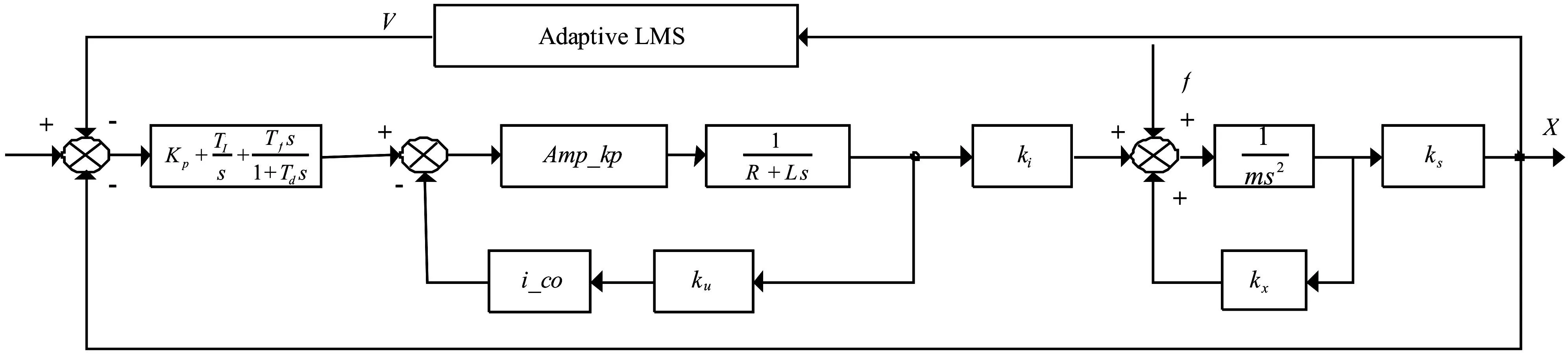
图4　磁轴承控制系统结构框图 Fig.4 Scheme of magnetic bearing control system

因为z=ejwT，故当w=wr时，有zr为H′(z)极点。根据H′(z)的频率特性，显然有：

H′(jwr)≫H′(jw)(w≠wr)≈1

(23)

前面已论述过可将磁轴承系统视为分别独立解耦的SISO系统，故广义刚度矩阵K″近似可视为对角阵，即K″=diag{k″,k″,k″,k″}，其中k″为单通道广义刚度系数。则引入LMS反馈之后，单通道广义刚度系数变为：

(24)

故有k″(jwr)≫k′(jwr)，根据前文分析，此时本通道转子位移信号中的同频分量已得到有效减小。

2.2利用广义根轨迹分析系统闭环稳定性

判断一种控制算法是否切实可行，不仅应衡量其是否能有效地解决所针对的特定问题，还应着重考察将这种算法加入原系统之后，对整个系统性能所造成的影响。对控制系统而言，保证系统稳定是其正常运行首当其冲的必要条件。前文已经论述了引入LMS反馈后能够实现对转子所受不平衡激振力的有效补偿，接下来本节将应用广义根轨迹的方法分析其闭环稳定性。

考察图(4)所示磁轴承控制系统，PID控制器传递函数为：

(25)

功率放大环节传递函数为：

(26)

电磁力——转子环节传递函数为：

(27)

再加上式(22)所示引入LMS广义反馈环节脉冲传递函数，故整个闭环系统应为7阶系统，以转频fr为变量绘制其广义根轨迹，其中有三条始终分布于左半实轴上且距离虚轴较远，另外两条始终位于左半平面且远离虚轴，只有两条位于虚轴附近，故为系统的主导根轨迹，其分布图如图5所示。

图5　引入负极性LMS反馈后闭环系统主导根轨迹 Fig.5 The major root locus of close loop system while adding negative LMS feedback

由图5可知，随着转频fr升高，两条主导根轨迹会由左半平面穿越虚轴进入右半平面，此时系统闭环发散。穿越虚轴时所对应的临界转频fc= 126 Hz。可见，单纯地以负极性形式引入LMS反馈补偿，无法在临界转频以上的转速实现不平衡补偿。

2.3通过切换反馈极性穿越临界转频

当以正极性引入LMS反馈补偿之后，系统闭环反馈环节传递函数变为：

H′(z)=1-H(z)=

(28)

图6　(a) 负、正极性LMS反馈系统主导根轨迹 Fig.6(a) The major root locus of system while adding positive and negative LMS feedback

图6　(b) 引入极性切换策略后系统主导根轨迹分布图 Fig.6 (b) The major root locus of system while introducing polarity switch strategy

由图6(a)可见，正、负极性LMS反馈引入系统后的主导根轨迹分布在S域内关于虚轴对称。当fr>fc时，正极性LMS反馈系统的闭环极点全部位于S域左半平面，此时系统闭环稳定。为了解决2.2中所提出的问题，不妨通过极性切换的手段穿越临界转频，其具体策略如图7所示。

图6(b)为引入极性切换的系统主导根轨迹分布图。可见，此时系统闭环主导极点均位于S域左半平面，故系统在全转速范围内闭环稳定。

图7　全转速范围极性切换LMS反馈补偿策略 Fig.7 The strategy of polarity switch LMS feedback among the whole speed range

图8为μ取不同值时的主导根轨迹分布情况，为了便于说明，取负极性LMS反馈补偿。可见，随着转频fr升高，三者的系统主导极点位置变化具有相同的趋势，并在同一点穿越虚轴进入S域右半平面，而且三者对应的临界转频也完全一致，故可说明μ的取值对系统的稳定性没有影响。但是也可以看出，在相同的fr条件下，当μ的取值越大，系统的根轨迹实部越远离虚轴，所以系统的响应时间越短。

图8　μ取不同值时系统主导根轨迹 Fig.8 The major root locus of system in different μ

3仿真分析

磁悬浮转子不平衡补偿的实质是引入与不平衡激振力大小相同、相位差180°的电磁力补偿，使得径向每个通道转子所受合力尽可能接近于零，从而保证转子沿几何轴旋转。事实上，由式(24)可知，转子所受电磁力中的电流刚度力远远大于位移刚度力，故可近似认为电磁力约等于电流刚度力。为了验证引入LMS反馈之后的不平衡激振力补偿效果，根据在实验中实际设置的控制器参数(表1)和实际的广义被控对象参数(功放环节+4kW电机永磁偏置磁轴承、表2)，通过Matlab进行仿真分析。

表1　实验中磁轴承控制系统实际参数

图9 (a)转子所受合外力时间关系曲线Fig.9(a)Thecurveofthecombinedforceoftherotor图9 (b)单纯PID时转子受力时间关系曲线Fig.9(b)ThecurveofrotorforcewhilepurelyPID图9 (c)引入LMS反馈补偿后转子受力时间关系曲线Fig.9(c)ThecurveofrotorforcewhileaddingLMSfeedbackcompensation

表2　广义被控对象参数

在仿真分析中，加入的不平衡激振力为：f=500sin(2πfrt)，其中fr= 100 Hz。图9(a)为转子所受合力时间关系曲线图，在0.25 s时加入补偿，转子所受合力在短时间内收敛至零。如图9(b)所示，未引入LMS反馈补偿时，转子所受电流刚度力与不平衡激振力之间存在介于0°与180°之间的相位差，不仅无法实现不平衡补偿，反而会使转子有离心趋势；如图9(c)所示，引入LMS反馈补偿后，电流刚度力能够几乎抵消不平衡激振力，使得转子所受合力基本为零，从而实现了对不平衡激振力的完全补偿。

4实验验证

利用北航研制的高速永磁偏置磁轴承4 kW电机，对变极性LMS反馈实现不平衡补偿进行实验验证，其主要技术参数如表2所示。磁轴承控制系统采用TMS320F28335+FPGA数字控制系统，根据转子位移信号，计算控制量，生成PWM波形，驱动功率放大环节产生控制电流，从而保证磁悬浮转子的稳定悬浮。

由于系统引入的自适应LMS反馈环节需要转子转频的实时信息，故利用霍尔传感器检测电机转速，再经DSP的ECAP模块捕获后进行处理，来实时计算转子转频。

LMS算法的权重系数w1、w2的迭代更新步长μ是影响算法收敛速度的关键参数。如图10，试验中转频为150 Hz(9 000 r/min)时，分别取步长μ=0.000 05，0.000 5，0.005，引入LMS反馈之后位移信号均收敛。显然，三者收敛后的峰峰值十分接近；但是当μ=0.000 05时，收敛时间ts=2.715 s，当μ=0.000 5，收敛时间ts=0.695 s，当μ=0.005时，收敛时间ts=0.999 8 s。此外，当μ取0.000 5时，引入LMS反馈之后可以看出位移信号有一个明显的超调过程。

为了兼顾引入LMS反馈之后的稳定性以及过渡过程的平稳性、快速性，在实际的实验过程中，取步长μ=0.000 5。

当fr在临界转频fc以下时，将LMS反馈量以负极性形式给定参考位移信号处。试验中转频为50 Hz(3 000 r/min)，以B端x通道为例，从图11中可以看到，位移信号振动幅值下降明显；对转子位移信号进行快速傅里叶变换，如图12所示，单纯的PID控制同频分量为-66.89 dB，加入算法后同频分量为-86.74 dB，显然此时位移同频振动已明显衰减。

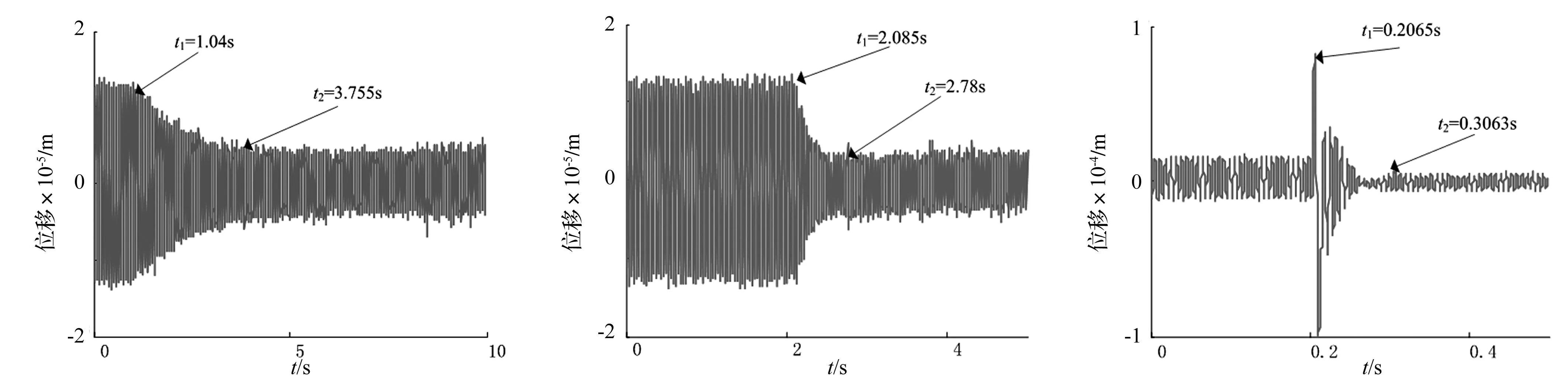
图10 (a)μ=0.00005时位移收敛过程时间关系曲线Fig.10(a)Thecurseofdisplaceconvergencewhenμ=0.00005图10 (b)μ=0.0005时位移收敛过程时间关系曲线Fig.10(b)Thecurseofdisplaceconvergencewhenμ=0.0005图10 (c)μ=0.005时位移收敛过程时间关系曲线Fig.10(c)Thecurseofdisplaceconvergencewhenμ=0.005

图11 fr=50Hz时B通道x方向位移信号时间曲线Fig.11ThecurseofdisplacesignalinthexdirectionofchannelBatfr=50Hz图12 (a)fr=50Hz时单纯PID控制位移信号频谱Fig.12(a)Thefrequencyspectrumofdisplacesignalatfr=50HzwhilepurelyPID图12 (b)fr=50Hz时引入负极性LMS反馈位移信号频谱Fig.12(b)Thefrequencyspectrumofdisplacesignalatfr=50HzwhileaddingnegativeLMSfeedback

当fr在临界转频fc之上时，将LMS反馈量以正极性形式给定参考位移信号处。试验中转频分别取150 Hz(9 000 r/min)和200 Hz(12 000 r/min)，以B端x通道为例，从图13、15中可以看到，位移信号振动幅值下降明显；对转子位移信号进行快速傅里叶变换，如图14所示，转频为150 Hz时，单纯的PID控制同频分量分别为-67.6 dB，加入算法后下降至-86.39 dB；如图16所示，转频为200 Hz时，单纯的PID控制同频分量分别为-72.79 dB，加入算法后下降至-102 dB；显然位移同频振动均已明显衰减。

图13 fr=150Hz时B通道x方向位移信号时间曲线图Fig.13ThecurseofdisplacesignalinthexdirectionofchannelBatfr=150Hz图14 (a)fr=150Hz时单纯PID控制位移信号频谱Fig.14(a)Thefrequencyspectrumofdisplacesignalatfr=150HzwhilepurelyPID图14 (b)fr=150Hz时引入正极性LMS反馈位移信号频谱Fig.14(b)Thefrequencyspectrumofdisplacesignalatfr=150HzwhileaddingpositiveLMSfeedback

图15 fr=200Hz时B通道x方向位移信号时间曲线图Fig.15ThecurseofdisplacesignalinthexdirectionofchannelBatfr=200Hz图16 (a)fr=200Hz时单纯PID控制位移信号频谱Fig.16(a)Thefrequencyspectrumofdisplacesignalatfr=200HzwhilepurelyPID图16 (b)fr=200Hz时引入正极性LMS反馈位移信号频谱Fig.16(b)Thefrequencyspectrumofdisplacesignalatfr=200HzwhileaddingpositiveLMSfeedback

5结论

针对磁悬浮转子的不平衡振动问题，建立了在不平衡激振力作用下的转子动力学模型，通过引入自适应LMS反馈补偿，大幅增加了系统对位移信号中转速同频分量的广义动刚度；利用广义根轨迹的方法分析了加入算法后系统的闭环稳定性问题，指出单一地以负极性或者正极性形式引入LMS反馈补偿均存在系统在临界转频之上或者之下发散的问题。为此，专门设计了变极性反馈的控制策略。仿真和实验均表明，该方法可在保证系统闭环稳定的前提下，实现全转速范围内的最小位移控制。

由于转子所受不平衡激振力与其转速平方成正比，故在转频很高时实施不平衡补偿，需要功放环节提供很大的控制电流。但是，功放环节会在高频时呈现明显的饱和特性，从而给系统带来严重非线性。因此，如何解决实现不平衡补偿需要增加控制电流与功放高频饱和这一对矛盾，有待于进一步深入研究。

参考文献

[1]郑世强，房建成，韩邦成. 提高双框架磁悬浮CMG动态响应能力的磁轴承补偿控制方法与实验研究[J]. 机械工程学报，2010，46(24)：22-28.

ZHENG Shi-qiang，FANG Jian-cheng，HAN Bang-cheng.Compensation control method and experimental study of magnetic bearing to improve dynamic response ability of double gimbal magnetically suspended control moment gyroscope[J]. Journal of Mechanical Engineering，2010，46(24)：22-28.

[2]Shiqiang Zheng，Bancheng Han. Investigations of an integrated angular velocity measurement and attitude control system for spacecraft using magnetically suspended double-gimbal CMGs[J]. Advances in Space Research，2013，51(12)：2216-2228.

[3]刘彬，房建成，刘刚，等. 磁悬浮飞轮不平衡振动控制方法与试验研究[J].机械工程学报，2010，46(12)：188-194.

LIU Bin，FANG Jian-cheng，LIU Gang，et al. Unbalance vibration control and experiment research of magnetically suspended flywheels[J]. Journal of Mechanical Engineering，2010，46(12)：188-194.

[4]Herzog R，Buhter P，Gahler C，et al. Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings [J]. IEEE Transactions on Control Systems Technology，1996，4(5)：580-586.

[5]孙岩桦，罗岷，虞烈. 基于自适应陷波器的电磁轴承不平衡补偿方法[J].振动工程学报，2000，13(4)：610-614.

SUN Yan-hua，LUO Min，YU Lie. UnBalance compensation based on adaptive notch filter to active magnetic bearings[J]. Journal of Vibration Engineering，2000，13(4)：610-614.

[6]BI Chao，WU De-zheng，JIANG Quan. Automatic learning control for unbalance compensation in active magnetic bearings[J].IEEE Transactions on Magnetics，2005，41(7)：2270-2280.

[7]BI Chao，WU De-zheng，JIANG Quan，et al. Optimize control current in magnetic bearings using automatic learning control[C]. Proceedings of IEEE International Conference on Mechatronics，Istanbul，Turkey，2004：305-310.

[8]Chen K Y，Tung P C，Tsai M T，et al. A self-tuning fuzzy PID-type controller design for unbalance compensation in an active magnetic bearing[J]. Expert Systems with Applications，2009，36[4]：8560-8570.

[9]黄晓蔚，唐钟麟. 电磁轴承系统实现自动平衡的一种新方法[J].机械工程学报，2001，37(7)：96-99.

HUANG Xiao-wei，TANG Zhong-lin. New method for autobalancing with active magnetic bearings[J]. Chinese Journal of Mechanical Engineering，2001，7(7)：96-99.

[10]Markert R，Skricka N，Zhang X. Unbalance compensation on fexible rotors by magnetic bearings using transfer functions[C]. 8th International Symposium on Magnetic Bearings，Mito，Japan，2002：417-422.

[11]Mohamed A M，Busch-Vishniac I. Imbalance compensation and automatic balancing in magnetic bearing systems using the Q-Parameterization theory[C]//Proceedings of the American Control Conference，1994，Baltimore，Maryland:2952-2957.

[12]高辉，徐龙祥. 基于LMS 算法的磁悬浮轴承系统振动补偿[J]. 振动工程学报，2009，22(6)：583-588.

GAO Hui，XU Long-xiang. Real-time vibration compensation for active magnetic bearing systems based on LMS algorithm[J]. Journal of Vibration Engineering，2009，22(6)：583-588.

[13]蒋科坚，祝长生. 主动电磁轴承转子系统自适应不平衡补偿控制[J].浙江大学学报(工学版),2011，45(3)：503-509.

JIANG Ke-jian，ZHU Chang-sheng. Adaptive unbalance compensation control of active magnetic bearing supporting rotor system[J]. Journal of Zhejiang University(Engineering Science)，2011，45(3)：503-509.

[14]龙亚文，谢振宇，徐欣. 磁悬浮轴承H鲁棒控制策略研究[J].振动与冲击,2013,32(23):115-120.

LONG Ya-wen, XIE Zhen-yu,XU Xin. H∞robust control strategy for an active magnetic bearing[J].Journal of Vibration and Shock,2013,32(23):115-120.

[15]Tian H，Nonami K. Discrete-time sliding mode control of flexible rotor-magnetic bearing systems[J]. International Journal of Robust and Nonlinear Control，1996，6(7)：609-632.

[16]Shi J，Zmood R，Qin L J. The direct method for adaptive feed-forward vibration control in magnetic bearing systems[C]. Proceedings of the seventh International Conference on Control，Automation，Robotics and Vision，2002，Singapore：675-680.

[17]Shi J，Zmood R，Qin L J. The indirect adaptive feed-forward control in magnetic bearing systems for minimizing selected vibration performance measures[C]. 8th International Symposium on Magnetic Bearing，2002，Mito，Japan：223-228.

[18]魏璀璨，王永，陈绍青，等. 磁悬浮隔振器分块归一化LMS算法控制研究[J]. 振动与冲击，2012，31(18)：100-103.

WEI Can-yong，WANG Yong，CHEN Shao-qing，et al. Control of an electromagnetic suspension vibration isolator based on block normalized LMS algorithm[J]. Journal of Vibration and shock，2012，31(18)：100-103.

[19]陈昊，王永，李嘉全，等. 基于饱和约束LMS算法的磁悬浮隔振器控制研究[J]. 振动与冲击，2012，31(18)：125-128.

CHEN Hao，WANG Yong，LI Jia-quan，et al. Control of an electromagnetic suspension vibration isolator based on LMS algorithm with saturation constraint[J]. Journal of Vibration and Shock，2012，31(18)：125-128.

[20]Schweitzer G，Maslen E H. Magnetic bearings：theory，design，and application to rotating machinery[M]. New York：Springer，2009：55-105.

[21]高辉.主动磁悬浮轴承系统不平衡振动补偿研究[D].南京：南京航空航天大学，2011.

[22]沈福民.自适应信号处理[M].西安,西安电子科技大学出版社，2001：48-50.