基于OptiStruct的襟翼摇臂的拓扑优化

郭仕贤

【摘 要】本文通过拓扑优化的方法，采用Altair公司的OptiStruct软件对襟翼摇臂进行优化，在满足其使用刚度、强度要求的情况下，实现减重32.9%。

【关键词】拓扑优化；减重；OptiStruct

0 引言

飞机结构设计中，减重是一个永恒的难题。“为了减轻飞机每一克重量而奋斗”是每一个飞机设计师的格言。因此，进行结构减重，优化势在必行。减重就意味着飞机的油耗小，成本低，更环保节能，可以减少二氧化碳的排放，才能更有竞争力。

1 拓扑优化理论基础

结构拓扑优化能在工程结构设计的初始阶段为设计者提供一个概念性设计，使结构在布局上能够采用最优方案，已经成为当今研究结构优化设计的一个热点。OptiStruct是一个面向产品设计、分析和优化的有限元和结构优化求解器，拥有先进的优化技术，提供全面的优化方法。变密度法是连续体拓扑优化的常用方法，是一种比较流行的力学建模方式，与采用尺寸变量相比，它更能反应拓扑优化的本质特征。它也正是OptiStruct中所采用的材料插值方法。变密度法的基本思想是引入0到1的可变材料，指定每个有限单元的密度相同，并以每个单元的相对密度为设计变量。当单元相对密度t=0时，表示该单元无材料，单元应删除；当单元相对密度t=l时，表示该单元有材料，保留或增加该单元。

其中， C（x）为结构的总体柔度，F为为力向量，U为为位移阵列，K为为结构总体刚度矩阵，V0——为整个设计域的初始体积，F为优化体积比，V是结构优化后的结构体积，Ve为优化后的单元体积，X为设计变量，Xe为单元设计变量，Xmax为单元设计变量上限，Xmin为单元设计变量下限，引入密度Xmin下限的目的是防止单元刚度矩阵奇异，p为惩罚因子，N为结构离散单元总数。

2 摇臂结构的介绍

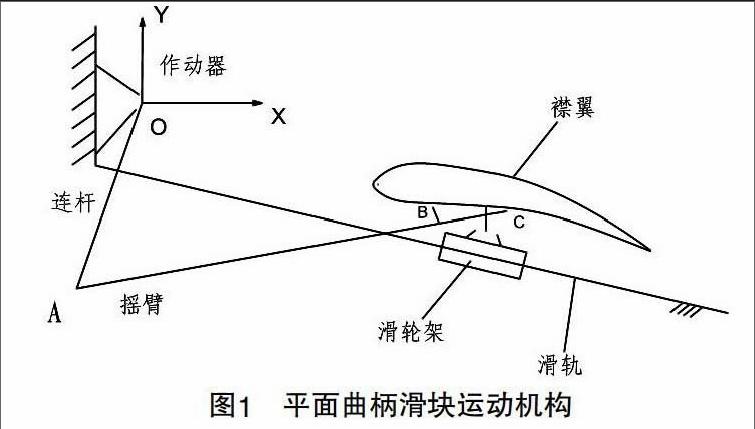
目前，大型飞机后缘襟翼运动机构普遍都是采用滑轨引导襟翼的形式。滑轨限定襟翼的运动轨迹，襟翼与滑轨之间通过滑轮架连接，作动器的动力通过驱动连杆及摇臂的传递，使襟翼沿滑轨平动并转动。示意图见图1，摇臂结构见图2。其中，B、C两点与襟翼本体采用球铰连接，A点与作动器连杆采用球铰连接。

3 有限元模型的建立

3.1 模型前处理

为了对襟翼摇臂优化前的结构进行强度分析，需对模型进行适当的简化及网格划分。使用Hypermesh强大的几何清理功能对导入的CAD模型进行几何清理，网格划分结构如图3所示：

3.2 结构材料性能

襟翼摇臂所使用的材料为7050-T7451，材料参数如表1所示：

3.3 载荷与边界条件

由于B、C点与襟翼本体为球绞连接，因此在B和C点约束x，y和z方向的位移，以摇臂在整个飞行过程中的最严重工况，在A点上进行加载，作用力大小为Fx=5836N，Fy=16701N。采用此约束条件进行计算时会发现，由于两个球铰无法约束其绕两个球铰连线的转动，因此会出现位移的错误。因此，需要增加一个约束条件，限制加载点在z方向的位移。

对摇臂进行分析，得出其最大变形发生在A点位置，大小为10.36mm。

3.4 优化模型的建立与优化

设计空间与非设计空间：非设计空间主要是在优化中不参与优化的空间，主要是由该结构件与其他结构的接口所决定，考虑到连接点A、B和C与其他结构连接接口需要保留，因此将其连接耳片区域作为非设计区域，如图4黄色部分，而将其他部分作为设计区域，并将其中结构填实。根据结构的受力情况，摇臂主要承受弯矩，因此增加结构高度能够有效的增加抗弯能力，结合该结构的运动空间，更改后的设计区域如图5蓝色部分。

以襟翼摇臂的最大变形量10.36mm作为约束条件，以最小化总体积作为目标函数，在Hypermesh中建立拓扑优化模型。同时在优化中采用了对称约束和拔模方向约束，以保证摇臂结构的对称和优化结构的可加工性。

4 优化结构

使用Optistruct优化设计工具求解得到基于变密度法的优化结果如图6所示：

考虑到腹板在本结构中的作用，在重建CAD模型时，保留了2mm的腹板厚度。根据拓扑优化的结果及实际设计中对加工性能的要求，对襟翼摇臂重新建立CAD以及有限元模型，把优化后的有限元模型提交Radioss进行分析和结果的后处理，其最大变形量和最大应力如表2所示：

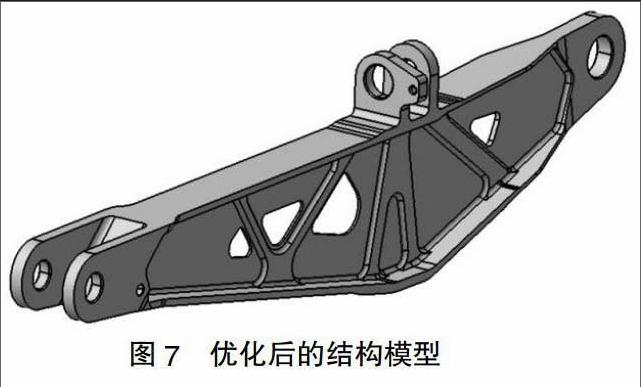
从表2中可以看出，与优化前相比，优化后的摇臂质量下降了32.9%，位移基本保持不变，最大应力增加4MPa，在材料的许用强度之内。对重建的CAD模型进行有限元分析，并对其中的应力集中处进行适当的增厚与倒圆角。优化后模型如图7所示：

5 结论

通过Optistruct 拓扑优化，在不减少零件刚度增加零件最大应力情况下，零件重量由原来的2.412kg减少为1.618kg，实现了减重32.9%。

【参考文献】

[1]Altair Engineering Inc.HyperWorks Users Manual Version 11.0.

[2]于开平，周传月，等.Hyper Mesh 从入门到精通[M].科学出版社，2005.

[3]李楚琳，张胜兰，等.HyperWorks 分析应用实例[M].机械工业出版社，2008.