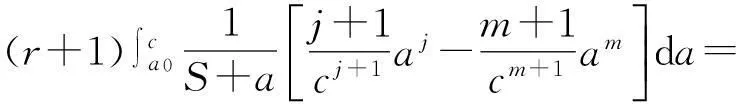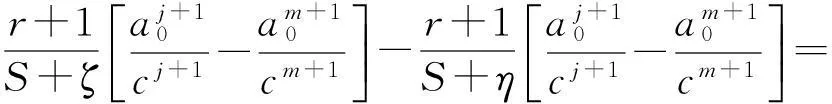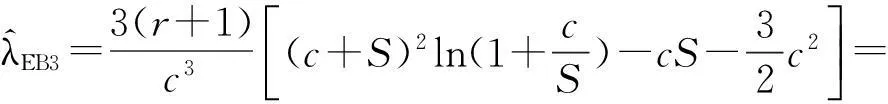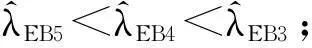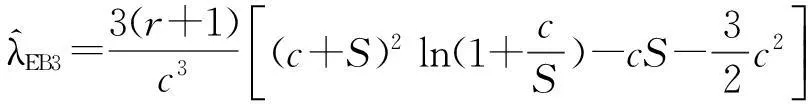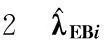指数分布参数的E-Bayes方法
2016-01-05李亿民
李亿民
(山东理工大学理学院, 山东淄博255049)
指数分布参数的E-Bayes方法
李亿民
(山东理工大学理学院, 山东淄博255049)
摘要:基于指数分布定时截尾寿命试验,给出了失效率λ的E-Bayes估计.研究了在超参数取不同密度函数时λ的E-Bayes估计之间的关系和收敛速度以及估计量关于超参数的稳健性,并通过实例,给出了不同超参数下失效率λ和可靠度R(t)的计算结果.
关键词:指数分布;先验分布;超参数;失效率;E-Bayes估计
对于指数分布的定数截尾寿命试验,已经有了比较成熟的处理方法[1].对于定时截尾寿命试验,在规定的试验时间较短时,特别是对于高可靠产品,失效个数往往比较少,甚至出现无失效的情形[2-6].为了充分利用产品的失效信息和分布的先验信息,对指数分布定时截尾寿命试验,我们试图给出参数λ和R(t)的E-Bayes(expected Bayesian)估计[5].
设产品寿命T服从参数为λ的指数分布,即
T~f(t)=λexp{-λt},t>0
(1)
其中λ>0为产品的失效率.
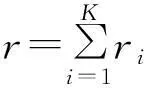
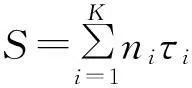
1失效率λ的Bayes估计和E-Bayes估计及性质
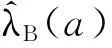
对参数λ>0,选择其先验密度函数为[5]
π(λ|a)=aexp(-aλ),λ>0
(2)
其中a>0为超参数.
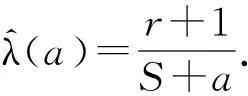
证明对指数分布,在第i组定时截尾寿命试验中,其失效数ζi服从参数为(ni-ri)τiλ的Poisson分布,于是样本的似然函数为
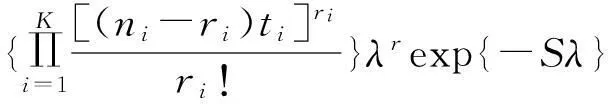
由Bayes定理,得参数λ的后验密度
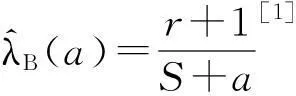
由于知道a>0,我们假定它有上界c,即a服从 (0,c)上的分布,为此,假定其密度函数分布为
(3)
(4)
其中j≥0,当j=0时,即为(0,c)上的均匀分布;两种密度函数从图形上差别较大,式(3)为严格递减函数,式(4)为严格递增函数.

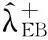
(ⅱ)对任意m>0,j>0,有

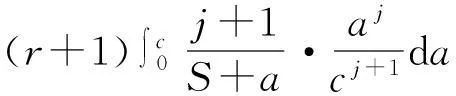
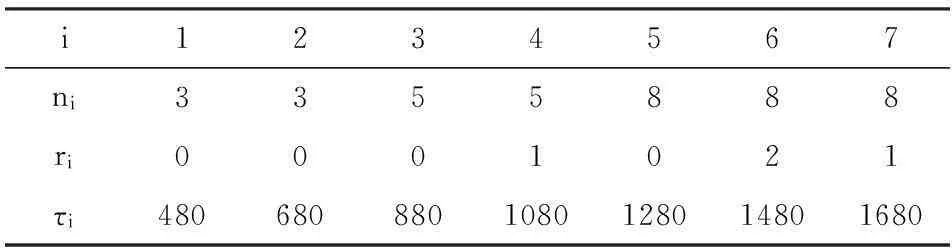
对任意0≤j (5) 为便于应用,我们给出k=2,0时a的3个先验密度函数 (6) (7) (8) 定理3在定理1的条件下,若a的3个先验密度函数为式(6)、式(7)、式(8),则 (ⅰ)参数λ的E-Bayes估计分别为 证明(ⅰ)由定义1知 至于其他两种情况,可类似证明. 至于(ⅲ)和(ⅳ)的证明,直接利用(ⅰ)的结果即可. 2 应用实例 某型号电子产品的定时截尾试验中,所得到的试验数据见表1.已知该产品寿命服从参数为λ的指数分布. 表1 电子产品寿命试验数据 s 表和的计算结果 参考文献: [1]茆诗松,汤银才,王玲玲. 可靠性统计[M]. 北京:高等教育出版社,2008. [2]茆诗松,程依明,濮晓龙. 概率论与数理统计教程[M]. 2版.北京:高等教育出版社,2011. [3]茆诗松, 李亿民. 恒加寿命试验中无失效数据的处理[J]. 应用概率统计, 1993,9(2) :216-218. [4]李建军. 指数分布无失效数据的Bayes点估计[J]. 桂林电子科技大学学报,2007,27(1):68-70. [5]韩明. 可靠性参数的修正Bayes估计法及其应用[M]. 上海:同济大学出版社,2010. [6]黄秀平,周经伦.二项分布场合加速退化零失效可靠性验证试验[J]. 系统工程与电子技术, 2012,34(9):1 951-1 956. [7]华东师范大学数学系. 数学分析[M]. 4版.北京:高等教育出版社,2010. [8]熊莲花,赵德勤. 威布尔分布无失效数据失效概率的估计[J]. 大学数学,2010,26(3): 23-27. [9]马志明,刘瑞元. 指数分布无失效数据情形的参数估计[J]. 青海大学学报:自然科学版,2007,25(2):82-85. (编辑:郝秀清) 收稿日期:2014-09-09 作者简介:李亿民,男, lym640722@163.com. 文章编号:1672-6197(2015)02-0040-04 中图分类号:O213.2 文献标志码:A An E-Bayesian method for parameters of exponential distribution LI Yi-min (School of Science, Shandong University of Technology, Zibo 255049, China) Abstract:Based on the Type-Ⅰcensoring life test under the exponential distribution condition,the E-Bayesian estimation of failure rate λ is presented in this paper. The relationship and convergence rate of the E-Bayes estimation of λ are considered when super parameters select different density functions, and the robustness of estimator related to super parameter is discussed. Some examples have been appliedto calculate failure rate λ and reliability R(t) under different super parameters. Key words:exponential distribution; prior distribution; super parameter; failure rate; E-Bayesian estimation