q元码重量分布的MacWilliams变换
2016-01-05曹永林
高 云, 曹永林
(山东理工大学理学院, 山东淄博 255049)
q元码重量分布的MacWilliams变换
高云, 曹永林
(山东理工大学理学院, 山东淄博 255049)
摘要:根据Krawtchouk多项式和 q元码 C重量计数器的性质给出 q元码 重量分布的MacWilliams变换,然后利用此变换得到 q元码重量分布的刻画,最后利用 q元码重量分布的MacWilliams变换和距离分布的性质给出 q元码距离分布的刻画.
关键词:q元码; 重量分布; MacWilliams变换
近年来,码的重量分布[1-2]和距离分布成为编码理论的一个研究热点.重量分布是码的重要参数之一,它能反应码的纠错能力并且在译码过程中能计算误差检测和校正的错误概率.此外,码的重量分布还与格理论与不变量理论有密切联系.万哲先在文献[3]中给出二元码重量分布的MacWilliams变换.Huffman[4]给出扩域 Fqt上的Fq-线性码重量分布的MacWilliams变换.本文将文献[3]中二元码重量分布的MacWilliams变换理论推广到任意q元码.文章先给出q元码C-v重量分布的MacWilliams变换,再利用此变换得到q元码C的重量分布和距离分布的刻画.文章中用到的某些概念和符号见文献[5].
1预备知识
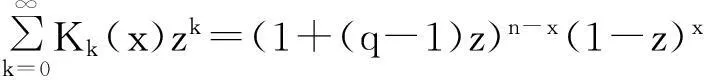
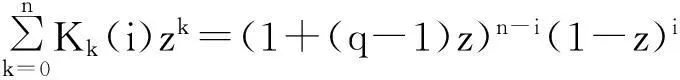
(1)
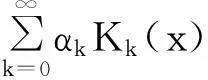
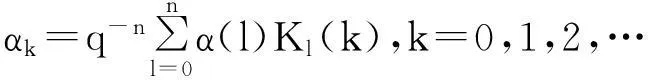
(2)
2q元码重量分布的MacWilliams变换

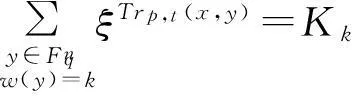
(3)

Ai(v)=|{c-v|c∈C,w(c-v)=i}|,
(4)
则{A0(v),A1(v),…,An(v)}叫做平移C-v的重量分布.令
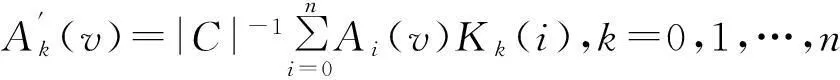
(5)

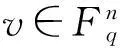
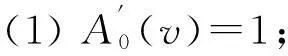
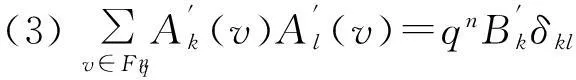


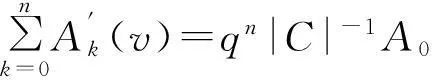
(3)由式(3),式(4)和式(5)得

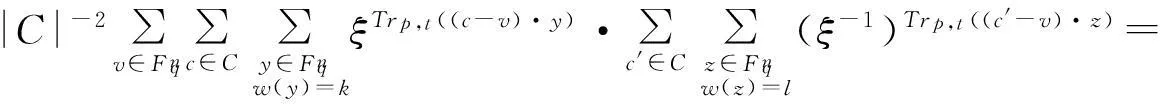
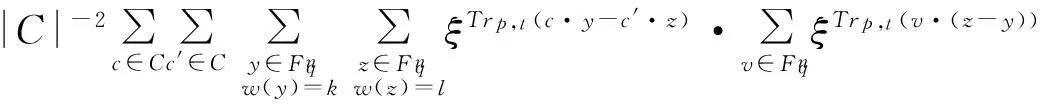
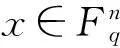
在(1)式中令z=1,则有


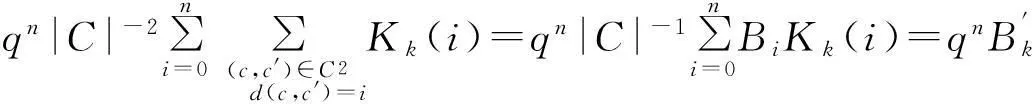

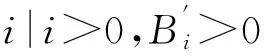
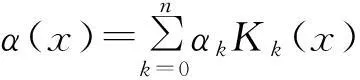

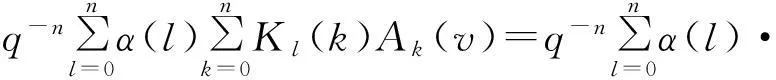

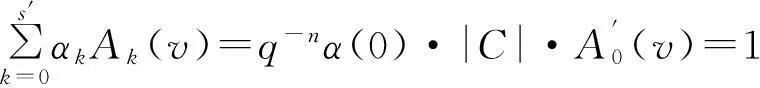
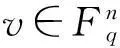
参考文献:
[1] Zheng D B, Wang X Q, Hu L,etal. The weight distributions of two classes ofp-ary cyclic codes[J]. Finite Fields Appl, 2014, 29: 202-224.
[2] Li X J, Yue Q, Li F W. Weight distributions of cyclic codes with respect to pairwise coprime order elements[J]. Finite Fields Appl, 2014, 28: 94-114.
[3] Wan Z X. Quaternary codes[M]. Singapore: World Scientific Publishing Co Pte Ltd, 1997: 20-34.
[4] Huffman W C. On the theory ofFq-linearFqt-codes[J].Adv Math Commun, 2013, 7(3): 349-378.
[5] 高云,常星星,肖凌.q元码距离分布的MacWilliams变换[J].山东理工大学学报:自然科学版,2014,28(4):72-74.
(编辑:刘宝江)
收稿日期:2014-06-16
作者简介:高云,女,gaoyun2014@126.com; 通信作者:曹永林,男,ylcao@sdut.edu.cn
文章编号:1672-6197(2015)02-0048-03
中图分类号:TN911.22
文献标志码:A
MacWilliamstransformsoftheweightdistributionsofq-arycodes
GAOYun,CAOYong-lin
(SchoolofScience,ShandongUniversityofTechnology,Zibo255049,China)
Abstract:The MacWilliams transform of the weight distribution of a q -ary code C is given by the properties of Krawtchouk polynomials and weight enumerators of q -ary codes. Then, the weight distribution of a q -ary code is obtained by the MacWilliams transform. At last, the distance distribution of a q -ary code is obtained by the MacWilliams transforms and the properties of the distance distribution of q -ary codes.
Key words:q-ary code; weight distribution; MacWilliams transform
