基于非线性规划的磁饱和电抗器优化设计
2016-01-05杜钦君张志见
石 翔, 杜钦君, 马 浩, 徐 帅, 张志见
(1. 山东理工大学 电气与电子工程学院, 山东 淄博255049;
2. 国网山东烟台市牟平区供电公司, 山东 烟台264100)
基于非线性规划的磁饱和电抗器优化设计
石翔1, 杜钦君1, 马浩1, 徐帅1, 张志见2
(1. 山东理工大学 电气与电子工程学院, 山东 淄博255049;
2. 国网山东烟台市牟平区供电公司, 山东 烟台264100)
摘要:磁饱和电抗器的设计主要依靠经验公式和经验参数,试制出样机后,根据设计指标与样机指标的偏差修改设计方案,该方法存在设计精度较低、成本较高的缺点.在磁饱和电抗器设计中,根据约束条件,借助计算机寻优对目标函数求极值,可计算出最适合的设计参数,从而缩短了设计周期,明显降低了设计及制造成本.
关键词:磁饱和电抗器; 非线性规划; 优化设计
磁饱和电抗器具有稳定、可靠、稳定运行时间较长等优点,大功率磁饱和电抗器可应用于低压及高压交流电动机限流软起动和动态无功补偿[1-6].磁饱和电抗器的设计主要依靠经验公式和经验参数,参数选择随意性大,备选方案多.试制出样机后,根据偏差做调整,设计精度较低,成本较高.将优化原则引入磁饱和电抗器设计中,借助计算机寻优,可缩短设计周期,降低成本.
文献[7]提出了基于量子粒子群算法的电力变压器优化设计方法,文中提及该方法可适用于其他电气设备优化设计的求解过程,提高求解过程的收敛速度.文献[8-9]给出了基于不同算法的空心电抗器的优化设计方法,证明了在空心电抗器设计中应用优化设计方法,可缩短设计周期.但上述文献都没有给出与磁饱和电抗器有关的设计方法.文献[10]提出了一种磁饱和电抗器的简易设计方法,可运用公式解析法求得电抗器尺寸,但文中提及应用这种设计方法,存在硅钢片数量和控制绕组铜线的用量较大的问题.文献[11]论证了在多目标优化设计中可使用线性加权法求得数值解.本文针对现存的磁饱和电抗器优化设计方面的不足,提出基于非线性规划的磁饱和电抗器设计方法,以硅钢片、绕组铜线和运行费用作为多目标函数,选择设计变量作为约束条件,应用线性加权法对优化设计进行求解,以80kVA磁饱和电抗器为例,验证优化设计的可行性.
1磁饱和电抗器多目标优化设计
1.1 优化设计的数学模型
应用优化算法,计算出一组设计参数,以较高的性价比实现设计指标.
在设计过程中,习惯将设计参数称为设计变量,为求得优化设计的数值解,将设计目标表示成设计变量x1,x2,…,xn的非线性函数,即f(x1,x2,…,xn),简写为f(x),f(x)即为目标函数.
在优化设计中必须满足的设计指标称为约束.为求得满足约束条件的数值解,常表示为等式或不等式的形式,如:

(1)
故优化设计可转换为存在约束的求解目标函数极小值.数学上称之为非线性规划,其一般形式为
(2)
式中:Rn为n维欧氏空间.
1.2多目标优化问题
实际优化问题中,往往要考虑多个设计指标的优化.磁饱和电抗器的优化设计一般需求解相互制约的多个设计指标.如以设计输出功率为约束,求解功耗最低且质量最小的目标函数.由设计经验知,电抗器质量M和功耗P是相互制约的,两者的曲线关系如图1所示.这时就要折衷处理,选取最佳点.
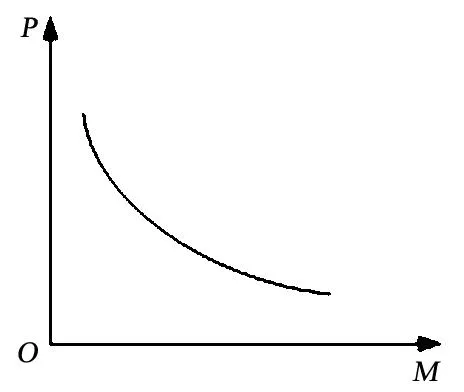
图1 磁饱和电抗器质量与功耗关系曲线
但多目标函数的求解时间较长,因此,对于多目标优化的工程设计问题,一般转化为单目标函数,完成极小值计算.常用转换方法如下:
(1)最小线性加权和.采用将多个目标函数fi(x)(i=1,2,…,m)加权求和的方法将多目标函数转换为
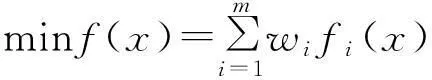
(3)
式中,wi为对fi(x)的加权因子.
(2)平方加权和的开方最小.应用此方法,可将多目标函数转换为

(4)
(3)极小极大法(Minimax Optimization).对多个目标函数求取极大者后,再求取该极大函数的极小值,可将多目标函数可转换为

(5)
2设计指标及约束条件
2.1磁饱和电抗器的设计指标
已知三相磁饱和电抗器由三个单相磁饱和电抗器组成.铁心为矩形,单相铁心结构如图2所示.
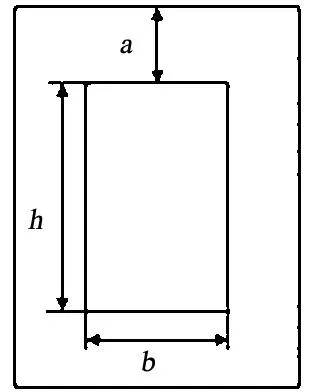
图2 可变电抗器等效电路图
本设计给定的设计指标如下:
(1)三相电源线电压为380V,频率为50Hz.
(2)磁饱和电抗器三相额定输出功率为80kVA,负载为纯电阻.
(3)工作绕组额定电流为141A.
(4)控制绕组功率为750W,最大控制绕组电流为11A.
(5)绕组温升不大于80°C.
2.2磁饱和电抗器的基本约束条件
三相磁饱和电抗器的基本约束条件为:
(1)容量约束. 为保证输出功率大于负载功率,磁饱和电抗器设计容量应大于80kVA.
设电压、电流波形为正弦,则
(6)
式中:U为电源相电压有效值;Ug及Ig分别为工作绕组上的压降和电流,R为负载等效电阻.
当铁心完全饱和时,可认为Ug=0,这时流过工作绕组的电流为
Igm=U/R
(7)
传统的磁饱和电抗器设计方法是以UIgm作为磁饱和电抗器容量,实际上,磁饱和电抗器任何工作状态通过的功率都远小于UIgm.根据设计要求,磁饱和电抗器设计容量表示为
P(x)=3UIg=3×4.44fBmScj2Sg
(8)
式中:f为电源频率,取50Hz;Bm为磁饱和电抗器的磁感应强度最大值;j2为工作绕组电流密度;Sg为工作绕组的铜线截面积;Sc为铁心截面积.

(9)
因而,可得到约束不等式为
P(x)-80000≥0
(10)
(2)铁心最大磁感应强度约束. 铁心磁密上下限约束,令在1.6~1.7T之间取值,则

(11)
(3)控制绕组电源容量约束. 通过最大控制绕组电流时,限制控制绕组电阻,以保证控制绕组功率不超过控制电源所能提供的容量;本设计的控制绕组热功率为750W.
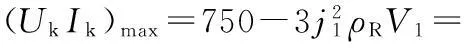

(12)
式中:ρR为铜导线电阻率(设定控制绕组工作温度100℃,取22.79);j1为控制绕组电流密度;V1为控制绕组铜线体积.
(4)温升约束. 大多数电抗器采用B级绝缘材料,一般要求最高温升不能超过80℃,因此,设计磁饱和电抗器绕组温升必须低于温升限值.
由温升计算公式
80-0.34g0.8≥0
(13)
式中:g为绕组表面热负荷.
g=(PCu/Sh)×100
(14)
(15)
Sh=3×(Sh1+0.26Sh2)
(16)
(17)
Sh2=(h-0.3)(12.5664d+1.69026)
(18)
式中:PCu为绕组温度为100°C时铜损;V2为工作绕组铜体积;Sh为有效散热面积;Sh1为控制绕组散热面积;Sh2为工作绕组散热面积.
2.3磁饱和电抗器的附加约束条件
附加约束条件是为了使电抗器具有某方面的性能而在设计时人为设定的等式约束条件.不同的附加约束条件对应着不同的设计方法.
本文采用铁心结构作为附加设计变量.即矩形铁心窗口高h;窗口宽b;铁轭宽a;铁心柱内接圆直径d;控制绕组及工作绕组电流密度j1及j2(A/mm2).
根据设计经验参数可设定如下约束:
铁心几何尺寸非负约束

(19)
铁心柱内接圆直径上下限约束

(20)
绕组电流密度下限约束

(21)
3磁饱和电抗器的优化模型
目标函数.优化目标是主要材料费及运行损耗费之和为最小.用数学形式表示为
minf(x)=C1(x)+C2(x)
(22)
式中:C1(x)为硅钢片与绕组铜线费用之和;C2(x)为铁损与铜损有关的运行费用.C1(x)可表示为
C1(x)=5500MFe+53000MCu
(23)
式中:MFe、MCu分别为三相铁心质量和三相绕组铜线质量,本设计选用宝钢B50A470,价格为5.5元/kg,铜线采用芯标称直径为1.06mm的漆包线,价格为53元/kg.

(24)
式中:ρFe为冷轧单取向硅钢片的密度,取值为7.65×103kg/m3;Kc为叠片系数,取值为0.95;Vc为一相铁心体积.
一相铁心毛体积Vc可表示为
Vc=2Sch+2adb+4ad2
(25)
硅钢片总重(三相)
MFe=3ρFeKcVc=
21.8025×(1.5931h+2adb+4ad2)
(26)
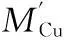
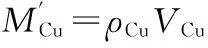
(27)
式中:ρCu=8.89×103kg/m3;VCu为绕组铜线体积.
单相绕组铜线体积为
VCu=V1+V2
(28)
三相绕组铜线质量为
MCu=3ρCuVCu
(29)
计算运行费用时,设磁饱和电抗器可连续工作15年,每年运行360d,日工作16h,工业电费取平均值为0.9元/kWh.
C2(x)=15×360×16×0.9(PCu+PFe)=
77.76(PCu+PFe)
(30)
铁损为
PFe=PcMFe=3ρFeKcVcpc=
31.613625Vc
(31)
式中:pc为比铁损,取经验参数1.45.
将式(15)、式(31)代人式(30)可得C2(x).
最终得约束条件下的目标函数的显示表达式为
(32)
4磁饱和电抗器优化设计实例
选取三个单相磁饱和电抗器组成的三相磁饱和电抗器为例,设计额定容量为80kvar、额定电压为380V.采用本文提出的优化模型,借助计算机寻优求解,对电抗器进行了优化设计.优化设计结果与原设计比较见表1.
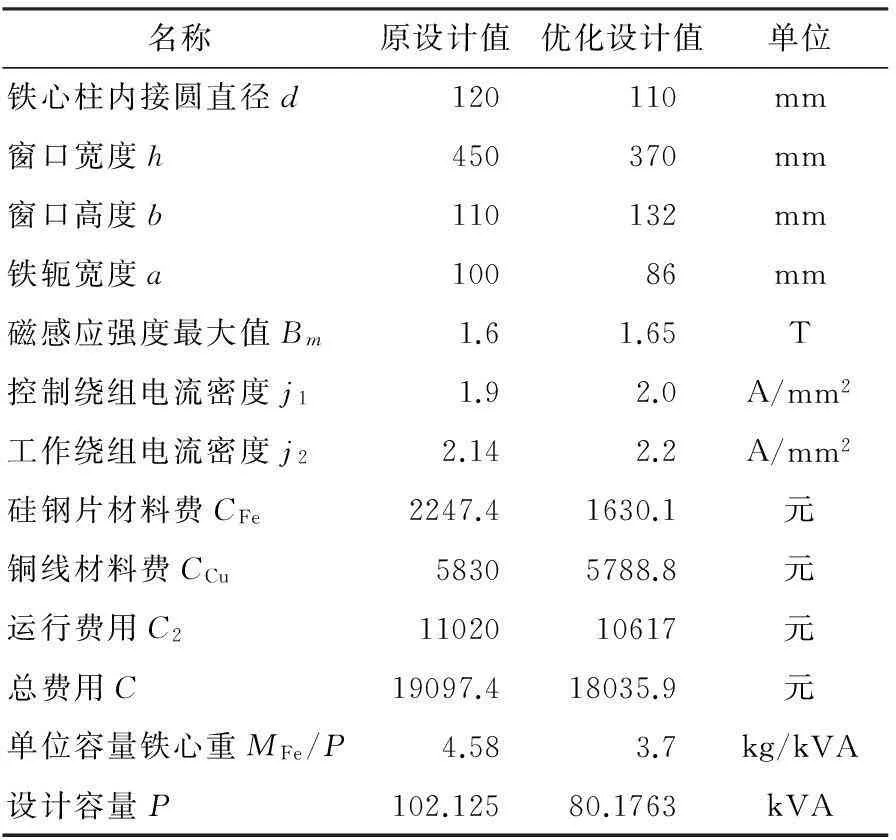
表1 优化设计结果与原设计数值比较
由表1可知:通过该方法优化可以将铁心柱内接圆直径d由120mm缩减至110mm,矩形铁心窗口高h由450mm降低至370mm;铁轭宽a由100mm缩减至86mm;与原设计比较,优化设计结果使电抗器的Bm、j1、j2略有增大,获得了较好的性能指标,同时,减少了铁心质量和铜线质量,节省了材料费用。其中,铁材料费减少617.3元,铜材料费减小41.2元,运行费用减少403元.单位容量铁重由4.58kg/kVA下降至3.7kg/kVA,材料利用更合理.
各项费用优化以后下降的百分比(以原设计值为准进行比较)见表2.

表2 优化后费用下降百分比 %
应用Ansoft Maxwell有限元分析软件建立单相电抗器3D模型,设定电抗器材料属性为电工硅钢片,选择DW315_50作为电抗器铁心材料,如图3所示.
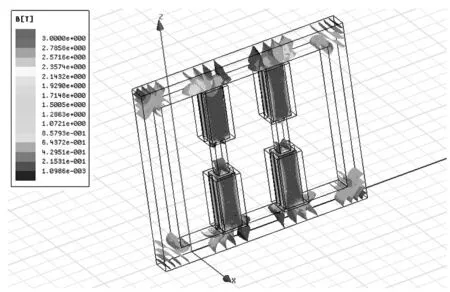
图3 磁饱和电抗器磁通密度图
由图3可知,优化后的电抗器铁心磁通密度平均在1.5T,局部最高超过3T,理论上已超过DW315_50硅钢片推荐磁感应强度值(1.8~2T),早已进入磁饱和状态,能够实现调整电抗值的功能.
5 结束语
以磁饱和电抗器的材料费用和运行费用最小作为目标函数,将非线性规划方法引入到磁饱和电抗器的设计中,建立了矩形铁心的磁饱和电抗器优化设计模型。 磁饱和电抗器优化模型是非线性规划问题,包括七个设计变量. 选取设计容量、磁感应强度、控制容量、温升约束作为基本约束条件;选取铁心几何尺寸和绕组电流密度作为附加约束条件,综合分析了四个基本约束条件的影响,给出了非线性规划的显式表达式.设计结果表明,在约束条件的限定下,优化后电抗器的各项性能指标均可满足设计要求,实现了材料费用和运行费用的多目标优化。优化设计结果中:硅钢片优化后下降幅度为27.5%,效果明显;由于导线电流密度限制,铜线体积优化后下降幅度只有0.6%,而其在目标函数占比过大,总费用下降约5.6%.采用本文构建的目标函数,对铁心质量较大的电抗器进行优化设计,优化结果费用降低明显。
参考文献:
[1]黄晓胜, 史欢, 田翠华, 等. 基于磁控电抗器的变电站无功电压控制[J]. 电力自动化设备, 2011, 31(8): 99-102.
[2]王宝安, 金丽莉, 罗亚桥, 等. 基于磁控电抗器的动态无功补偿装置[J]. 电力自动化设备, 2010, 30(4):97-100.
[3]陈博. 基于PLC的高压大电机磁控软启动装置[J]. 武汉大学学报:工学版, 2012, 45(2): 220-224.
[4]毕秀梅, 马英庆. 一种新型静止无功补偿装置[J]. 电力自动化设备, 2009, 29(8):97-100.
[5]陈锋, 赵彦珍, 马西奎. 基于QPSO算法的电力变压器优化设计[J]. 中国电机工程学报, 2009, 29(21): 99-106.
[6]潘再平, 张震, 潘晓弘. 基于QPSO算法的电力变压器优化设计[J]. 电工技术学报, 2013, 28(11): 42-47.
[7]张成芬, 赵彦珍, 邹建龙, 等. 多样性引导的改进量子粒子群优化算法及其在干式空心电抗器优化设计中的应用[J]. 中国电机工程学报, 2012, 32(18): 108-114.
[8]赵彦珍,康博,马西奎. 基于附加约束条件平衡原则的干式空心电抗器优化模型[J]. 电工技术学报, 2010, 25(11): 80-84.
[9]张成芬, 赵彦珍, 陈锋. 等. 基于改进NSGA-Ⅱ算法的干式空心电抗器多目标优化设计[J]. 中国电机工程学报, 2010, 30(18): 110-121.
[10]王玲. 一种简易饱和电抗器的设计方法[J]. 制造业自动化, 2010, 33(1):31-33.
[11]孙晓辉, 丁晓红. 结构多目标拓扑优化设计[J]. 机械设计与研究, 2012, 28(4):1-4.
(编辑:刘宝江)
收稿日期:2014-10-19
作者简介:石翔, 男, 116629689@qq.com; 通信作者: 杜钦君,男,duqinjun@sdut.edu.cn
文章编号:1672-6197(2015)02-0066-05
中图分类号:TM476
文献标志码:A
Optimizationdesignofmagneticallysaturationreactor
basedonnonlinearprogramming
SHIXiang1,DUQin-jun1,MAHao1,XUShuai1,ZHANGZhi-jian2
(1.SchoolofElectricalandElectronicEngineering,ShandongUniversityofTechnology,Zibo255049,China;
2.StateGridShandongYantaiCityMupingDistrictPowerSupplyCorporation,Yantai264100,China)
Abstract:The design of magnetically saturation reactor mainly relies on the experience formula and parameters, while parameters are chosen arbitrarily and randamly. After the prototype trial is developed, according to deviation between the predesigned index and the developed one, design adjustment is made, leading to low precision and high cost. During the magnetically saturation reactor design, the extremum of the objective function is calculated with the constraint condition by computer optimization, and the most suitable design parameters are gained, which shortens design cycle and reduces design cost. By the costs comparison, the manufacturing cost can be significantly reduced and the feasibility of design is improved by nonlinear programming.
Key words:magnetically saturation reactor; nonlinear programming; optimization design
