基于因子分析的高职综合实力研究——源自天津市高职院校的分析



基于因子分析的高职综合实力研究
——源自天津市高职院校的分析

张冠男1，王茜2

1.2.天津轻工职业技术学院，天津300350

［摘要］2011年至2014年，天津高职院校的发展已经初具规模，但发展不平衡。通过采集近4年数据平台的相关数据，本课题组研究分析了天津市26所高职院校的综合实力，并通过因子分析法，使用SPSS统计软件，将31个指标归纳于6个因子，建立了指标体系。同时研究天津高职院校在此6个因子的比重和排名，以及通过得分公式，推导出各院校综合实力的分值。

［关键词］因子分析；高职院校；教育评价体系；综合实力

［课题项目］本文系国家社会科学基金项目《“后示范时期”高职院校教育质量标准与评价体系研究》（项目编号BJA1300980）的阶段性研究成果。

2.王茜（1982—），女，汉族，天津市人，天津轻工职业技术学院讲师。研究方向：职业技术教育。

现代社会的高速发展，产业经济的不断升级整合，对高职教育提出了不同的要求。我国高职院校经过了快速发展时期，正在向成熟期过渡，发展的侧重点发生了改变，不再仅仅是量的扩充，而转向了内涵发展。这一系列变化，对高职教育质量评价体系提出了新的要求。本文参考了近15年高等教育的评估方案，以及示范校、骨干校验收标准，并通过高职院校的数据平台，对31个关键指标进行了数据分析，进而得出高职院校发展的影响因素。

一、整体构思

高职教育质量是一个综合性极强的概念范畴，其影响因素是多个方面的，既体现了当代社会发展的特点，又反映着高职教育的本质属性，进而成为评价高职教育质量的关键指标。同时，这些因素之间又有着相互影响相互促进的关系。因此，本文从数据平台选取了31个指标，作为分析的数据，涵盖了基础设施、师资结构、招生就业、资金等方面。

高职院校区别于一般本科院校的特征是注重学生职业能力的培养。因此学院不仅要具有一般的办学基础条件，而且要有体现高职特色的指标：实习实训内容、双师素质比例等。

后示范时期，校内实训基地由注重生产性实训基地建设向注重多功能服务平台建设转变。因此在指标的选取中，我们采用了职业技能鉴定等数据，体现学院的社会服务能力。

二、数据分析

（一）数据选取

本文选取了从骨干校建设之前（2011年12月数据平台），到第二批骨干校验收后（2014年12月数据平台），共计6次平台的数据。但是受限于数据的可获得性和高职间的可比性，本文选取了天津26所高职院校的31个关键指标加以分析研究。

（二）因子分析的原理

当前社会进入了大数据时代，高维变量和海量数据是面临最大的问题。因子分析法可以将多个指标通过相关矩阵的特征值计算，简化为相互独立的多个因子，同时将信息的流失把握在可控范围内。即因子分析是一种化繁为简的实用分析方法。

因子分析的数学方法是对p个原有变量x1，x2，L，xa标准化，然后采用主成分分析法，将其按照相关矩阵的特征根大小，转化为

X=AF+ε

其中，F称为公共因子；A称为因子载荷矩阵，aij是第i个原有变量在第j个因子上的负荷；ε称为特殊因子，表示原有变量不能被因子解释的部分，其均值为0，相当于多元线性回归模型中的残差。

（三）数据分析结果

1.相关矩阵和KMO检验。首先，分析了31个因素的相关矩阵，发现纸质图书（低于0.073）、电子图书（低于0.327）、社会捐赠金额（低于0.345）、奖学金金额（低于0.151）、社会捐款价值（低于0.138）与其他指标相关性较弱。分析原因，对于社会捐赠、奖学金方面，个别的偶然因素较大，不能体现一个学院的整体水平。而对于图书，不仅仅是量的问题，而且应该保证质，所以不能单纯的以图书的存量为度量。因此，将这些因素删除。

KMO和Bartlett的检验

由此表可以看出，KMO检验值为0.862>0.7，Bartlett的球形度检验的近似卡方为4737.251，概率是0.000<0.05。说明这些变量间存在较强的相关性，适合做因子分析。

2．解释的总方差。观察下表，解释的总方差，第一组数据描述了初始因子解的情况，第一个特征根的解是12.970，解释了原有因素的49.883%；第2个特征根为2.036，解释了原有27个变量总方差的7.831%。其余类似，我们共选取了6个因子，共解释了77.725%。尽管第7因子的特征根和1非常接近，但是旋转后多提取一个学生获奖载荷量大的因子，因此我们只选取6个因子分析。

第2组数据，描述了因子解的情况，6个因子共解释了原有变量总方差的77.725%，可以说因子分析效果理想。

第三组数据，经过最大方差法旋转后，各因子累计方差没有变化，不影响原有变量的共态度，但是，重新分配了各个因子解释原有变量的方差，改变了各个因子的方差贡献，使得因子更易于解释。

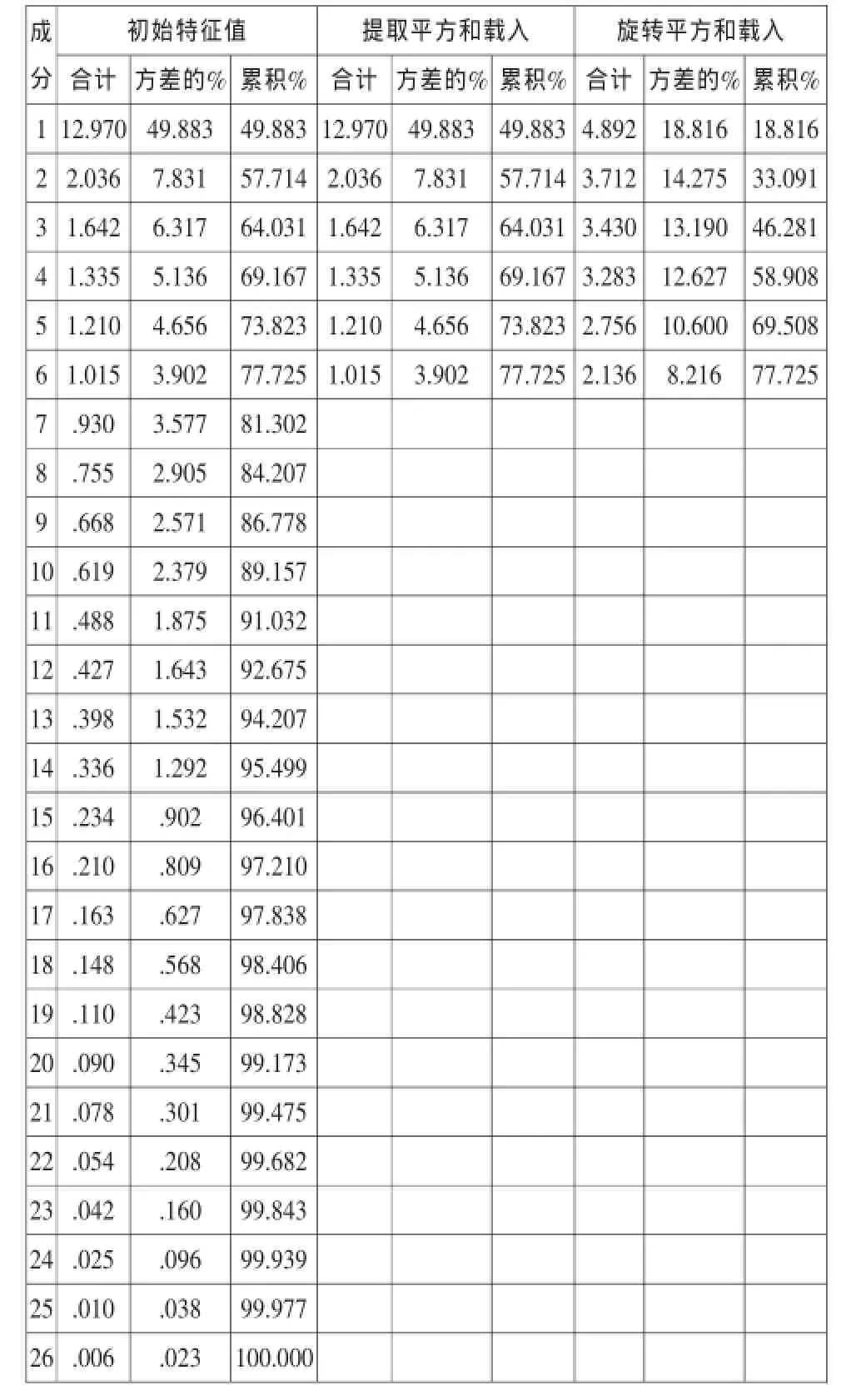
解释的总方差

3.成分矩阵。成分矩阵又称为因子载荷矩阵，根据该表，我们可以写出因子计算公式。例如：

全日制高职招生数=0.929×因子1+0.058×因子2-0.072×因子3+0.124×因子4-0.022×因子5-0.107×因子6

全日制普通高职在校生总数=0.921×因子1-0.019×因子2-0.132×因子3+0.211×因子4-0.120×因子5-0.088×因子6

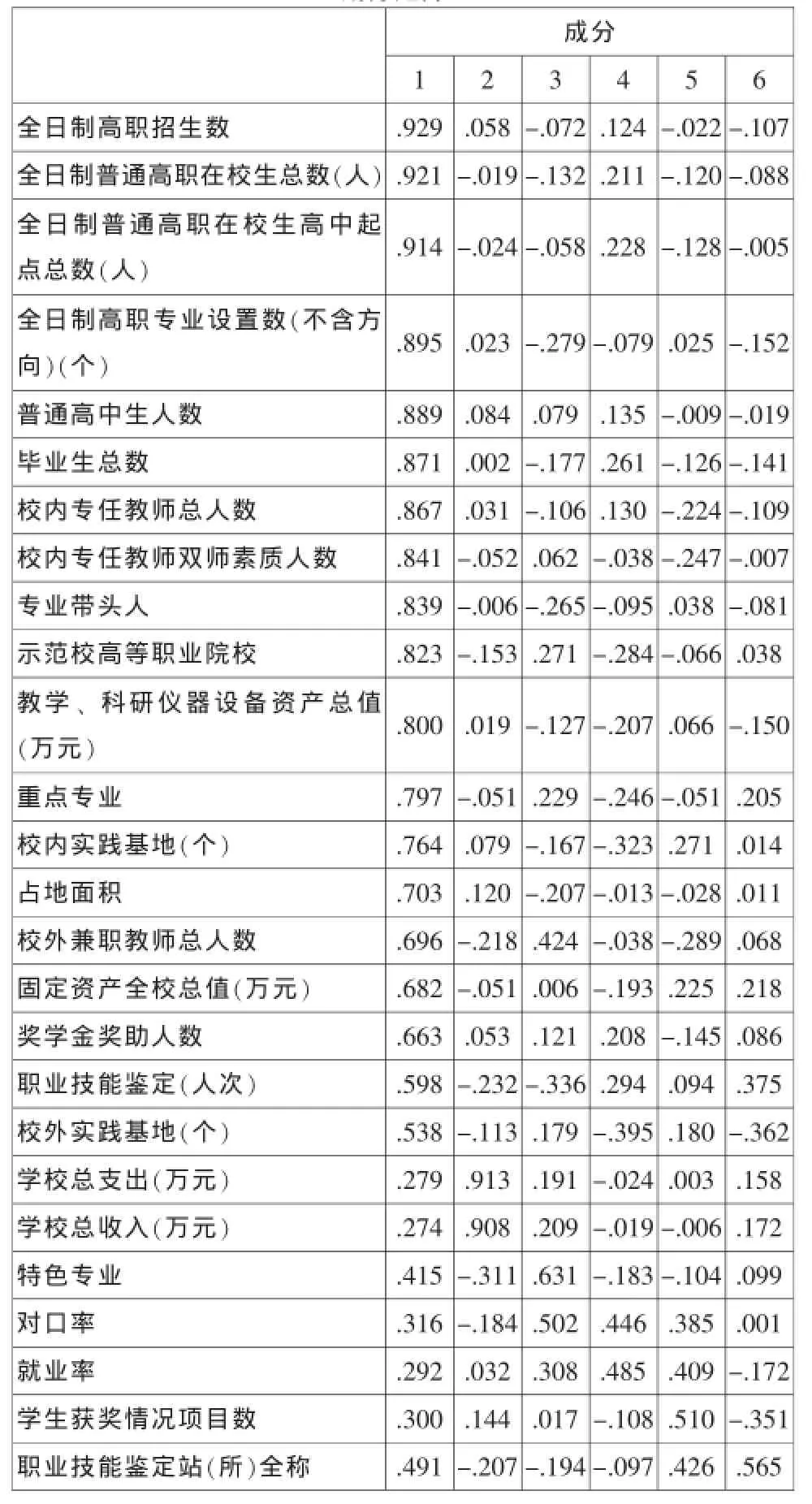
成分矩阵a

通过此表看出26个指标在第一因子上的载荷都很高，意味着他们和第1个因子的相关程度极高，第1个因子重要性突出。后面的因子对原有变量的解释作用不显著。

4.旋转成分矩阵。本文选取的是方差最大法对因子载荷矩阵实行正交旋转，以便因子具有命名解释。

观察此表，可以看出第一个因子，主要解释了这些变量。第一个因子一般院校所需具备的基本办学条件，作为高职所特有的是，高中学生比例、双师素质比例。

第二个因子解释为专业影响力，这里包含了国家或市级的重点、特色专业，同时说明了本校此类专业在行业中的地位，同时示范校高等职业院校，包含了示范校、骨干校的分类，进一步表明该学院在全国的影响力。校外兼职教师一方面体现了学院对兼职教师的制度政策，同时也反映了该校启用本行业内教师的力度。

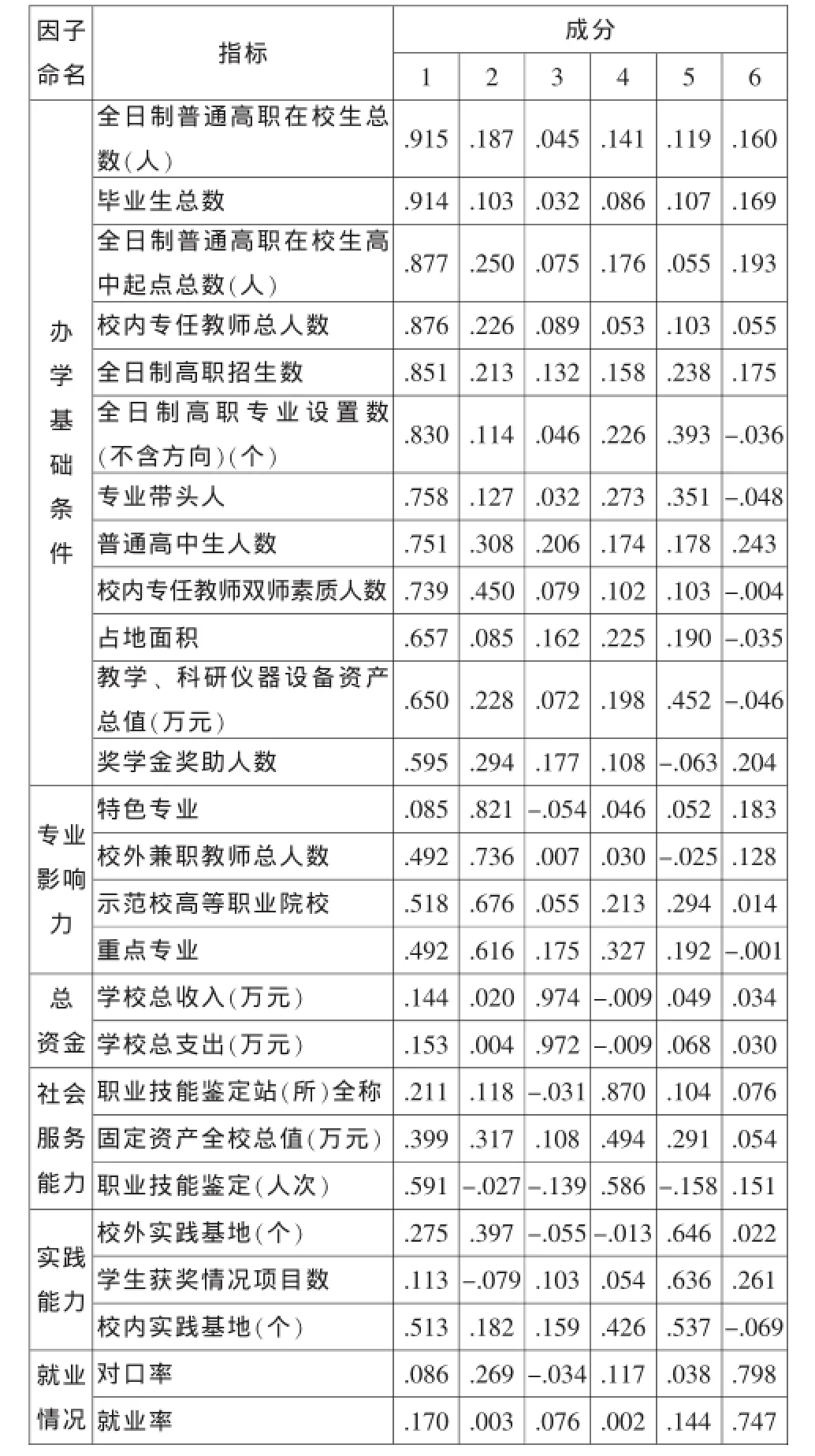
旋转成分矩阵a

第三个因子是学院的整体资金情况。

第四个因子解释为社会服务能力，主要是学院在职业技能鉴定上的突出作用。这里将固定资产全校总值纳入其中，主要考虑到资产对于设备装备的辅助作用，对于职业鉴定的促进。

第五个因子是实践能力。主要考察了学生的实践基地个数、实践能力（技能大赛获奖）、实习实训基地设施的完备。

第六个因子涉及到学生的就业情况。高职院校培养技术技能型人才，因此学生的就业率是一个重要指标，同时专业对口率考量了学生的技术能力和学院的师资水平，因此是一个较重要指标。

成分得分协方差矩阵表明这6个因子没有线性相关性，满足因子分析的要求。

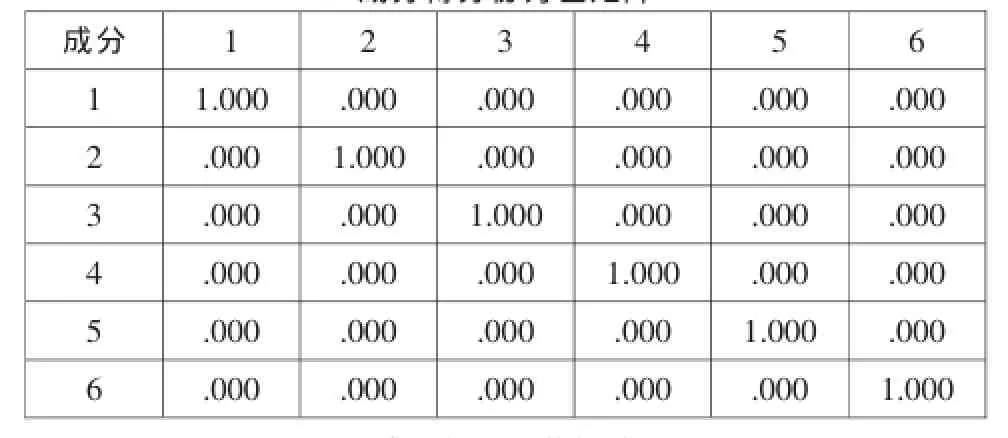
成分得分协方差矩阵

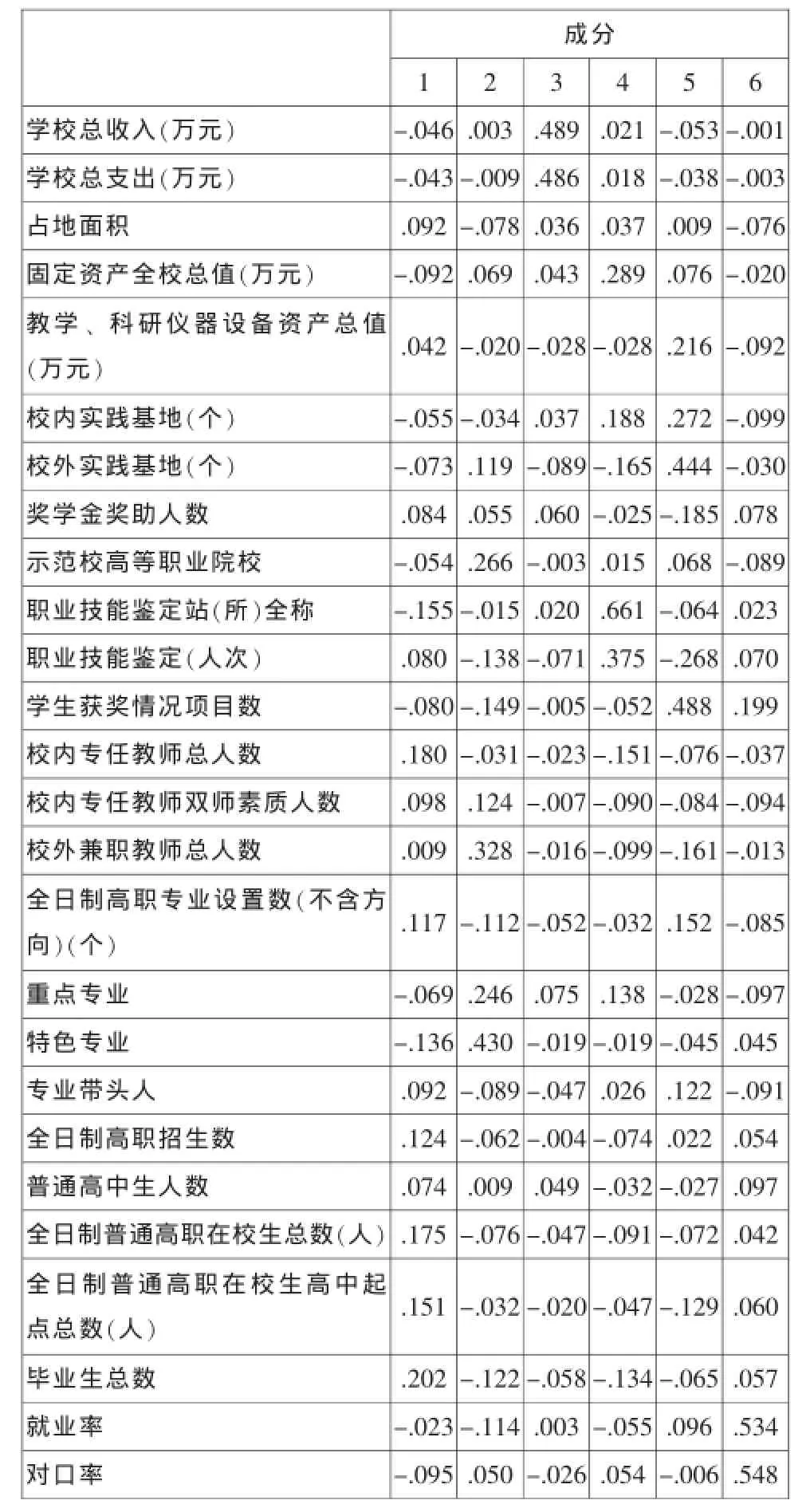
成分得分系数矩阵

5.计算因子得分。本文采用的是回归法计算因子得分系数。

通过此表可以计算出6个因子的分值。根据这27个因子的原始数值乘以本表中因子所对应的数值，可以得出26所高职院校的各因子的分值。根据旋转后的因子得分可以得到，最终各个高职院校的综合实力得分公式为：

学校综合实力分值=0.458142*f1+0.153992*f2+ 0.106711*f3+0.101494*f4+0.101245*f5+0.078415*f6

通过因子得分，可以看出各高职院校在上述方面的分值，进而可以得到排名。这样各个院校可以了解本学院在办学基础条件、专业影响力、总资金、社会服务能力、实践能力、就业情况等六个方面的情况。

当然，数据指标的不断完善，今后的研究还需进一步深入。同时对于某些专业能力的指标，只是从重点专业的个数上予以体现，还需进行专业测评，实现定性与定量相结合。

参考文献：

[1]周建松.构建开发、多元、立体的高职教育质量评价体系[J].中国高教研究，2012，（8）.

[2]刘文博.运用因子分析法构建高职学校学生学习质量评价指标体系[J].辽宁省交通高等专科学校学报，2011，（13）.

[3]李志宏.本科教学评估新方案对高职教育评估制度建设的启示[J].浙江工商职业技术学院学报，2013，（12）.

[4]陈燕清.因子分析法在高职院校理论教学质量测评中的应用[J].福建信息技术教育，2007，（2）.

[5]王成，王继顺.基于因子分析和聚类分析的学生成绩综合评价[J].甘肃联合大学学报（自然科学版），2011，（1）.

责任编辑：董跃进刘文华

A Factor-analysis Study of College Overall Strength

——Taking Vocational Colleges in Tianjin for Example

ZHANG Guan-nan1，WANG Qian2

（1.2. Tianjin Light Industry Vocational Technical College, Tianjin 300350）

［Abstract］From 2011 to 2014, vocational colleges in Tianjin have generally begun to take shape yet with development disparities. Based on the statistics collected from the data acquisition platform, the authors studied the overall strength of 26 colleges in Tianjin. Method of factor analysis and SPSS statistics program are used to reduce 31 indexes to 6 factors, thus establishing an index system. Meantime, the proportion and ranking of the 6 factors in each of the 26 colleges are also studied. In the light of the study, the overall strength score of each college is deduced according to a scoring formula.

［Key words］factor analysis; vocational college; educational evaluation system; overall strength

［作者简介］1.张冠男（1980—），女，汉族，天津市人，天津轻工职业技术学院教师。研究方向：概率论与数理统计。

［收稿日期］2015-04-22

［文章编号］2095－5537（2015）04－00008－03

［文献标识码］A

［中图分类号］G710