2015年数学高考模拟卷
2015-12-07马茂年
2015年数学高考模拟卷
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的4个选项中,只有1项是符合题目要求的.
1.设全集U={1,2,3,4},集合S={1,3},T={4},则(CUS)∪T等于( )
A.{2,4} B.{4} C.φ D.{1,3,4}
2.已知a,b是2条不同的直线,α是一个平面,则下列说法正确的是( )
A.若a∥b,b⊂α,则a∥α B.若a∥α,b⊂α,则a∥b
C.若a⊥α,b⊥α,则a∥b D.若a⊥b,b⊥α,则a∥α
A.10 B.8 C.2 D.0
5.已知直线l:x+y-9=0和圆M:2x2+2y2-8x-8y-1=0,点A在直线l上,B,C为圆M上的2个点,在△ABC中,∠BAC=45°,AB过圆心M,则点A横坐标的取值范围为( )
A.[2,6] B.[0,6] C.[1,6] D.[3,6]
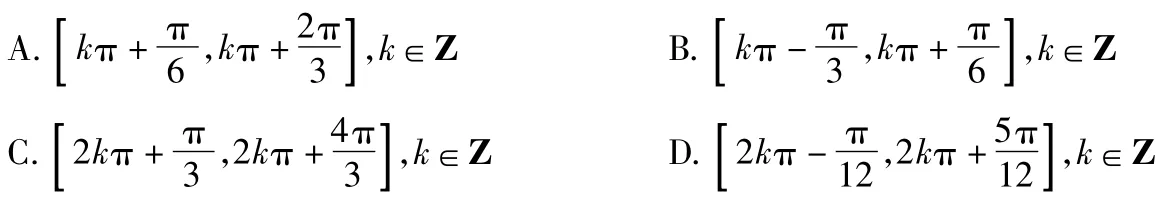
7.如图1,在正三棱柱(底面是正三角形、侧棱垂直于底面的三棱柱)中,AB=AA1=1,若点P在平面
ABC内运动,使得△AC1P的面积为,则动点P的轨迹是( )
A.圆 B.椭圆 C.双曲线 D.抛物线

图1
8.(理)已知对于正整数a,存在一个以a为二次项系数的整系数二次三项式,具有2个不相等且小于1
的正根,那么a的最小值为( )
A.1 B.2 C.3 D.5

二、填空题:本大题共7小题,第9题至第12题每小题6分,第13题至第15题每小题4分,共36分.把答案填在题中横线上.
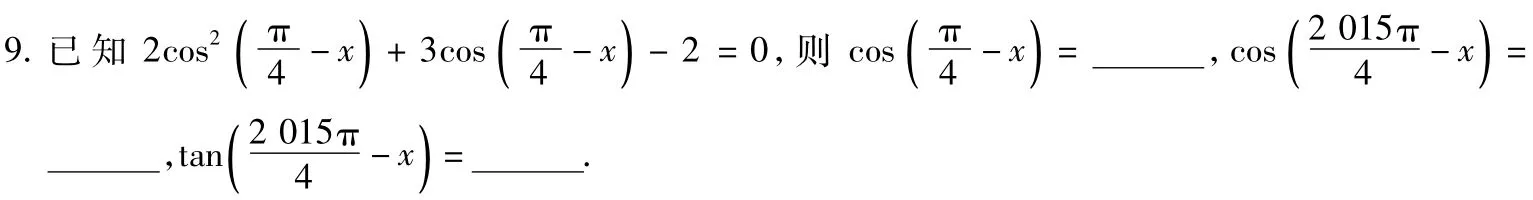
10.图2是一个几何体的三视图,则该几何体是______,其表面积为______.
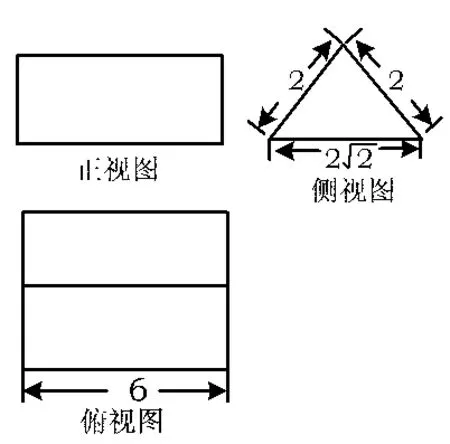
图2
11.已知-1,4是方程ax2+bx+c=0的2个根,且a>0,则4a+c=______,的最小值为______.
13.等差数列{an},{bn}的前n项和分别为Sn,Tn,若对任意的正整数n都有,则=______;
若二次函数f(x)=x2+2mx+2m+1的2个不同零点均在(0,1)内,则实数m的取值范围是______.
15.(理)过抛物线y2=4x的焦点作一倾斜角为α、长度不超过8的弦,弦所在的直线与椭圆3x2+2y2=2有公共点,则α的取值范围为______.
(文)已知椭圆C1:,双曲线C2:(其中a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近
线交于点A,B,且C1与该渐近线的2个交点将线段AB三等分,则C2的离心率为______.
三、解答题:本大题共5个小题,共74分.解答应写出文字说明、证明过程或演算步骤.
16.(15分)已知在△ABC中,角A,B,C所对的边为a,b,c,其面积S满足,且的夹角为θ.
1)求θ的取值范围;
17.(15分)(理)如图3,已知ABCD是正方形,直线AE⊥平面ABCD,且
AB=AE=1.
1)求异面直线AC,DE所成的角;
2)求二面角A-CE-D的大小;
3)设P为棱DE的中点,在△ABE的内部或边上是否存在一点H,使PH⊥平面ACE?若存在求出点H的位置,若不存在说明理由.
(文)在数列{an}中,a1=1,an+1=2an-n+2(其中n∈N*).
1)求证:数列{an-(n-1)}是等比数列;
2)记数列{an}的前n项和为Sn,求数列的前n项和Tn.

图3
18.(15分)(理)如图4,已知A是圆x2+y2=4上的一个动点,过点A作2条直线l1,l2,它们与椭圆都只有1个公共点,且分别交圆于点M,N.

图4
1)若A(-2,0),求直线l1,l2的方程.
2)①求证:对于圆上的任一点A,都有l1⊥l2成立;②求△AMN面积的取值范围.
在的平面垂直,且AN=AB=2BM,E,F,P分别是线段NC,AB,MC的中点.
1)求证:EF∥平面MBC;
2)求异面直线AB与ME所成角的余弦值;
3)求四面体PBMF的体积.

图5
19.(15分)(理)已知数列{an}中,a1=8,a4=2且满足an+2-2an+1+an=0(其中n∈N*).
1)求数列{an}的通项公式.
(文)已知抛物线x2=4y的焦点为F,A,B是抛物线上的2个动点,且(其中λ>0).过点A,B分别作抛物线的切线,设其交点为M.
2)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
20.(14分)(理)已知函数f1(x)=e|x-2a+1|,f2(2)=e|x-a|+1(其中x∈R).
1)若a=2,求f(x)=f1(x)+f2(x)在x∈[2,3]上的最小值;
2)若x∈[a,+∞)时,f2(x)≥f1(x),求a的取值范围;
(文)定义在R上的奇函数f(x),当x≥0时,f(x)=-x2+2x.另一个函数y=g(x)的定义域为[a,b],值域为,其中a≠b且a≠0,b≠0.在x∈[a,b]上,f(x)=g(x).问:是否存在实数m,使集合{(x,y)|y=g(x),x∈[a,b]}∩{(x,y)|y=x2+m}恰含有2个元素?
参考答案
1.A 2.C 3.B 4.C 5.C 6.A 7.B 8.(理)D(文)B

16.解1)由题意知,

由式(2)÷式(1),得

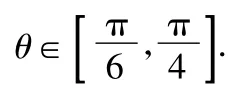
2)当S=3时,由第1)小题可得tanθ=1,即

17.(理)解法11)如图6所示,以A为坐标原点、AD为x轴、AE为y轴、AB为z轴建立坐标系,则A(0,0,0), D(1,0,0),E(0,1,0),C(1,0,1),从而,于是
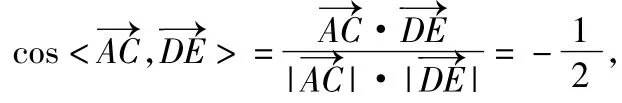
因此异面直线AC与DE所成角为60°.

令x=1,得n1=(1,0,-1),同理可得平面CDE的法向量为n2=(1,1,0),因此其法向量的夹角为60°,即二面角A-CE-D的大小为60°.

由PH⊥面ACE,得
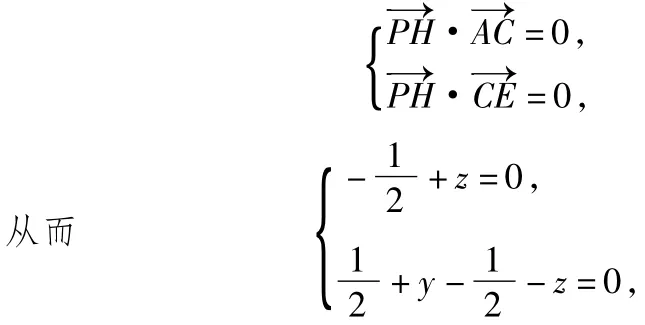
图6

图7
解法2如图7,把四棱锥E-ABCD补充成一个正方体.1)由AC∥GE,知∠DEG就是AC与DE所成的角.显然
△DEG为正三角形,故∠DEG=60°,即AC与DE所成的角为60°.
2)联结AC,BD交于点O,则DO⊥面ACE.作OM⊥CE于点M,联结DM,则∠OMD就是二面角A-CE-D的平面角,从而

于是∠OMD=60°,
故二面角A-CE-D的大小为60°.
3)存在BE的中点H,使PH⊥平面ACE.PH是△BDE中位线,PH∥BD,而BD⊥面ACE,故PH⊥平面ACE.
(文)1)证明由an+1=2an-n+2得

从而数列{an-(n-1)}是首项为1、且公比为2的等比数列.
2)解由第1)小题得

于是数列{an}的前n项和为
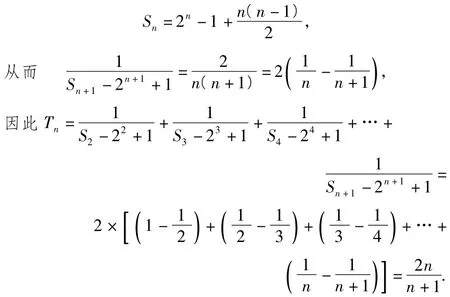
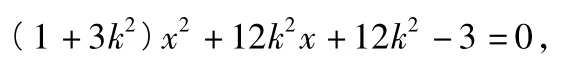
由Δ=0得,k2-1=0.设l1,l2的斜率分别为k1,k2,得k1=-1,k2=1,故直线l1,l2的方程分别为

2)①证明当l1,l2中有一条直线的斜率不存在时,不妨设l1的斜率不存在,因为l1与椭圆只有1个公共点,所以其方程为当l1的方程为时,此时l1与圆交于点,于是l2的方程为y=1(或y=-1),显然l1⊥l2.同理可证l1的方程为时,l1⊥l2.
当l1,l2的斜率都存在时,设点A(x0,y0),且,设经过点A(x0,y0)与椭圆只有1个公共点的直线为

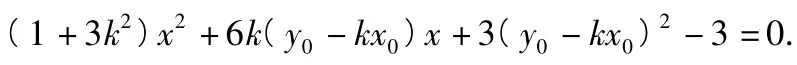
由Δ=0,化简整理得
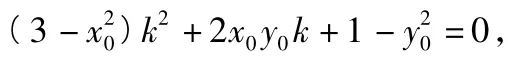
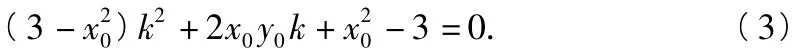
设l1,l2的斜率分别为k1,k2,因为l1,l2与椭圆只有1个公共点,所以k1,k2满足上述方程(3),从而k1k2=-1,即l1⊥l2.
综上所述,l1⊥l2成立.
②解记原点到直线l1,l2的距离分别为d1,d2,则△AMN的面积为
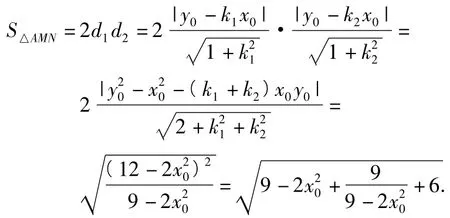

图8
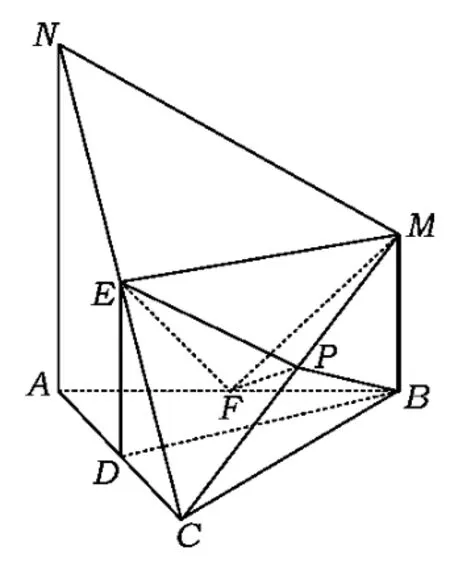
图9
(文)1)证明如图8,取线段MN的中点Q,联结QE,QF.因为QE∥MC,QF∥MB,所以平面QEF∥平面MBC.又因为EF⊂平面QEF,所以EF∥平面MBC.

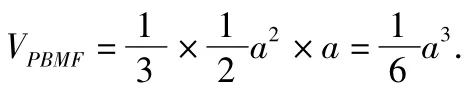
19.(理)解1)由题意可得
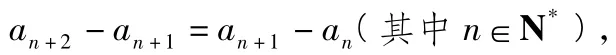
从而数列{an+1-an}是常数列.又a1=8,a4=2,故

解得a2=6,a3=4,于是a2-a1=-2,a3-a2=-2,a4-a3=-2,…,an-an-1=-2,进而

2)由第1)小题可得

则Tn=b1+b2+…+bn=
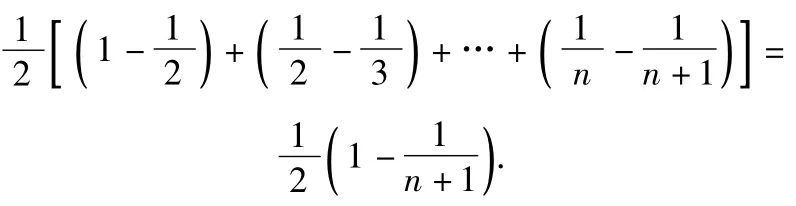
由Tn为关于n的增函数,故

(文)1)证明由已知条件,得F(0,1),λ>0,设(x1, y1),B(x2,y2).由,即得


联立式(5)和式(6)得y1=λ,,且



2)解由第1)小题知在△ABM中,FM⊥AB,从而

因为|AF|,|BF|分别为点A,B到抛物线准线y=-1的距离,所以

20.(理)解1)因为a=2,且x∈[2,3],所以

当且仅当x=2时等号成立,故f(x)在[2,3]上的最小值为2e.
2)由题意知,当x∈[a,+∞)时,
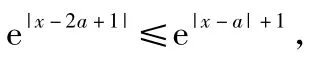
即|x-2a+1|≤|x-a|+1恒成立,从而
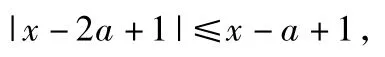
即2ax≥3a2-2a对x∈[a,+∞)恒成立.由
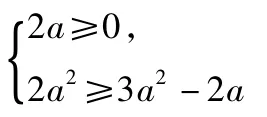
得所求a的取值范围是0≤a≤2.
3)记h1(x)=|x-(2a-1)|,h2(x)=|x-a|+1,则h1(x),h2(x)的图像分别是以(2a-1,0)和(a,1)为顶点、开口向上的V型线,且射线的斜率均为±1.
②当a<1时,可知2a-1<a,从而
1°当h1(1)≤h2(1),得|a-1|≤1,即0≤a<1时,g(x)在x∈[1,6]上的最小值为f1(1)=e2-2a;
2°当h1(1)>h2(1),得|a-1|>1,即a<0时,g(x)在x∈[1,6]上的最小值为f2(1)=e2-a.
1°当h1(6)≤1,得|2a-7|≤1,即时,g(x)在x∈[1,6]上的最小值为f1(6)=e2a-7;
2°当h1(6)>1且a≤6时,即4<a≤6,g(x)在x∈[1,6]上的最小值为f2(a)=e1=e;
3°当a>6时,因为h1(6)=2a-7>a-5=h2(6),所以g(x)在x∈[1,6]上的最小值为f2(6)=ea-5.
综上所述,函数g(x)在x∈[1,6]上的最小值为

(文)解由题意得奇函数y=f(x)在x<0时的解析式为f(x)=x2+2x,从而
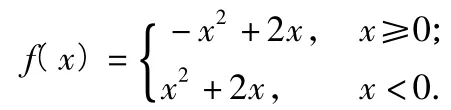
可见a,b同号,也就是说y=g(x),x∈[a,b]的图像在第一或第三象限内.根据f(x)=g(x),x∈[a,b]以及f(x)的图像可知,函数的图像(如图10所示)是曲线的一部分.由于值域与函数的单调性有关,又与定义域有关.若只考虑0<a<b<2或-2<a<b<0这2种情况,则不能准确地用a,b表示出值域区间的端点,因此要把区间(0,2),(-2,0)再分细一些,由图10中看出,当a,b>0时,可考虑以下3种情况:0<a<b≤1,0<a<1<b,1≤a<b<2.
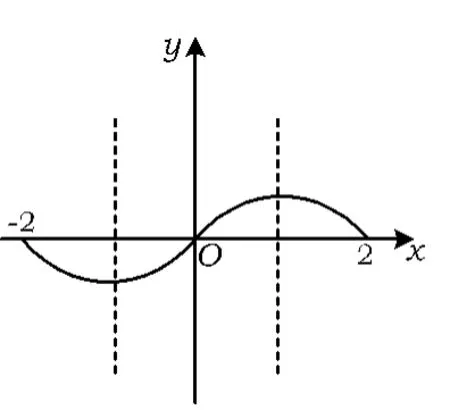
图10
②若1≤a<b<2,由图10可知g(x)是减函数,从而
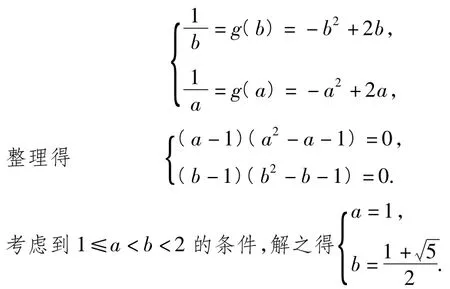
完全类似地,考虑到-1≤a<b<0,-2<a<-1<b<0,-2<b<a≤-1这3种情况后,可在-2<b<a≤-1的情况下通过值域条件得出这就得到函数

对于某个m,当抛物线与函数g(x)的图像有2个交点时,一个交点在第一象限、一个交点在第三象限.因此,m应当使方程x2+m=-x2+2x在内恰有1个实数根,并且使方程x2+m=x2+2x在内恰有1个实数根.问题归结为求m,使2x2-2x+m=0在内恰有1个实根,使在内恰有1个实数根.
方程2x-2x2=m在内恰有1个实数根,设h(x)=2x-2x2,则

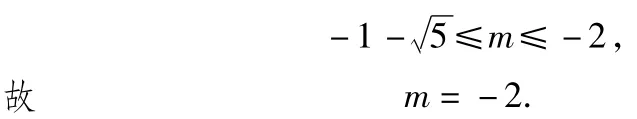
易证,抛物线y=x2-2与函数g(x)图像恰有2个交点(-1,-1)和
综上所述,m=-2.
供稿人:马茂年(杭州第十四中学)
