函数与方程思想

●周海军(镇海中学浙江宁波315200)

函数与方程思想

●周海军(镇海中学浙江宁波315200)

1 知识内容

函数的思想是用运动和变化的观点分析和研究数学中的数量关系，建立函数关系或构造函数，运用函数的图像和性质去分析问题、转化问题，从而使问题获得解决.方程的思想就是分析数学问题中变量间的等量关系，建立方程或方程组，或者构造方程，通过解方程或方程组，或者运用方程的性质去分析、转化问题，使问题获得解决.

函数与方程是2个不同的概念，但它们之间有着密切的联系.方程f(x)=0的解就是函数y=f(x)的图像与x轴交点的横坐标，函数y=f(x)也可以看作二元方程f(x)－y=0通过方程进行研究.许多有关方程的问题可以用函数的方法解决，反之，许多函数问题也可以用方程的方法来解决.

2 命题分析

函数与方程思想是中学数学核心数学思想之一，在高中数学中的地位十分重要，也是高考考查的重点之一.在历年高考中，函数与方程相关的试题一直占有相当大的份量.在高考试题中既有灵活多变的客观性试题，又有一定能力要求的主观性试题，涉及到的知识块包括高中所有知识，如三角、数列、不等式、立体几何、解析几何等.

在近几年的高考中，函数与方程思想的考查主要表现在2个方面:一是借助有关初等函数的性质，解有关求值、解(证)不等式、解方程以及讨论参数的取值范围等问题;二是在问题的研究中，通过建立函数关系式，构造中间函数，把所研究的问题转化为讨论函数的有关性质，转化为对方程的研究.

2 典题剖析

例1已知对于x的所有实数值，二次函数f(x)=x2－4ax+2a+12(其中a∈R)的值都非负，求关于x的方程的根的范围.

分析由二次函数的值都非负，知Δ≤0，可得实数a的取值范围为.而关于x的方程的根可以转化为函数g(a)=(a+2)(|a－1|+2)在上的值域问题，其解决问题的基本方法是去绝对值进行分类讨论:当时，

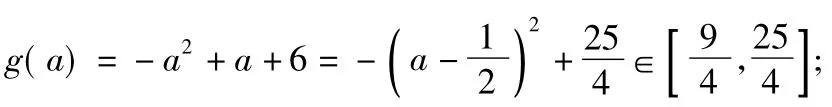
当1≤a≤2时，原方程化为

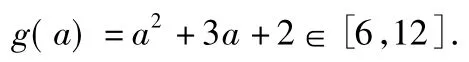
因此，所求x的取值范围即为

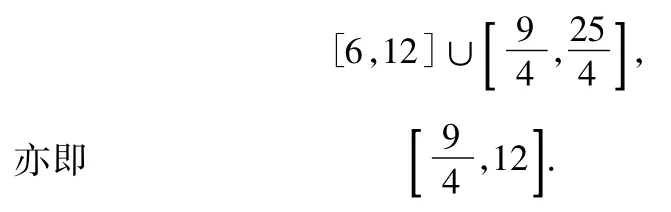
点评在此问题的解决中直接用二次函数的最值问题，同时也用到了方程与函数之间的转化.特别是方程有解问题往往通过分离系数转化为函数的值域问题.

例2已知f(x)=ax2+bx+1(其中a＞0)，设方程f(x)=x的2个实数根为x1和x2，如果|x1|＜2，|x2－x1|=2，求实数b的取值范围.

分析1设g(x)=f(x)－x=ax2+(b－1)x+1，由题意知

另一种解题思路是将a，b直接转化为x1，x2的函数关系式:

点评在解法1中运用条件得出变量a，b的关系，在求b的范围中运用方程消元的思想，消去变量a即可得到b的取值范围.在解法2中寻找变量a，b与x1，x2的关系，得到b与初始变量x1，x2的表达式，利用函数求值域的方法求b的取值范围.

例3设a∈R，若x＞0时均有［(a－1)x－1］·(x2－ax－1)≥0，则a=______.

分析从填空题的结构上看，可以从特殊值代入再验证的方法，如当x=2时，

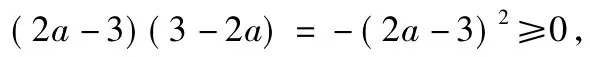
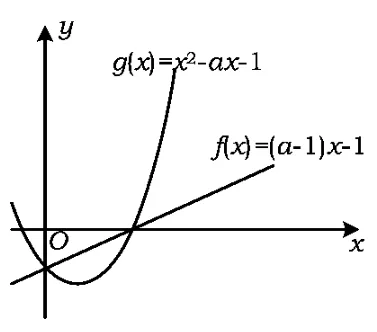
图1

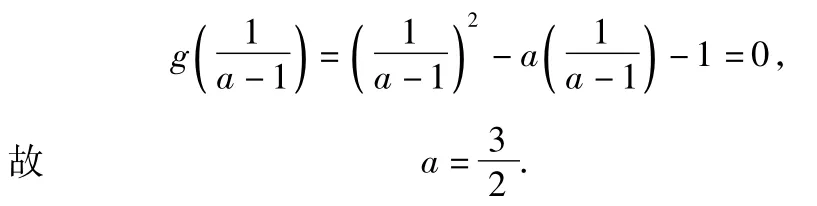
另外，也可以将主变量变为a，从而有以下的解法:

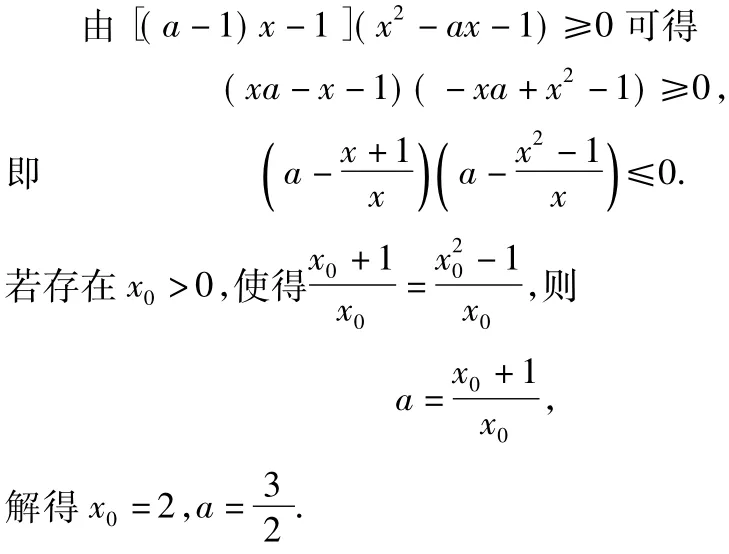
点评事实上，上述不等式等价于

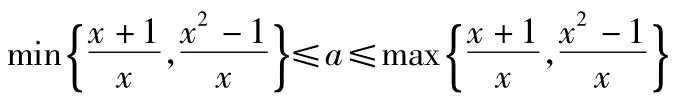
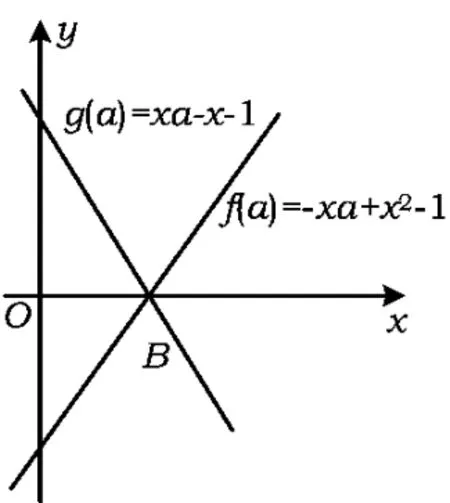
图2

它们的图像都是直线，刚好相交于x轴上的点B，则

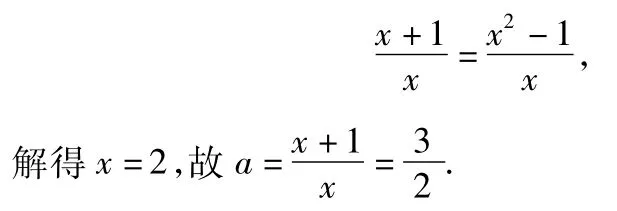
例4已知数列{an}和{bn}满足(其中n∈N*)，若{an}为等比数列，且a1=2，b3=6+b2.

1)求an，bn.

分析此题为2014年浙江省数学高考题.第1)小题利用条件得到.由{an}为等比数列，得an=2n，但要注意对q＜0的否定，进而可得bn=n(n+1).

第2)小题本质上求Sn的最大项.首先利用分组求和得到

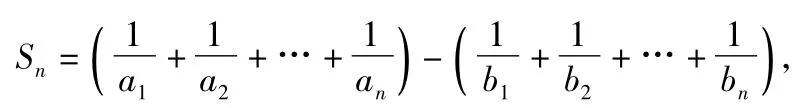
数列{Sn}的最大项则从数列{cn}的正项中分析，注意到c1=0，c2＞0，c3＞0，c4＞0，可得当n≥5时，

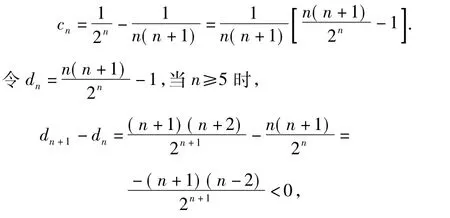
又dn≤d5≤0，即当n≥5时，cn＜0.因此，对任意n∈N*，恒有S4≥Sn，故k=4.

点评当n≥5时，cn＜0的证明上述的证法较为巧妙，如果转化为证2n＞n(n+1)，只要分析dn=2n－n(n+1)的增长规律即可，或用导数、数学归纳法、二项式定理等解决，要注意数列单调性的常用转化方法.

例5如图3，与圆(x+1)2+ y2=1相切的直线l:y=kx+t交椭圆于点M，N.若椭圆上一点C满足，求实数λ的取值范围.

图3

分析根据直线l与圆(x+ 1)2+y2=1相切，得到k，t的关系式

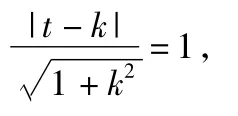
从而2kt=t2－1，且有t≠0.

基本思想是找到k，t，λ之间的关系式，利用方程思想消元，得到λ与k或λ与t的函数关系式.把y=kx+t代入并整理得

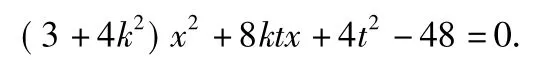
设M(x1，y1)，N(x2，y2)，则

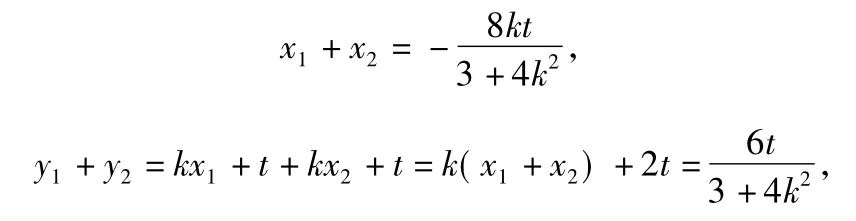
从而Δ=－48(t2－16k2－12)=

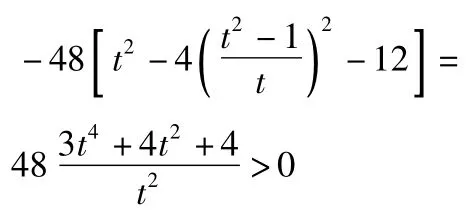
恒成立.

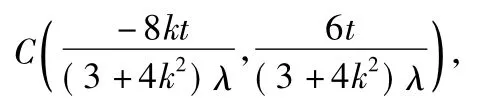
又因为点C在椭圆上，所以

因此λ的取值范围为(－1，0)∪(0，1).

点评参数的范围问题往往构建几个参数之间的方程或不等式，而问题的解决往往需要用到方程中的消元思想与函数中求值域的方法，在解决过程中要注意定义域的要求.在此题中还要注意Δ的使用，在此问题中由于圆在椭圆内，从而当直线与圆相切时，直线与椭圆必相交.

3 精题集萃

A.x1+x2＞0，y1+y2＞0

B.x1+x2＞0，y1+y2＜0

C.x1+x2＜0，y1+y2＞0

D.x1+x2＜0，y1+y2＜0

2.设Sn是公差为d(其中d≠0)的无穷等差数列{an}的前n项和，则下列命题错误的是( )

A.若d＜0，则数列{Sn}有最大项

B.若数列{Sn}有最大项，则d＜0

C.若数列{Sn}是递增数列，则对任意n∈N+均有Sn＞0

工艺过程：主反应锅中加入A相搅拌，加热至70～75 ℃，加入混合好的B相，搅拌溶解均匀后加入C相，搅拌溶解。冷却至40～45 ℃时加入D相，混合均匀，继续冷却至30～35 ℃，加入E相。搅拌均匀，至25～30 ℃时加入F相、G相，混合均匀。

D.若对任意n∈N+均有Sn＞0，则数列{Sn}是递增数列

3.设a，b，c为实数，f(x)=(x+a)(x2+bx+c)，g(x)=(ax+1)(cx2+bx+1).记集合S={x|f(x}=0，x∈R}，T={x|g(x)=0，x∈R}.若|S|，|T|分别为集合S，T的元素个数，则下列结论不可能的是( )

A.|S|=1且|T|=0 B.|S|=1且|T|=1

C.|S|=2且|T|=2 D.|S|=2且|T|=3

4.已知函数f(x)=|lgx|.若0＜a＜b，且f(a)=f(b)，

则a+2b 的取值范围是______.

6.对于满足0≤p≤4的实数p，使x2+px＞4x+p－3恒成立的x 的取值范围是______.

7.已知实数a，b，c成等比数列，且a+b+c=m(其中m＞0)，则b 的取值范围______.

8.已知集合M是同时满足下列2个性质的函数f(x)的全体:①f(x)在其定义域上是单调增函数或单调减函数;②在f(x)的定义域内存在区间［a，b］，使得f(x)在［a，b］上值域是.

1)判断函数y=－x3是否属于集合M.若不是，请说明理由;若是，请找出区间［a，b］.

9.已知数列{an}满足a1=1，(其中n∈N*)，且{a2n－1}是递增数列，{a2n}是递减数列，求数列{an}的通项公式.

参考答案

8.解1)g(x)=－x3在R上为减函数，在定义域上是单调减函数.

若g(x)∈M，则当x∈［a，b］时，

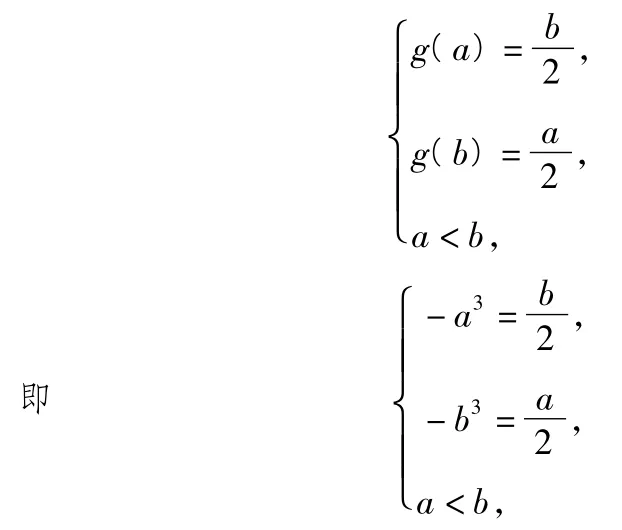
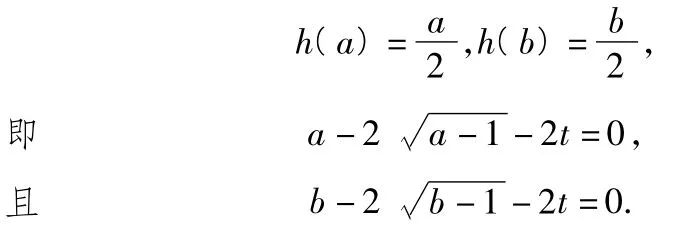
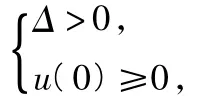
9.解由{a2n－1}是递增数列，{a2n}是递减数列，且，知

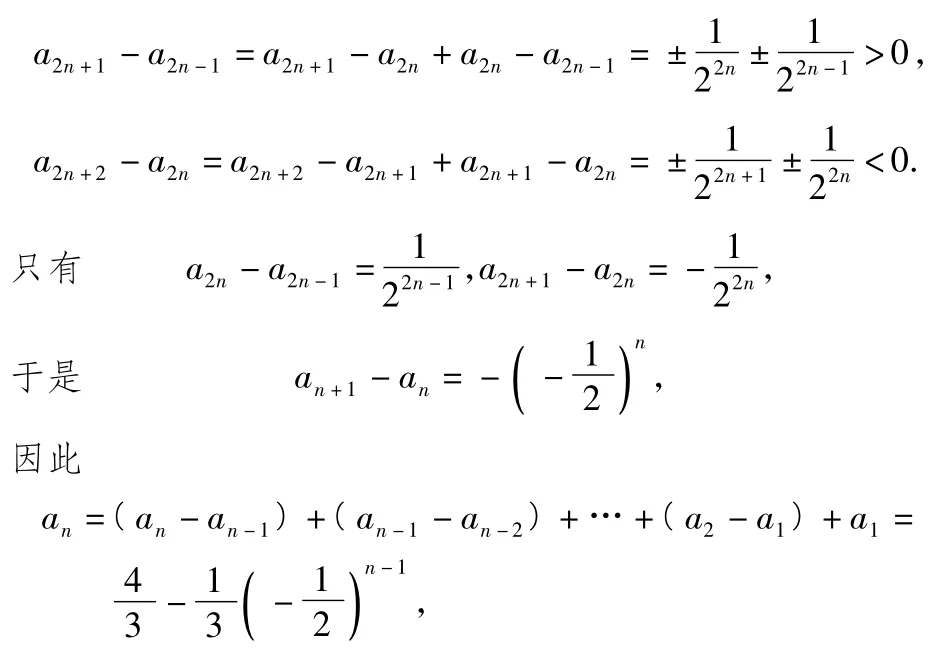
经检验，当n=1时结论也成立.故数列{an}的通项公式为

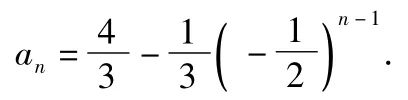
10.解依题意，直线OP的方程为y=kx.设点P(x0，kx0)，由点P在椭圆上，知

因为a＞b＞0，kx0≠0，所以

由|AP|=|OA|，A(－a，0)，得