立体几何的复习策略

●张晓东(桐乡高级中学浙江桐乡314500)

立体几何的复习策略

●张晓东(桐乡高级中学浙江桐乡314500)

1 知识内容

立体几何的主要内容有:能识别三视图所表示的几何体，理解三视图与直观图的联系并能相互转化，会计算柱、锥、台、球的表面积与体积;理解空间2条直线、直线与平面、平面与平面的位置关系，并能利用相关公理、定理证明平行与垂直这2种特殊位置关系;理解2条异面直线所成角、直线与平面所成角、二面角的概念并能利用综合法求解;掌握空间向量及其运算，并能利用空间向量解决空间的平行与垂直的证明问题，解决异面直线所成角、直线与平面所成角、二面角以及点到平面距离的计算问题.

2 命题分析

立体几何是高中数学的主干知识，在考查学生空间想象能力、逻辑推理能力以及应用与创新意识等方面有着独特的、不可替代的作用.综观浙江近几年的数学试卷，立体几何基本保持着2个小题、1个大题的格局:小题主要考查三视图、综合法求角，有时还有空间线面位置的判定，其中对三视图的考查难度有所增加，而综合法求角往往以考查空间想象能力与应用、创新意识为主，有一定难度且已经多年小题压轴，应引起重视;大题第1)小题考查空间平行与垂直的证明，第2)小题考查空间角的计算，其中平行与垂直的证明一般用综合法较容易，而对于空间角的计算，综合法与向量法各有千秋，在复习时应2种方法并重.

3 典题剖析

考点1三视图例1如图1，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( )

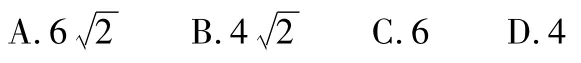
(2014年全国新课标卷I理科试题第12题)

分析本题的难点是作几何体的直观图.不妨把它置于一个正方体中(如图2)，在正方体中取3个顶点A，B，C和一条棱的中点D，通过计算不难得最长边为AD，长度为6.故选C.

图1

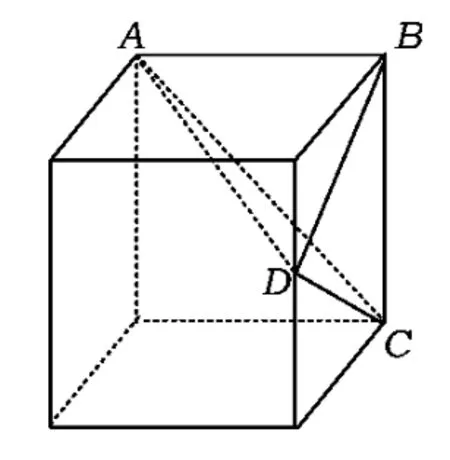
图2

考点2空间线面位置关系的判定

例2如图3，有一菱形纸片ABCD，E是AD边的一点(不包括A，D)，先将ABCD沿对角线BD折成直二面角，再将△ABE沿BE翻折到A'BE，则下列情况不可能正确的是( )

A.BC与A'BE平面内某直线平行

B.BC与A'BE平面内某直线垂直

C.CD∥平面A'BE

D.CD⊥平面A'BE

图3

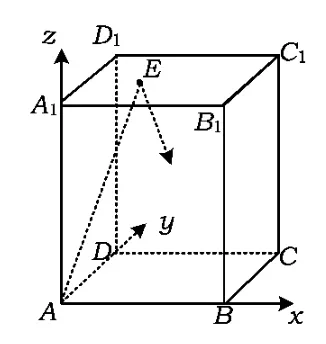
图4

分析本题主要考查空间想象能力和逻辑推理能力.显然当平面A'BE转至过BC时，选项A，B成立;联结AC，并在线段AC上取点F，使CD∥EF，A'BE翻转至A'E⊂平面BEF，CD∥平面A'BE，故选项C成立;假设CD⊥平面A'BE，可得CD⊥平面ABD，得CD⊥BD，这与∠BDC是锐角矛盾，故选项D不成立.故选D.

(2014年全国新课标卷I理科试题第12题)

考点3空间向量及空间直角坐标系

例3如图4，在长方体ABCD-A1B1C1D1中，AB=11，AD=7，AA1=12，一质点从顶点A射向点E(4，3，12)，遇长方体的面反射(反射服从光的反射原理)，将i－1次到第i次反射点之间的线段记为Li(其中i=1，2，3，4)，L1=AE，将线段L1，L2，L3，L4竖直放置在同一水平线上，则大致的图形是( )

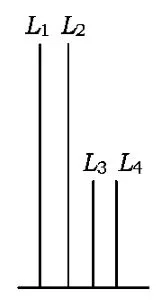
A.

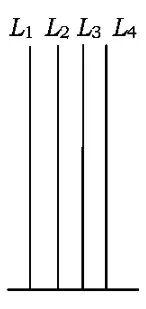
B.

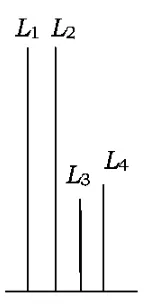
C.

D.

(2014年江西省数学高考理科试题第10题)

分析本题的关键在于将空间问题平面化.不妨将光线的运动方向分解为水平与竖直方向，如图5，在A1B1C1D1平面内，光线A1E首先与棱交于点，经D1C1反射后交C1B1于点，依次类推，并相应地作出点N，Q在底面ABCD上的射影M，P.于是光线AE，EF，FG在平

面AMNA1上，GH在平面MNQP上，如图6，易得

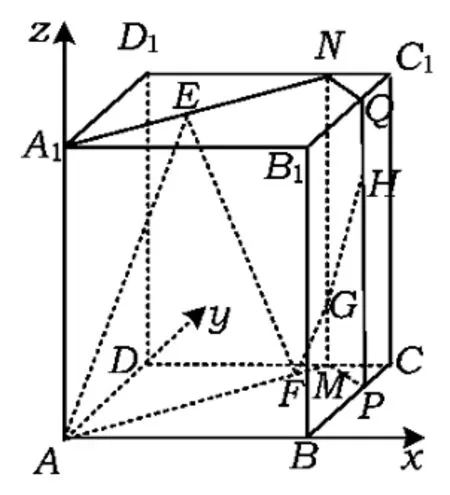
图5

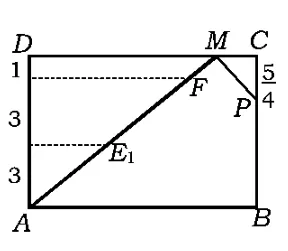
图6

故选C.

考点4射影与截面问题

例4在长方体ABCD-A1B1C1D1中，AB=4，AD=2，AA1=2，任意地翻转该长方体，则它在水平面上的投影面积最大值为( )

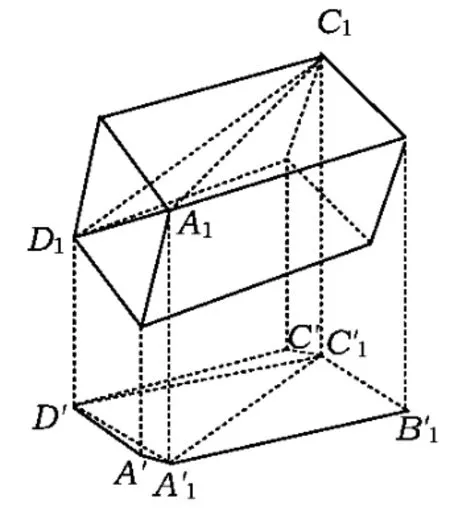
图7

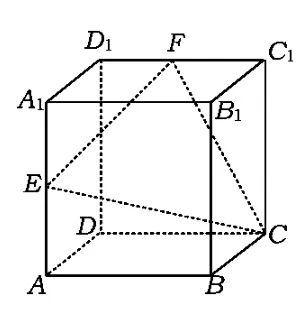
图8

分析本题的难点是弄清射影图形的形状.长方体在水平面上的投影A'A1'B1'C1'C'D'是六边形(四边形可看成六边形的退化).如图7，因为长方体每个面在水平面上的投影都是平行四边形，所以△A1'C1'D'的面积是六边形A'A1'B1'C1'C'D面积的一半.设△A1'C1'D'是长方体内△A1C1D的投影，平面A1'C1'D'与平面A1C1D所成角为θ，则S△A'1C1'D'=S△A1C1D·cosθ，显然当平面A1C1D与水平面平行时，△A1'C1'D'的面积最大.因为S△A1C1D=6，所以投影面积最大为12.故选C.

例5如图8，正方体ABCD-A1B1C1D1棱长为2，E，F分别是AA1，C1D1的中点，平面α过点A1且与平面CEF平行，则平面α截正方体所得截面的周长为______.

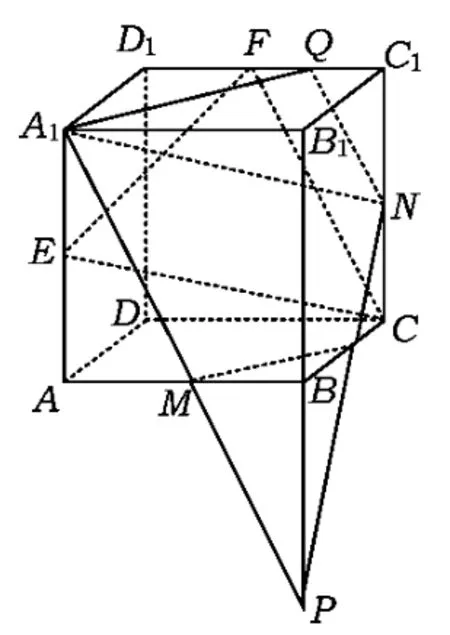
图9

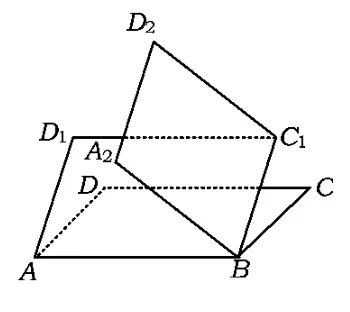
图10

分析本题的难点是作出截面.根据对称性，所求截面其实与过点C，E，F的截面全等，因此只需将过点C，E，F的截面作出计算即可.也可以取AB的中点M，CC1的中点N，显然过点A1，M，N的平面与平面CEF平行.如图9，将该截面作出，计算得

考点5翻折与展开问题

例6如图10，把一个水平放置的正方形ABCD绕AB向上转动45°到ABC1D1，再将所得正方形ABC1D1绕BC1向上转动45°到A2BC1D2，则平面A2BC1D2与ABCD所成角的余弦值为______.

分析本题主要考查应用与创新意识，难点是要找到着力点.方法1是利用平面的法向量，设3个平面的法向量分别为n1，n2，n3，并设n1，n2;n2，n3;n3，n1所成的角分别为θ1，θ2，θ，显然θ1=45°(或135°)，θ2=45°(或135°)，易得

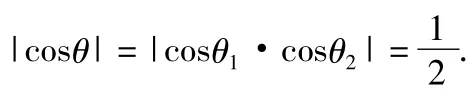
方法2以ABC1D1为一个公共底面在2侧作2个正方体，将它置于2个长方体之中，问题便迎刃而解.

考点6轨迹与实际问题

例7直线l在平面α上，直线m∥α，l，m异面，动点P在平面α上，且到直线l，m的距离相等，则点P在下列哪个轨迹上( )

A.直线 B.椭圆 C.抛物线 D.双曲线

分析本题的难点在于将空间问题转化为平面问题.如图11，设m在α上的射影为m'，作PA⊥l于点A，PC⊥m'于点C，CB⊥m于点B，联结PB，则由PA=PB，得PA2－PC2为正常数，从而点P在双曲线上.故选D.

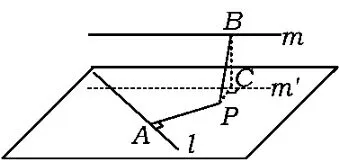
图11

考点7空间垂直与平行的证明

例8如图12，正三棱柱ABC-A1B1C1中，AB=2，AA1=4，D，E分别是AB，BB1的中点，F是棱CC1上一动点，设CF=t.

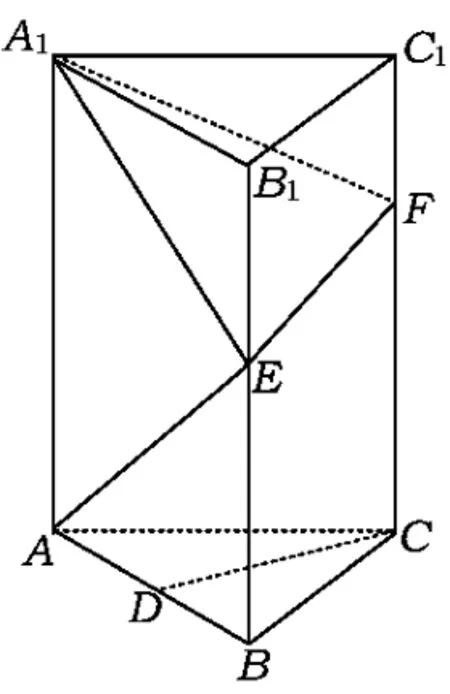
图12

1)若CD∥平面A1EF，求t的值;

2)若AE⊥平面A1EF，求t的值;

3)t为何值时，平面A1EF与底面ABC所成锐二面角最小.

解法1(综合法)

1)如图13，取A1B1的中点M，平面CDMC1交平面A1EF于FN，则FN∥CD，故t=3.

2)作AG⊥BC于点G，联结EG，故EG⊥EF，易得t=3.

3)延长A1E，A1F分别交AB，AC于点P，Q，联结PQ，作AH⊥PQ于点H，联结A1H，则∠A1HA就是平面A1EF与底面ABC所成锐二面角θ.因为，AH≤AP=4，所以

当AP⊥PQ时，θ最小，此时易得t=3.

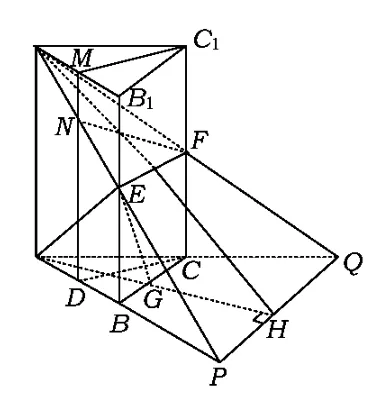
图13

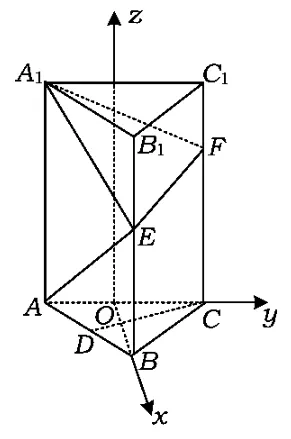
图14

解法2(向量法)分别取AC，A1C1的中点为O，O1，以O作为原点，OB，OC，OO1为x，y，z轴建立坐标系，如图14，则F(0，1，t).易得平面A1EF的一个法向量为.

3)平面ABCD的一个法向量为m=(0，0，1)，从而

当t=3时锐二面角最小.

考点8空间角与距离的计算

例9如图15，四面体ABCD中，AC⊥BC，AC⊥AD，BC=2，AC=3，AD=2，M，N分别是线段AB，CD的中点.

1)求证:AC⊥MN;

2)设二面角B-AC-D的大小为θ，二面角A-BC-D的大小为φ，若，求线段MN的长.

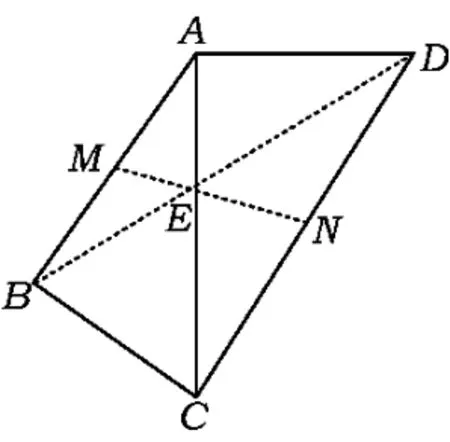
图15

图16

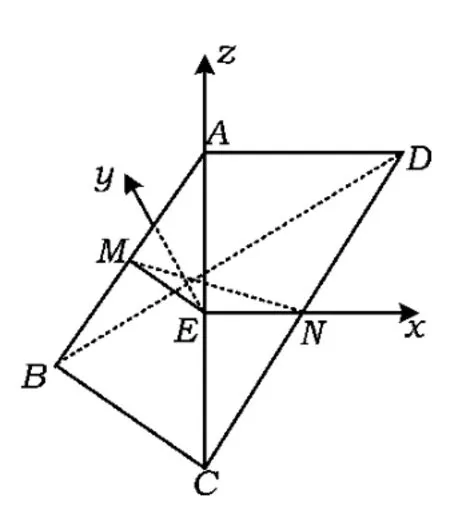
图17

解法1(综合法)

1)如图16，取AC的中点E，联结ME，NE，通过证明AC⊥平面MNE，从而AC⊥MN.

2)作CF∥AD，且CF=AD，联结DF，则DF⊥平面BCF，作FG⊥BC于点G，联结DG，则

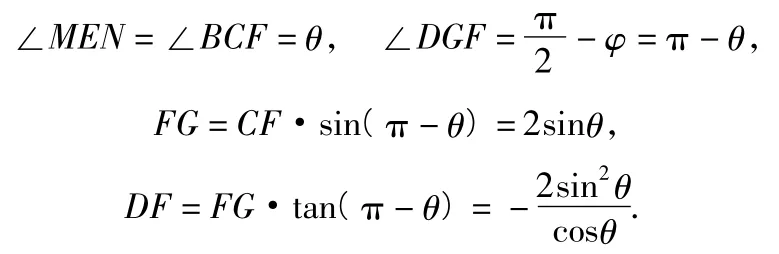
解法2(向量法)以E为原点，EN，EA分别为x轴、z轴，过点E的平面ABD的垂线为y轴，如图17建立坐标系，则M(cosθ，sinθ，0).

2)通过计算可得平面ABC的一个法向量为n1=(sinθ，－cosθ，0)，平面DBC的一个法向量为n2=(3sinθ，－3cosθ，－2sinθ)，则

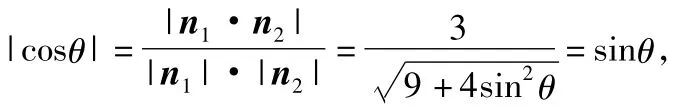
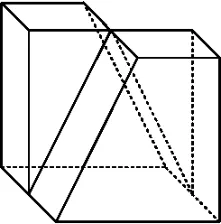
图18

4 精题集萃

1.某几何体的立体图如图18所示，该几何体的三视图不可能是( )

2.一平面α与四棱锥P-ABCD的侧棱分别交于点E，F，G，H，若EFGH为平行四边形，则底面ABCD( )

A.一定是平行四边形

B.一定是梯形

C.至少有一组对边平行

D.2组对边可以都不平行

3.如图19，ABCD-A'B'C'D'为正方体，任作平面α与对角线AC'垂直，使得α与正方体的每个面都有公共点，记这样得到的截面多边形的面积为S，周长为l，则( )

图19

A.S，l均不为定值

B.S为定值，l不为定值

C.S不为定值，l为定值

D.S，l均为定值

5.直三棱柱ABC-A1B1C1中，底面为直角三角形，∠ABC=90°，BC=CC1=1，P是BC1上一动点，则

6.如图20，现有一正三棱锥P-ABC放置在平面α上，已知它的底面边长为2，高为h，把BC靠在平面α上转动.若某个时刻它在平面α上的射影可以是等腰直角三角形，则h 的取值范围是______.

7.过正四面体A1A2A3A4的4个顶点分别作4个相互平行的平面α1，α2，α3，α4.若每相邻2个平面间的距离都为1，则该四面体的体积为_____.

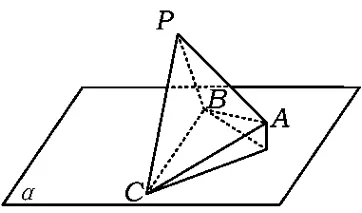
图20

8.如图21，四棱锥P-ABCD中，PA⊥平面ABCD，E为AD的中点，ABCE为菱形，∠BAD=120°，PA=AB，G，F分别是线段CE，PB上的动点，且满足.

1)求证:FG∥平面PDC;

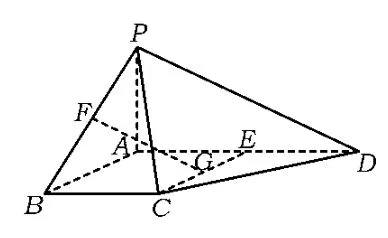
图21

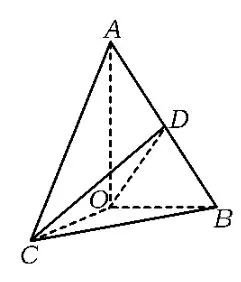
图22

1)当平面COD⊥平面AOB时，求θ的值;

10.如图23，有一边长为2的正方形纸片ABCD，E是AD边中点，将△ABE沿直线BE折起至A'BE位置，此时恰好A'E⊥A'E，点A'在底面上的射影为O.

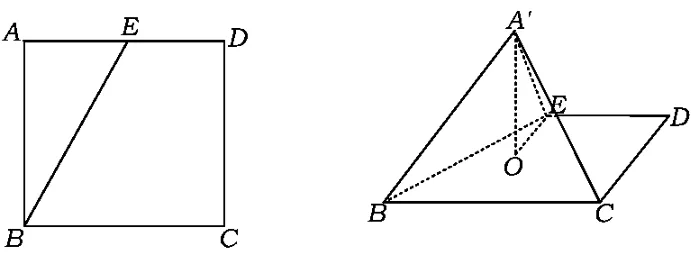
图23

1)求证:EO⊥BC;

2)求直线A'C与平面A'BE所成角的正弦值.

参考答案

1.C 2.D 3.C

8.提示:1)分别过点F，G作BC的平行线交PC，CD于点M，N，联结MN，只要证明FG∥MN.

2)由于∠BAD=120°，故建系不一定简单，因此可尝试用综合法.如图24，作FM⊥AB于点M，作MN⊥CD于点N，联结FN，则FN⊥CD，∠FNM为二面角F-CD-G的平面角.又，不妨设PA=2，则

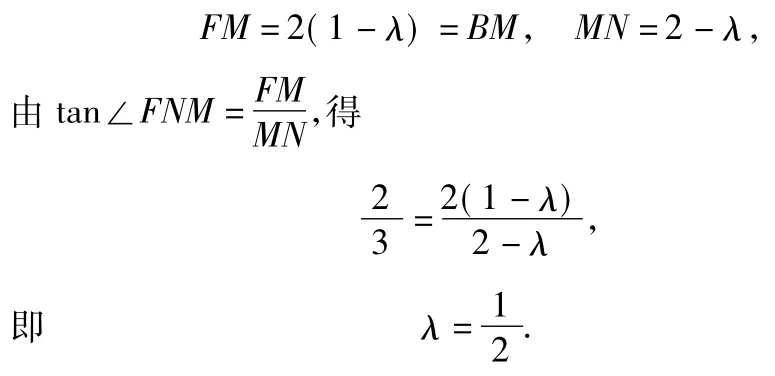
图24

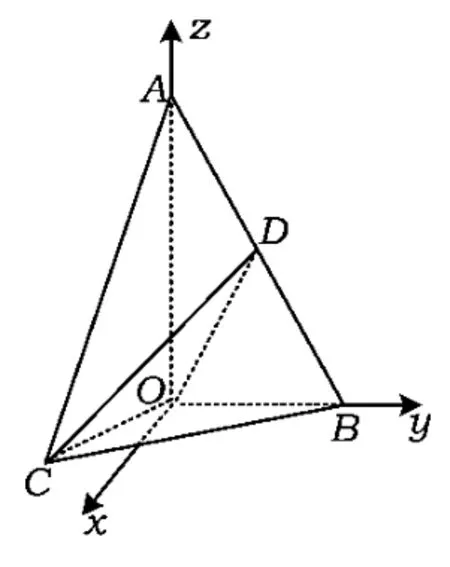
图25

9.提示:1)面面垂直通常要转化为线面垂直，故可在平面AOB内作BE⊥OD于点E，则BE⊥平面COD，故BE⊥CO.又因为CO⊥OA，所以CO⊥平面AOB，于是CO⊥BO，即θ=90°.

2)本题由于∠BOC不确定，故建系是个难点.一般可以这样建系:如图25，以O为原点，在平面OBC内垂直于OB的直线为x轴，OB，OA所在的直线分别为y轴、z轴建立空间直角坐标系O-xyz，则C(2sinθ，2cosθ，0).可求得平面COD的一个法向量，平面AOB的一个法向量为n2=(1，0，0)，设二面角C-OD-B的大小为α，当时，cosα=0;当时，，从而

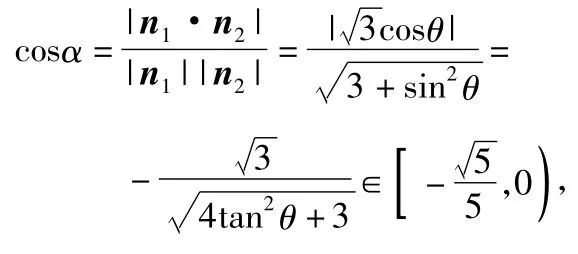
10.提示:1)因为A'E⊥A'C，A'E⊥A'B，A'C与A'B是平面A'BC内2条相交直线，所以A'E⊥平面A'BC，故A'E⊥BC.又因为A'O⊥BC，A'O与A'E是平面A'EO内2条相交直线，所以BC⊥平面A'EO，故EO⊥BC.

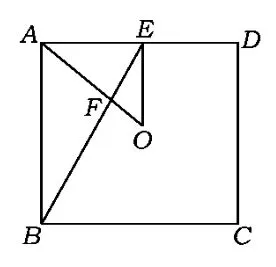
图26

图27

2)作OF⊥BE于点F，联结A'F，则A'F⊥BE，故在图26中点A，F，O共线，因此△ABE∽△EAO，于是，得得.以O为原点，过O垂直BC，CD的直线为x轴、y轴，OA'为z轴如图27建立坐标系，.在平面A'BE中，，解得平面A'BE的法向量为，－1).设直线A'C与平面A'BE所成角为θ，则