自选模块复习策略

●伊建军(杭州高级中学浙江杭州310003)

自选模块复习策略

●伊建军(杭州高级中学浙江杭州310003)

1 知识内容

2015年高考数学自选部分含“复数与导数”和“计数原理与概率”2个模块，其中复数与导数模块包含的知识内容有:导数的概念与几何意义，基本初等函数的导数公式，导数的运算法则，利用导数求函数的单调性、极值、最大(小)值，复数的概念，复数的加、减运算的几何意义，复数的四则运算.计数原理与概率模块包含的知识内容有:加法原理和乘法原理，排列与组合，二项式定理，杨辉三角与二项式系数，事件、事件的关系与运算，互斥、对立、独立事件，概率与频率，古典概型，解决简单的实际问题.

2 命题分析

复数与导数模块中导数部分主要考查基本概念与基本运算，以及导数在函数的单调性、极值、最值等方面的基本应用;复数部分主要考查复数概念和复数的运算，以及复数在复平面上表示的几何意义.计数原理与概率模块中主要考查二项式定理，二项式系数和系数的概念与计算，最基本的排列组合问题，及古典概率的理解与简单计算.在对这2个模块的考查中，也包含了一些数学思想方法的运用，如命题转换思想、分类讨论思想等.

3 典题剖析

例1设函数f(x)=6x3+3(a+2)x2+2ax.

1)若f(x)的2个极值点为x1，x2，且x1x2=1，求实数a的值.

2)是否存在实数a，使得f(x)是(－∞，+∞)上的单调函数?若存在，求出a的值;若不存在，说明理由.

分析本题包含的内容是导数在函数中的简单应用，分别是利用导数求极值及导数在函数单调性中的应用.由于极值点一定是导数等于0的点，可得x1，x2一定是导函数f'(x)=0的2个根，然后利用韦达定理即可求出a=9.

而导函数f'(x)=18x2+6(a+2)x+2a的图像是开口向上的抛物线，故当Δ≥0时，可以使得f(x)在(－∞，+∞)上单调，但此时无解，从而得到a不存在.

1)求证:函数f(x)和g(x)在(1，+∞)上都是增函数.

分析函数的单调性证明可以直接求函数的导数进行判断，因此第1)小题只需要证明导函数f'(x)≥0和g'(x)≥0在(1，+∞)上恒成立即可.

对于第2)小题，只要利用第1)小题的结论，得f(x)＞f(1)=0和g(x)＞g(1)=0在(1，+∞)上恒成立，也即x－ 1＞lnx和，可得，接下来只要把需证明的不等式转化成所得到的不等式即可.可通过换元法:设，则，即可得到证明.在该题的解题过程中，运用了一些数学方法与数学思想，如换元法、命题转换思想等，难度不大，但能考查学生的数学思维能力.

1)若复数z∈C，且z1=z2·z，求z;

分析本题是复数的基本运算问题，观察已知复数的结构形式，对简化运算步骤、提高正确率非常重要.

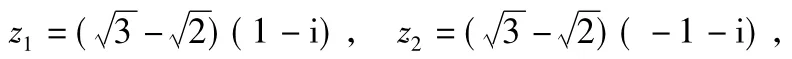
1)若复数z1－z2在复平面上对应的点落在第一象限，求实数a的取值范围;

2)若z2是实系数一元二次方程x2－6x+m=0的根，求实数m的值.

分析复数在复平面上对应的点在第一象限，即这个复数的实部与虚部均大于0.由于

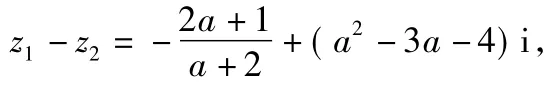
z2是实系数一元二次方程x2－6x+m=0的根，那么z2应该满足方程，代入z2，然后利用复数相等的充要条件，等式左边的实部与虚部分别等于0，可得，即此时z2为一个实数，从而求得m=8.

分析二项式定理中，二项式系数的性质是重点.本题根据二项式系数的性质可知:，代入已知条件，然后利用组合数公式即可得到m=6.

例6设(1+2x)10=(a0+a1x+a2x2+a3x3+a4x4+ a5x5)(1+x)5+(1－x)9，求a4.

分析比较等式2边的系数是解出这个问题的关键.等式2边含x项的次数从高到低逐步比较，左边二项展开式中含x10的系数为210，右边含x10的系数为a5，从而得到a5=210.左边含x9的系数为，右边含x9的系数为，即得到，可解得a4=1.

例7有一个奇数列1，3，5，7，9，…，现在进行如下分组，第1组有1个数为1，第2组有2个数为3，5，第3组有3个数为7，9，11，…，依次类推，则从第10组中随机抽取一个数恰为3的倍数的概率为______.

分析本题需要求出第10组的第1个数的值和这一组共有几个数，由于前9组共有45个数，那么第10组的第1个数是奇数列中的第46个数，这个数为91，从而可以得到第10组数中是3的倍数的数为93，99，105共3个，概率为

例8质点A位于数轴上的原点处，质点B位于数轴的x=2处，这2个质点每隔1秒就向左或向右移动1个单位，设向左移动的概率是，向右移动的概率是

1)求3秒后，质点A在点x=1处的概率;

2)求2秒后，质点A，B同时在点x=2处的概率.

“走了以后，那些个喜啊，忧啊，苦啊，乐啊，就都烟消云散了。一辈子，也就过去了。”王爷这样想着的时候，内心很平静。

分析该题需要理解的是:质点到达规定的位置后，需要进行哪几个步骤.如3秒后到达x=1处，应该是向右移了1个单位，另2次移动应该是互相抵消的，也就是向右移2个单位，向左移1个单位，从而所求的概率是

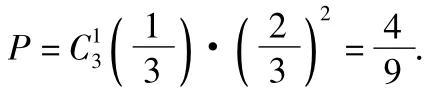
2秒后，A到达x=2处只需要向右移动2个单位，B可以向左向右各移动1次即可，于是质点A，B同时在点x=2处的概率是

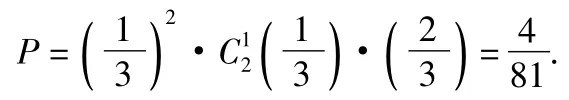
4 精题集萃

A.－2 B.－2i C.2 D.2i

2.已知(1－2x)n展开式中的奇数项的二项式系数之和为64，那么(1－2x)n(1+x)展开式中含x2项的系数为( )

A.71 B.70 C.21 D.49

3.已知函数f(x)=x(lnx－ax)有2个极值点，则实数a的取值范围是( )

A.(－∞，0)

C.(0，1)

D.(0，+∞)

4.将数1，2，3，4，5，6，7随机分成2组，使得每组至少有1个数，那么2组中各数之和相等的概率是______.

5.袋中有5张卡片，其中红色卡片3张，标号分别为1，2，3;蓝色卡片2张，标号分别为1，2;从以上5张卡片中任取2张，那么这2张卡片颜色不同且标号之和小于4的概率是_____.

6.已知a，b为正实数，函数f(x)=ax3+bx+2x在［0，1］上的最大值为4，则f(x)在［－1，0］上的最小值为______.

9.一个袋子里装有7个球，其中有红球4个，编号分别为1，2，3，4;白球3个，编号分别为2，3，4.从袋子中任取4个球(假设取到任何一个球的可能性相同).

1)求取出的4个球中，含有编号为3的球的概率;

2)求取出的4个球中，红球编号的最大值不超过2的概率.

10.若函数f(x)=x－1－alnx.

1)若a＞0，且f(x)≥－1恒成立，求a的取值范围;

2)若a＜0，且对任意x1，x2∈(0，1］，都有，求实数a的取值范围.

参考答案