分类讨论思想

●冯海容(黄岩中学浙江台州318020)

分类讨论思想

●冯海容(黄岩中学浙江台州318020)

1 知识内容

1.1 分类讨论的概念

分类讨论，就是在研究和解决数学问题时，当问题所给对象不能进行统一研究时，我们就需要根据数学对象的本质属性的相同点和不同点，将对象区分为不同种类，然后逐类进行研究和解决，最后综合各类结果得到整个问题的解决.这种思想方法，我们称之为“分类讨论思想”.分类讨论思想的本质是“化整为零，积零为整”，从而增加了题设条件的解题策略.

1.2 产生分类讨论的主要原因

1)由数学概念引起的分类讨论:如绝对值定义、等比数列的前n项和公式等;

2)由数学运算要求引起的分类讨论:如集合运算中有无空集、偶次方根非负、对数中的底数和真数的要求、不等式2边同乘一实数对不等号方向的影响等;

3)由函数的性质、定理、公式的限制引起的分类讨论;

4)由几何图形中点、线、面的相对位置不确定引起的分类讨论;

5)由参数的变化引起的分类讨论:某些含参数的问题，由于参数的取值不同会导致所得结果不同，或由于不同的参数值要运用不同的求解或证明方法;

6)其他根据实际问题具体分析进行分类讨论，如排列、组合问题、实际应用题等.

产生分类讨论的原因就是分类讨论的外在表现形式.

1.3 运用分类讨论思想解题的基本步骤

1)确定讨论对象和确定研究的全域;

2)对所讨论的问题进行合理的分类(分类时要做到不重复、不遗漏、标准统一、分层不越级)，确定分界点和分界线;

3)根据分界点和分界线逐类讨论，逐步解决;

4)归纳总结，整合得出结论.

其关键是找出分类标准，确定分界点和分界线.

1.4 合理利用其他数学思想方法和数学本质简化甚至避免分类讨论

因为分类讨论比较繁琐，特别是分类讨论中又有分类讨论时，思维严谨性要求高，容易失误，所以如何简化甚至避免分类讨论就显得非常必要.简化和避免分类讨论的方法有:

1)数形结合.利用图像、几何图形的直观性和对称特点有时可以简化甚至避开讨论.

2)变更主元.分离参数、变参置换，构造以讨论对象为变量的函数，解题时可避开讨论.

3)直接回避.如运用反证法、消参法等方法有时可以避开繁琐讨论.

4)合理运算.如利用函数奇偶性、变量的对称轮换以及公式的合理选用等有时可以简化甚至避开讨论.

2 命题分析

分类讨论思想是解决问题的一种逻辑方法，也是一种数学思想，这种思想在简化研究对象、发展思维方面起着重要作用.因此，有关分类讨论思想的数学命题在高考试题中占有重要地位，是历年高考的重点.

分类讨论思想往往结合具体的数学知识(如函数、不等式、解析几何等)进行考查;内容上五彩缤纷，各种产生分类讨论的原因均有出现;从形式上看，近几年从含一个参数的讨论慢慢转到含多个参数的讨论，从简单的分类讨论转到需运用逻辑、数形结合等数学本质的分类讨论.解决分类讨论问题首先要从落实产生分类讨论的数学知识，其次要加强运用数形结合等数学思想和数学本质来简化分类讨论.

3 典题剖析

3.1 分类讨论首先要选定讨论的对象及角度

因为分类讨论往往有多个对象(如字母、变量、函数等)，讨论的角度也多种情况，选择不同的讨论对象及角度，讨论的难易程度大不相同，所以要选定或确定讨论的对象及角度.

例1已知a＞0，b∈R，函数f(x)=4x2－1，g(x)=－2x+1.当0≤x≤1时，函数h(x)=af(x)+bg(x).

1)证明:函数h(x)的最大值为|2a－b|+a;

2)证明:h(x)+|2a－b|+a≥0.

(2012年浙江省数学高考理科试题第22题改编)

分析第1)小题的分类讨论是确定的，或利用二次函数的性质知:h(x)的最大值为max{h(1)，h(0)}，即max{3a－b，b－a}.

当2a－b≥0时，

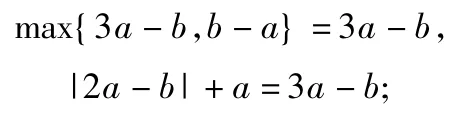
当2a－b＜0时，

故函数h(x)的最大值为|2a－b|+a.

第2)小题涉及的变量有x，a和b，关于变量x是二次，而关于变量a和b是一次，故应从a和b的角度进行分类讨论:

注当分类讨论涉及多个变量时，且对各个变量都没有特殊要求时，应根据条件选择一个变量作为分类讨论的对象.真正做到分类讨论的知识背景清楚，分类讨论的依据明白.

3.2 分类讨论的关键

分类讨论的关键是制定分类标准，确定分界点.当分类讨论需并列多次讨论时，应找出各次分类的分界点，再制定分类标准;当分类讨论需多层讨论时，应根据题意逐层讨论，或根据各层的分界点重新制定分类标准.

例2解关于x的方程:ax2－(a+1)x+a≥0，其中a∈R.

分析记f(x)=ax2－(a+1)x2+a，首先分成a＞0，a=0及a＜0这3类不同的函数问题.对于a＞0及a＜0，又要分成Δ＞0，Δ=0，Δ＜0.对于Δ＞0最后还要讨论2个根的大小，这样共3层讨论，可逐层讨论，但书写繁琐.可考虑分界点:a＞0，a=0，a＜0;或Δ＞0，Δ=0，Δ＜0;或2个根的大小比较.

1)当a＞1时，原方程的解为

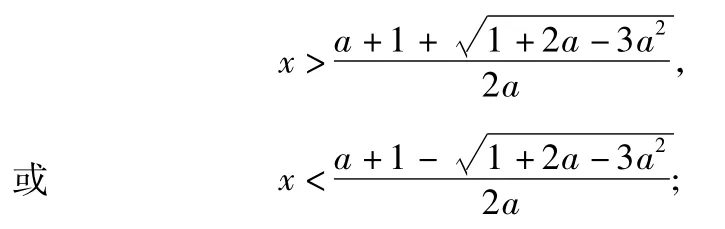
2)当a=1时，原方程的解为x≠1;

3)当0＜a＜1时，原方程无实数解;

4)当a=0时，原方程解为x＜0;

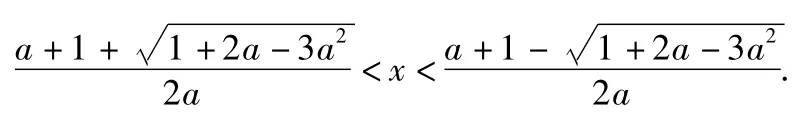
注当分类讨论涉及多层次多角度时，应根据条件综合各层次各角度分类的分界点进行扁平化处理，达到简化讨论的目的，做到不重不漏.

3.3 分类讨论应尽量利用条件缩小讨论范围

有些分类讨论问题可利用条件缩小讨论范围，不用全范围讨论，避开一些复杂的讨论问题，达到简化讨论的目的.

(2014年7月浙江省数学学业水平考试试题)

分析由题意对任意t∈［3，5］，关于x的方程f(x)=g(t)在［3，5］上至少有2个不同的解，故函数在［3，5］上不单调.而

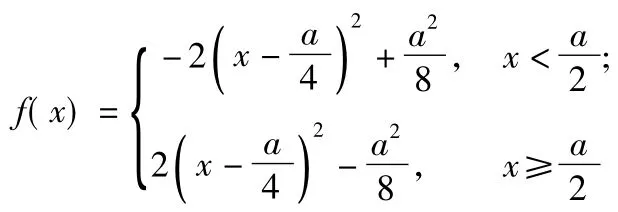
①当6＜a＜10时，对任意的t∈［3，5］关于x的方程f(x)=g(t)在［3，5］上至少有2个不同的解，从图形上知

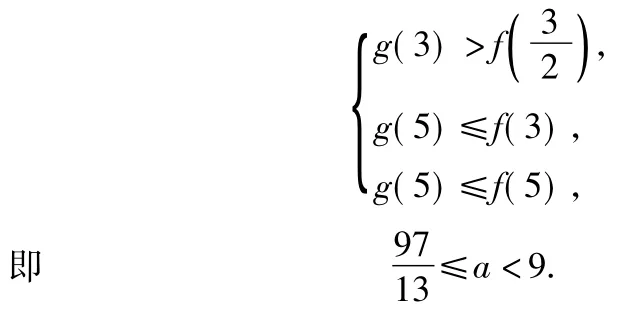
注本题虽是学业水平测试题，但无论从难度及思想上均达到了高考的要求.本题首要难点是题意的理解:对任意t∈［3，5］，关于x的方程f(x)=g(t)在［3，5］上至少有2个不同的解，再用图形得到

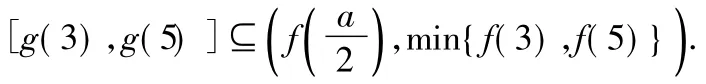
其次在具体讨论上应根据f(x)在［3，5］上不是单调函数这一必要条件缩小讨论范围，减少不必要的讨论.

3.4 分类讨论应尽量运用其他数学思想简化甚至避免分类讨论

许多分类讨论问题，若直接分类讨论则将陷入运算复杂讨论繁琐情况，若换一角度运用化归、数形结合等数学思想，则分类讨论将简化甚至避免，达到柳暗花明又一村的境界.

例4设函数f(x)=x2－ax+b(其中a，b∈R).若存在实数a，使得当x∈［0，b］时，2≤f(x)≤6恒成立，求b的最大值及此时a的值.

(2014年1月浙江省数学学业水平考试试题)

分析本题若直接分类讨论则要分成4类讨论，每类都比较繁.若从变量的作用、变量分离及数形结合角度分析本题，则讨论将大大简化.

方法1从变量作用简化

要存在实数a，则必有

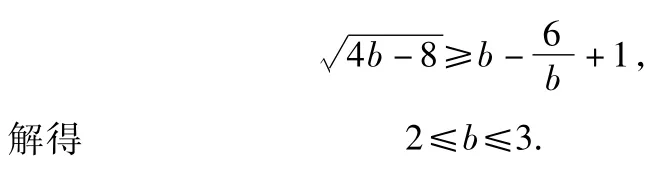
故b的最大值为3，此时a=2.

方法2从变量分离角度简化

1)当x=0时，2≤f(0)=b≤6.

①当b=6时，不存在实数a.

②当b=2时，存在实数a=2，使得2≤f(x)≤6恒成立.

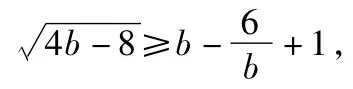
解得2＜b≤3.

故b的最大值为3，此时a=2.

方法3从数形结合思想简化

原问题转化为:存在实数a，使得当x∈［0，b)时，2－x2≤－ax+b≤6－x2恒成立，求b的最大值.即当x∈［0，b)时，直线y=－ax+b始终在函数g(x)=2－x2图像的上方，始终在函数h(x)=6－x2图像的下方.

当直线y=－ax+b与函数g(x)=2－x2图像相切时，

得切点的横坐标为

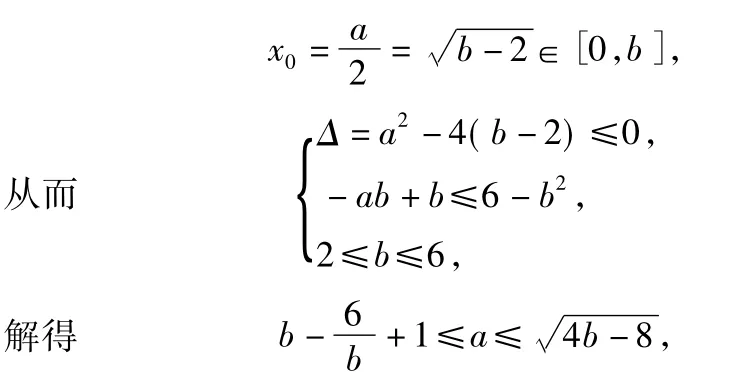
下同方法1.

例5已知函数f(x)=x3+3|x－a|(其中a∈R).设b∈R，若［f(x)+b］2≤4对x∈［－1，1］恒成立，求3a+b的取值范围.

(2014年浙江省数学高考理科试题)

分析本题是关于导数的问题，2015年浙江高考将在模块考试中考查.本题容易想到用函数的最值来讨论，对分类讨论能力、推理论证能力及运算能力要求高.从数形结合角度再看本题:

［f(x)+b］2≤4对x∈［－1，1］恒成立，即－x3－2≤3|x－a|+b≤－x3+2对x∈［－1，1］恒成立.

记g(x)=3|x－a|+b，h1(x)=－2－x3，h2(x)=2－x3.原问题等价于函数g(x)图像在［－1，1］内在h1(x)上方，在h2(x)下方(包括边界).

如图1，过函数h2(x)图像的2个端点A(－1，3)，B(1，1)分别为直线l1:y=－3x和l2:y=3x－2.经检验直线l1与函数h2(x)的图像相切于点A，与函数h1(x)图像相切于点D.

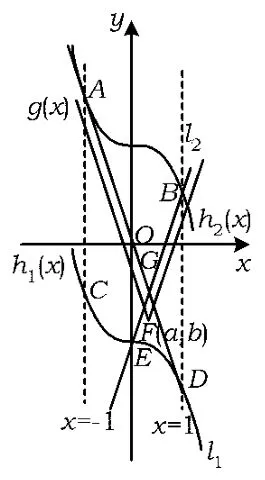
图1

要使得函数g(x)图像在［－1，1］内在h2(x)下方，只要函数g(x)图像的顶点F(a，b)既在直线l1的下方又在直线l2的下方(包括边界).

要使得函数g(x)图像在［－1，1］内在h1(x)上方，只要函数g(x)图像的顶点F(a，b)既在直线l1的上方或在曲线段CED上方(包括边界).

综上，函数g(x)图像的顶点F(a，b)在曲线段CED，l1，l2所围成的区域内(包括边界)或在射线FD上时即可，从而－2≤3a+b≤0.

注如何简化分类讨论是分类讨论问题关键所在，直接分类讨论入口宽但要求高得分低，要多利用其他思想方法简化分类讨论.

4 精题集萃

A.λ＜3 B.λ＞－2

C.－2＜λ＜3 D.－2＜λ＜2

A.无论a为何值，均有2个零点

B.无论a为何值，均有4个零点

C.当a＞0时有4个零点，当a＜0时有1个零点

D.当a＞0时有3个零点，当a＜0时有2个零点

3.设函数f(x)=(x－a－1)|x－2a|(其中a∈R)，若函数f(x)在［－2，0］上的最小值为－1，则实数a的值为( )

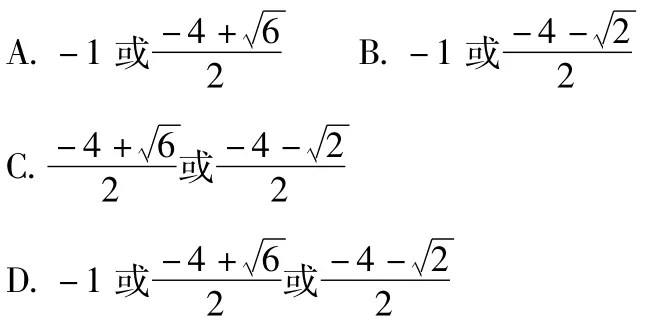
4.与圆(x+2)2+y2=1相切，且在2个坐标轴上截距相等的直线方程为________.

6.已知函数f(x)=loga(2－ax)(其中a∈R)在［0，1］上是减函数，则实数a 的取值范围是______.

7.若四面体各棱长是1或2，且该四面体不是正四面体，则该四面体的体积为______.

8.若数列{an+2n}是首项为3、公差为3的等差数列，求数列{|an|}的前n项和为Sn.

9.设函数f(x)=x2+a2+|x－a|(其中a∈R).

1)求函数f(x)的最值;

2)若不等式f(x)≥4恒成立，求实数a的取值范围.

1)若函数f(x)在［2，+∞)上单调递增，求实数a的最小值;

参考答案