高考解答题的剖析

●胡水林王峥(元济高级中学浙江海盐314300)

高考解答题的剖析

●胡水林王峥(元济高级中学浙江海盐314300)

1 知识内容

数学高考解答题可分为低档题、中档题和高档题3个档次.低档题主要考查基础知识、基本方法和基本技能;中档题还要考查数学思想和运算能力、思维能力、整合与转化能力、空间想象能力;高档题还要考查灵活运用数学知识的能力及分析问题和解决问题的能力.

浙江省从2006级学生开始推行新课程改革，2009年为新高考的第一年.纵观浙江省新高考6年的数学解答题，每年5个大题6种题型，相对较稳定.其中立体几何、解析几何、函数与导数题型每年必考，解三角形题型考过5次，离散型概率题考过4次，数列题型考过3次.随着2012年深化课程改革，高中数学教学内容也作了调整.其中，概率和函数导数题型不列入必考范围，只剩下5种题型，而每种题型前几年均已考过.因此，2015年高考的解答题应该是5个大题，题型为解三角形、数列、立体几何、解析几何、函数等.

2 命题分析

2.1 三角遵循一个“稳”字

三角大题预计以稳定为主，不会有大变化，仍以三角函数图像、性质、化简、恒等变形、运算、正(余)弦定理在解三角形的应用为主.在复习时只要注意仔细计算，熟练掌握公式自然可以手到擒来.

2.2 数列递推强调一个“律”字

数列重回大题舞台，如果数列放在大题的第2题(如2011年、2014年浙江省数学高考试题)，相信难度不会很大.在复习过程中，注意以等差、等比数列为载体，以数列通项与求和为主体，同时注意数列与函数的关系，突出基础，注意常规，通过对类型问题的学习，掌握通性通法，才能以不变应万变.如数列放在最后作压轴题(如2014年浙江省测试卷)，相信难度较大，将会与函数、不等式等知识点融汇，提升难度.

2.3 立体几何用好一个“动”字

立体几何大题的常见考点还在于直线、平面的位置关系，3种角度的大小，确定动点位置等问题.从近几年高考命题情况看，题目背景往往设计成线面的平行或垂直、3种角、平面图形折叠、旋转或点在边上移动等动态情形.无论使用纯几何方法还是空间向量计算方法都能解决问题，但向量方法的优势不再明显.特别是在无法直接建系的情况下，往往需要用几何方法证明建系的合理性.

2.4 解析几何突出一个“质”字

解析几何大题一般有2个小题，第1小题求圆锥曲线方程，属于简单题，但2014年也有一定的难度.第2小题涉及直线与圆锥曲线位置关系等综合运用问题，具有一定难度，学生们往往比较惧怕，失分颇多.在复习时应注意通性通法的落实，提高综合应用知识的能力.同时，解析几何大题体现了用代数方法解决几何问题的本质，因此，运算量相对较大，要特别注意步骤的规范性和条理性.

2.5 初等函数显现一个“活”字

初等函数知识点众多，考查形式变化多端，是最难预测和准备的一道大题.要想拿高分，更多的是临场的见招拆招，平时要对函数单调性与最值、参数取值范围、函数交点与方程根的个数问题、任意性与存在性问题等一系列常见问题研究透彻，考场中比较试题与哪类问题更接近，就能有针对性地解题.此类大题综合性很强，常常会牵涉到不等式、数列等各类知识点的交集，要引起足够的重视.

3 典题剖析

例1某实验室一天的温度(单位:℃)随时间t(单位: h)的变化近似满足函数关系:

1)求实验室这一天的最大温差;

2)若要求实验室温度不高于11℃，则在哪段时间实验室需要降温?

(2014年湖北省数学高考理科试题)

分析本题是三角函数的实际运用问题.第1)小题可以通过两角和的正弦公式把f(t)变成

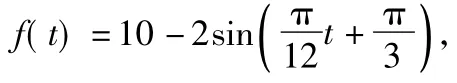
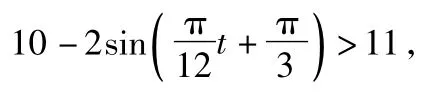
得出t的取值范围10＜t＜18，从而得到结论.

随着离散型概率应用题的退出，考查三角函数实际运用问题的可能性越来越大，应在复习时引起足够的重视.

题型解析以三角函数的实际运用问题为切入点，运用辅助角公式等简化得到三角函数的一般式，是常见的一种问题形式.三角函数在固定区间上求值域问题要由内而外，层层推得，切不可操之过急.函数图像的平移要谨记变换仅对x进行.

例2在△ABC中，内角A，B，C所对的边分别为a，b， c，已知a≠b，

1)求角C的大小;

(2014年浙江省数学高考理科试题)

分析本题主要考查诱导公式、两角和差公式、二倍角公式、正(余)弦定理、三角形面积公式等基础知识，同时考查运算求解能力.

1)解法1由已知条件，可以利用降幂式进行降幂及二倍角变形得

移项整理，再利用两角和与差的三角函数关系，得

解法2利用变角策略，先将

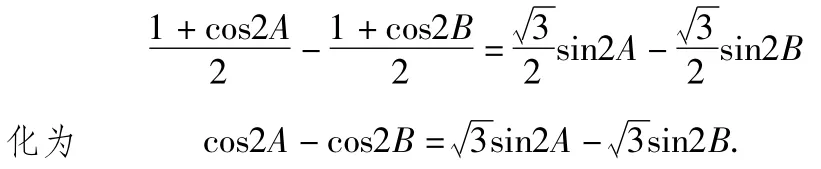
再将2A=(A+B)+(A－B)和2B=(A+B)－(A－B)利用两角和差的正弦、余弦公式展开，整理可得

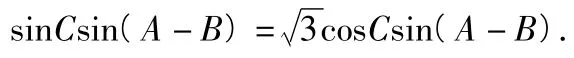
由于a≠b，且A，B是三角形的内角，则

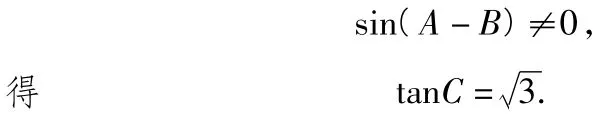
解法3利用正、余弦定理进行边角转化策略，可以先通过平方和关系，将原式化为

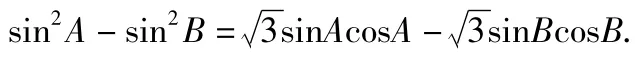
设△ABC的外接圆半径为R，根据正、余弦定理可知

因为a≠b，所以

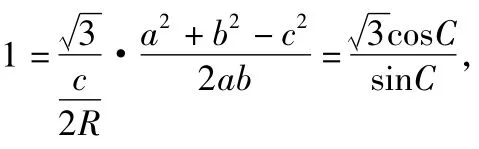
2)解利用正弦定理

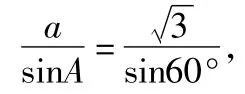
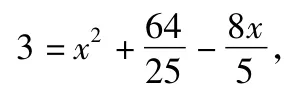
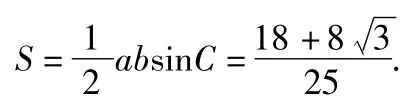
剖析技巧三角函数需仔细，常规运算是主题，倍角诱导二合一，两角和差正反记.边长面积三角形，用好正余弦定理，有时向量来联姻，考点还在数量积.

例3如图1，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，

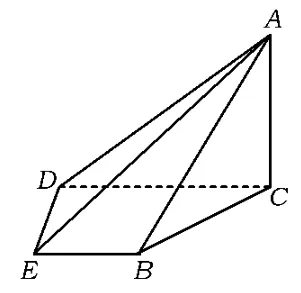
图1

图2

1)证明:DE⊥平面ACD.

2)求二面角B-AD-E的大小.

(2014年浙江省数学高考理科试题)

分析1)本题是证明线面垂直的问题，先证线线垂直，即证线和平面内2条相交直线垂直.由已知可得DE⊥DC，只需证明AC⊥DE或AD⊥DE.只需证明AC⊥BC，就得

2)本题是求二面角的大小问题，可用传统方法，也可用向量法.用传统方法，关键是找二面角的平面角，可利用三垂线定理来找，但本题不存在利用三垂线定理的条件，需转化条件.

解法1(等价转化策略)由第1)小题可知二面角E-AD-C的大小为，故可以先求二面角B-AD-C.如图2，可以利用三垂线定理来找二面角的平面角，易得∠BGF为二面角B-AD-C的平面角，解Rt△BGF，得，从而二面角B-AD-E的大小为.

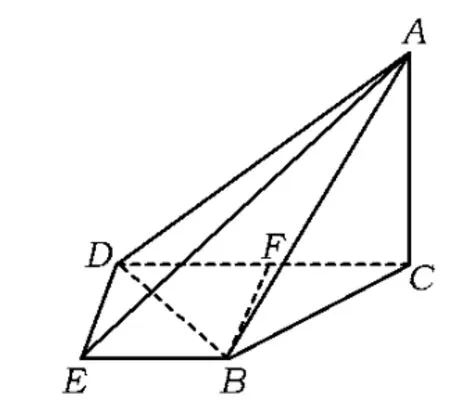
图3

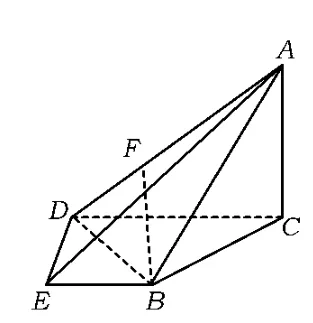
图4

解法2(转化为定义策略)设点B到平面ADE的距离为h，点B到直线AD的距离为l.设二面角B-AD-E的平面角大小为θ，于是只要求出h和l，则即可.如图3，作BF∥DE，联结BD，l可在Rt△ABD内求得，h即为:点B到平面ADE的距离h等于点F到平面ADE的距离，从而h=DF·sin∠ADC.

解法3(几何向量法)如图4，过点B作BF⊥AD，垂足为F.设二面角B-AD-E的大小为θ，则，由，平方后化简即可得到θ的值.

解法4(利用垂面法)作BF⊥AD，与AD交于点F，过点F在平面ADE内作FG∥DE交AE于点G.在Rt△AED中，求得，在Rt△ABD中，求得，从而.在△ABE和△ABG中，利用余弦定理分别可得

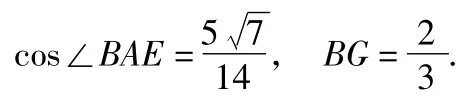
在△BFG中，

剖析技巧立体几何搞“线面”，平行垂直正流行;直角坐标不易建，几何方法需提防;折叠需看两张图，旋转基本量不变;三种角度莫混淆，锐角钝角辨别清.

例4如图5，点P(0，－1)是椭圆C1:(其中a＞b＞0)的一个顶点，C1的长轴是圆C2:x2+y2=4的直径.l1，l2是过点P且互相垂直的2条直线，其中l2交圆C2于2个点，l2交椭圆C1于另一点D.

1)求椭圆C1的方程;

2)求△ABD面积取最大值时直线l1的方程.

(2013年浙江省数学高考理科试题)

分析1)由已知得到，椭圆的方程为

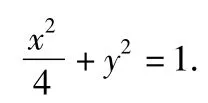
图5

2)解法1(通性通法)本题是一组互相垂直的动直线与2条定圆锥曲线相交，得到动三角形的面积最值问题.因为直线l1⊥l2，且都过点P(0，－1)，所以设直线l1:y=kx－1，直线l2:，求出圆心到直线l1的距离，再用勾股定理求出弦由直线l2与椭圆联立方程组，利用韦达定理、弦长公式求出，从而，再利用基本不等式，求出最大值，并求出等号成立的条件:，进而求直线l1.

解法2引入直线的参数方程:lAB:x=tcosα，y=－1+ tsinα，代入圆方程，求出|AB|的长.设lPD:x=－tsinα，y=－1+tcosα代入椭圆方程，求出|PD|的长，将S△ABD的面积表示成α的三角函数，再求出最值.

解法3利用三角代换.设椭圆上点D的坐标为(2cosα，sinα)，则直线AB的方程为

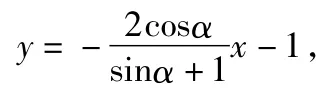
然后求出|AB|的长，再求出|PD|的长，将S△ABD表示成α的三角函数，再求出最值.

剖析技巧解析几何很重要，高考答题压轴考;取值范围点坐标，定点定值轮番俏;常规方法巧应对，两式联立不可少;韦达定理判别式，弦长公式三法宝;若能利用几何图，数形结合是本质.

例5已知函数f(x)=x2－1，g(x)=a|x－1|.

1)若关于x的方程|f(x)|=g(x)只有1个实数解，求实数a的取值范围;

2)若当x∈R时，不等式f(x)≥g(x)恒成立，求实数a的取值范围;

3)求函数h(x)=|f(x)|+g(x)在区间［－2，2］上的最大值.

分析1)本题是考查含绝对值方程有唯一解的问题.利用移项，因式分解可得|x－1|(|x+1|－a)=0只有唯一解，从而求出结论a＜0.

2)本题是不等式的恒成立问题.利用等价转换思想，通过分类讨论、分离参变量的方法将对x≠1恒成立问题转化为求函数(其中x≠1)的最值问题，从而求得a≤－2.

3)本题是含绝对值函数的最值问题.利用分类讨论思想，将含绝对值函数转化为含参的二次分段函数，最后求含参分段函数的最值问题.

因为h(x)=|f(x)|+g(x)，x∈［－2，2］，所以

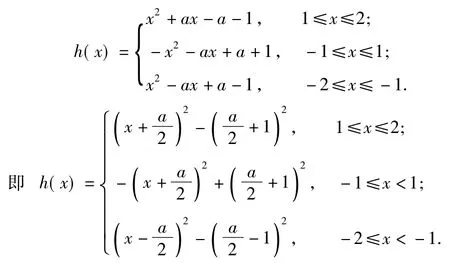
下面进行分类讨论:

h(x)max=max{h(－2)，h(2)}=max{3+3a，a+3}.因为a≥2，所以3+3a＞3+a，于是

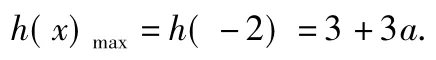
图6

图7

当0＜a＜2时，

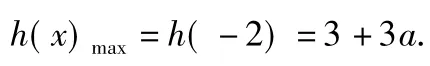
当－2≤a＜0时，

因为－3≤a＜－2，所以3+a＞3+3a，故

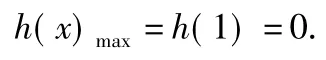
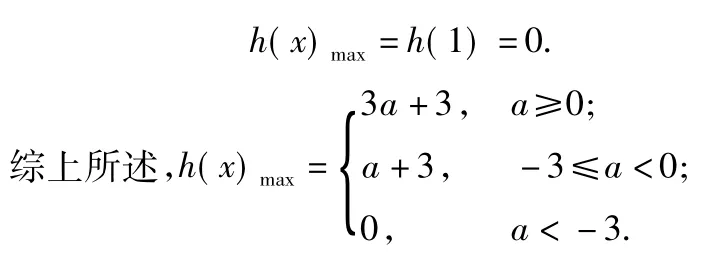
剖析技巧函数问题千千万，图像成真是根本;指对二次绝对式，当下最潮是混搭;一个绝对遇棘手，梅开二度显真章;常规套路平时记，灵活运用巧拆招.

例6如图8，已知曲线C:y=x2(其中0≤x≤1)，O(0，0)，Q(1，0)，R(1，1).

取线段OQ的中点A1，过点A1作x轴的垂线交曲线C于点P1，过点P1作y轴的垂线交RQ于点B1，记a1为矩形A1P1B1Q的面积.

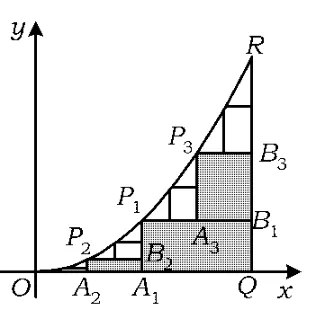
图8

分别取线段OA1，P1B1的中点A2，A3，过点A2，A3分别作x轴的垂线交曲线C于点P2，P3，过点P2，P3分别作y轴的垂线交A1P1，RB1于点B2，B3，记a2为2个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.

以此类推，记an为2n－1个矩形面积之和，从而得数列{an}，设这个数列的前n项和为Sn.

1)求a2与an;

2)求Sn，并证明:.

分析本题是函数图像下构建数列递推公式和数列求和问题.

1)由P1求得a1;由点P2，P3的坐标求出

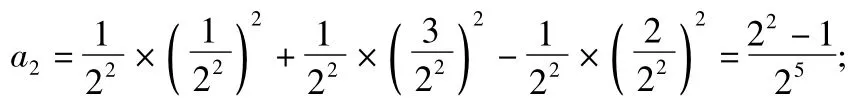
再由点P4，P5，P6，P7的坐标求出

由此归纳，对于任意的n∈N*，有

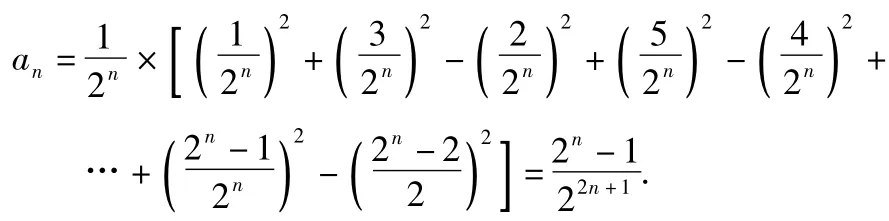
2)由分组等比数列求和公式，即可得证.

剖析技巧数列重现大题时，回归之年难度低;等差等比是基础，通项求和记心间;错位相减五步走，常见递推胸中藏;数列函数本一家，灵活掌握不怕难.

4 精题集萃

1)求函数f(x)的最大值;

2.在△ABC中，内角A，B，C所对的边分别为a，b，c，已知a≠b，

1)求角C的大小;

(2014年浙江省数学高考理科试题)

3.已知数列{an}和{bn}满足(其中n∈N*)，若{an}为等比数列，且a1=2，b3=6+b2.

1)求an与bn.

①求Sn;

②求正整数k，使得对任意n∈N*，均有Sk≥Sn.

(2014年浙江省数学高考理科试题)

4.如图9，在矩形ABCD中，点E，F分别在线段AB，AD上，.沿直线EF将△AEF翻折成△A'EF，使平面A'EF⊥平面BEF.

1)求二面角A'-FD-C的余弦值;

2)点M，N分别在线段FD，BC上，若沿直线MN将四边形MNCD向上翻折，使点C与点A'重合，求线段FM的长.

(2013年浙江省数学高考理科试题)

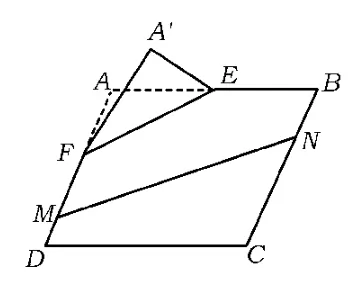
图9

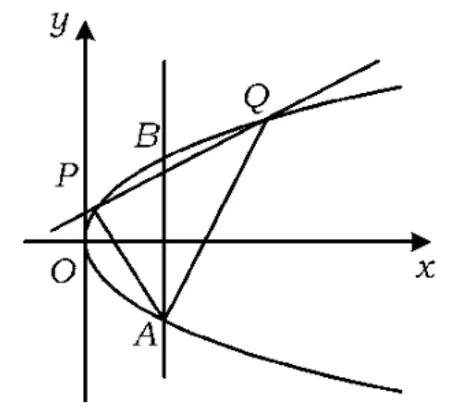
图10

5.如图10，2条相交线段AB，PQ的4个端点都在抛物线y2=x上，其中直线AB的方程为x=m，直线PB的方程为

1)若n=0，∠BAP=∠BAQ，求m的值;

2)探究:是否存在常数m，当n变化时，恒有∠BAP=∠BAQ?

6.已知函数f(x)=x|x－a|－b，其中a，b∈R.

2)当x∈［0，1］时，f(x)＜0恒成立，求b的取值范围(用a表示).

参考答案

3.1)an=2n，bn=n(1+n).

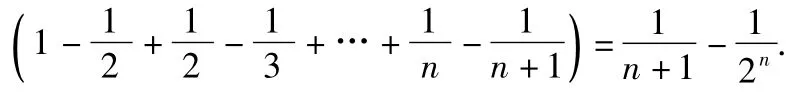
由于x+1增长速度低于2x，故只要观察前几项即可得到k.由

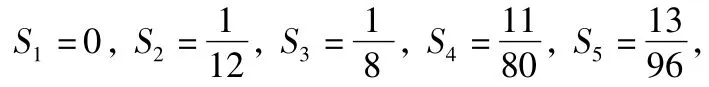
可得k=4.

4.解1)取线段EF的中点H，AF的中点G，联结A'G，A'H，GH.由A'E=A'F及H是EF的中点，知A'H⊥EF.因为平面A'EF⊥平面BEF，所以A'H⊥平面BEF，又因为AF⊂平面BEF，所以A'H⊥AF.由G，H是AF，EF的中点，易知GH∥AB，从而GH⊥AF，于是AF⊥面A'GH，故∠A'GH为二面角A'-DH-C的平面角.在Rt△A'GH中，，GH=2，，从而，故二面角A'-DF-C的余弦值为

2)设FM=x，因为翻折后，点C与点A'重合，所以CM=A'M.而

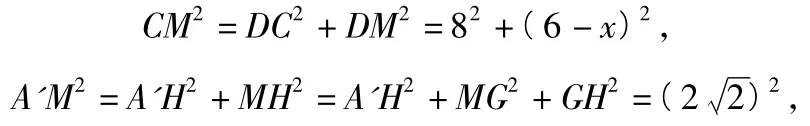
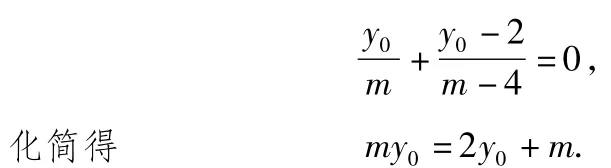
因为AB平分∠PAQ，所以m=4不合题意，故m=1.

2)设P(x1，y1)，Q(x2，y2)，由得

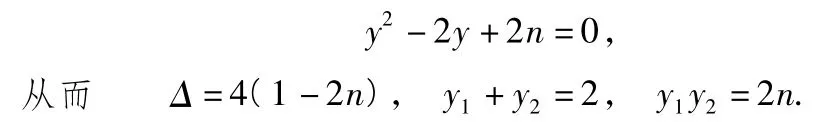
若存在常数m，当n变化时，恒有∠BAP=∠BAQ，则只可能m=1.

因此，存在常数m=1，当n变化时，恒有∠BAP=∠BAQ.

6.解1)因为

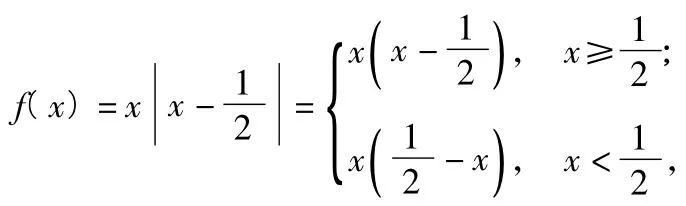
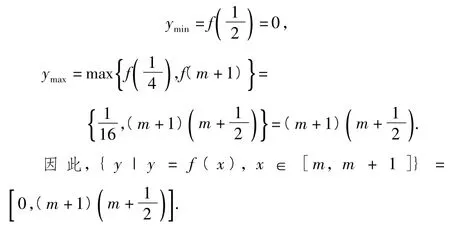
2)因为f(x)＜0，所以

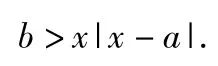
令g(x)=x|x－a|，从而x∈［0，1］，f(x)＜0恒成立，即

当a≤0时，g(x)=x(x－a)，其在［0，1］上递增，故b＞1－a.

当0＜a＜1时，