高考选择题解题策略
2015-12-07熊丰羽宁波中学浙江宁波315040
●熊丰羽(宁波中学浙江宁波315040)
高考选择题解题策略
●熊丰羽(宁波中学浙江宁波315040)
1 题型解读
选择题是高考的三大题型之一.纵观浙江省近10年数学高考试题,选择题的题量和分值都十分固定,题量占到全卷近,分值占,从这2个比例可以看出选择题的重要性.同时,选择题又是学生考试过程中要过的第一道关,学生对选择题的得分期望往往也大于填空题和解答题.因此,能否解好选择题,往往是高考成功的关键.
解好选择题,除了准确之外,还要求迅速.在高考中,平均每道选择题要在3分钟内解完.完成这个要求对于选择题的前几题来说问题不大,但对最后2道题而言就比较困难.经常有学生在最后2道选择题上花了20分钟甚至更多的时间而导致“超时失分”.因此,解好选择题除了需要扎实的基础功外,还需要一定的策略和技巧.
选择题不同于解答题,它不需要写解答过程,这就允许进行合理地“猜想”.选择题也不同于填空题,它提供了4个选择项,其中必有1个正确答案.因此,在解答选择题时应该突出一个“选”字,可以充分利用题干和选择支提供的信息.一般来说,选择题的解答策略有2种:1)直接法,即从题干出发,探求结果,一般适用于题号在前1~5的题目;2)间接法,即从选项出发,或者将题干与选项联合考察而得到结果.间接法中常见的方法包括数形结合、特值代验、逻辑排除、极端分析等等.下面主要就间接法中常见的几种方法分别举例说明之.
2 典题分析
2.1 数形结合
例1设0<x1<x2<π,则的大小关系是( )
A.a>b B.a<b
C.a=b D.无法确定
评析数形结合作为一种解题策略,并非为选择题所专有,它是一种广泛应用的数学思想和解题策略.数形结合包括“以形助数”和“以数辅形”,在选择题中更常见的是前一种策略.运用这种策略的前提是:熟悉常见的函数、方程、不等式所对应的图形.
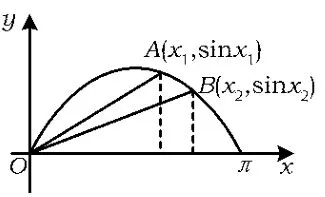
图1
本题也可以利用特殊值代入,但是由于选项D的存在,用特值法有一定风险.
例2已知函数f(x)是定义在R上的奇函数,当x≥0时,
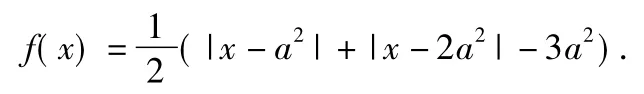
若对任意x∈R,f(x-1)≤f(x),则实数a的取值范围为( )

分析本题如果直接求解,则十分复杂.可以考虑作出函数y=f(x)的图像,通过比较y=f(x-1)和y=f(x)的图像求解.因为当x≥0时,

所以当0≤x≤a2时,
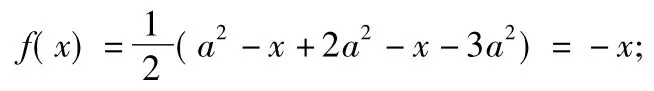
当a2<x<2a2时,

当x≥2a2时,

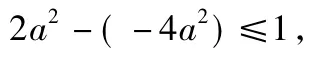
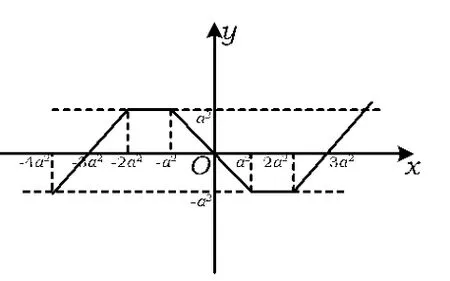
图2
2.2 特值法
例3已知函数f(x)=ax3+bx2+cx+d(其中a,b,c,d∈R)的图像如图3所示,则b的取值范围是( )
A.(-∞,0) B.(0,1)
C.(1,2) D.(2,+∞)
分析根据图像,不妨设函数

此时a=1,b=-3,c=2,d=0.故选A.
评析这类题目如果脚踏实地地求解,不仅运算量大,而且极易出错,而利用图像提供的信息,构造特例,既快又准.当然,有时可能构造1个特例只能排除1个或2个选项,此时可以考虑多取几次特值.但要特别注意,所选的特殊值必须满足已知条件.常用的特例有特殊值、特殊函数,特殊数列、特殊图形、特殊点等.特值法一般适用于解答“对某种关系恒成立”、以全称命题形式出现的题目.

图3
例4如图4,在空间中,过点A作平面π的垂线,垂足为B,记B=fπ(A).设α,β是2个不同的平面,对空间任意一点P,Q1=fβ[fα(P)],Q2=fα[fβ(P)],恒有PQ1=PQ2,则( )

图4
A.平面α与平面β垂直
B.平面α与平面β所成的(锐)二面角为45°
C.平面α与平面β平行
D.平面α与平面β所成的(锐)二面角为60°
取特例,令AD1和A1D的交点为P,取2个相邻面ADD1A1和A1B1BA检验选项A可以成立;取2个相对的面AD1DA1和B1C1CB检验选项C显然不成立,面AB1C1D与面AD1DA1所成角为60°,此时若面AB1C1D为α,面AD1DA1为β,则,同理,若另构造一个平面与面ADD1A1所成角为45°,则.故选A.
评析不满足恒成立有2种情况:一是恒不成立,一种是不恒成立.在取特例时要特别注意后面这种情况.本题中检验选项C时,如果取相对面ABCD和A1B1C1D1,则选项C可以成立.因此举特例可以成立不一定就是答案.本题中要解决这个问题,可以将点P取得更平凡一点,比如说线段A1A的四等分点,或者多取几种情况验证.
例5设S,T是2个非空子集,如果存在一个从S到T的函数y=f(x)满足:1)T={f(x)|x∈S};2)对任意x1,x2∈S,当x1<x2时,恒有f(x1)<f(x2),那么称这2个集合“保序同构”.以下集合对不是“保序同构”的是( )
A.A=N*,B=N
B.A={x|-1≤x≤3},B={x|x=-8或0<x≤10}
C.A={x|0<x<1},B=R
D.A=Z,B=Q
分析本题的背景知识是集合的势,了解高等数学知识,很容易选出答案为D.对学生而言,比较合适的方法是利用题目所提供的条件构造特殊函数,逐一验证.函数f(x)为定义域S上的增函数,值域为T.构造函数f(x)=x-1,x∈N*,则f(x)的值域为N,且为增函数,故选项A正确;构造函数
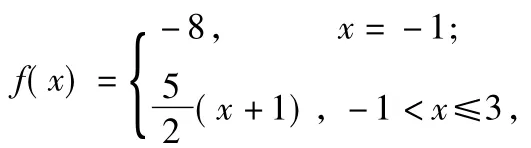
满足题设条件,故选项B正确;构造函数

满足题设条件,故选项C正确.答案为D.
2.3 排除法
例6设△ABC,P0是边AB上一定点,满足,且对于边AB上任一点P,恒有,则( )
A.∠ABC=90° B.∠BAC=90°
C.AB=AC D.AC=BC
分析本题直接做较难,学生往往无从下手,而分析选项后可以发现,4种情况都比较特殊,因此我们可以对每种情况逐一验证排除错误选项.对于选项A,由向量数量积的几何意义可知:,不可能当时最小,同理对选项B,
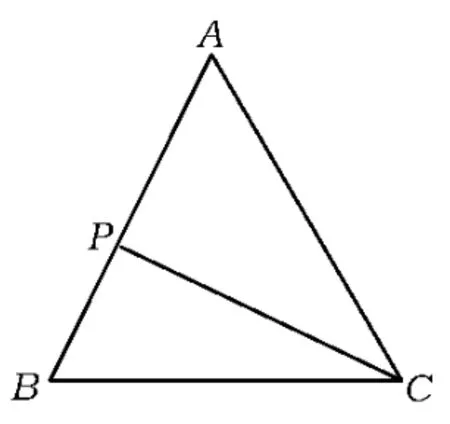
图5
评析排除法适用于不易直接求解的选择题,特别是条件探索性的题目,即结论已知,让我们探索结论成立的条件.这类题目选择支所给的往往是几种特殊情况,我们可以从特殊情况出发,再结合题目中的条件,进行逐一排除.排除法可以分步进行,即先根据某些条件排除明显不成立的选项,再根据另一些条件在缩小的范围内找出矛盾,直至选出正确答案.排除法也常常与特值法、图像法结合使用.
A.min{|a+b|,|a-b|}≤min{|a|,|b|}
B.min{|a+b|,|a-b|}≥min{|a|,|b|}
C.max{|a+b|2,|a-b|2}≤|a|2+|b|2
D.max{|a+b|2,|a-b|2}≥|a|2+|b|2
分析选项A和B比较容易排除.对于选项A,当a=0,b≠0时,不等式不成立;对于选项B,当a=b≠0时,不等式不成立;对于选项C,D,如图6,设,构造▱OACB,根据平行四边形法则,∠AOB与∠OBC至少有1个大于或等于90°,根据余弦定理知
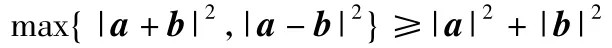

图6
成立.故选D.
2.4 极端分析法
例8已知点A(-1,0),B(1,0),C(0,1),直线y=ax+b(其中a>0)将△ABC分割为面积相等的2个部分,则b的取值范围是( )

分析可以利用极限位置和特值法.由于a>0,可以先考虑当a=0时的情况,即直线与边AB平行,易得;考虑另一种极限位置即斜率不存在,CO即所求,如图7,将CO顺时针旋转,与y轴交于点P,与BC,AB分别交于点E,F,则△CEP的面积必须等于△OFP的面积.由面积公式可知,点P的纵坐标必须小于,因此答案为B.
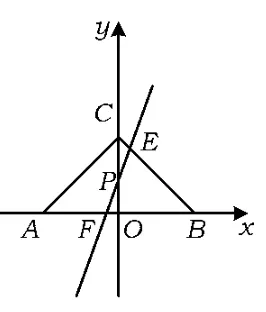
图7
评析极限分析法一般适用于求取值范围或运动变化类的问题,利用变化过程中的极端情况,化动为静,简化问题.当然,如何取极端情况是一个难点,解题中可以多考虑几种特殊的位置进行比较.
以上各种方法在实战中需灵活应用,有时要多法并用.“冰冻三尺,非一日之寒”,要让学生能熟练掌握解选择题的各种技巧:首先应鼓励学生解选择题时“小题小做,多想少算”;其次要引导学生有意识地积累一些经典题型,分门别类,经常玩味,以提高自己在这方面的能力.
4 精题集萃
1.设f(x)=|3x-1|,a>b>c且f(c)>f(a)>f(b),则下列关系中一定成立的是( )
A.3c>3bB.3b>3a
C.3c+3a>2 D.3c+3a<2

3.已知边长都为1的正方形ABCD与DCFE所在的平面互相垂直,点P,Q分别是线段BC,DE上的动点(包括端点),设线段PQ中点的轨迹为R,则R的长度为( )

5.已知函数f(x)=cosxsin2x,下列结论中错误的是( )
A.y=f(x)的图像关于点(π,0)中心对称
D.f(x)既是奇函数,又是周期函数
6.已知等比数列{an}的公比为q,记bn=am(n-1)+1+ am(n-1)+2+…+am(n-1)+m,cn=am(n-1)+1·am(n-1)+2·…· am(n-1)+m(其中m,n∈N*),则以下结论一定正确的是( )
A.数列{bn}为等差数列,公差为qm
B.数列{bn}为等比数列,公比为q2m
C.数列{cn}为等比数列,公比为qm2
D.数列{cn}为等比数列,公比为qmm
7.有4根长都为2的直铁条,若再选2根长都为a的直铁条,使这6根铁条端点处相连能够焊接成一个三棱锥形的铁架,则的取值范围是( )
8.在△ABC中,已知∠BAC的平分线交BC于点M,且BM∶MC=2∶3.若∠AMB=60°,则==( )


参考答案
1.D 2.C 3.C 4.A 5.C 6.C 7.A 8.B 9.D
