组合式螺旋桨重心误差评价与修正

梁延德　孙捷夫　何福本　鲁亚恒

大连理工大学,大连,116024

组合式螺旋桨重心误差评价与修正

梁延德孙捷夫何福本鲁亚恒

大连理工大学,大连,116024

由于桨叶在成形加工过程中受制造精度、材料缺陷及装配误差等非设计因素的影响，导致组合式螺旋桨的实际重心位置与理论设计重心位置不一致，对其力学性能会产生不良影响，因此需要对相关桨叶进行重心误差评价和去重处理以修正重心误差。提出了重心最小包容球和重心公差球的概念和算法，并以此为依据判断桨叶是否需要进行重心修正。同时根据重心组合原理，分别以修正质量最小和桨叶重心离散程度最小为标准，提出了相应的修正方案，并利用理论分析和仿真实验相结合的方法验证了方案的可行性。

组合式螺旋桨;最小包容球;重心公差球;最小修正质量;重心离散程度

0　引言

组合式螺旋桨是由同种规格的多个桨叶通过焊接或铆接的方式组装而成的螺旋桨整体。桨叶的加工制造过程是先将铸造好的桨叶毛坯件在普通机床上进行粗加工，然后通过数控机床进行精加工以及后期人工修整，但在实际制造过程中,由于存在加工精度以及装配误差等非设计因素，各个桨叶的实际重心在空间中位置并非一致[1],组合后螺旋桨重心偏离桨轴轴线，从而使得螺旋桨在转动过程中产生较大的惯性力，使船舶在运行过程中加剧轴系同轴承间的振动和摩擦,导致轴系在加工制造过程中产生的内部微观缺陷发展成宏观裂纹，造成轴系的烧伤或断裂，影响螺旋桨使用寿命。因此，在桨叶制造完成后，需要对其重心位置进行评价和相应的重心修正处理，以满足设计指标和工作要求。

目前在桨叶重心评价方面的相关研究成果主要有:戈贲奇等[2]以螺旋桨叶片前端的不平衡质量为标准,对桨叶重心是否合格进行判定;谢伟[3]将传统的挂重法进行改进，以螺旋桨静平衡性能为标准，进行桨叶重心的评价。在实际工程中,对桨叶重心的修正主要依靠加工量估算和手工反复打磨，虽然该方法操作简单、实施灵活，但加工质量难以保证。相关学者针对重心修正问题提出了一些改进方法：于颖等[4]根据桨叶曲面加工精度和公差的要求，应用计算机辅助工艺方法，求取加工过程中最小修正质量；李芳[5]通过图像处理方法得出桨叶重心位置的偏差值,对桨叶进行打磨加工以修正重心；顾毅君等[6]以桨叶螺距误差最小为目标，利用粒子群优化算法对螺旋桨加工量进行优化计算；曾艳等[7]针对桨叶毛坯的形状误差，利用改进的遗传算法实现最优加工余量的计算。但目前尚未提出一种具有完整理论依据且计算效率高的重心误差评价和重心修正方法。

本文针对组合式螺旋桨桨叶重心误差评价问题，提出重心最小包容球和重心公差球的概念，判定是否需要对桨叶重心误差进行修正，给出分别以最小修正质量和最小桨叶重心离散程度为评价标准的修正方案，最后利用ADAMS对组合式螺旋桨优化前后主轴力学性能进行仿真对比，验证该重心评价和修正方案的有效性。

1　重心最小包容球

1.1最小闭包球概念

定义n维空间Rn是一个以c点为中心,以r(r>0)为半径的球Bcr,可以表示为

Bcr={x∈Rn,‖x-c‖≤r}

(1)

其中,x表示空间Rn中任意一点,则‖x-c‖表示空间任意点距中心的Euclidean范数即距离范数。

在Rn空间中,设定其中m个点的集合为S={P1,P2,…,Pm},那么最小闭包球定义为能够包含S中所有m个点且具有最小半径的空间球[8]。

1.2重心最小包容球表式

对于组合式螺旋桨,每个桨叶的重心可以看作桨叶重心集合中的一点。理论上组合式螺旋桨各桨叶形状完全一致，因而各个桨叶重心完全重合。实际上由于桨叶在成形加工过程中受制造精度、材料缺陷及装配误差等非设计因素的影响，组合式螺旋桨的实际重心位置与理论设计重心位置并不一致。

参考最小闭包球的概念可知，有且仅存在一个球域，半径最小并能够包含空间所有的重心点,该空间球域即为桨叶重心点的最小包容球。

如果设组合式螺旋桨由n个桨叶片组成,定义n个桨叶的重心坐标分别为C1(x1,y1,z1),C2(x2,y2,z2),…,Cn(xn,yn,zn),根据最小包容球的定义,重心最小包容球可表示为各个桨叶重心坐标的集合C={C1,C2,…,Cn}。

1.3重心最小包容球判定与桨叶最小包容球算法

在提出重心最小包容球概念后，如何确定螺旋桨桨叶的重心最小包容球仍需要详细说明,但数学上的最小闭包球算法过于复杂,适用于大规模数据点的处理[9],而组合式螺旋桨一般由3到5个桨叶组成,因此本文仅针对组合式船桨提出桨叶重心的最小包容球判定准则与算法。

最小包容球的判定需要满足以下两个准则：①点集中所有点到最小包容球球心的距离小于等于最小包容球的半径;②最小包容球边界上的点所确定的最小包容球等价于原点集的最小包容球。

由最小包容球判定准则可知，在边界点确定的情况之下，如果非边界点都在边界点所确定的最小包容球内部，则可确定点集的最小包容球即为该边界点所确定的最小包容球，按照这种思想可以求解出点集的最小包容球。因此，根据常用组合式螺旋桨的桨叶数量分别就三叶桨、四叶桨以及五叶桨三种情况进行讨论。

对于三叶桨,在桨叶空间中其重心连线为三角形，若三角形为锐角，作三角形的外接圆，以该外接圆为中截面作球，该球即为桨叶重心的最小包容球，如图1a所示；若三角形为钝角三角形或直角三角形，则以最长边为直径作球，该球即为重心最小包容球，如图1b所示。

(a)锐角三角形重心连线(b)非锐角三角形重心连线图1　三叶桨桨叶重心的最小包容球

对于四叶桨，在桨叶空间中其重心连线为四面体，作四面体的外接球。若球心在四面体的内部，则该外接球为桨叶重心的最小包容球，如图2a所示；若球心在四面体的外部，则找到距离球心最近的四面体表面，过表面三角形作外接圆，以该外接圆为中截面作球，该球即为桨叶重心的最小包容球，如图2b所示。

(a)重心在四面体内部(b)重心在四面体外部图2　四叶桨桨叶重心的最小包容球

对于五叶桨，任选三个桨叶重心作其包容球，其组合数共有10种，再任选4个桨叶重心作其包容球，组合数共有5种。取满足最小包容球判定原则①且半径最小的包容球作为五叶桨重心的最小包容球。

为了验证该算法的有效性,引入一组实际测得的四叶桨桨叶重心数据来求其重心最小包容球,如表1所示,经计算可以得到近似球心位置为C0(-47.154 mm,50.31 mm,685.27 mm),半径R=1.206 mm。

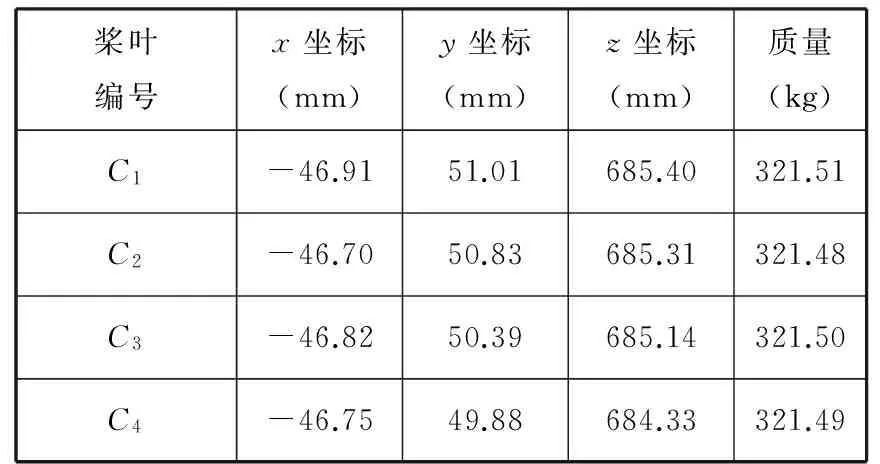
表1　桨叶重心坐标和质量

2　桨叶重心公差球

2.1重心公差球概念

由上文可知,组合式螺旋桨的各个桨叶的重心位置存在于重心最小包容球内。为了调整和优化螺旋桨的重心位置，需要对相关桨叶进行判定与修正，然而如何对桨叶重心进行评价仍需要进一步研究,因此本文提出桨叶重心公差球的概念。重心公差球是指能够包容尽可能多桨叶重心点的空间球域,其半径为在满足性能需求时的最大半径。

2.2桨叶重心评价准则

基于最小包容球和重心公差球的概念，可以将判定桨叶是否需要进行重心修正的准则描述为：当桨叶重心公差球半径大于或等于最小包容球半径时，桨叶合格，不需要对桨叶进行去重处理；当重心公差球半径小于最小包容球半径时，需要对螺旋桨桨叶进行修正,并且重心在重心公差球外的桨叶为需要重心修正的桨叶。

2.3重心公差球的确定

重心公差球的半径为满足性能需求时的最大半径。在本问题中,半径为0.1 mm。因此确定桨叶重心公差球的过程主要是确定其球心位置。具体操作步骤如下:

(1)确定基准桨叶。考虑到桨叶材料强度、水动力学性能等因素,桨叶的修正位置选择为靠近叶梢的上半部分,因此以重心位置最低的桨叶作为修正基准桨叶,即不对此桨叶进行修正处理,将其桨叶重心位置标记为Cb(xb,yb,zb)。该桨叶重心点在重心公差球的内部。

(2)确定初始球心。以Cb(xb,yb,zb)为球心,以半径r作空间球，则该球的描述方程为

(x-xb)2+(y-yb)2+(z-zb)2=r2

(2)

如图3所示,过球心Cb沿着z轴正方向与球外表面的交点作为重心公差球的初始球心,记为Cq(xq,yq,zq)。

图3　重心公差球球心算法示意图

(3)确定重心公差球。考虑修正的桨叶越少,越节省资源，因此首先以需要修正桨叶数量最少的球为重心公差球。若存在多个球表明需要修正的桨叶的数量相同，则再以需要的修正质量之和最小的球作为最优重心公差球。为方便计算，将重心公差球球心以球坐标系形式表示。同时给出点(xq,yq,zq)的球坐标表达公式:

(3)

其中,α∈[-π/2,π/2]和β∈[0,2π]为设计变量,定义其初始值为α=π/2和β=0,考虑到计算机计算成本，设定-π/20为α的增量步长,π/20为β的增量步长,参考表1的数据,利用MATLAB编程,可以求得最优重心公差球的球心坐标为Cq(-46.75 mm,49.88 mm,684.43 mm)。

计算的最小包容球和重心公差球如图4所示,C0为最小包容球球心,Cq为重心公差球球心,4个桨叶的重心坐标分别为C1、C2、C3和C4。由于重心公差球半径小于最小包容球半径,且桨叶重心C2不在重心公差球内，因此需要对C2所在的螺旋桨桨叶进行重量去除加工以修正重心。

图4　最小包容球和重心公差球

3　重心修正

3.1桨叶重心修正位置的确定

在确定需要进行重心修正的桨叶后,要确定桨叶的修正区域，要求在该区域进行重心修正后,可以使桨叶重心移动到重心公差球内，满足使用要求。由于修正之后的桨叶重心满足重心组合原理，即修正后桨叶的重心和桨叶上修正点合成的位置点为修正之前的桨叶重心。因此，由几何知识可知，过不合格桨叶重心A，作重心公差球的外切圆锥，该圆锥的反向延长与桨叶的交线所围成的区域即为桨叶的修正区域。过重心公差球之中的点B，向不合格桨叶重心方向作映射线，与桨叶表面的交点C即为对应的修正位置,如图5所示。

图5　修正位置确定示意图

3.2去除质量最小修正方案

在修正区域进行质量去除加工，可以使该桨叶重心移动到重心公差球内，满足设计要求。考虑螺旋桨水动力性能因素，桨叶在修正加工之后，表面形状相应发生改变，修正质量越大，桨叶表面形状改变越大，对水动力性能影响越大，修正质量应该尽可能小，因此提出以最小修正质量为标准，确定桨叶上最优修正位置及修正质量。

设修正点到不合格桨叶重心的距离L1,不合格桨叶重心与重心公差球上对应点的距离L2,重心修正前不合格桨叶的质量为q,修正质量为Δq,根据重心组合原理,可知:

(q-Δq)L2=ΔqL1

(4)

求解式(4)可得：

(5)

令a=L1/L2,根据式(5),可以求出在修正区域各点的修正质量,当修正质量Δq最小,即a取得最大值时,修正区域上对应的点为最优修正点。

3.3重心离散程度最小修正方案

在同一坐标系中,各桨叶的重心点离散程度越小，即可认为桨叶相似程度越高，则组装之后的螺旋桨在转动过程中的力学性能越好。因此不合格桨叶修正后的重心应该是在重心公差球内使所有桨叶重心离散程度最小的点。在数理统计中，常用描述数据离散程度的度量值有极差(全距)、平均绝对偏差和方差等，但极差容易受到数据极端值的影响，平均绝对偏差在数学处理上不方便，而方差不仅可以反映数据的离散程度又便于数学上的处理，因此选用方差评价各桨叶重心的离散程度。

设组合式螺旋桨由N个桨叶组成,当存在一个不合格桨叶时，设合格桨叶的重心坐标Ci(xi,yi,zi),i=1,2,…,N-1,不合格桨叶经过重心修正后的重心坐标为Ck(xk,yk,zk),则经过修正后的不合格桨叶的重心坐标到其他重心点坐的距离方差可表示为

(6)

式(6)是关于xk、yk、zk的二次曲线,图形开口向上。其中，所有桨叶重心坐标的平均值为

(7)

当不合格桨叶重心修正后的重心坐标等于其他合格桨叶重心坐标的平均值时,方差取最小值,此时组合式螺旋桨的桨叶重心点离散程度最小,即

(8)

由于各种非设计因素的存在,组合式螺旋桨的各个桨叶的实际重量并不完全相同，因此在计算桨叶平均重心位置时需要考虑各个桨叶的重量wi,进行加权平均值的计算,加权平均值的算法为

(9)

基于上述推导可知,当不合格桨叶经过重心修正后,重心位于合格桨叶重心的加权平均值时,方差最小,各桨叶重心离散程度最小,此时该点为最优重心点。

将表1中各桨叶重心坐标和质量代入式(9)可计算出不合格桨叶的最优重心点坐标为(-47.01 mm,50.94 mm,685.5 mm)。

4　仿真验证

4.1理论分析

在进行桨叶重心修正之前,由于不合格桨叶重心存在较大偏差,在安装之后,螺旋桨的重心不在桨轴中心线上,螺旋桨在绕桨轴中心线旋转过程中，合格桨叶产生的离心力合力大小为F1,不合格桨叶产生的离心力合力大小为F2，它们之间存在一个夹角αo,因而桨轴会产生一个偏心力,大小为FD,如图6所示,FD的表达式为

(10)

E处和F处轴承会分别给桨轴提供相应的支承力,其大小分别为FE和FF,设EF段长l1,DE段长l2,则由力学平衡可知：

(11)

图6　桨轴受剪力和弯矩图

E处所受弯矩大小为

ME=FDl2

(12)

由图6可以看出,桨轴的危险截面即在支承E处,因此对E截面进行力学分析与仿真,由式(9)可知,当不合格桨叶重心修正之后,各桨叶重心坐标更加接近,转动时产生的离心力F1与F2大小趋于相等,夹角αo趋于180°,相应偏心力FD减小,进而截面E处受到剪力和弯矩均减小,螺旋桨力学性能得到改善。

4.2力学仿真验证

在动力学分析软件ADAMS的仿真环境中,刚体在受力情况下无法产生弹性变形[10],而实际工作情况中,桨轴的形变会引起质量分布的改变,桨轴的转动和柔性桨轴的变形是相耦合的,因此,传统的刚体动力学分析无法满足要求,为了模拟实际工作情况，利用ADAMS中Flex模块实现螺旋桨的刚柔耦合仿真分析。仿真中采用转速为120r/min,额定转矩为1.95×105N·m的永磁同步电机定转速驱动,并设置仿真时间为30s,步长为3000。

螺旋桨工作过程中,桨轴自由端变形最大,因此对其D处的径向位移变化情况进行仿真分析,如图7a所示;根据理论分析可知，桨轴的危险截面在后支承E处,因此以该截面作为仿真对象,对比螺旋桨重心修正前后受到剪力和弯矩变化情况,如图7b和图7c所示。

(a)位移变化曲线

(b)剪力变化曲线

(c)弯矩变化曲线图7　重心修正前后桨轴力学性能变化曲线

由图7可知,位移曲线、受力曲线和弯矩曲线在刚启动时有较大的波动，是因为仿真中施加定转速驱动，软件在仿真开始时需要设定系统初值，随着时间的增长各曲线逐渐收敛，各曲线在稳定后仍有小幅度的波动,这是由柔性体在工作过程中的振颤引起的,与实际情况相符,仿真结果如表2所示。

由表2可知,经过两种方案进行重心修正后桨轴危险截面处受力和力矩有较大的减小， 自由端振动情况也有不同程度的改善，其中重心离散程度最小方案效果更为明显，危险截面处受剪力相对修正前减小了68.45%,所受弯矩减少了57.69%,延长了螺旋桨的使用寿命；自由端径向位移相对修正前减少了63.10%,改善了螺旋桨的动平衡性能，减少了振动和噪声。

表2　重心修正前后仿真结果

5　结论

(1)针对船桨桨叶重心误差评价问题,提出重心的最小包容球和重心公差球的概念，并给出具体算法，为桨叶重心评价提供可靠的理论依据。

(2)根据重心组合原理，给出了修正区域的确定方法，并分别以最小修正质量和最小桨叶重心离散程度为标准提出最优修正方案。

(3)对修正前后螺旋桨主轴的力学性能进行分析，仿真结果与理论分析结果相符。

(4)结果表明螺旋桨在重心评价和两种重心修正方案优化后，力学性能较修正前有不同程度的改善，有效地减小了重心偏差对螺旋桨的影响，其中修正质量最小方案修正后的桨叶表面形状改变较小，进而对螺旋桨水动力性能影响较小；以最小离散程度方案修正后的螺旋桨的力学性能改善效果更明显。所提出的重心评价和修正方法也为类似的多桨叶组合桨的重心改善问题提供可靠的参考依据。

[1]梁延德,郭超,王治雄,等.大型复杂曲面工件重心倾侧方法研究[J].组合机床与自动化加工技术,2013(12):1-3.

Liang Yande,Guo Chao,Wang Zhixiong,et al.Study on the Tilt Measurement of the Gravity Center for Large Workpiece with Complex Surface[J].Modular Machine Tool and Automatic Manufacturing Technique,2013(12):1-3.

[2]戈贲奇,朱新河.船用铜合金螺旋桨的检验要点分析[J].大连海事大学学报,2005,31(2):55-58.

Ge Benqi,Zhu Xinhe.Examination Important Point Analysis of the Marine Propeller Made of Copper Alloy[J].Journal of Dalian Maritime University,2005,31(2):55-58.

[3]谢伟.五叶调距桨的桨叶优化组合及整桨静平衡方法研究[J].舰船科学技术,2004,26(5):7-10.

Xie Wei.Study on Optimum Combination of Blades of Five-blade Controllable-pitch Propeller and Static Balancing Methods of the Whole Propeller[J].Ship Science and Technology,2004,26(5):7-10.

[4]于颖,於孝春,关琦.螺旋桨桨叶叶面加工过程中加工量的计算[J].机械设计与制造,2003(5):100-101.

Yu Ying,Yu Xiaochun,Guan Qi.Calculation of Manufacturing Value of the Curve Surface of Blades of the Propeller[J].Machinery Design and Manufacture,2003,5:100-101.

[5]李芳.桨叶重心检测系统设计[C]//中国智能交通年会优秀论文集.北京:中国智能交通协会,2009:90-92.

[6]顾毅君,徐冰强,陆金桂,等.粒子群优化算法在螺旋桨加工量计算中的应用[J].现代制造工程,2009,8(1):6-8.

Gu Yijun,Xu Bingqiang,Lu Jingui,et al.The Application of PSO Algorithm on Computing Manufacturing Allowance of Propeller[J].Modern Manufacturing Engineering,2009,8(1):6-8.

[7]曾艳,李斌,彭芳瑜,等.面向数控加工的大型螺旋桨桨叶的余量估算问题研究[J].中国机械工程,2006,17(3):566-569.

Zeng Yan,Li Bin,Peng Fangyu,et al.Research on the Estimation of the Propeller Allowance in NC Machining[J].China Mechanical Engineering,2006,17(3):566-569.

[8]Yildirim E A.Two Algorithms for the Minimum Enclosing Ball Problem[J].SIAM Journal on Optimization,2009,19(3):1368-1391.

[9]Pan Shaohua,Li Xingsi.An Efficient Algorithm for the Smallest Enclosing Ball Problem in High Dimensions[J].Applied Mathematics and Computation,2006,172(1):49-61.

[10]金鑫,何玉林,刘桦,等.风力发电机耦合振动分析[J].振动与冲击,2007,26(8):144-147.

Jin Xin,He Yulin,Liu Hua,et al.Coupled Vibration Analysis of Wind Turbine[J].Journal of Vibration and Shock,2007,26(8):144-147.

(编辑袁兴玲)

Barycenter Error Evaluation and Correction for Modular Marine Propeller

Liang YandeSun JiefuHe FubenLu Yaheng

Dalian University of Technology,Dalian,116024

In the process of blade manufacturing,there existed the influences of manufacturing precision,material defects,assembling errors and other non-design factors,which caused the difference between actual position and theoretical position of modular marine propeller barycenters.There would have adverse effects on its mechanical properties.Hence,it was necessary to evaluate the barycenters and remove the weights so as to correct the barycenter position errors of relevant blades.The concepts and the algorithms of minimum containing ball and removal processing ball were proposed,which could be applied to determine whether the blade needed to be re-processed.Meanwhile,regarding the barycenter combination,two weight correction solutions were also proposed based on the principles of the minimum amount of correction weight and the minimum dispersion degree of barycenter respectively.In the end,the feasibility of strategy was evaluated by applying theoretical analysis and simulation experiments.

modular marine propeller;minimum containing ball;removal processing ball;minimum correction weight;degree of barycenter dispersion

2014-04-02

TH161DOI：10.3969/j.issn.1004-132X.2015.06.009

梁延德,男,1953年生。大连理工大学机械工程学院教授。研究方向为先进制造技术,精密加工。孙捷夫,男,1991年生。大连理工大学机械工程学院硕士研究生。何福本,男,1984年生。大连理工大学机械工程学院博士研究生。鲁亚恒,男,1991年生。大连理工大学机械工程学院硕士研究生。