液压型风力发电机组主传动系统压力控制特性研究

艾　超　叶壮壮　孔祥东　廖利辉

1.燕山大学河北省重型机械流体动力传输与控制实验室,秦皇岛,0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,066004

液压型风力发电机组主传动系统压力控制特性研究

艾超1,2叶壮壮1,2孔祥东1,2廖利辉1,2

1.燕山大学河北省重型机械流体动力传输与控制实验室,秦皇岛,0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,066004

液压型风力发电机组主传动系统为定量泵-变量马达闭式系统，风机并网后依靠变量马达变排量机构对系统进行控制。研究了系统压力控制特性，建立了并网后主传动系统数学模型,得出了系统压力对马达斜盘摆角的传递函数。利用MATLAB辨识工具箱，根据实验数据，对系统压力控制模型进行数据辨识，并与理论模型进行对比，验证了理论模型的准确性，为液压型风力发电机组通过压力控制实现最佳功率追踪控制奠定理论与实验基础。

风力发电;定量泵-变量马达;压力控制;数据辨识

0　引言

自20世纪80年代美国等发达国家建立示范风电场以来，风能成为电网新电源[1]。风能作为可持续发展的绿色新能源,越来越受到世界各国的关注,许多国家都开始发展风电产业[2]。其中,对于液压型风力发电机组的研究，代表性机构有挪威的Chapdrive公司、德国亚琛工业大学以及苏格兰的Artemis Intelligent Power公司等[3]。

传统风机(齿轮式以及永磁同步式)主要是对发电机端的转矩进行控制(直接转矩控制法),以实现整个发电机组的并网控制[4]。液压型风力发电机组主传动系统的控制是通过改变变量马达的斜盘摆角来实现的[5],即通过改变斜盘摆角来改变系统高压压力。系统的高压压力直接关系到发电机的发电功率以及风力机的转速。压力控制环作为此种机型的基础控制环节，对其控制特性进行研究是非常重要的。

本文详细推导了系统压力关于马达摆角的传递函数表达式,分析了系统压力动态响应特性的影响因素，并利用MATLAB辨识工具箱对实验数据进行辨识，得到了30 kV·A实验系统的压力响应传递函数。

1　液压型风力发电机组工作原理

图1为液压型风力发电机组工作原理图,机组主要由风力机、定量泵-变量马达闭式液压主传动系统及励磁同步发电机组成。机组采用定量泵-变量马达闭式液压系统作为主传动系统,液压马达与励磁同步发电机刚性连接，省掉了传统风力发电机组中发电机与电网之间必须使用的变流逆变装备，而是直接并网运行，并网状态下励磁同步发电机的转速由于电网的作用而稳定于1500 r/min的同步转速，图2为液压型风力发电机组定量泵-变量马达主传动系统分析原理图[6]。

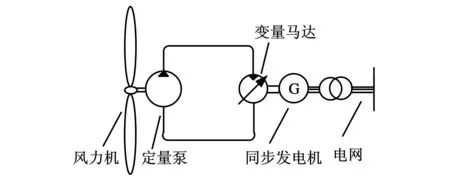
图1　液压型风力发电机组工作原理图

图2　主传动系统分析原理图

2　主传动系统压力控制数学模型与仿真分析

2.1数学模型的建立

在建立定量泵-变量马达调速回路数学模型时,做以下几点假设:①连接管道为刚性管且长度尽可能短，忽略管道中的压力损失;②系统中流体的流动状态均是层流;③每个腔室内的压力是均匀相等的，液体密度为常数;④不考虑补油系统的影响。

(1)定量泵流量方程为

qp=Dpωp-Cip(ph-pl)-Cepph

(1)

其增量方程的拉氏变换式为

Qp=Dpωp-Ctpph

(2)

式中,Dp为定量泵排量;ωp为定量泵角转速;Cip为定量泵内泄漏系数;Cep为定量泵外泄漏系数;ph为高压压力;pl为低压压力;Ctp为定量泵总泄漏系数。

(2)变量马达流量方程为

(3)

由于γ和dθm/dt都是变量,因此它们的乘积具有非线性,采用泰勒级数展开的方式进行线性化处理有

(4)

忽略二阶无穷小量后式(4)可简化为

(5)

将式(5)代入式(3),并取其增量方程的拉氏变换为

(6)

式中,Cim为液压马达的内泄漏系数；Cem为液压马达的外泄漏系数;Ctm为液压马达的总泄漏系数,Ctm=Cim+Cem;Km为变量马达排量梯度;γ为变马达变量机构摆角,在[0,1]区间取量纲一数值;γ0为变量马达变量机构初始摆角;ωm为变量马达的角速度；ωm0为变量马达的初始角速度;θm为变量马达角位移；θm0为变量马达初始角位移;V0为定量泵和变量马达之间高压管路总容积;βe为油液综合体积弹性模量。

(3)定量泵和变量马达之间高压腔的流量连续方程。联立式(2)和式(6)得

(7)

(4)系统压力关于变量马达摆角的传递函数。整理式(7)即可求出系统压力关于变量马达摆角的传递函数如下：

(8)

式中,Ct为总的泄漏系数,Ct=Ctp+Ctm。

利用式(8),结合液压主传动系统控制形式得到压力控制框图,如图3所示。其中,Jm为液压马达转动惯量，Bm为液压马达的黏性阻力。

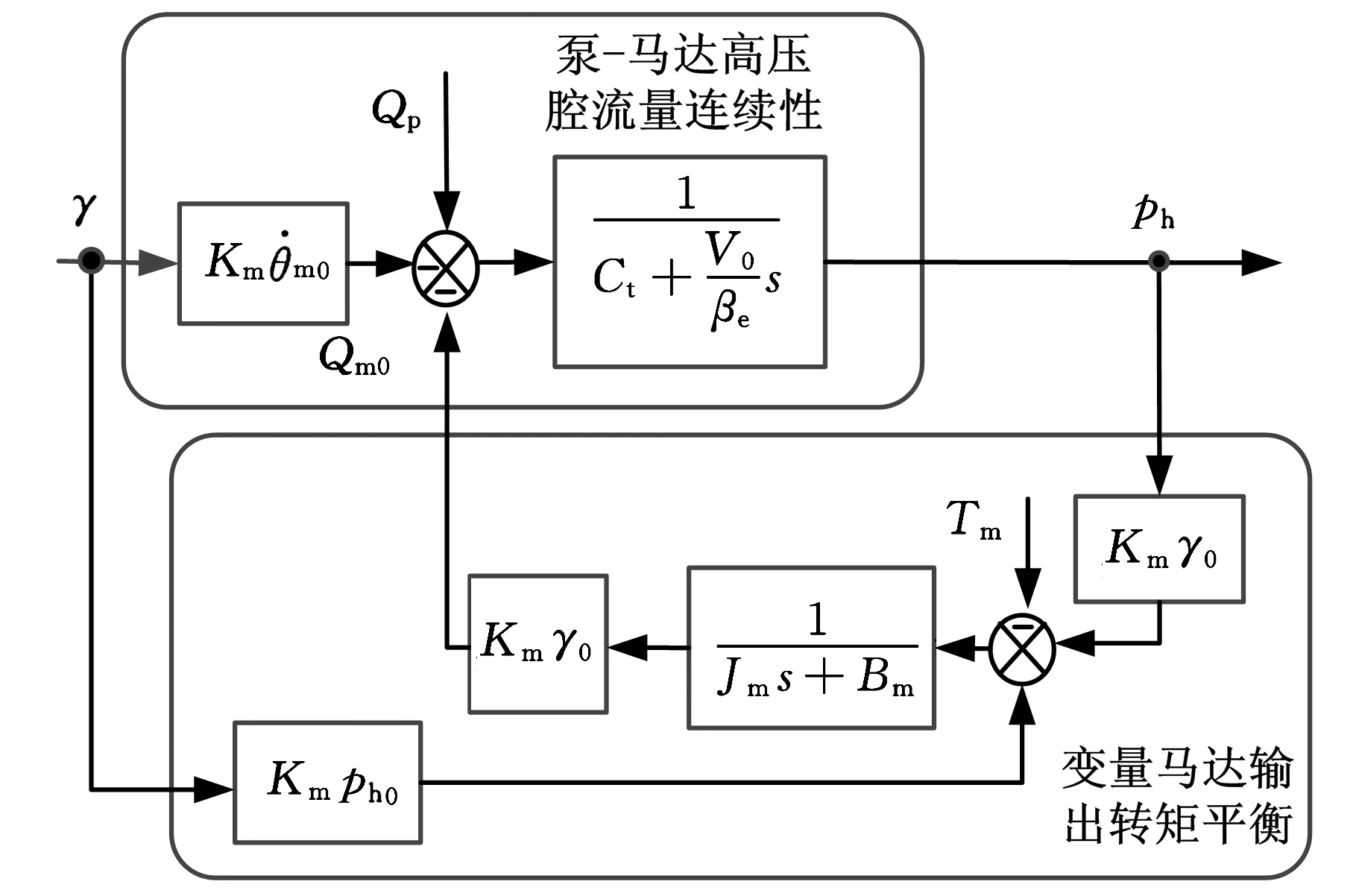
图3　液压系统压力控制框图

当发电机并入电网后，由于电网与发电机的相互作用，马达负载转矩Tm可实时跟随液压系统压力变化。不考虑容积效率,系统流量平衡时,定量泵的流量与变量马达的流量相等,由于控制框图是由增量表达式推导出来的，所以Qp=Qm0=0,则式(8)可化简为

(9)

定义压力对变量马达摆角增益Kp γ=Kmωm0/Ct。

系统压力是系统功率响应的中间变量(液压系统传输功率P=Kmωm0γph),欲提高发电功率，首先要提高系统压力。由式(9)可知,系统压力关于变量马达摆角的传递函数是一个典型的惯性环节和比例环节，并且系统压力变化量只与马达摆角变化量有关，与系统初始压力和摆角初始位置无关。

2.2传递函数阶跃响应仿真分析

由于泄漏系数与油液综合体积弹性模量在正常实验时可认为是变化不大的[7],所以搭建系统仿真模型时,我们重点分析了高压腔容积V0对系统特性的影响。

给定马达摆角一阶跃信号,高压压力变化值的阶跃响应曲线如图4所示(模型参数取值如表1所示)。

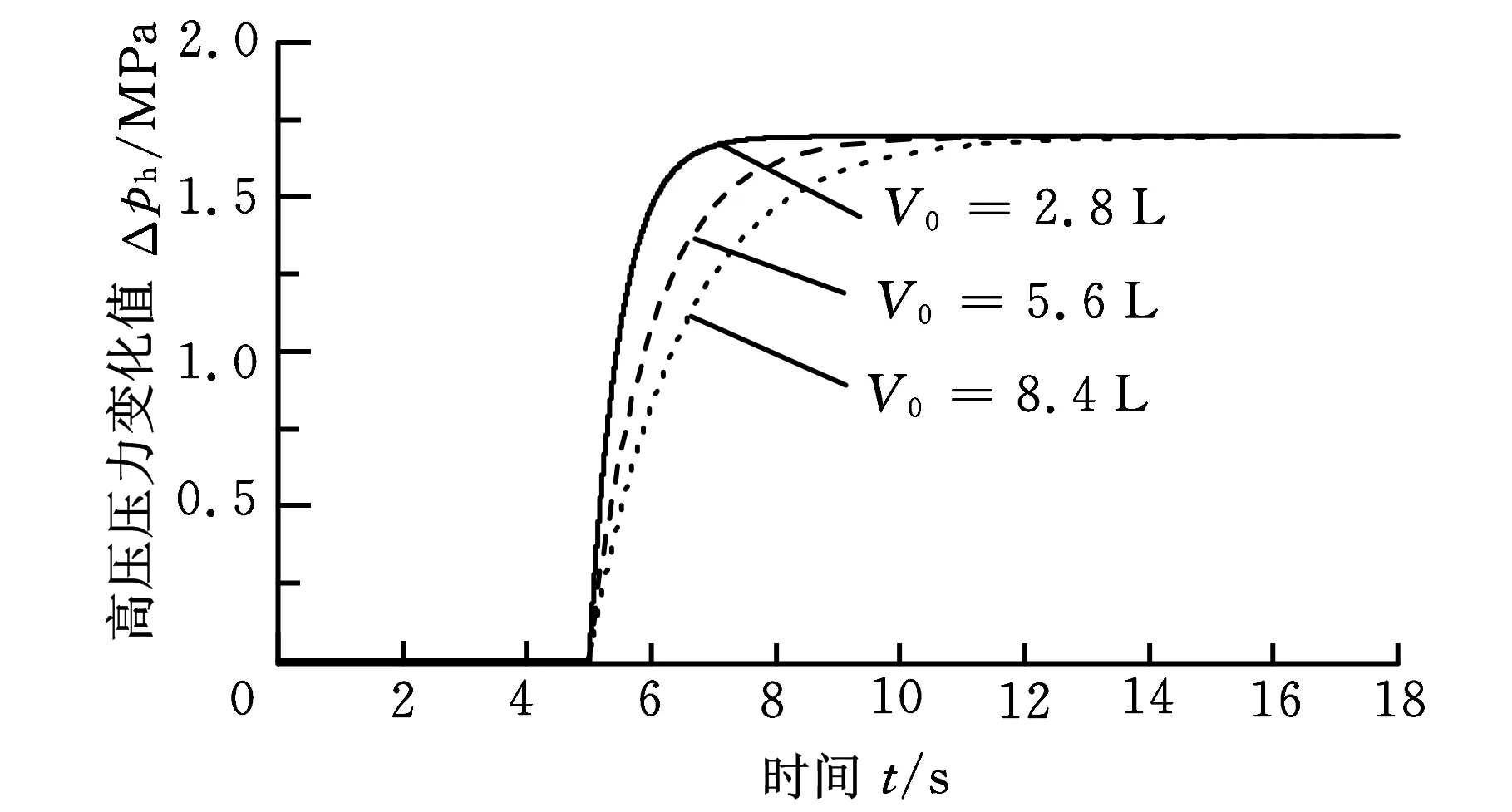
图4　不同V0值下的压力变化响应曲线

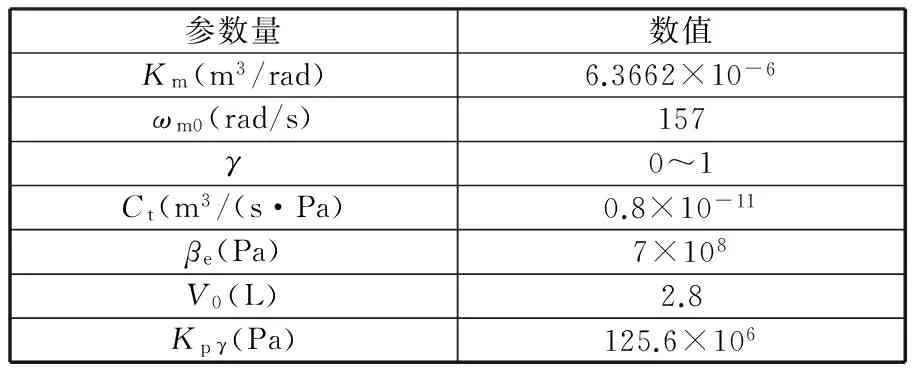
参数量数值Km(m3/rad)6.3662×10-6ωm0(rad/s)157γ0～1Ct(m3/(s·Pa)0.8×10-11βe(Pa)7×108V0(L)2.8Kpγ(Pa)125.6×106

在5 s时,给定马达摆角同一阶跃变化值,对于三个不同高压腔容积V0值,可以看出压力响应有明显的差异。响应时间随着V0的增大而增大,且受V0的影响较为显著。所以为了提高系统压力动态响应特性,希望系统的初始容积越小越好。

3　主传动系统压力关于马达摆角变化实验分析

图5为30kV·A液压型风力发电机组实验平台实物图，实验平台主要由风力机模拟系统、定量泵-变量马达液压主传动系统以及并网发电系统组成。实验系统参数值如表1所示。

图5　30 kV·A液压型风力发电机组实验平台实物图

在一定定量泵转速下，给定马达摆角阶跃变化值，系统压力和马达摆角变化曲线如图6所示(定量泵转速800 r/min,马达摆角给定0.855～0.835)。

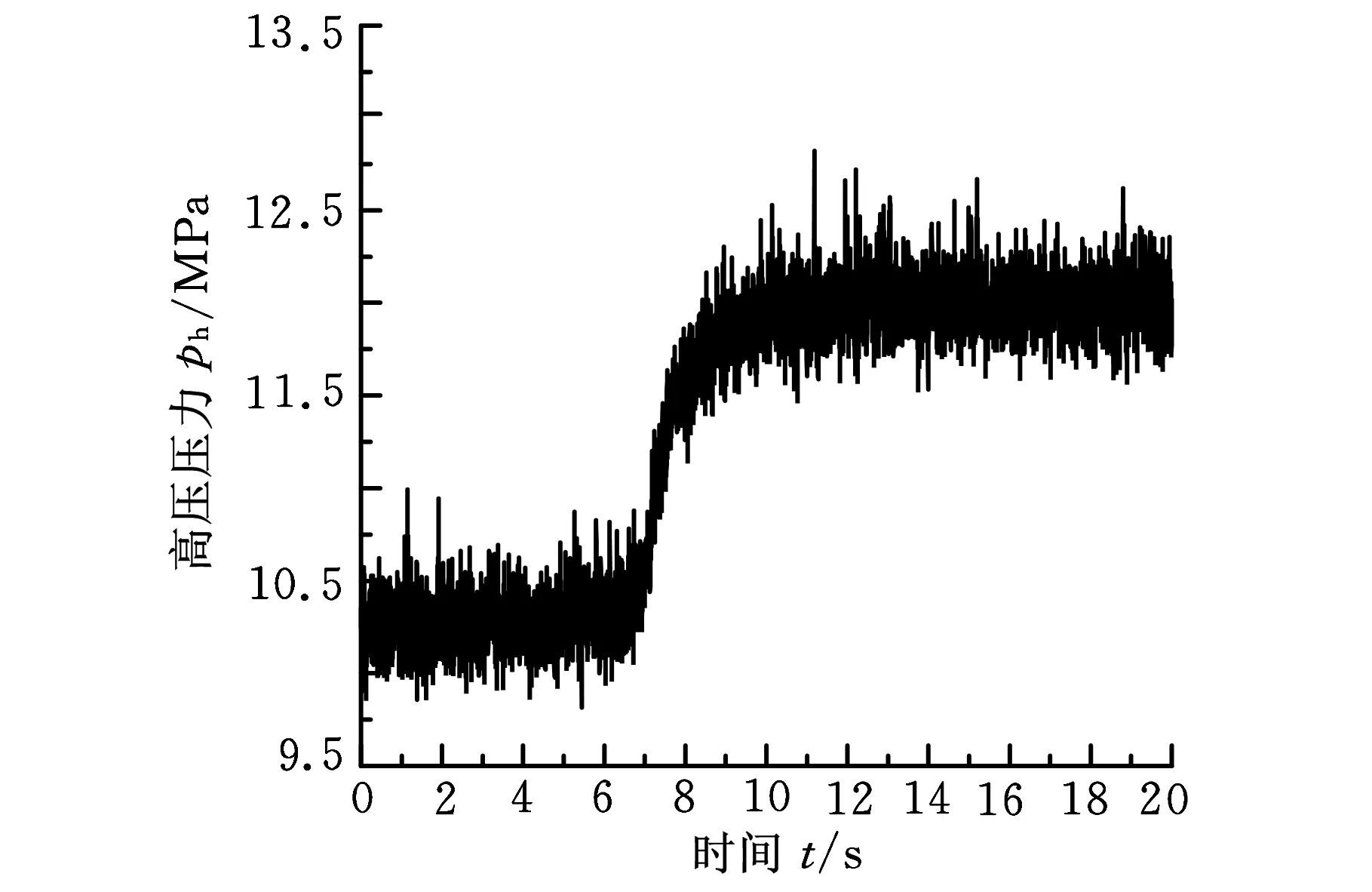
(a)压力响应曲线

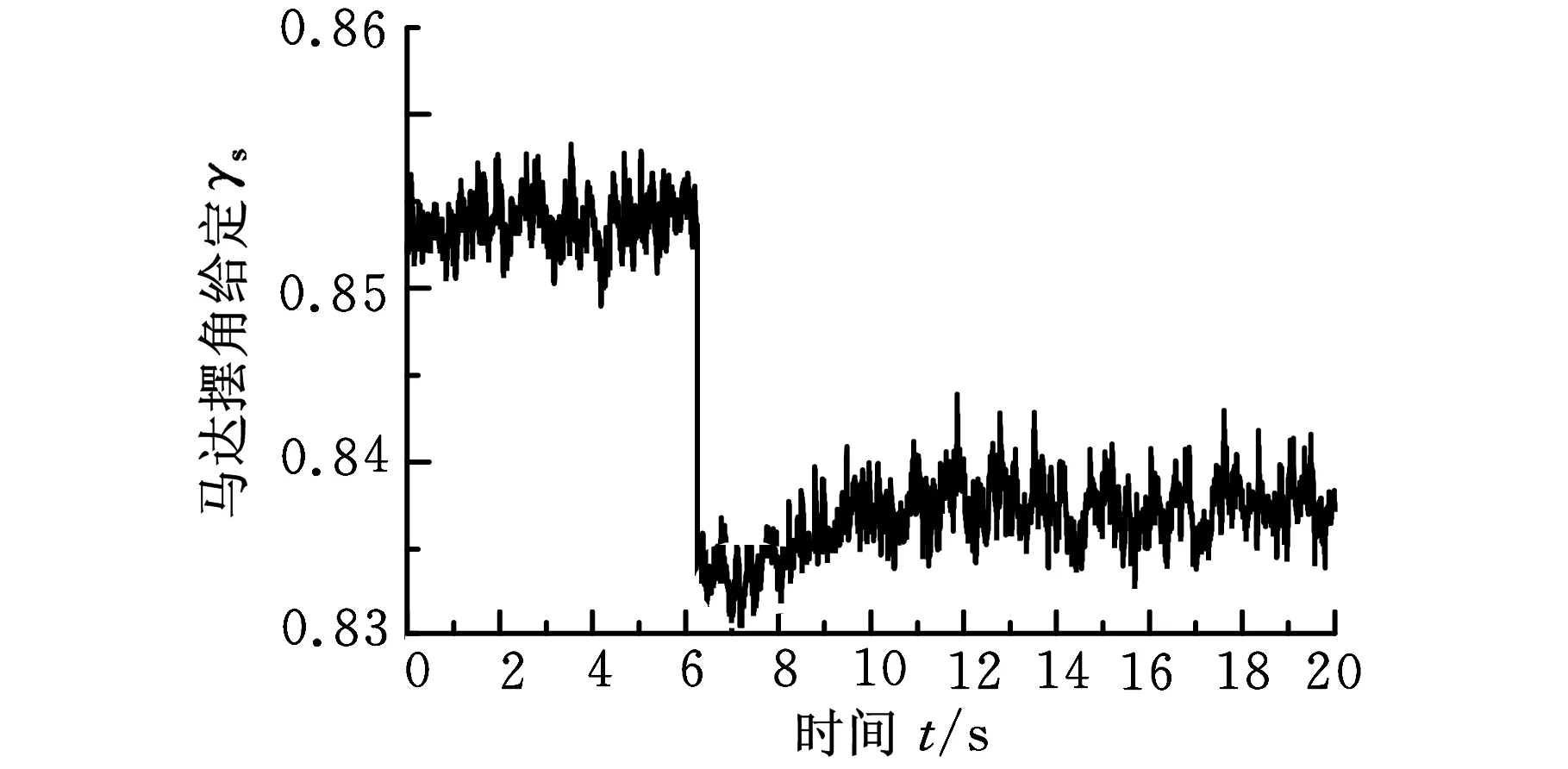
(b)摆角给定曲线图6　系统压力对马达摆角变化响应实验曲线

实际上,马达摆角(即摆角真实值)的阶跃给定由摆角补偿值确定，马达摆角真实值由斜盘基准值和斜盘偏差组成，在控制的时候调定斜盘偏差即可完成信号的给定。

从图6可以看出,压力响应曲线稍微滞后于摆角给定曲线，压力响应无超调,响应时间2 s左右。同时，可以看出压力响应曲线和理论仿真曲线(图4)趋势较为接近，这也验证了理论建模的准确性。

为了准确得到系统压力对马达摆角的传递函数，我们利用MATLAB辨识工具箱[8]对实验数据进行辨识，辨识结果如图7所示，可得系统压力对马达摆角传递函数为

(10)

系统压力所用单位为bar,1 bar=100 kPa。

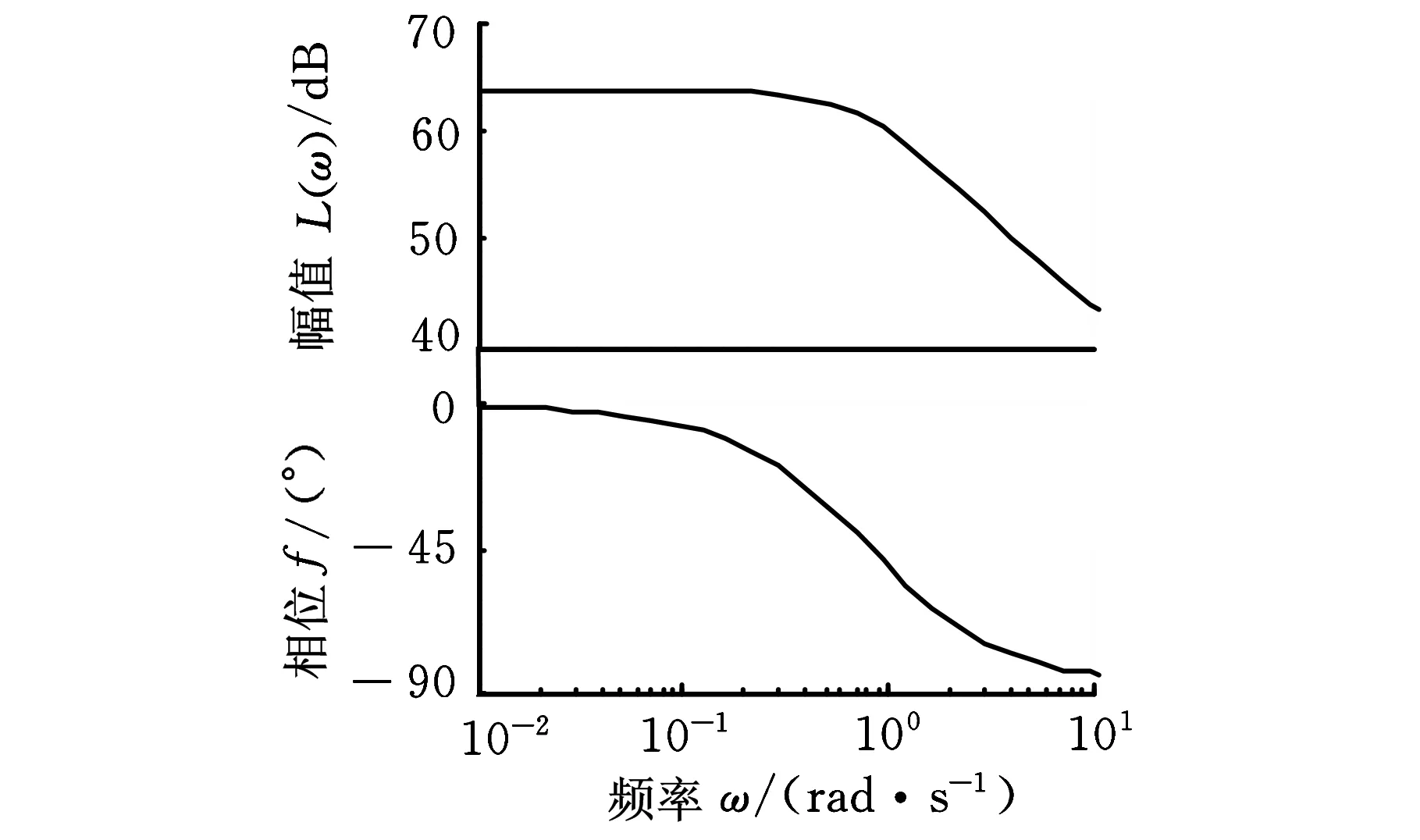
(a)伯德图

(b)辨识结果图7　系统压力对马达摆角变化的辨识结果

伯德图如图7a所示,辨识精度如图7b所示,由于惯性时间常数为V0/(βeCt),比例系数为Kmωm0/Ct,所以有

(11)

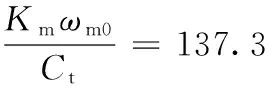
(12)

式(11)中V0与βe受系统结构、外部环境等方面因素影响不能得到精确值,而式(12)中Km是马达排量梯度、ωm0是马达角转速，其值可以明确得到。根据式(12)求出此液压系统此时的总泄漏系数Ct为0.73×10-11m3/(s·Pa)。实验数值与理论数值(表1)较为接近,但值得注意的是，经辨识方法求得的泄漏系数为系统采集该实验数据时的对应值，系统在运行过程中会发生一定的变化。

4　结论

(1)本文以液压型风力发电机组液压主传动系统为研究对象,建立了定量泵-变量马达液压主传动系统压力控制数学模型。

(2)通过所建立的数学模型，分析得出以下结论:系统压力关于马达斜盘摆角的传递函数由典型的惯性环节和比例环节组成，且与液压主传动系统的初始状态无关，而其响应特性与高压腔容积有明显的关系，响应时间随着容积的增大而变长。

(3)基于30 kV·A液压型风力发电机组实验平台，本文对压力关于马达摆角变化进行了实验分析,利用MATLAB辨识工具箱对实验数据进行系统辨识，验证了理论分析的正确性，为下一步研究泄漏系数对惯性时间常数的影响奠定了基础。

[1]刘德顺,戴巨川,胡燕平,等.现代大型风电机组现状与发展趋势[J].中国机械工程,2013,24(1):125-126.

Liu Deshun,Dai Juchuan, Hu Yanping,et al.Status and Development Trends of Modern Large-scale Wind Turbines[J]. China Mechanical Engineering, 2013,24(1):125-126.

[2]GWEC. Globle Wind Report 2013[R].Belgium: Global Wind Energy Council,2014.

[3]Diepeveen N F B.On the Application of Fluid Power Transmission in Offshore Wind Turbines[D].Netherlands:TU Delft,2013.

[4]林志明,潘东浩,王贵子,等.双馈式变速变桨风力发电机组的转矩控制[J].中国电机工程学报,2009,29(32):118-123.

Lin Zhiming,Pan Donghao,Wang Guizi,et al. Torque Control of Doubly-fed Variable Speed Variable Pitch Wind Turbine[J].Proceedings of the CSEE,2009,29(32):118-123.

[5]孔祥东,艾超,王静.液压型风力发电机组主传动控制系统综述[J].液压与气动,2013(1):1-6.

Kong Xiangdong,Ai Chao,Wang Jing.A Summary on the Control System of Hydrostatic Drive Train for Wind Turbines[J].Chinese Hydraulics & Pneumatics,2013(1):1-6.

[6]张刚.液压型风力发电机组主传动系统功率控制研究[D].秦皇岛:燕山大学,2012.

[7]薛晓虎.液压系统缝隙内流体泄漏特性的分析[J].机械工程学报,2004,40(6):75-80.

Xue Xiaohu.Analysis on the Fluid-Leakage Characteristic in Gaps of the Hydraulic System[J].Journal of Mechanical Engineering,2004,40(6):75-80.

[8]刘数军,盖晓华,樊京,等.MATLAB7.0控制系统应用与实例[M].北京:机械工业出版社,2006.

(编辑袁兴玲)

Pressure Control Characteristics of Main Transmission System of Hydraulic Transmission Wind Energy Conversion System

Ai Chao1,2Ye Zhuangzhuang1,2Kong Xiangdong1,2Liao Lihui1,2

1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science(Yanshan University),Ministry of Education of China,Qinhuangdao,Hebei,066004

Fixed displacement pump-variable displacement motor is the main drive system of hydraulic type wind turbine,the system is controlled by a variable displacement mechanism after grid-connected.To study the pressure control characteristics,a mathematical model was built and the transfer function describing the pressure to the position of the motor swash plate was derived.Compared with the identified model obtained from data identification in MATLAB system,the built model was verified,which laid theoretical and test foundation for further maximum power point tracking(MPPT) based on pressure control in hydraulic type wind turbine.

wind power;fixed displacement pump-variable displacement motor;pressure control;data identification

2014-07-28

国家自然科学基金资助项目(51405423);河北省青年基金资助项目(QN20132017)；燕山大学青年教师自主研究计划资助项目(13LGB005)

TH137;TK8DOI：10.3969/j.issn.1004-132X.2015.06.004

艾超,男,1982年生。燕山大学机械工程学院讲师。主要研究方向为液压型风力发电机组。发表论文14篇。叶壮壮,男,1990年生。燕山大学机械工程学院硕士研究生。孔祥东,男,1959年生。燕山大学机械工程学院教授、博士研究生导师。廖利辉,男,1986年生。燕山大学机械工程学院硕士研究生。