齿轮成形磨削砂轮廓形优化研究
2015-10-29丁国龙赵大兴赵东雄
丁国龙 张 颂 赵大兴 赵 迪 赵东雄
湖北工业大学,武汉,430068
齿轮成形磨削砂轮廓形优化研究
丁国龙张颂赵大兴赵迪赵东雄
湖北工业大学,武汉,430068
砂轮廓形优化对齿轮成形磨削精度和效率的影响至关重要。从齿轮端面建立了完整齿廓数学模型,其中非渐开线过渡部分采用圆弧曲线,利用无瞬心包络法求解了磨削一个齿槽的完整砂轮廓形,推导了左右固定弦齿间点解析式。调整了砂轮安装角以改变砂轮与工件的左右齿面的接触线形状和位置,使左右更对称;调整了固定弦齿间点在齿面上的位置,使之靠近分度圆,接触线分布集中,发散小。基于线性加权和法建立了多目标优化模型,以磨削效率高、左右接触线对称、单齿接触线长度最短为优化目标,利用MATLAB开发优化程序对砂轮廓形进行了优化。通过实例计算验证了调整砂轮安装角和固定点位置对砂轮廓形优化的有效性。
成形磨削;修形;砂轮廓形;接触线;优化设计
0 引言
砂轮廓形是由空间接触线在砂轮坐标系下绕砂轮轴线旋转而得到的回转曲面,不仅决定着被磨削齿轮的齿形精度,同时也影响磨齿加工效率。不同接触线可以得到不同的砂轮廓形。因此磨削过程中涉及一个重要问题——砂轮廓形的优化,即如何通过砂轮修形的定量分析与主动控制,生成满足几何条件约束和制造任务精度要求的优化的接触线,从而提高成形磨削精度和效率。
文献[1-2]中给出了成形磨齿的砂轮廓形算法,但精度较低,不能满足现实生产要求,而且没有对砂轮廓形进行分析和控制;孟石如[3]对接触线作了一定研究,认为不同砂轮半径的接触线相交于一点,称“固定弦齿间点”,但是并没有深入研究该固定点的作用与特点;郭二廓等[4]从提高磨削效率和精度出发对接触线进行了优化研究,但所建立的过渡曲线模型较繁琐,且还需要对完整的砂轮廓形进行讨论;Nishida等[5]、Yoshino等[6]对接触线进行了讨论,认为在轴向接触线长度最短时,齿形误差最小,且可改善磨削扭曲现象,但是他们也没有对砂轮廓形优化进行深入研究。在齿轮参数一定情况下,可以通过修改砂轮安装参数来调整接触线形状和位置,从而利用接触线回转来控制砂轮的廓形。
本文在上述研究的基础上,从齿轮端面建立完整齿廓数学模型。调整砂轮安装角改变砂轮与工件的左右齿面的接触线形状和位置,使左右更对称;调整固定弦齿间点在齿面上的位置,使之靠近分度圆,接触线分布集中,发散小,以期获得砂轮与齿面较优的接触特性。利用MATLAB开发优化程序对砂轮廓形进行了优化。
1 砂轮廓形方程求解
在一对共轭齿面的接触点存在公法线,当两共轭齿面之一为回转曲面时,接触点的公法线必然通过其回转轴[3]。成形砂轮磨削齿面过程中,砂轮回转面和齿面是一对共轭齿面,它们之间有满足啮合条件的瞬时接触线,该接触线绕砂轮轴线回转一周,得到的回转面即为砂轮廓形,而围绕齿轮轴线以一定的螺旋角做螺旋运动,得到的螺旋面即齿面,齿面和过渡曲面组成一个完整的齿廓。
1.1渐开线齿面及其接触线方程
无论是直齿还是斜齿,端面廓形均为渐开线形状。图1是成形磨斜齿空间接触示意图,建立工件坐标系Oxyz,以齿轮轴向为z轴,齿轮齿槽方向为x轴,x轴均分齿槽,y轴为垂直于x、z的方向;砂轮坐标系O1XYZ以砂轮轴心线为Z轴,与工件坐标系z轴夹角为Σ(安装角),X轴与工件坐标系的x轴重合,方向相反,两坐标系原点距离O O1为中心距a。

图1 成形磨斜齿坐标系示意图
图2是斜齿轮端面截形示意图。A点为渐开线上展开角为u的点M的一个曲率半径端点,M′点是M绕螺旋方向旋转θ时所得曲面上点,B为其在基圆上的曲率半径端点,δ0是渐开线基圆齿槽半角。
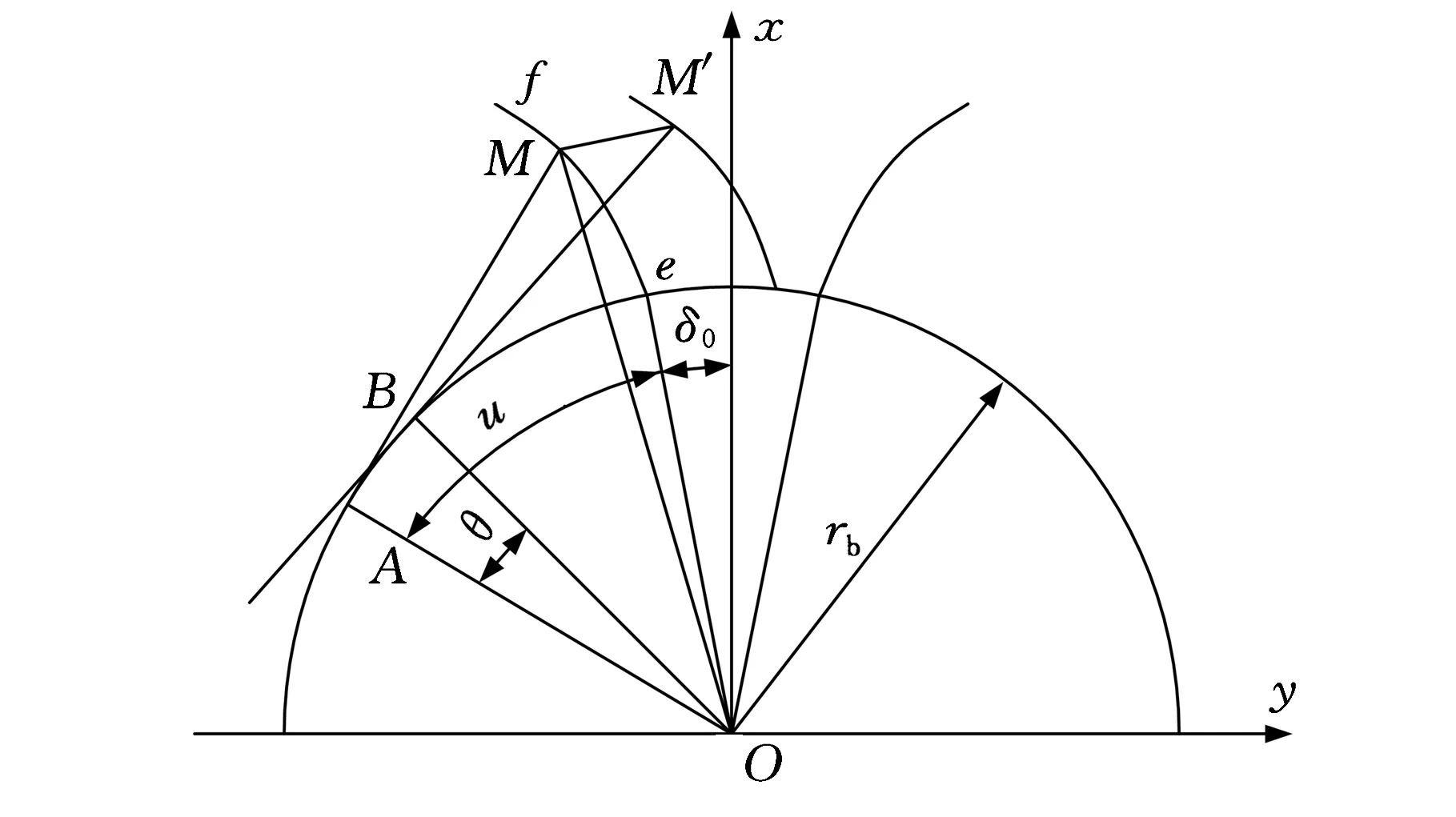
图2 斜齿端面截形示意图
对图2中取展开角u为参变量,从左齿面建立端面渐开线方程如下:
(1)
式中,rb为基圆半径。
将渐开线ef绕z轴沿螺旋角做右螺旋运动,形成齿面螺旋面,得到斜齿轮右旋左侧螺旋面方程为
(2)
其中,p=pz(2π),pz为齿轮螺旋导程,用同样方法可建立右侧齿面模型。
根据齿轮空间啮合理论知,砂轮回转面与齿轮螺旋面间的瞬时接触线必须满足一定的条件,即从砂轮坐标系原点O1向螺旋面上的点作径矢R,如果R和螺旋面上点的法线n(或在各轴上分法线nx、ny、nz)以及砂轮轴线共面,这一点就是在螺旋面上的接触点。通过计算,该接触条件整理为[7]
znx+anycotΣ+(a-x+pcotΣ)nz=0
(3)
式(3)为参变量u和θ的一个关系式,联立式(2)、式(3)和右齿面方程可求得螺旋面与砂轮在渐开线部分接触线的方程。
1.2过渡曲面及其接触线方程
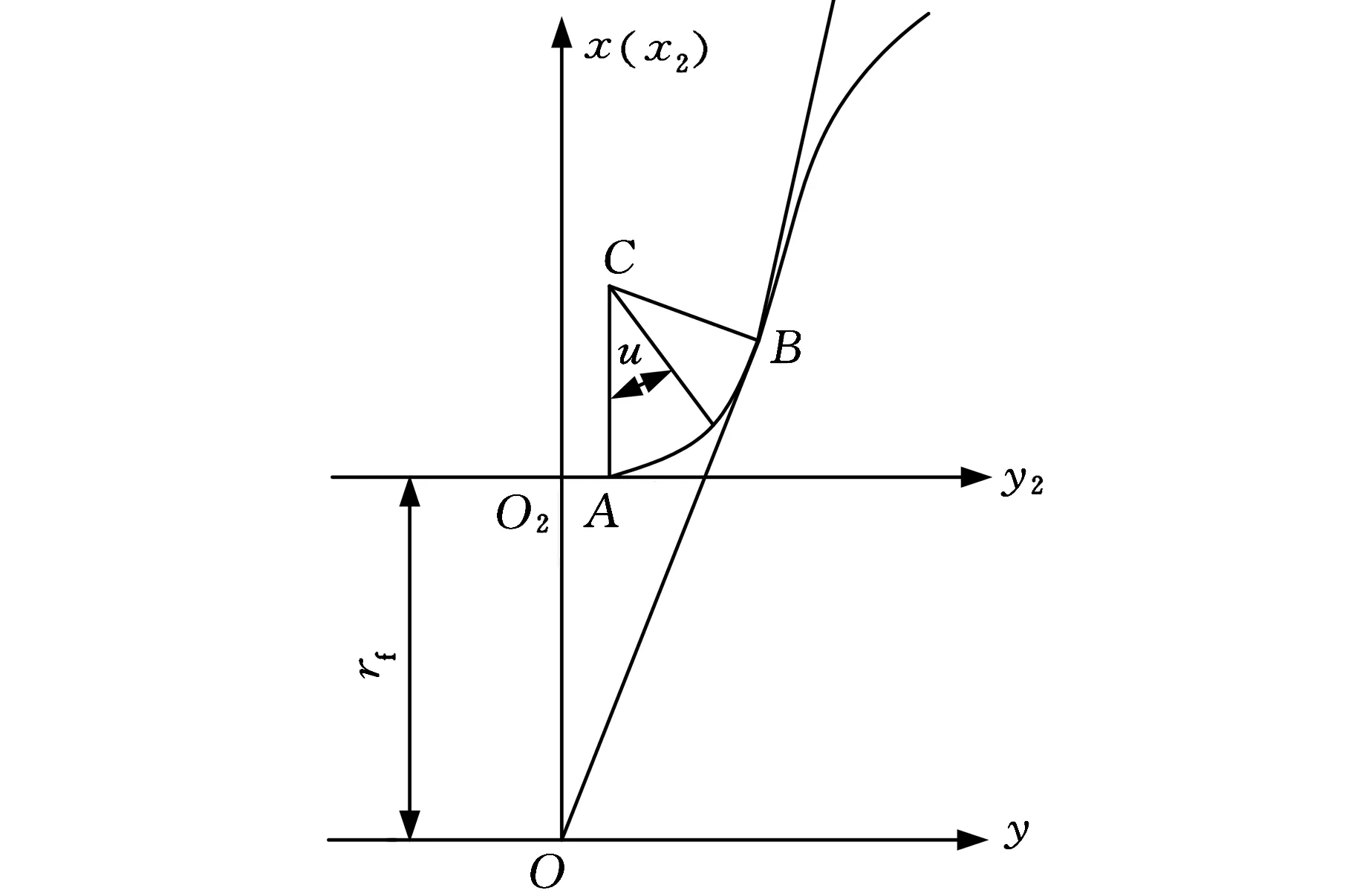
图3 齿根过渡曲线示意图
一般齿根过渡可改善应力集中的现象[8],本文采用含直线、圆弧的齿轮过渡曲线,从端面处建立过渡曲面方程。图3是齿轮齿根过渡圆弧示意图,设圆弧中心C在齿轮局部坐标系Oxy1z下的坐标为(xC,yC,0),rf为齿根圆半径,u表示圆弧段上任意一点与x轴的夹角,r为半径,取u为参变量,可建立在齿轮坐标系Oxyz的圆弧段方程为
(4)
直线段方程为
(5)
因此可得圆弧段螺旋面方程为
(6)
计算其法向量n在x、y、z轴的分量nx、ny、nz,并将其代入式(3)得圆弧接触条件式:
zpcos(u-θ)-apsin(u-θ)cotΣ+
(a-x+pcotΣ)[(xC+rf)sinu+yCcosu]=0
(7)
式(6)、式(7)联立求解可得砂轮与齿根圆弧过渡部分的接触线方程式。
1.3砂轮廓形方程
给定齿轮参数,利用数值模拟[9]、牛顿法迭代求解式(3),把满足条件式的参数u、θ代入齿廓方程式即可得到整个齿廓的接触线。而由工件坐标系Oxyz转换为砂轮坐标系O1XYZ的转换方程为
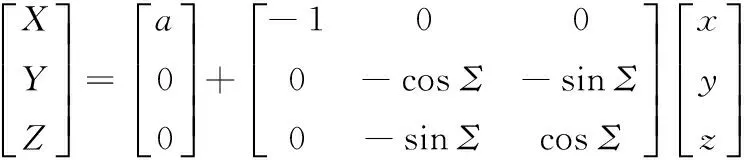
(8)
故可通过坐标转换方程式(8)把接触线转换到砂轮坐标系,所求的接触线在砂轮坐标系O1XYZ中绕砂轮轴心线Z回转,得到砂轮廓形。空间接触线转换到砂轮坐标系下的形状与位置如图4所示。为方便砂轮修形和计算,用砂轮的轴向截形(图5)来表示:
(9)

图4 砂轮上接触线示意图图5 砂轮廓形示意图
2 砂轮廓形性质及分析
在磨齿过程中,砂轮安装参数a和Σ的选择如不合适,则不仅将导致较大齿形等误差,还会使磨削效率达不到相应要求。因此分析砂轮廓形和接触线的形态随砂轮安装参数变化的规律就显得尤为重要[10-12]。
2.1接触线与安装参数关系分析
(1)砂轮与齿轮接触线不仅是空间曲线(图4),还随砂轮安装角度的变化而变化(图6)。在防止产生干涉范围内,Σ越大,单齿面上的接触线z轴高度越小,形态越直;Σ越小,渐开线部分的接触线z轴高度越大,形态也越弯曲;双齿面切削线z轴总高度随Σ增大而逐渐减小,当Σ为90°-β(β为螺旋角)附近的某一值时最小,当Σ再增大时接触线沿z轴高度随Σ增大而增大。

图6 接触线与砂轮安装角度关系
(2)对于某一参数齿轮,安装角度和砂轮半径RW不同,接触线不同(图7),但对于某一安装角而言这些接触线会相交于一个固定的点(图7中P、P1、P2点),变位系数为0时,可求出该固定点u和θ的数学表达式为
(10)

图7 固定弦齿间点与安装角、砂轮半径关系
图7中P、P1和P2为调整安装角和砂轮半径所得的固定弦齿间点,其中P点为其在分度圆上的点,线L为固定弦齿间点在yz平面的运动路径,从图中和表达式可总结出该点具有如下性质:
(1)对不同参数齿轮,该点在齿轮坐标系中位置与安装角、齿轮齿数、螺旋角以及法面压力角有关,而与砂轮半径没有关系。
(2)在Σ=90°-β时,该点位置在分度圆附近,对不同齿轮,随齿数、压力角增大,该点沿接触线向齿顶方向移动,反之则沿接触线向齿根移动。
(3)齿轮参数确定时,该固定点位置仅与砂轮安装角有关,改变安装角大小,固定点位置沿线L在齿根与齿顶间变化,其中当固定点在分度圆上时接触线分布最集中,发散最小,这时砂轮的半径变化对磨削误差影响最小,同时可避免磨削过程中在砂轮半径变化时需要调整安装角的局限,而当固定点越靠近齿顶和齿根,砂轮半径对接触线的影响越大。
(4)安装角确定时无论砂轮半径如何变化,该固定点总是为砂轮和齿轮的接触点,因而可作为齿轮磨削时的设计基准点,同时这对接触线和砂轮廓形的求解具有很大意义,可以在很大程度上提高搜索解的效率,对认识砂轮廓形也具重要理论意义。
2.2砂轮廓形与砂轮安装角关系分析
工件参数确定时,不同的砂轮安装参数有不同空间接触线,从而有不同的砂轮廓形。因此可以通过改变安装参数来改变和优化接触线、砂轮廓形等的参数,以实现高效、高精的成形磨齿加工目标。图8是确定砂轮半径RW情况下,变化安装角度Σ的砂轮廓形轴向截图。由式(10)求得接触线的固定点,利用坐标系转换方程式(8)可求得变砂轮半径情况下的砂轮廓形的固定点,该固定点可作为砂轮修形的基准点。由于砂轮廓形随砂轮与齿轮的相对安装位置(砂轮安装角度Σ)不同而各异,因此在采用不同的砂轮安装角度时,砂轮修形所需去除的材料量不一样,形状不同,修整效率、精度不同,故合理选择砂轮安装角非常重要。

图8 砂轮轴向截形示意图
综上所述,砂轮廓形形态受接触线的影响,而接触线形状又被砂轮安装参数(砂轮半径Rw和安装角度Σ)影响,因此工件参数确定后,造成砂轮廓形形态变化重要的参数是Rw和Σ,但由图6与图7对比知安装角度的影响占主导地位。
3 优化目标函数及求解方法
3.1变量设计及目标函数
砂轮安装角Σ对砂轮廓形的影响占主要的作用,故本文设计优化变量为Σ。在成形磨削过程中,一般Σ不等于90°-β时,对磨削过程反而是有利的。磨削时往往要求磨削时间短(效率高);沿接触线上的磨削力小而对称;单齿面接触线z轴高度小等。现分别针对不同情况建立目标评价函数。
(1)不同砂轮安装角度有不同接触线、砂轮廓形。接触线越长,同等条件下进入磨削与离开磨削阶段的时间越长,效率越低,重要的是双面同时磨削时很可能出现磨削力不对称的现象,反之,接触线越短,磨削冲程量越小,效率越高,磨削时间越短,这时的安装角度Σ对于提高效率来说是最佳安装角,由此得到的砂轮廓形为最佳廓形。鉴于此,建立效率评价函数的数学模型为
f1(Σ)=|zaL-zaR|-|zf L-zf R|
(11)
其中,zaL-zaR为左右齿面接触线在齿顶沿z轴方向的长度偏移量,zf L-zf R为左右齿面接触线在齿根沿z轴方向长度偏移量,利用数值法把齿顶和齿根相应的展开角u代入到两齿面的接触条件式(3)可分别求得其解析式,代入各参数,函数转变为关于Σ的一维数学模型,函数绝对值最小时为单目标最优。
(2)成形磨齿双面同时磨削时,左右两面磨削力存在不平衡现象,特别是在磨削首末阶段,可能出现两侧磨削力差异较大,为减小磨削振动和提高磨削精度,需要保持两侧磨削力平衡。本文以左右齿面接触线在节圆上的偏移来评价磨削力的平衡,它反映的是磨削扭转力,偏移越大,不平衡力越大。较小的偏移可以使磨削过程磨削力保持平衡,减小磨削颤振,提高效率和精度。评价数学模型表示为
f2(Σ)=pθL-pθR
(12)
其中,θL、θR分别为左齿面和右齿面的接触线在节圆上的点旋转过的角度,将确定的节圆展开角代入到各自的接触条件式即可求得,它们是关于Σ的一个一维自变量评价函数,函数最小值点的Σ为最优砂轮安装角度。
(3)单齿磨削时,接触线高度用偏置量(单齿面齿顶齿根高度偏移量)表示,该值越小,砂轮冲程量越小,磨削效率越高,同时可以提高导程修整效率。偏置量最小表示在单齿面上切削线高度最优,建立其数学评价模型如下:
f3(Σ)=zf-za
(13)
其中,zf表示齿根接触点在z轴方向坐标分量;za表示齿顶接触点在z轴方向坐标分量。把齿根与齿顶的展开角代入到齿面接触条件式(3),即可求得θ,再代入到齿面方程,可得f3(Σ)是一个关于Σ的一维方程式。
3.2优化方法
基于线性加权和方法构造评价函数如下:
f(Σ)=w1|f1(Σ)|+w2|f2(Σ)|+w3|f3(Σ)|
w1+w2+w3=1
其中,w1为双面磨削时磨削效率权系数,w2为磨削力是否平衡权系数,w3为单齿面磨削时磨削效率权系数。由于各子目标函数单位已统一,无需作量纲一处理。如以提高双面磨削效率为优化目的,则取磨削效率权系数w1=1;如以磨削过程中,磨削力对称、平衡为优化目的,则取力对称权系数w2=1;如提高单面磨削或导程修整效率为优化目的,则取单齿效率权系数w3=1。若是多目标优化,则根据重要程度选择合适的权系数。
工件参数确定后,将多目标优化转化为单目标优化,利用数值模拟思想,采用牛顿迭代方法迭代求解接触条件后代入齿廓方程,由评价函数循环搜索在特定展开角的沿z轴接触线长度,直到达到目标函数最优。
3.3优化流程
根据前面建立的各目标函数,整个优化步骤可以表示如下:
(1)建立齿廓(左齿面和右齿面、过渡曲线等)模型,并求相应的法向量和接触条件式,利用数值方法,求出砂轮与齿轮的空间接触线,利用接触线反求砂轮廓形。
(2)利用齿面、接触线方程建立砂轮廓形优化评价函数。利用线性加权和法建立多目标优化模型,并根据实际情况给出相应的权系数。
(3)利用迭代求解砂轮磨削不发生干涉的砂轮安装角度取值范围。
(4)在满足步骤(3)所求的条件下,给定Σ初值,利用数值模拟法,迭代求解f(Σ);以步长h更新Σ,再求解,直至寻求到最优的评价函数值、接触线、Σ等参数。
(5)利用式(8),将最优的接触线转换到砂轮坐标系,再将其转化到砂轮XZ或YZ平面内,从而获得砂轮轴向截形数据并输出至文件,可供后期砂轮修形等用。具体优化过程流程图见图9。

图9 优化算法流程图
4 实例及分析

图10 砂轮安装角优化系统
把以上内容内嵌到相关程序中,利用人机交互界面GUI实现输入参数并绘制各种图形、输出数据等,编写出成形磨齿砂轮安装角度优化软件,以砂轮安装角度为设计变量对砂轮廓形进行优化。图10是利用MATLAB编写的砂轮廓形优化软件主GUI及实例操作过程等,其结果是优化出砂轮廓形和安装角,该图数据为以提高磨削效率为目的对砂轮廓形进行优化的相关输出数据,其中选用基本参数如表1所示。图11为评价函数的数值示意图,其中负号只表示方向,不表示大小。

表1 齿轮磨削基本参数
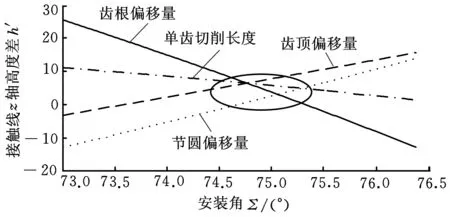
图11 评价函数值与安装角关系示意图
(1)用于评价双齿磨削效率的接触线z轴高度差如图11所示。磨削效率依靠齿根与齿顶在接触线上偏移量联合进行评价,故要求在某一安装角度时,两曲线的差值绝对值尽量小,该值越小,效率越高,磨削时间越短。由图11知,在安装角Σ=74.76°时,两曲线有交点,效率最高,此时接触线长度L=6.49 mm;而理论Σ=75°时,L=7.75 mm,使用优化后的砂轮廓形和安装角磨削,单行程每次磨削冲程量减小1.26 mm,磨削效率提高16.9%。单齿面磨削效率的评价函数值如单齿切削长度曲线,此时在防止干涉安装角范围内,取较大的安装角较为合适。
(2)磨削力对称的评价函数值如图11中节圆偏移曲线。节圆偏移量随着安装角度的增大先减小,达最小后又增大,在其值为0时最优,对应的砂轮廓形和安装角度均为最佳。通过计算得最优Σ=74.68°,接触线长度L=7.42 mm,节圆偏移为0,与理论L=7.70 mm相比,节圆偏差为2.53 mm,平衡度提高4%,用此安装角和其对应的砂轮廓形磨削加工时,磨削不平衡力最小,对称性最佳,减小磨削过程颤振,有利于提高磨齿精度。
在实际磨削过程中,应根据企业实际需求选择优化类型,以获得最佳砂轮廓形和安装角度。图11中椭圆内为进行多目标优化的优选区域,最佳接触线长度值偏向哪条曲线,由用户设定的权重因子来决定。
5 结论
(1)调整砂轮安装角和固定弦齿间点的位置,可以改变砂轮母面与齿面的接触线的形状与位置,获得优化的砂轮廓形。
(2)基于线性加权和法对砂轮廓形和接触线进行优化,通过仿真程序可以得出最佳砂轮安装角度和砂轮廓形,较传统求砂轮廓形和使用固定安装角度磨削方法更优。
(3)设计的成形磨齿砂轮廓形优化系统可运用于磨齿机系统二次开发中,在实际生产中为操作者提供最优砂轮偏转角度和砂轮廓形。同时本文利用反求及优化刀具廓形的思想可以运用到其他加工方式中,为寻求最佳刀具形状提供一种思路。
[1]夏政,黄筱调,袁鸿.一种斜齿轮成形磨砂轮截形精确求解算法[J].机械科学与技术,2012,31(8):1311-1314.
Xia Zheng,Huang Xiaodiao,Yuan Hong.A Kind of Exactitude Algorithm for Wheel Profile of the Helical-gear Form Grinding[J].Mechanical Science and Technology for Aerospace Engineering,2012,31(8)1311-1314.
[2]Kobayashi Y,Nishida N,Ougiya Y.A Profile Calculation Method for Form Grinding Wheels[J].Journal of the Japan Society for Precision Engineering,1992,58(11):1867-1872.
[3]孟石如.高精度大模数大螺旋角渐开线螺旋齿轮的成形磨削[J].机械传动,1983(1):43-52.
Meng Shiru.Form Grinding High-accuracy,Large Modulus and Big Helix Angle for Helical Gears[J].Mechanical Transmission,1983(1):43-52.
[4]郭二廓,黄筱调,袁鸿.基于提高成形磨削效率和精度的接触线优化[J].计算机集成制造系统,2013,19(1):67-74.
Guo Erkuo,Huang Xiaodiao,Yuan Hong.Contact Line Optimization for Improving Efficiency and Precision of Form Grinding[J].Computer Integrated Manufacturing Systems,2013,19(1):67-74.
[5]Nishida N,Kobayashi Y,Ougiya Y,et al.Tooth Flank Modification Processing of Helical Gears by Form Grinding Method[J].The Japan Society of Mechanical Engineers,1999,65(639):4458-4463.
[6]Yoshino H,Ikeno K.Tooth-trace Crowning in Form Grinding of Helical Gears[J].The Japan of Society of Mechenical Engineers,1991,57(538):2144-2184.[7]吴序堂.齿轮啮合原理[M].北京:机械工业出版社,2009.[8]Chiang C J,Fong Z H.Undercutting and Interferrence for Thread Form Grinding with a Tilt Angle[J].Mechanism and Machine Theory, 2009, 44: 2066-2078.
[9]Ishibashi A,Yoshino H.Design and Manufucture of Gear Cutting Tools and Gears with an Arbitrary Profile[J].The Japan Society of Mechanical Engineers,1987,30(265):1159-1166.
[10]Yoshino H.Design and Manufacture of Pinion Cutters for Finishing Gears with an Arbitrary Profile[J].The Japan Society of Mechanical Engineers,1992,35(2):313-319.
[11]宋爱平,易红,汤文成,等.渐开线弧齿圆柱齿轮及其啮合特性[J].中国机械工程,2006,17(18):1888-1891.
Song Aiping,Yi Hong,Tang Wencheng,et al.Involute Arc Cylindrical Gear and Its Mesh Characteristics[J].China Mechanical Engineering,2006,17(18):1888-1891.
[12]苏建新,邓效忠,任小中,等.基于数值模拟的内斜齿轮成形磨削砂轮修形方法[J].航空动力学报,2011,26(10):2389-2393.
Su Jianxin,Deng Xiaozhong,Ren Xiaozhong,et al.Grinding Wheel Dressing Method for Inner Helical Gear Form Grinding Based on Numerical Simulation[J].Journal of Aerospace Power,2011,26(10):2389-2393.
(编辑袁兴玲)
Optimization of Grinding Wheel Profile for Gear Form Grinding
Ding GuolongZhang SongZhao DaxingZhao DiZhao Dongxiong
Hubei University of Technology,Wuhan,430068
It is crucial that optimization of grinding wheel profile for the accuracy and efficiency of gear form grinding.A integrated mathematical model of tooth profile was established,which adopted circular curve as transition part of non-involute form of gear end-face,meanwhile,grinding wheel profile of a cogging was solved by non-instantaneous sectional envelope machining principle and analytic expression of constant intersectional point on chord tooth was derived.Adjusting grinding wheel setting angle to alter shape and position of contact line between grinding wheel and gear to make it more symmetrical;changing the position of fixed intersectional point on tooth surface to make sure it was close to pitch circle,thus the contact line was more centralized and low divergence.On the basis of using linear weighted sum method to establish muti-goal optimization module,taking highly grinding efficiency,symmetrical contact line,shortest contact line length of single tooth surface as optimization goal,the grinding wheel profile was optimized depend on programme developed on MATLAB.Finally,the effectiveness of adjusting grinding wheel setting angle and fixed point position was manifested through example’s analyses.
form grinding;dressing;wheel profile;contact line;optimization design
2013-08-20
湖北省自然科学基金资助项目(2012FFB00609);湖北工业大学博士启动基金资助项目(BSQD12008)
TG61DOI:10.3969/j.issn.1004-132X.2015.06.007
丁国龙,男,1968年生。湖北工业大学机械工程学院副教授、博士。主要研究方向为数控加工技术、机械设计等。张颂,男,1987年生。湖北工业大学机械工程学院硕士研究生。赵大兴,男,1962年生。湖北工业大学机械工程学院教授、博士。赵迪(通信作者),男,1981年生。湖北工业大学机械工程学院讲师、博士。赵东雄,男,1981年生。湖北工业大学机械工程学院硕士研究生。
