振动挖掘系统流量控制参数分析

韩　军　肖　伟　冯继新　徐　亮　顾　俊

总装工程兵科研一所,无锡,214035

振动挖掘系统流量控制参数分析

韩军肖伟冯继新徐亮顾俊

总装工程兵科研一所,无锡,214035

振动挖掘系统流量控制参数决定了振动挖掘力的特性，对振动挖掘作业效能具有重要的影响。建立了振动挖掘多连杆机构的运动学模型，推导了铲斗油缸伸长量与振动挖掘振幅的灵敏度计算公式,给出了振动挖掘力和铲斗油缸压力的求解方法，在流量控制信号输入模型中，应用傅里叶级数解决了方波、三角波振动控制信号求导问题，用数值分析方法对流量振动控制中的波形、灵敏度系数和油缸压力分布进行了分析,最后通过试验对流量振动控制模型进行了验证。

振动挖掘;运动学;挖掘力;波形;灵敏度

0　引言

振动挖掘是通过液压驱动挖掘装置的机构产生高速往复运动，使挖掘铲斗在常规静力挖掘力上叠加振动冲击力，作用于挖掘土壤的一种挖掘方式，这样可减小挖掘切削阻力,提高作业效率[1-2]。在液压挖掘机振动挖掘作业控制试验研究中，流量振动控制是振动挖掘机构动力学研究的一个重要方面。

目前,关于液压挖掘机工作装置的振动挖掘的运动学和动力学方面的研究还较少,振动挖掘方面的研究主要集中振动切削机理方面[3-7],文献[3]研究了铲斗与岩土相互作用的力学模型,探讨了液压挖掘机振动掘削的减阻规律,从而获得了振动掘削减小阻力的原因。文献[4]研究了振动载荷对土壤破碎过程的影响。文献[5]提出了基于最小二乘支持向量机(LS-SVM)的液压挖掘机振动掘削过程土壤参数在线辨识算法,进行了土壤固有频率等参数的在线辨识仿真和试验研究。Saqib等[6]研究了在甜薯收获机上利用振动挖掘铲的作业方法，研究了振动频率、幅值和前进速度对土块大小、密度和破碎方面的影响。Niyamapa等[7]研究了振动耕作工具与土壤的破碎机理之间的关系,试验表明由于振动作用,土壤出现脆性破坏时具有月牙形状的破坏面,随着振动速度增加土块大小尺寸减小。

本文建立了振动挖掘多连杆机构理论模型，给出了流量控制信号模型，对某型液压挖掘机利用数值计算方法，对其振动控制的波形、灵敏度系数和振动液压油缸的压力分布进行分析，最后利用试验对理论模型进行验证。

1　振动挖掘机构理论模型

1.1运动学模型

振动挖掘作业是通过驱动三角形机构P5P6P9,再驱动四连杆机构P6P7P9O3,使铲斗产生振动,进行振动挖掘作业的,如图1所示。

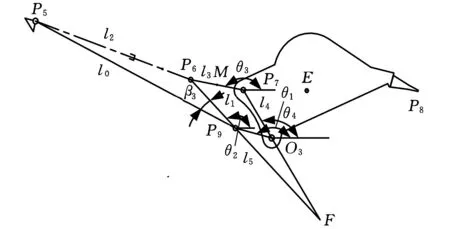
图1　铲斗四连杆机构运动模型

首先分析P5P6P9驱动机构关系。设作用于铲斗液压油缸P5P6大腔液压油分静力分力流量和振动挖掘分力流量分别为qS(t)、qV(t),液压油作用于铲斗油缸,在某一时间t,铲斗油缸的位移P5P6表示为

l2(t)=l20+l2x(t)+Δl2(t)

(1)

式中,l20为油缸未伸缩时的长度,即|P5P6|;l2x(t)为手动控制时油缸的伸长量,l2x(t)=qS(t)/S0,S0为铲斗油缸的大腔截面积;Δl2(t)为油缸输入液压振动信号时的位移量,Δl2(t)=qV(t)/S0,qV(t)可以是三角波、正弦或方波函数。

对式(1)求t的一阶和二阶导数，有

(2)

(3)

式中的一阶、二阶导数分别表示液压油缸手动控制与自动控制振动时的速度、加速度值。

对于图1中三角形机构,有

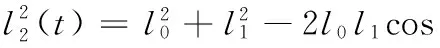
(4)

其次,利用矢量法建立双摇杆四连杆机构P6P7P9O3的运动学方程。有

(5)

对式(5)两边分别求t的一阶和二阶导数,并已知P9O3为连接架,ω1=0,ε1=0,容易得到ω3、ω4、ε3和ε4。

1.2灵敏度分析

为了得到铲斗油缸的变化量与铲斗斗齿P8点振幅的变化量关系,现在对其灵敏度进行分析。首先,对于铲斗的四连杆机构,对于某一姿态,θ1为一个定值,式(5)两边对θ2求导,得

(6)

其次,式(4)两边对β3求导数,且有dβ3=dθ2,再由dP8=lO3P8dθ4,可得

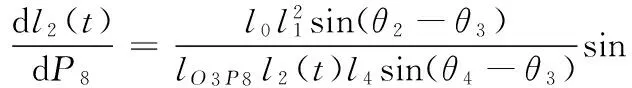
(7)

式(7)为铲斗油缸的伸长量对铲斗的偏转角度的灵敏度关系式。可知,灵敏度系数只与铲斗连杆机构的位置参数、几何参数有关。

1.3求解振动挖掘力和铲斗油缸压力模型

为了得到挖掘斗齿点的振动挖掘力,首先利用动能原理求解铲斗相对于其铰点的等效转动惯量。现在通过作图法,求连杆P6P7的运动瞬心F及其角速度ωF。容易得到:

(8)

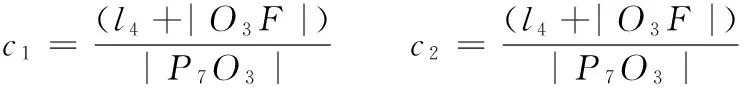
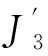
(9)

式中,m22为活塞杆的质量。

根据平衡轴定理,对于连杆P6P7,有

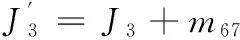
(10)

以上，P9F、P7O3、O3F和FM长度的计算均为几何运算,其计算方法较简单,这里不再详述。将式(10)代入式(9)即可得到铲斗上系统的等效转动惯量。

利用动量矩平衡原理，有

MC=JVε4

(11)

再根据FD=MC|O3P8|,即可得到作用于斗齿上的挖掘力。

令转换到铲斗油缸活塞杆上的等效质量为mV,则有

(12)

对于铲斗油缸的活塞杆m22部分,利用牛顿定理可得到铲斗油缸大腔的压力p，即

(13)

2　流量控制信号输入模型

设铲斗振动挖掘时,其振动挖掘流量qV(t)与手动控制流量qS(t)之比为λ,即

(14)

当振动挖掘输入正弦控制信号时,铲斗油缸的位移信号为

(15)

式中,qVmax为铲斗振动时产生的最大流量;f为液压流量的振动频率,Hz。

当振动挖掘输入方波控制信号时，铲斗油缸的位移信号为

(16)

式中,T为振动周期。

由于方波信号的一阶、二阶导数非连续，利用傅里叶级数将其展开，得到

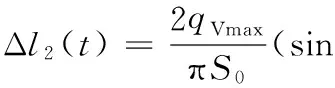
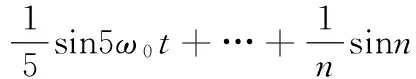
(17)

n=1,3,5,…ω0=2π/T=2πf

式(17)两边对时间t求一阶和二阶导数，容易得到输入信号的速度、加速度信号。同理，可获得三角波振动控制信号的位移、速度和加速度。

3　数值计算分析

以某型挖掘机为例,已知l0=1511 mm,l1=420 mm,l3=365 mm,l4=345 mm,l5=255 mm,铲斗质量m1=15 kg,m3=15 kg,m22=55 kg,m4=213 kg。|O3P8|=1040.6 mm,|O3E|=370 mm,铲斗摆动范围为[0°,152°]。

(1)输入不同振动控制波形，分析挖掘力分布情况。分别输入为正弦、方波和三角波振动控制信号，振动频率为10 Hz,λ=0.2,可得到铲斗斗齿点的振动挖掘力分别如图2、图3和图4所示。可以看出，正弦波输入振动控制信号产生的最大振动挖掘力约为1.9 kN,三角波信号产生的最大振动挖掘力约为26 kN,方波产生的最大振动挖掘力约为58 kN,这是由于方波信号可以产生较大的加速度值,可获得较大的振动挖掘力，而正弦信号过渡较为平缓，加速度值较小，得到的振动挖掘力值也较小，三角波振动效果位于两者之间。

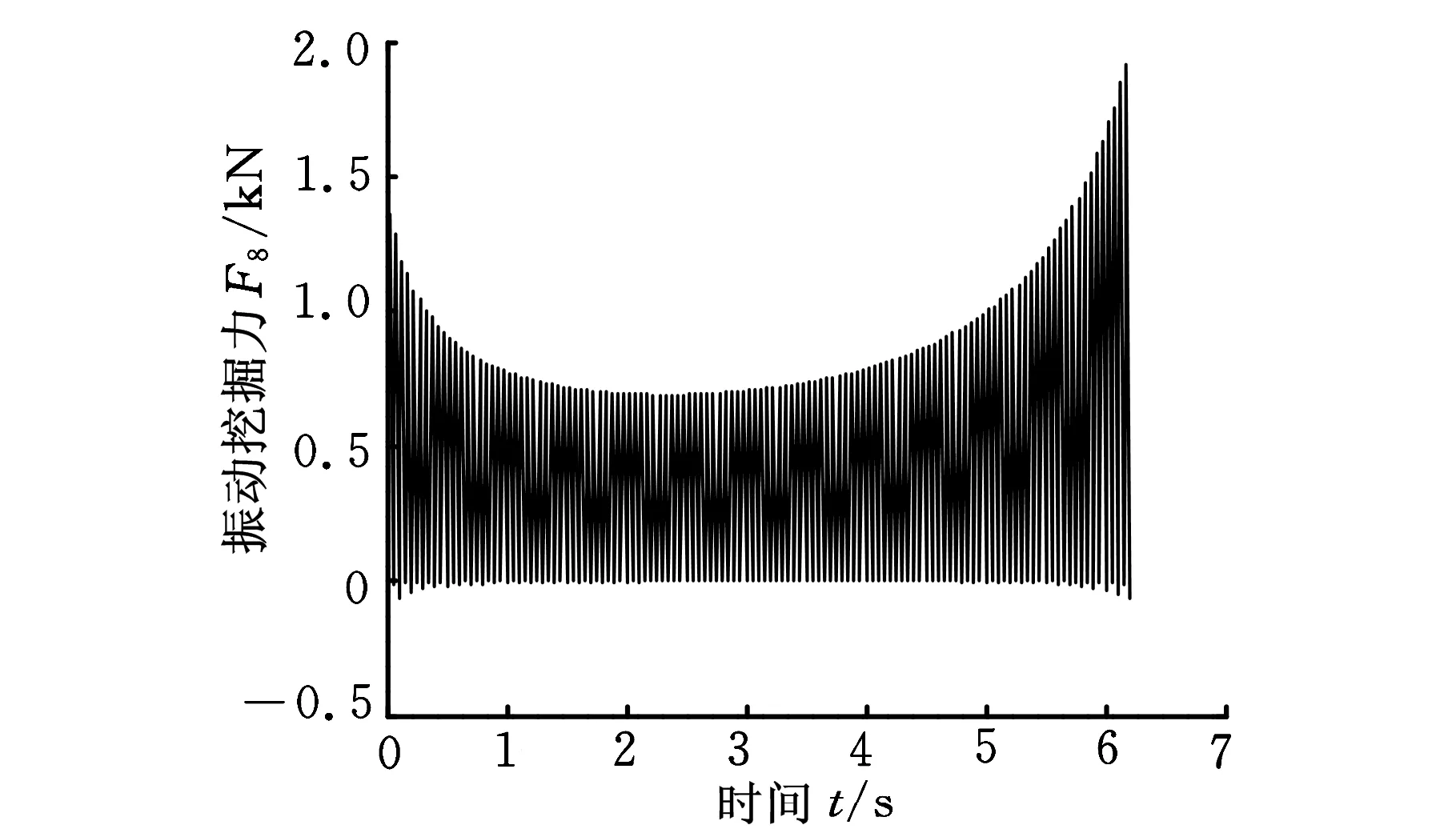
图2　正弦输入信号斗齿振动挖掘力

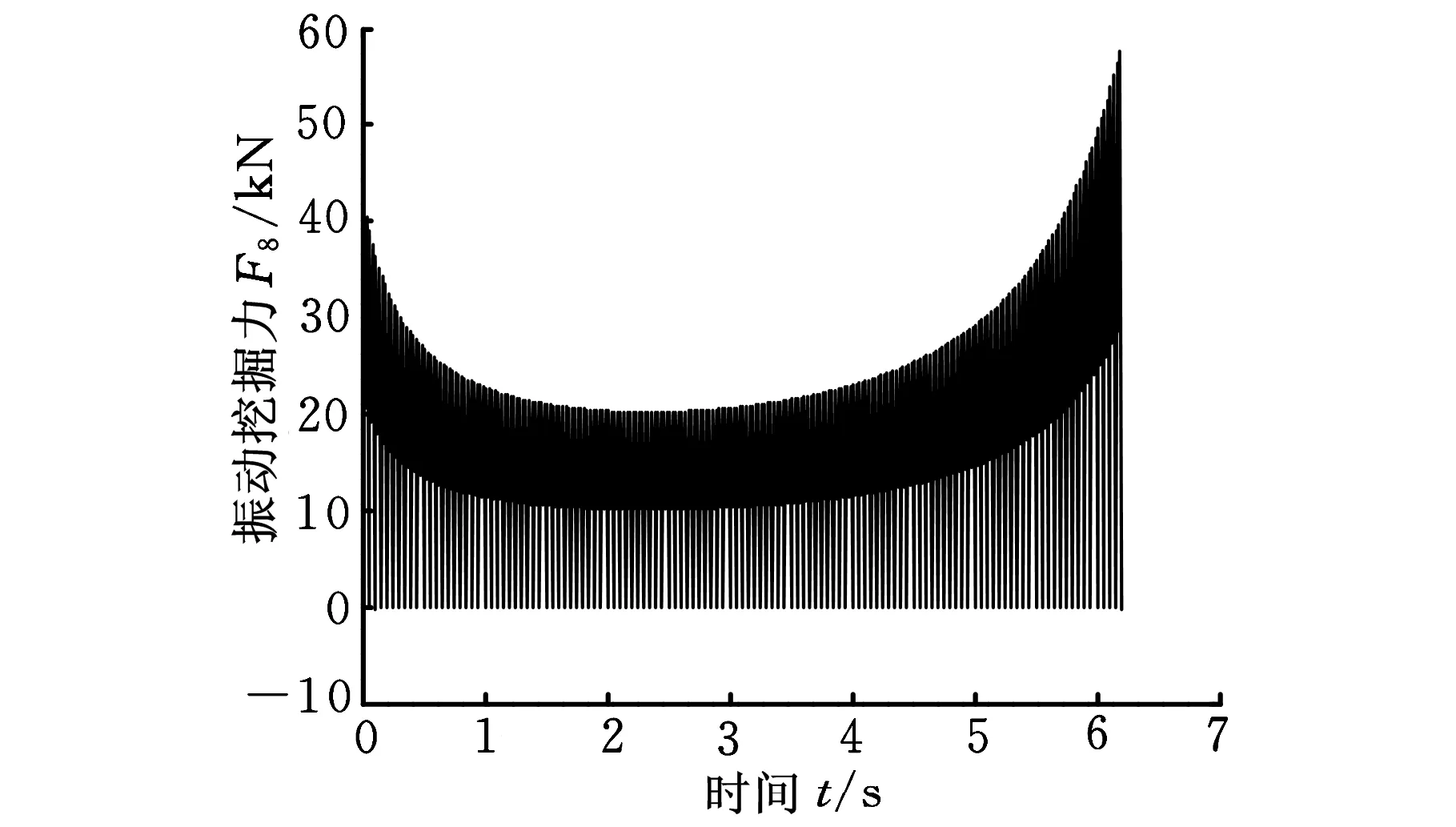
图3　方波输入信号斗齿振动挖掘力

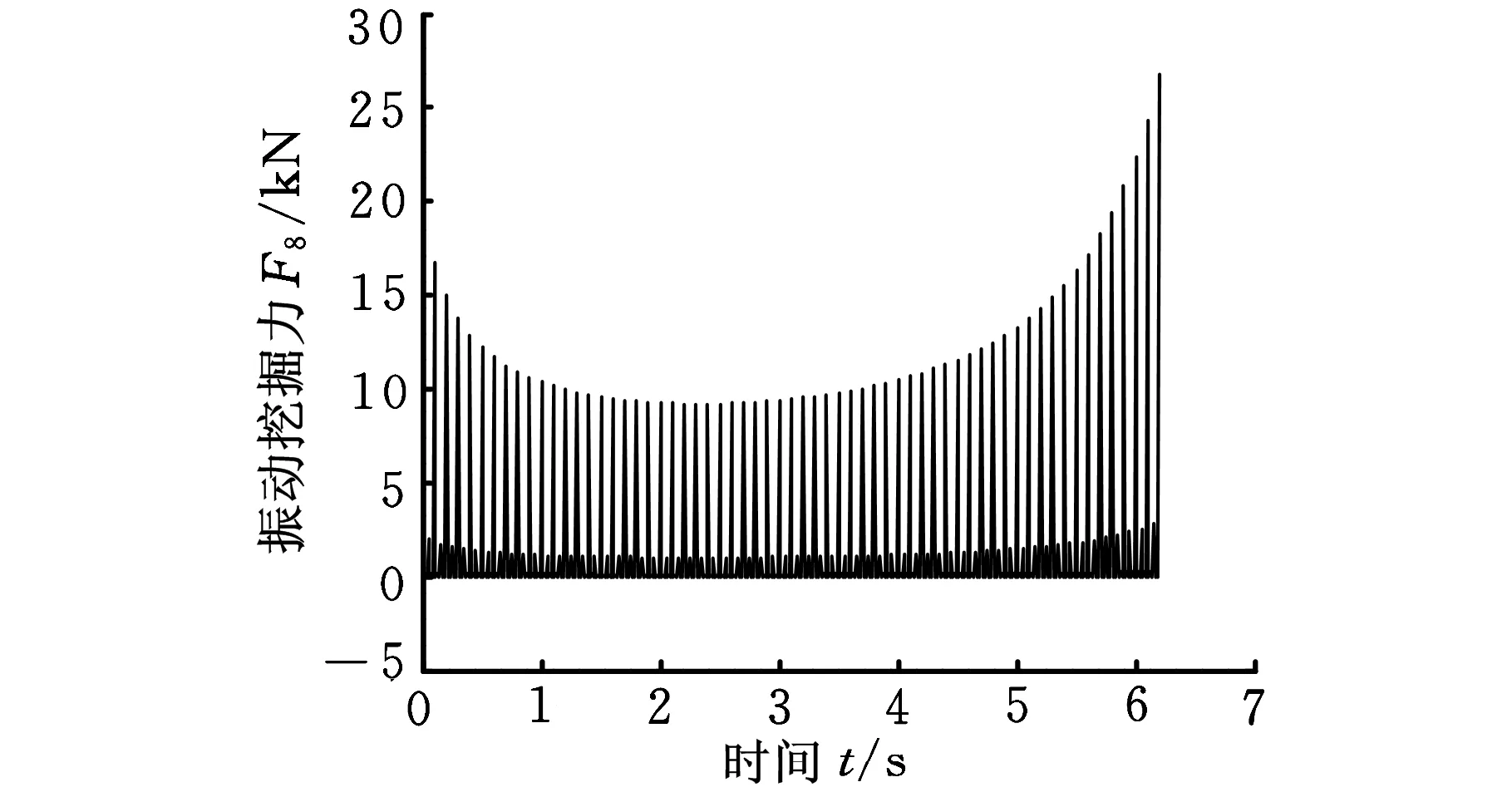
图4　三角波输入信号斗齿振动挖掘力

(2)求解铲斗油缸伸长量对斗齿点P8的振幅灵敏度系数。图5所示为铲斗驱动油缸位移关于斗齿点振幅的灵敏度系数,可以看出，铲斗驱动油缸位移关于斗齿点振动幅值的灵敏度系数随着铲斗的旋转而发生变化，最小值出现在铲斗油缸的初始位置,为0.16(最为敏感)，即铲斗油缸有1 mm位移，铲斗斗齿的振幅达到1/0.16=6.25 mm，此时，铲斗油缸的驱动力臂最短，因此，其灵敏度最高。而当铲斗油缸驱动到中间位置时，其灵敏度系数反而较大,因为此时铲斗油缸驱动的四连杆机构的力臂值较小。因此,根据灵敏度系数关系可以确定铲斗油缸的振动控制的流量，进而确定振动时的幅值。

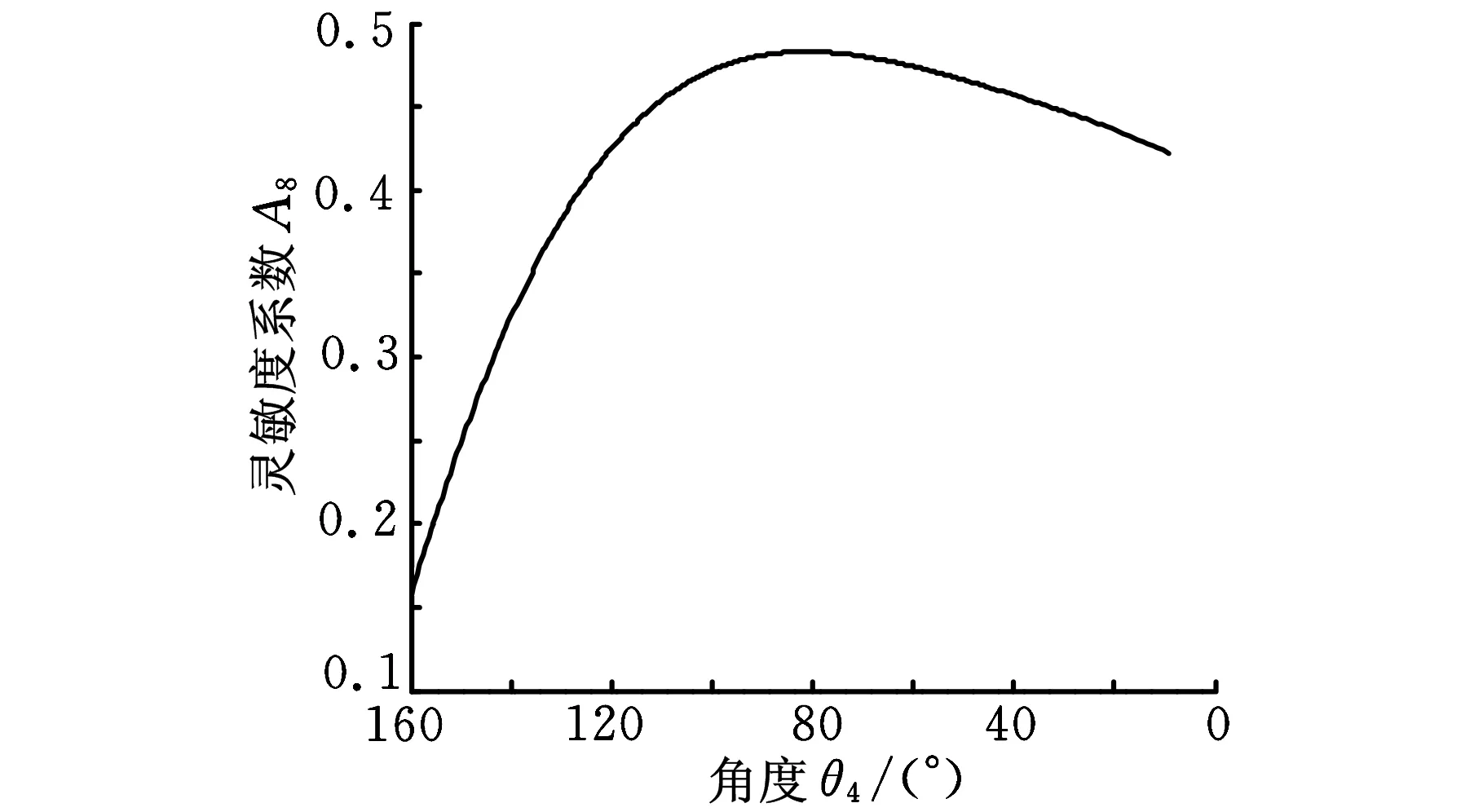
图5　活塞杆位移关于斗齿点振幅的灵敏度系数

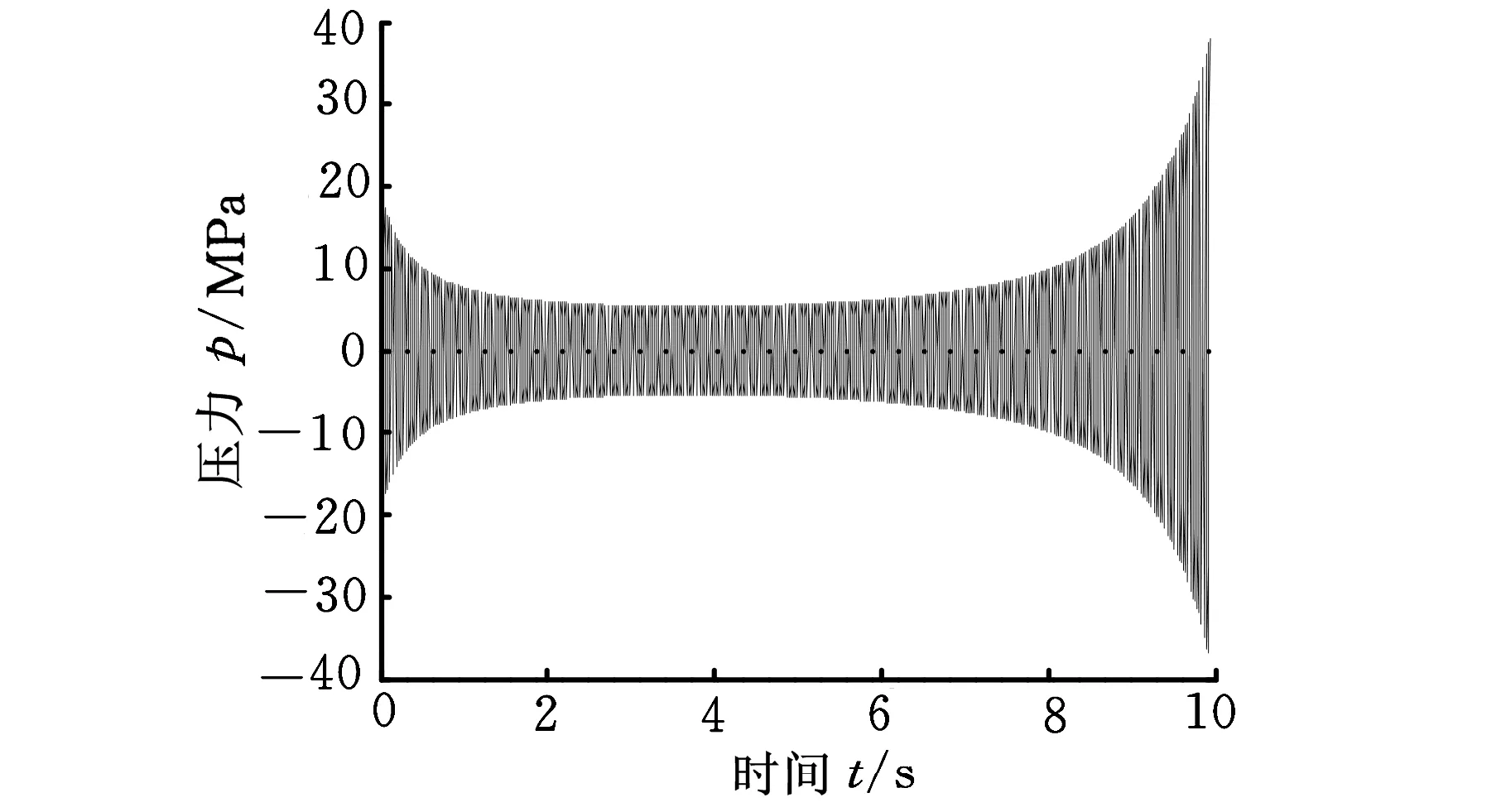
图6　铲斗油缸大腔压力变化

(3)铲斗油缸压力分布情况。图6所示为输入方波信号,振动频率为25 Hz,振动流量控制比例为0.5时,铲斗大腔的压力分布情况。从图6可以看出,该条件下铲斗大腔最大压力达到了38 MPa,超出了系统的额定压力(一般情况下为30 MPa),因此,振动控制参数的选择需要进行铲斗油缸压力理论计算，并根据液压系统的工作压力以及控制阀背压参数，对控制参数进行优化选择。

4　试验验证

为了验证流量振动控制的动力学模型，对液压挖掘机样机进行空载振动试验，测试铲斗振动油缸的压力和流量参数。在铲斗油缸上输入方波信号，驱动频率f=1/12 Hz。压力和流量测试曲线如图7所示。从测试数据看,铲斗油缸的流量近似为方波信号，振动最大流量约为56L/min,静力挖掘流量为零。铲斗油缸的最大压力为1.7MPa(17bar)。

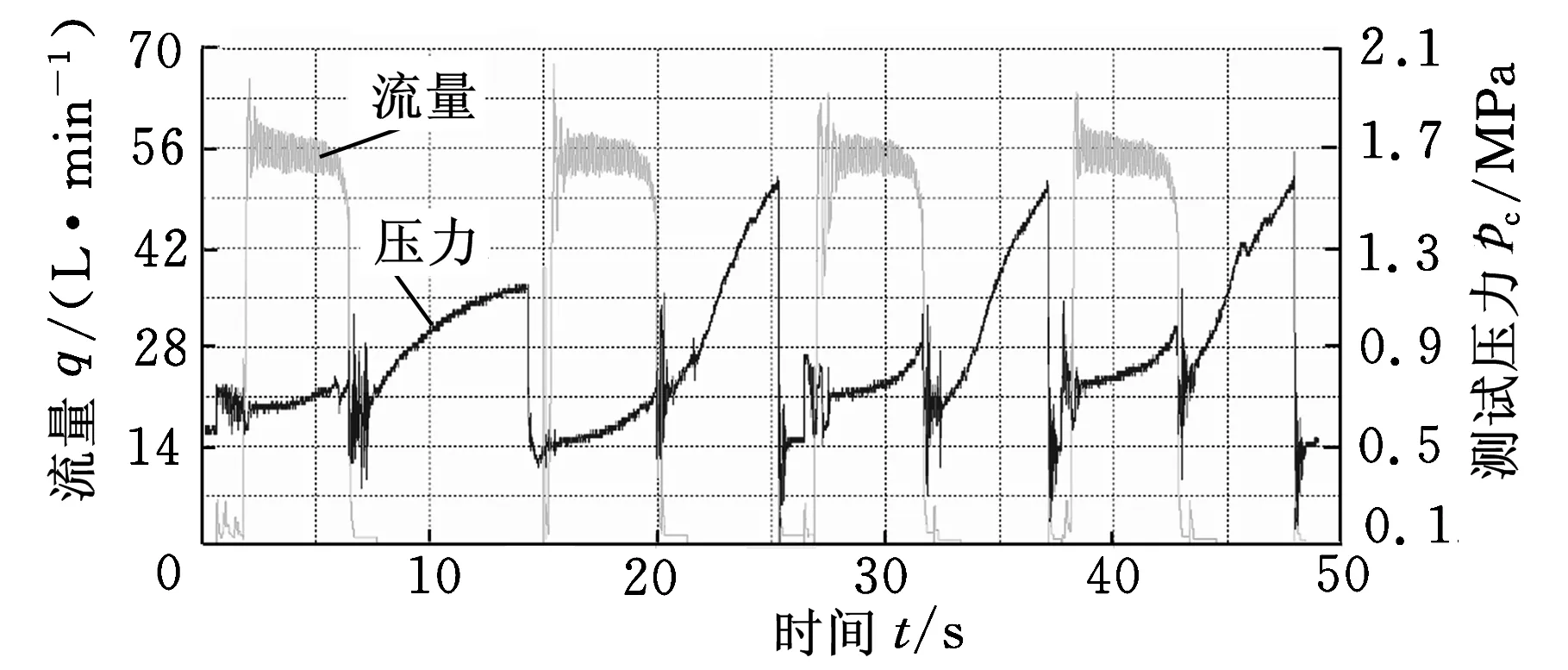
图7　铲斗油缸的测试压力和流量曲线

根据试验条件，输入方波振动控制信号,得到液压油缸的压力曲线如图8所示，从图8可以看出，铲斗油缸的最大压力为2.25MPa。实际上,铲斗油腔的压力还与液压油阻尼、管道长度以及连接机构的间隙等因素有关，受液压系统中泵功率恒定影响，理论计算的压力变化规律与实际测量值不同，铲斗油缸理论计算的最高压力与测试值基本接近，验证了流量振动控制的动力学模型的正确性。

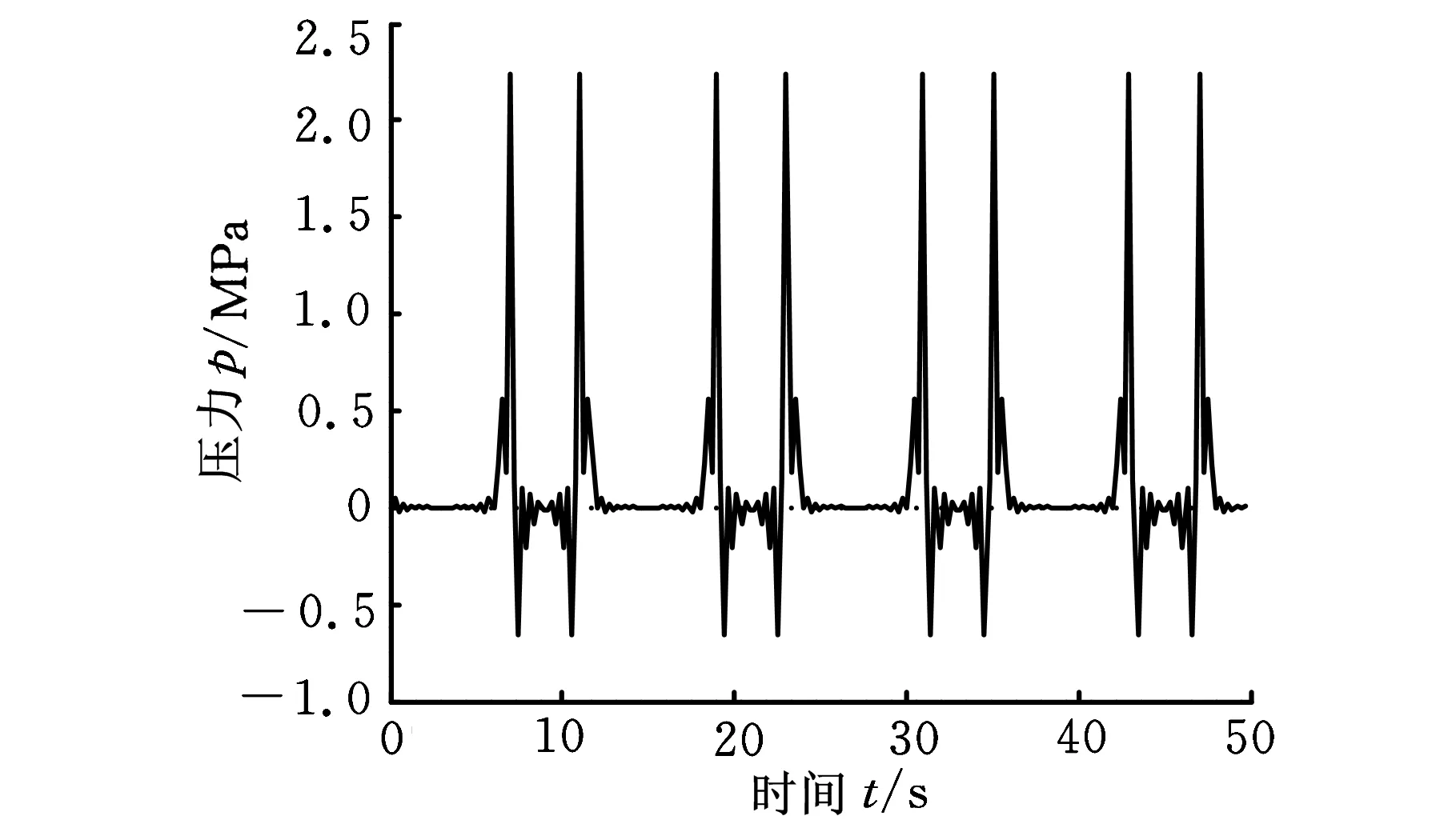
图8　铲斗油缸的模型计算压力

5　结束语

在流量振动控制信号中，利用傅里叶级数表示三角波、方波信号，解决了原始信号求导问题；采取流量控制方式时，应优先考虑方波信号，方波流量振动控制信号可获得较大的振动挖掘力，而正弦信号的振动挖掘力值最小，三角波介于两者之间；灵敏度系数、铲斗油缸压力的分析为振动挖掘控制参数的确定提供了理论依据。最后利用试验对流量振动控制模型进行了检验，验证了理论模型的正确性。

[1]朱建新,郭鑫,邹湘伏,等.岩土振动掘削技术研究现状及其发展趋势[J].工程机械,2006,37(1):33-38.

ZhuJianxin,GuoXin,ZouXiangfu,etal.ResearchSituationofVibratoryExcavationTechnologyforRockandSoilandItsDevelopingTrend[J].ConstructionMachineryandEquipment,2006,37(1):33-38.

[2]韩军,张德恩,杨宏,等.军用工程机械原理与技术[M]. 北京:国防工业出版社, 2011.

[3]郭鑫.液压挖掘机振动掘削减阻机理分析及参数优选[D].长沙：中南大学,2006.

[4]胡火焰.液压挖掘机铲斗振动掘削减阻及能耗机理研究[D].长沙：中南大学,2007.

[5]朱建新.液压挖掘机振动掘削机理及其过程优化建模与智能控制策略研究[D].长沙：中南大学，2008.

[6]SaqibGS,WrightME.VibratoryDiggersforHarvestingSweetPotatoesinCloddySoils[J].JournalofAgriculturalEngineeringResearch,1986,34(1):53-61.

[7]NiyamapaT,SalokheVM.LaboratoryInvestigationsintoSoilFailureUnderVibratoryTillageTools[J].JournalofTerramechanics,1993,30(6):395-403.

(编辑袁兴玲)

Analysis of Flow Control Parameters for Vibratory Excavation System

Han JunXiao WeiFeng JixinXu LiangGu Jun

The First Engineers Scientific Research Institute of the General Armaments Department,Wuxi,Jiangsu,214035

Flow control parameters play an important role in controlling excavating force and improving vibratory excavation effectiveness for different soil types.A kinematics model of multi mechanical linkages for vibratory excavation was established.Sensitivity coefficient relation between cylinder rod displacement and bucket tooth amplitude was derived,and solution method for vibratory excavation force and cylinder rod pressure was given.The key problems of square wave and triangular wave which could not be differentiated under normal conditions were solved using Fourier series in the flow control signals.The flow control parameters of waveform,sensitivity coefficient and pressure distribution were analyzed using numerical calculation.The vibration model of flow control was verified by tests.The results will provide theoretical basis for vibratory excavation control system development.

vibratory excavation;kinematics;excavation force;waveform;sensitivity

2014-04-14

TH113.1;O311DOI：10.3969/j.issn.1004-132X.2015.06.010

韩军，男，1966年生。总装工程兵科研一所研究员、博士。主要研究方向为机械振动与控制。专著2部,发表论文70余篇。肖伟,男,1976年生。总装工程兵科研一所工程师。冯继新,男,1972年生。总装工程兵科研一所高级工程师。徐亮,男,1979年生。总装工程兵科研一所工程师。顾俊,男,1985年生。总装工程兵科研一所工程师。