磁流变减振车刀模态仿真与实验研究

张永亮　潘健健　洪　明　张　玮

上海理工大学，上海，200093

磁流变减振车刀模态仿真与实验研究

张永亮潘健健洪明张玮

上海理工大学，上海，200093

针对车削加工过程中出现的刀具与工件之间的颤振，设计并研制了一种基于磁流变液挤压工作模式的减振车刀。为研究不同励磁电流下减振车刀的动态特性变化，通过类固体定义的方式在软件中定义磁流变液的参数，利用有限元仿真软件ANSYSWorkbench对减振车刀进行了模态仿真分析；通过设计的瞬态激振实验方案对减振车刀进行了模态测试实验。仿真与实验得出减振车刀的前4阶模态值。结果表明，随着励磁电流的增大，各阶模态值均增大，对应的刚度值也增大。

减振器；磁流变液；颤振；模态分析

0　引言

机床切削颤振是金属切削过程中刀具与工件之间产生的一种强烈的相对振动，它属于自激振动[1]。颤振会降低加工质量，影响加工精度，导致加工效率下降，因此研究抑制切削颤振的技术具有重要意义。智能材料磁流变液(magneto-rheological fluid,MRF)的出现为抑制切削颤振提供了新的方向。MRF在外加磁场下能在瞬间(毫秒级)从自由流动的液体变成类固体，呈现出可控的屈服强度，且这种变化是可逆的[2]。MRF现已在建筑、汽车等行业得到广泛应用[3]。在切削领域中，黄强等[4]通过研究认为，在切削加工中刀具系统为颤振的主体。孔天荣等[5]基于MRF的混合工作模式设计了一种智能镗杆，并取得了良好的减振效果。周渊等[6]将磁流变技术引入到车床中，设计了一种车床刀架磁流变减振器，进行了磁路的优化设计，并通过切削试验验证了该装置抑振的有效性。

有关磁流变减振器，多数学者进行的是动态试验分析。如孔天荣等[7]对磁流变镗杆进行了动态测试与分析，得到了镗杆刚度与阻尼变化规律；张天宇等[8]对所研究的磁流变阻尼器在不同激振频率下的阻尼特性进行试验研究。模态仿真分析的研究较少，主要是由于MRF独特的流变性能及测试方法的不完善，使得在有限元分析过程中难以准确定义其力学性能(刚度、阻尼等)。张挣鑫等[9]根据MRF具有的流体性和黏弹性，提出了一种重单元法，在ANSYS软件中模拟了MRF屈服前阶段的力学行为；王冬兵等[10]基于对MRF夹层简支梁的动力性能分析，将MRF夹层的有限元模型简化为梁单元模型考虑，最终建立了其有限元动力学矩阵方程，设置边界条件，解方程得到最终的动力学参数。

磁流变减振装置抑制颤振的本质是：不同电流下减振装置的模态参数会发生变化，从而改变系统的动态特性，抑制颤振。因此对磁流变减振装置在不同磁感应强度下的模态进行分析，可为后期有效抑制振动、寻找最佳颤振控制策略奠定基础。

本文通过类固体定义的方式定义MRF的材料参数，得到磁流变减振车刀前4阶的模态仿真值与振型。设计磁流变减振车刀的瞬态激振实验，得到前4阶的模态实验值。将仿真与实验结合得到了减振车刀的模态变化规律。

1　模态分析理论概述

模态分析的基本思想是，将描述结构的动态性能矩阵方程解耦,从而使N自由度系统的动力学特性可以用单自由度系统来表示。模态分析的核心内容是：确定描述结构系统动态特性的固有频率、阻尼比和振型等模态参数。通过模态分析，能够得到结构的固有频率和振型。将减振车刀看成一个多自由度的结构系统，其动力学方程可描述为

mx″(t)+cx′(t)+kx(t)=F(t)

(1)

式中，m、c、k分别为结构系统的质量、阻尼、刚度矩阵；F(t)为激励矢量；x(t)为位移矢量。

结构的固有频率由结构本身的属性决定，与外载荷无关。当无外载荷作用并忽略阻尼时，动力学方程可简化为

mx″(t)+kx(t)=0

(2)

假设系统做简谐振动，则有

x(t)=φsin(ωt+α)

(3)

式中，φ为特征矢量或振型；ω为角频率；α为初相角。

将式(3)代入式(2)，整理可得

-ω2m φsinωt+k φsinωt=0

(4)

式(4)在任意时刻t均成立，因此式(4)可简化为

(k-ω2m)φ=0

(5)

式(5)有非零解的条件是：(k-ω2m)是奇异的，即系数矩阵的行列式det(k-ω2m)有n个特征值wi(i=1,2,…,n)，wi即为系统的n个固有频率。将wi代入式(5)所求的φi即为振动频率wi下的振动型态。

2　磁流变减振车刀的三维结构设计及有限元模型

2.1三维结构

采用Solidworks对减振车刀进行三维建模，依次在Solidworks中建立减振器各零部件的三维立体模型，完成各个零部件之间的装配，并最终完成整个减振车刀的装配，如图1所示。磁流变减振车刀具体分为两大部分：一是主动部分，这部分包括自制车刀轴1和与车刀轴1之间过盈配合的左右铁芯6(励磁线圈5缠绕在铁芯上，共计4组)，这部分的运动是相同的，与车刀轴的运动一致；二是从动部分，包括了左端盖7、上下箱体以及嵌在下箱体8槽中的极板4，极板4是空套在车刀轴1上的，这部分的运动是一体的但不一定与车刀轴1的运动相同。励磁线圈5的另一端从上箱体(为显示减振车刀内部，将其隐藏，上箱体与下箱体8位置关于车刀轴线对称)的开口槽处引出，MRF从上箱体的开口槽中注入。在有限元分析中，许多学者将MRF用实体形式表示并对其动态特性进行研究，如胡白香等[11]在对MRF夹层简支梁的有限元分析中，将中间夹层MRF当作薄板来处理。磁流变减振车刀中，MRF存在于箱体和极板等之间的间隙间，在对间隙间的MRF进行三维建模时，间隙的初始距离即为薄板的厚度。

1.车刀轴　2.T形盘　3.磁流变液　4.极板　5.励磁线圈　6.铁芯　7.左端盖　8.下箱体图1　减振车刀的三维模型

2.2有限元模型及网格划分

将建立的减振车刀模型导入到Workbench中，在Workbench环境下完成对减振车刀的网格划分和材料定义。减振车刀中MRF的网格单元采用超弹性单元(HyPe-relastic8node185)定义，超弹性单元适用于承受大应变、大位移但体积改变极微小的材料(几乎不可压缩)。其余部分采用软件默认的网格单元solid186六面体单元定义，减振车刀有限元模型如图2所示，零件之间接触采用固结连接。边界条件决定各阶模态的形状，根据外圆车刀实际安装固定的方式，其边界条件设置为车刀柄的固定约束。

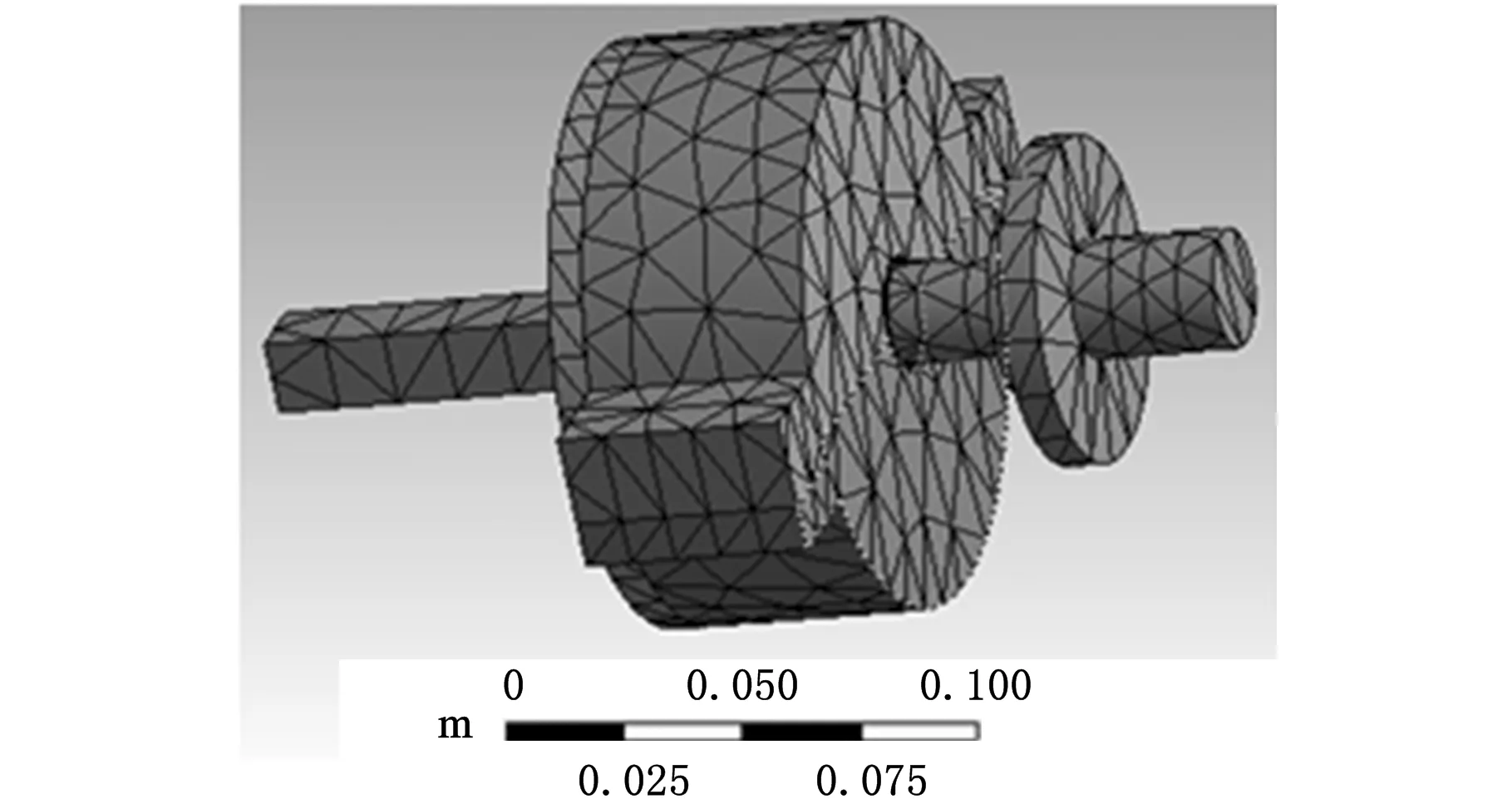
图2　减振车刀的有限元模型

3　磁流变液的定义

在进行模态仿真前，要对MRF进行参数定义。但由于MRF是一种新型的智能材料，故其性能参数如密度ρ、弹性模量E和泊松比μ等在目前Workbench材料库中还没有与之匹配的参数。

3.1复模量的确定方法

在进行减振装置模态仿真时，需对各组成材料的弹性模量进行定义。对于磁流变材料则需给出其复模量G*。复模量体现了材料应力-应变的关系，复模量G*的具体表达式为

G*=G′+iG″

(6)

其中，G′为储能模量，它与单位体积的材料在一定变形量时所储存的能量的平均值成正比，其实质等同于表述材料储存弹性变形能量能力的弹性模量；而G″为损耗模量，它与单位体积材料在同一周期变形后消耗的能量成正比。

减振车刀中的MRF在不同的磁场强度下会有不同的流变性质，因此会导致MRF的复模量等参数发生变化。Sun等[12]通过实验数据拟合出磁流变材料的储能模量和损耗模量与磁场的一组非线性关系:

G′=3.11×10-7B2+3.56×10-4B+5.78×10-1

(7)

G″=3.47×10-9B2+3.85×10-6B+6.31×10-3

(8)

式中，B为减振装置磁极间隙内的磁感应强度。

3.2磁场仿真

上述分析表明，只有确定了不同电流下减振装置磁极间隙内的磁感应强度，才能对MRF的复模量进行定义。因此本文采用电磁学仿真软件Maxwell，对装置内部在不同励磁电流下的磁感应强度进行模拟仿真。除了MRF的磁导率为非线性常数，采用手动输入外，组成减振装置的其他零件的磁导率均由软件直接提供。对三组不同的励磁电流(0.5A、1.0A、1.5A)下的磁感应强度进行仿真，得到相应的磁场仿真云图，见图3。

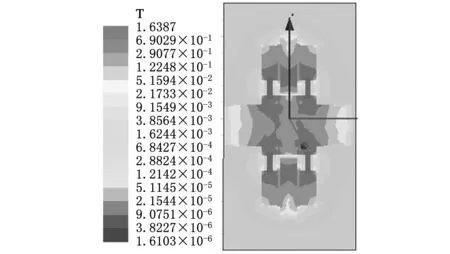
(a)励磁电流i=0.5 A

(b)励磁电流i=1.0 A

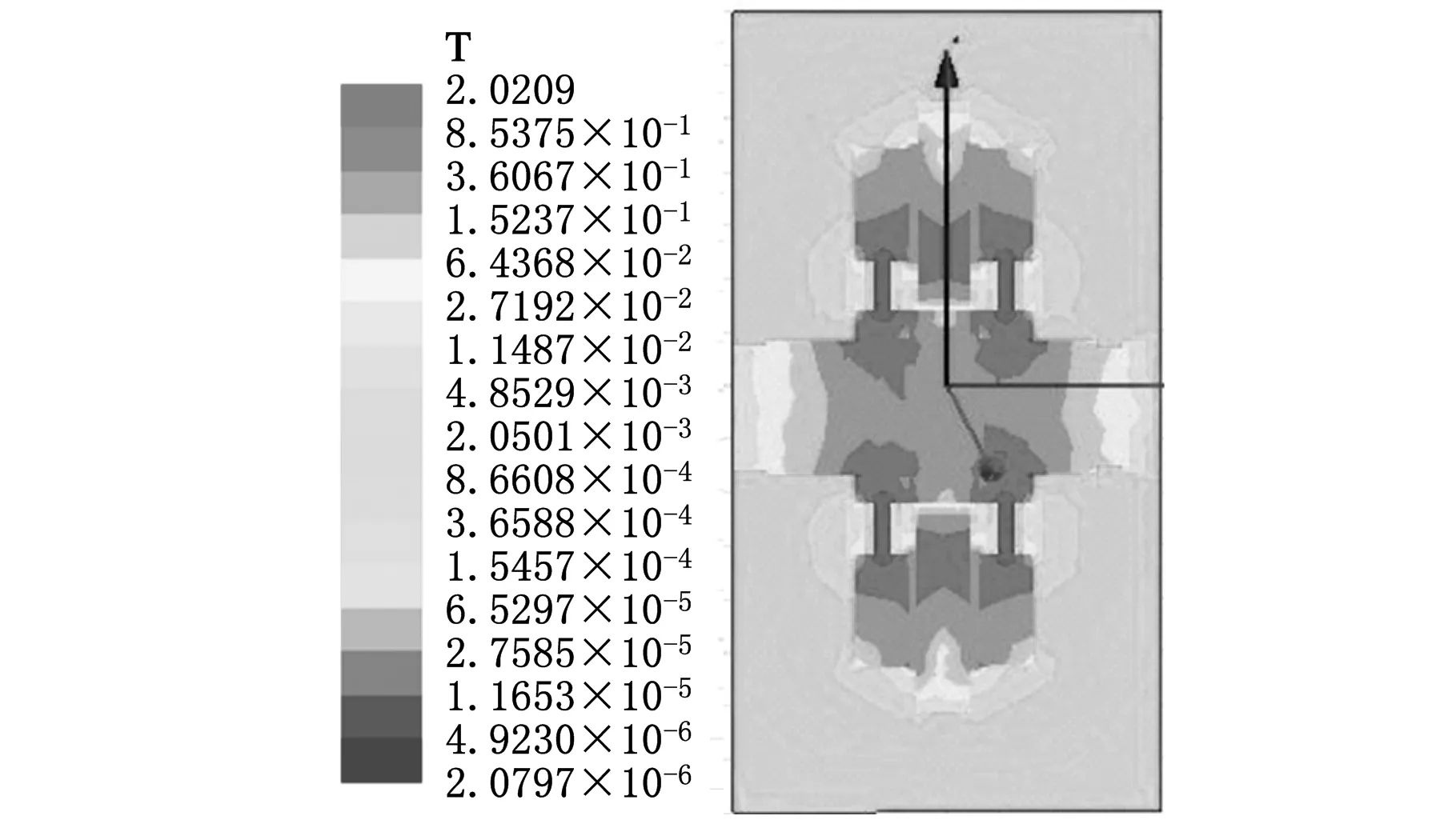
(c)励磁电流i=1.5 A图3　不同励磁电流下的磁感应强度

对图3所示磁感应强度云图中的数据进行提取，得到不同励磁电流下减振装置磁极间隙内的磁感应强度的平均值，如表1所示。

表1　不同励磁电流下的磁感应强度平均值

3.3MRF的仿真参数

由式(7)、式(8)可求出不同励磁电流下MRF的复模量，见表2。

表2　不同励磁电流下的复模量值

由Lord公司MRF产品的说明书可知，该MRF的密度为2650kg/m3。对于液体而言，泊松比一般为0.5，考虑到不同励磁电流下MRF流变性的变化，本文MRF的泊松比参考橡胶和尼龙的数值(分别为0.47和0.4)，取为0.45。

4　模态分析仿真结果

利用Workbench进行仿真，得到各阶模态参数，取不同励磁电流下前4阶模态的固有频率，如表3所示。根据振型动画，可知第1阶模态为水平摆动模态，第2阶模态为车刀的弯曲模态，第3阶模态为车刀绕轴线的扭转模态，第4阶模态为车刀的轴向压缩模态。对比表3中各阶模态的固有频率可知，随着励磁电流的增大，各阶模态的固有频率值增大，这说明随着MRF流变性质的改变，减振车刀的动态特性发生了变化，由此可以改变整个刀具系统的动态特性，达到消减切削颤振的目的。

表3　不同励磁电流下减振车刀的模态仿真值

5　磁流变减振车刀的模态参数测试实验

模拟切削加工工况，对磁流变减振车刀进行轴向的瞬态锤击实验，考察不同励磁电流下减振车刀各阶模态参数。

测试过程中，磁流变减振车刀安装在CA6140车床的方刀架上，在与车刀固定连接的圆盘上施加轴向的锤击激励。实验系统框图见图4。磁流变减振车刀励磁线圈的一端接入到直流电源中，调节直流电源可以对线圈励磁电流进行控制。加速度传感器安装在减振车刀前端的T形盘上，在瞬态激振实验过程中(实验现场如图5所示)，由加速度传感器采集到的振动信号先进入到NI数据采集卡中，然后在数据采集卡中经过数模转换等处理，最后处理信号进入到计算机中。最终采用专门的振动测试软件modal-view对信号进行分析，得到磁流变减振车刀拟合的模态曲线、各阶模态参数以及相应各阶模态下的振型，该过程使用到的仪器如图6所示。各阶模态的固有频率测试结果如表4所示。

图4　模态参数测试实验框图

图5　实验现场

图6　实验仪器

励磁电流(A)00.51.01.5第1阶模态频率(Hz)442448451.2458第2阶模态频率(Hz)453460461501第3阶模态频率(Hz)602611693705第4阶模态频率(Hz)816817832837

表4中数据揭示，随着励磁电流的增大，对应的同一阶模态下的频率值增大。由振型可知，前两阶模态对应的振型和数值与仿真中对应的是一致的，其振型分别为车刀水平摆动模态和弯曲模态。而实验模态中的第3阶模态为轴向伸缩振型，与仿真的轴向模态值相差较大(但亦保持随励磁电流的增大而增大的走势)。出现这种差异的原因如下：一是仿真过程中针对的减振对象为车刀，而实验中采集的数据来自车刀系统，车刀系统包括刀架、溜板箱等部分，车刀系统这部分是装配到一起的，容易发生振动，故实验模态数值较小；二是MRF是一种具有黏弹性特性的材料，在振动过程中，其黏性阻尼与振动的频率和温度等因素关系较大，而MRF这几种因素之间的具体联系目前的研究还较少，没有形成准确的理论，因此在仿真过程中，将MRF参数简化，未考虑其黏性特性。

6　结论

(1)对基于挤压模式的磁流变减振车刀进行模态分析，仿真得到减振车刀内部的磁感应强度，通过类固体定义的方式在软件中定义了MRF材料参数，并且采用超弹性单元定义MRF模型单元。

(2)通过模态仿真与实验对磁流变减振车刀进行了模态分析，得到减振车刀前4阶的模态频率值。结果均揭示，改变励磁电流的大小可以改变磁流变减振车刀的动态特性，随着励磁电流的增大，减振车刀的固有频率增大，可达到切削振动的抑制目的。

(3)实验与仿真的轴向模态频率值误差的产生是因为模态实验中测试对象为车刀系统，车刀系统轴向刚度较车刀的轴向刚度小，故实验模态频率值较小，且仿真过程中，将MRF参数简化，未考虑其黏性特性。

[1]王立刚，刘习军,贾启芬.机床颤振的若干研究和进展[J].机床与液压，2004(11):1-5.

WangLigang,LiuXijun,JiaQifen.StudiesandDevelopmentsaboutCuttingChatterofMachineTools[J].MachineTool&Hydraulics，2004(11):1-5.

[2]周云，谭平. 磁流变阻尼控制理论与技术[M]. 北京：科学出版社，2007.

[3]SinghAK,JhanS,PandeyPM.MechanismofMaterialRemovalinBallEndMagnetorheologicalFinishingProcess[J].Wear，2013,302：1180-1191.

[4]黄强，张根保，张新玉，等.对再生型切削颤振模型的试验分析[J].振动工程学报，2008,21(6):547-551.

HuangQiang,ZhangGenbao,ZhangXinyu，etal.ExperimentalAnalysisonRegenerativeChatterModel[J].JournalofVibrationEngineering，2008,21(6):547-551.

[5]孔天荣,李欣,梅德庆,等.磁流变智能镗杆的动力学模型[J].浙江大学学报(工学版)，2010,44(11)：2050-2055.

KongTianrong,LiXin,MeiDeqing,etal.DynamicModelofMagnetorheologicalIntelligentBoringBar[J].JournalofZhejiangUniversity(EngineeringScience) ，2010,44(11)：2050-2055.

[6]周渊，张永亮,刘军,等.一种剪切式磁流变车削减振器的设计与减振试验[J].振动与冲击，2013,32(4)：167-172.

ZhouYuan，ZhangYongliang，LiuJun,etal.DesignandTestofaShearTypeMRDamperforTurningVibrationSuppression[J].JournalofVibrationandShock，2013,32(4)：167-172.

[7]孔天荣,梅德庆,陈子辰.磁流变智能镗杆的动态特性测试与分析[J].浙江大学学报(工学版),2009,43(12)：2314-2318.

KongTianrong,MeiDeqing,ChenZichen.MeasurementandAnalysisofDynamicCharacteristicsofMagnetorheologicalIntelligentBoringBar[J].JournalofZhejiangUniversity(EngineeringScience), 2009,43(12)：2314-2318.

[8]张天宇.基于磁流变阻尼器的机床减振半主动控制[D].西安：西安科技大学，2007.

[9]张挣鑫，刘黔会,黄方林.一种在ANSYS中模拟磁流变液的方法[J].贵州大学学报(自然科学版),2011,28(4)：110-113.

ZhangZhengxin,LiuQianhui,HuangFanglin.AMethodtoSimulatetheMRFluidinANSYS[J].JournalofGuizhouUniversity(NaturalSciences),2011,28(4)：110-113.

[10]王冬兵.磁流变液夹层梁振动特性实验研究[D].镇江：江苏大学，2005.

[11]胡白香,夏品奇.磁流变夹层简支梁的有限元分析[J].工程力学，2007,24(9):95-99.

HuBaixiang,XiaPinqi.FiniteElementAnalysisofaSimplySupportMRFSandwichBeam[J].EngineeringMechanics，2007,24(9):95-99.

[12]SunQing,ZhouJinxiong,ZhangLing.AnAdaptiveBeamModelandDynamicCharacteristicsofMagnetorheologicalMaterials[J].JournalofSoundandVibration，2003，261(3)：465-481.

(编辑袁兴玲)

Modal Simulation and Experiment Based on MRF Damping Turning Tool

Zhang YongliangPan JianjianHong MingZhang Wei

University of Shanghai for Science and Technology,Shanghai,200093

Chatter occurred between the work-piece and tool during the turning process, a magneto-rheological damping tool was designed and developed based on the MRF squeeze mode. To study the dynamic change of the damping characteristics for different excitation currents, the parameters of MRF in the software was defined through entity definition. The modal analysis of damping device was simulated with ANSYS Workbench. Also the transient excitation modal testing platform was built for the modal experiments. The first four modal data of the simulation and experiments were presented. Results show that with the increase of the excitation current, the modal values increase so as the stiffness values.

damper;magneto-rheological fluid(MRF); chatter; modal analysis

2014-07-25

TH12< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.07.008

张永亮，女，1973年生。上海理工大学机械工程学院副教授、博士。主要研究方向为机械动力学及加工精度、智能材料切削减振技术。潘健健，男，1987年生。上海理工大学机械工程学院硕士研究生。洪明，男，1988年生。上海理工大学机械工程学院硕士研究生。张玮，女，1988年生。上海理工大学机械工程学院硕士研究生。