混沌野草扩展Kalman滤波器辨识六维力传感器下E膜模型参数

朱文超　许德章

安徽工程大学，芜湖，241000

混沌野草扩展Kalman滤波器辨识六维力传感器下E膜模型参数

朱文超许德章

安徽工程大学，芜湖，241000

为解决动载环境下噪声污染导致六维力传感器测量精度急剧下降，以及扩展卡尔曼滤波器难以获得最优系统干扰矩阵的问题，提出了一种基于混沌野草算法优化的扩展卡尔曼滤波(CIWO-EKF)算法。根据挠度与应变之间的关系，构建了六维力传感器下E膜非线性模型。基于野草繁殖算法，以前6阶主振型信息构成的系统干扰阵为均值进行高斯采样，产生初始化的可行解。将混沌搜索技术与野草算法相融合，利用野草算法进行全局搜索，通过混沌序列对群体中适应度高于平均值的个体执行给定步数的局部搜索，指导种群向最优解方向逼近，避免搜索过程陷入局部最优。采用改进的野草算法对扩展Kalman滤波中的系统干扰矩阵进行优化处理。仿真实例表明，改进扩展卡尔曼滤波器在提高六维力传感器测量精度的同时，可以保持较好的稳定性和鲁棒性。

六维力传感器；下E膜；混沌野草算法；混沌序列；扩展卡尔曼滤波器

0　引言

相对于压电式力传感器，电阻应变片式力传感器在精度、可靠性等方面具有明显优势，因而获得广泛应用。电阻应变片式六维力传感器的测量原理是弹性梁在被测力作用下产生变形，贴在弹性体上的应变片阻值发生变化，通过惠斯顿电桥获得力信息电信号。双E弹性体六维力传感器采用组合梁结构来探测空间6个方向的力和力矩[1]。由于电阻应变片热噪声、放大电路以及电路周围的电磁干扰源等原因，导致原始信号在传输、转换、采集过程中不可避免地混入噪声信号，严重地影响了传感器的测量精度，因此，实时有效地滤除噪声在传感器研究中具有重大意义，同时也是难点之一。

通过分析有用信号的规律性、噪声信号随机性特征，采用合适的统计学最优估计算法滤除噪声信号是现代信号处理技术的热点之一。扩展卡尔曼滤波(extended Kalman filtering，EKF)运用自回归方法计算非线性系统状态和参数的估计值，它能够根据观测信息获得最小均方误差意义下的最优估计[2]。然而，系统测量干扰矩阵的准确性在很大程度上决定了EKF的滤波精度和稳定性。噪声矩阵的不合适导致系统的不确定性增加，最终使EKF的性能下降[3]。关于如何选择EKF的最优噪声矩阵，国内外学者进行了许多尝试与探索。应用最广的辨识算法是试探法[4]，但该算法耗时较多，并且过分依赖模型的先验信息及个人经验。文献[5-6]利用遗传算法优化交流异步电动机模型及与其具有耦合关系的锂离子动力电池等效电路模型扰动矩阵，实现了对电机转子转速的实时估计，能满足电动车辆仿真精度要求。然而遗传算法收敛速度较慢，稳定性较差，局部搜索能力较弱。文献[7]利用粒子群优化算法对定子磁链系统噪声矩阵进行优化，提高了系统低速控制性能，然而粒子群算法容易早熟，不能有效地跳出局部最优。

为解决传统优化算法局部搜索能力弱、收敛速度慢、对初值选取异常敏感的问题，本文提出了一种基于混沌野草算法优化(chaotic invasive weed optimization,CIWO)的扩展卡尔曼滤波算法，即CIWO-EKF算法。根据下E膜受迫振动的正弦激励力响应与薄板应变的关系，建立了有色噪声状态空间模型，按照固有频率值对所有薄板主振型进行排序，基于野草繁殖思想，选取前6阶主振型作为均值，通过高斯采样产生初始解。采用野草算法进行全局搜索，通过混沌序列进行局部搜索，提高收敛速度，避免迭代过程陷入局部最优。

1　双E弹性体六维力传感器下E膜系统模型

1.1双E弹性体六维力传感器的结构

1.外传力环　2.内传力环　3.矩形薄板　4.上E膜5.中心传力环　6.下E膜　7.底座图1　双E弹性体六维力传感器结构

本文以双E弹性体六维力传感器为研究对象，其结构如图1所示，传感器主要由上E膜4、下E膜6、薄板3和底座7组成。上下E膜与中心传力环5相连，上E膜周围设置内传力环2，并通过4个矩形薄板连接外传力环1。其中，上E膜用于检测力矩MX、MY，下E膜用来检测切向力FX、FY和法向力FZ，矩形梁用来检测力矩MZ。传感器材料为LY12，弹性模量为72 GPa，密度为2700 kg/m3，泊松比为0.33。1.2下E膜系统状态模型

当传感器受法向力FZ作用时，外力通过中心传力环传递到下E膜，其受力情况以及电阻应变片布置位置如图2所示。考虑下E膜的力学模型，定义其边界条件为外边界固定、内边界受到正弦激励力作用。

图2　下E膜受力分析

基于模态叠加理论，结合零初始条件，下E膜对正弦激励力的响应(即下E膜受迫振动的动挠度)可按极坐标系下的主振型函数与反映其运动规律的时间函数展开为以下无穷级数[8]：

(1)

Wj(r,φ)=[Dj1Jn(λ r)+Dj2Yn(λ r)+

Dj3In(λ r)+Dj4Kn(λ r)]cosn φ

(2)

Kj(r,φ)=2πK[Dj1J0(λjri)+Dj2Y0(λjri)+

Dj3I0(λjri)+Dj4K0(λjri)]

(3)

根据零初始条件下，下E膜对正弦激励力的响应w(r,φ,t)与径向应变ε(r,φ,t)之间的关系，N阶固有频率下六维力传感器下E膜的非线性离散时间系统状态方程可表示为

(4)

式中，Nj为电阻应变片质心系数；ε(k)为薄板随时间变化的应变函数；k为时间；T为采样周期；h为薄板的厚度。

Xk+1=Φk+1,kXk+Gk+1,kUk+Γk+1,kηk

(5)

Zk+1=H Xk+1+Vk+1

(6)

Uk=[KsinwkI]T

其中,Xk+1为k+1时刻状态变量；Uk为系统控制矢量；ηk为白噪声序列；H为测量系数矢量；Zk+1为k+1时刻观测值；I为单位矩阵；Ks为应变片灵敏系数；c为各阶主振型的幅值比；测量噪声Vk+1是均值为0、方差为Rσ的高斯白噪声序列。系统状态转移矩阵、系统控制项系数矩阵、系统干扰系数矩阵分别为

Γk+1,k=

其中，噪声系数A、B、C、D根据噪声模型的复杂度进行选择，一般取A,B,C,D∈[1,5]。零均值白噪声序列ηk的协方差矩阵为

(7)

(8)

1.3下E膜扩展卡尔曼滤波器

基于极大后验估计原理，利用次优无偏自适应滤波器[10]对未知时变的测量噪声协方差R进行实时估计，结合传统EKF算法，得到六维力传感器下E扩展卡尔曼滤波器，具体迭代步骤如下。

(2)预测阶段:

(9)

(10)

(3)更新阶段:

(11)

Kk+1=Pk+1,kHT(HPk+1,kHT+Rk+1)-1

(12)

(13)

Pk+1=(I-Kk+1H)Pk+1,k

(14)

在噪声协方差矩阵有误差的情况下，设Qchoice、Qtrue分别为不对主振型进行全部分析的情况及理想状态下选取的系统干扰协方差矩阵，Rchoice、Rtrue分别为不对所有测量噪声类型进行全部分析的情况及理想状态下的测量噪声协方差矩阵，若Qchoice≠Qtrue，Rchoice≠Rtrue,则后验误差P>Ptrue[11]，其中，Ptrue为理想状态下的后验误差。在六维力传感器EKF滤波器中，测量噪声协方差R可以通过极大后验算法实时估计。然而，若想获得全区间精确的系统干扰协方差矩阵Qn，则需要对所有主振型进行分析。为了解决这一问题，本文拟通过适当调整Qchoice,使其无限接近于理想的噪声矩阵Qtrue，从而保证EKF滤波器在规定的误差范围内很好地工作[12]。然而，若Qchoice的调整幅度不当，易导致滤波器瞬态特性加快、状态量修正缓慢、滤波器稳定性受阻。故为了保证估计误差渐进收敛，实现最优滤波，系统干扰协方差矩阵Qn的选取十分重要。

2　混沌野草算法优化EKF系统干扰矩阵

2.1标准野草算法

野草算法[13](invasive weed optimization, IWO)是基于种群的数值优化计算方法，其执行过程是模拟野草克隆的自然繁殖过程，对于处理复杂和非线性规划问题有着很好的效果。具体实现步骤如下：

(1)种群初始化。一定数目的野草以随机方式在空间扩散分布，一般情况下，初始种群中的野草个数可根据实际问题进行调整。

(2)生长繁殖。各株野草所产生的种子个数为

(15)

式中,f为当前野草的适应度值; fmax、fmin分别为当前种群中野草对应的最大适应度值和最小适应度值; smax、smin分别为每株野草所能产生种子的最大值和最小值。

(3)空间扩散。野草子代个体(种子)以均值为 0、标准差为σ正态分布方式扩散在L维空间中。种子的产生是通过野草在每一维加上变化区间步长H得到的，H∈[-σ,σ]，迭代过程中，每一代的标准差σcur变化规律如下：

(16)

式中，I为当前进化代数;Imax为最大进化代数;σinit、σfinal分别为标准差的最初值和最终值;u为非线性调和因子。

(4)竞争性生存。只有具有较好适应性的野草个体能生存并产生种子，其他则消亡。

2.2混沌法

混沌是非线性动力系统中的固有特性，是非线性系统中普遍存在的现象。本文选取Logistic映射作为混沌系统[14]：

ym+1=μ ym(1-ym)0≤y0≤1

(17)

其中，μ为控制参数，m为迭代次数，当μ∈{3.57,4}且y0∉{0,0.25,0.5,0.75,1}时，Logistic映射产生的序列呈现出混沌的动态特征，方程值的变化周期无限大，初始变量的微小变化将导致后续轨道的巨大不同。此时利用混沌运动的特性可以进行优化搜索。优化搜索的基本思想是按照下式:

y1,k=(xk-xmin)/(xmax-xmin)

(18)

将优化变量xk映射为Logistic方程定义域[0,1]之间的混沌变量y1,k，由式(17)迭代产生与待优化变量数目相同的一组混沌序列yk，将其通过下式:

(19)

2.3混沌野草算法优化EKF系统干扰矩阵

下E膜的系统干扰系数矩阵有6个变量，每个变量都与振型函数的阶数有关，即

Qn=diag(Q11,Q22,…,Q66)n=1,2,…,N

(20)

系统干扰矩阵的优化，就是在每个采样周期对以上 6个元素进行调整。每株野草对应一组参数，每次迭代后计算相应的系统输出及其适应度值，选取适应度好的前Pmax株野草，淘汰其余的个体。多次迭代后将获得的全局最优值作为噪声矩阵参数Qbest。CIWO通过适应度函数来确定各株野草的优劣，在六维力传感器滤波估计中，EKF滤波器对噪声矩阵的优化是以实际输入正弦信号曲线与最优估计反馈信号曲线的拟合均方误差最小为目标的，因此，CIWO的适应度目标函数定义如下:

(21)

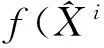
主振型信息主要分布在系统模型中状态转移项、控制项以及系统干扰项中；由于高阶主振型对应的固有频率值(7阶固有频率已达54 611 Hz)远远大于正弦激励力频率(200～2000 Hz)，故它们在各项系统参数中的权重非常小，则不难想象，最优系统干扰信息主要分布在低阶主振型中。

(1)设定初始信息：最大种群规模Pmax，最大、最小迭代次数Imax、Imin的值。

(2)根据式(16) 计算每代种子的变化区间步长σcur。

(3)利用适应度目标函数(式(21))计算种群中父代野草的适应度值Fi，由式(15) 计算子代种子的个数，产生种子按照均值为 0、标准差为σcur的正态分布方式扩散。

(4)判断种群的规模是否达到最大种群规模Pmax，如果达到，则计算种群的所有野草和种子的适应度值，并进行排序。由高到低，分别选取n个个体作为下一代的野草。否则转步骤(2)。

(6)判断算法是否达到最大迭代次数Imax，如果达到，输出最优解; 否则执行步骤(2)。

3　六维力传感器动态耦合特性研究

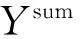
图3　六维力传感器动态耦合特性

阶跃或冲击激励虽然操作简便，对实验设备要求不高，但存在很大的局限性，主要表现如下：①只能在时域内测量传感器的输出；②难以精确获得多维力传感器在整个使用频带范围内的传输特性；③获得完全意义上的脉冲力或阶跃力比较困难，测量精度较低。

动态耦合误差补偿机理和方法、动态解耦算法是后续研究需要解决的问题，故本文只讨论单方向激励情况下E膜的输出信号滤波问题。

4　六维力传感器下E膜滤波实例

4.1六维力传感器动态测试系统

六维力传感器动态测试系统主要由数据分析PC机、动态标定实验台、虚拟仪器NI-PXI-1042Q、控制器PXI-8196、板卡PXI-4461、放大电路和压电陶瓷驱动模块等部分组成，如图4所示。测试系统的工作原理如下：将双E弹性体六维力传感器(图5)固定在动态标定实验台上，选择压电陶瓷驱动模式，产生幅频可调的正弦激励力信号；通过转接板加载在传感器上，输出的6路信号经过放大电路增幅和缓冲后被虚拟仪器的数据采集模块(板卡PXI-4661)高速采集；利用信号调理模块(控制器PXI-8196)对采集数据进行实时处理，并将其导入PC机中的LabView环境下进行分析。

图4　动态测试系统

图5　双E弹性体六维力传感器

4.2正弦激振信号分析

实验选用XMT压电陶瓷驱动器(图6)产生标准正弦信号，并可通过仪器上的按键来实现正弦波信号的变幅变频。该驱动器的具体工作过程如图7所示。信号发生器产生幅频可调的正弦信号，经过12位D/A转换后，输出的模拟信号被驱动器功率放大，从而驱动压电陶瓷，最终加载到六维力传感器上。然而，D/A转换器的分辨率问题，导致电路实际输出的模型电压值和理论输出不同。对12位D/A转换的精度q进行计算：

(22)

式中,VREF为D/A转换器的参考电压；b为D/A转换器的位数。

图6　XMT压电陶瓷驱动器

图7　压电陶瓷驱动模式

驱动器中的12位D/A转换器精度为0.0122%，转换误差较小，分辨率较高，故在六维力传感器数字滤波过程中，可以忽视D/A精度和机械系统误差等造成的损失，并近似地将模拟信号视为理想控制信号波形。

4.3下E膜数学模型

下E膜的结构尺寸如下：内半径为50 mm，外半径为100 mm，板厚h为2 mm。4枚电阻应变片质心的位置参数分别为rx1=rx4=40mm；rx2=rx3=20mm；φx1=φx2=π/4；φx3=φx4=5π/4；取收敛系数A=0.05，C=B=0.5；应变片灵敏系数Ks=1.4，初始阻值R=50Ω；正弦激励力的幅值K=20；激振频率w=200Hz；根据下E膜前6阶主振型相应的参数(表1)求得幅值比c=3.9009，固有频率系数λ1=99.3966,λ2=184.648，结合电阻应变片X1的相关信息，获得下E膜量测数学模型：

(23)

Zk+1=[-4.301100]Xk+1+Vk+1

(24)

零均值白噪声序列ηk未优化前的协方差阵为

Q6=diag(-5.64×10-3，-5.4749×10-3，0.4892×10-7，

-5.5863×10-7，8.3563×10-7，-3.4643×10-7)

表1　前6阶有频率与振型振幅函数

4.4信号滤波实验

采集传感器空载输出的6路时域数据，分析其规律，获得测量噪声初始方差值R0。设置采样频率为20Hz，随机从时域数据集中取出50个采样值；依次利用遗传算法(GA)、粒子群算法(GSO)和混沌野草算法(CIWO)优化EKF中的系统干扰矩阵。遗传算法、粒子群算法与野草算法的具体参数见表2。三种算法优化后的系统干扰协方差Qn见表3。图8所示为三种算法优化EKF系统干扰矩阵的适应度函数收敛曲线。从图8可以看出，CIWO的收敛速度较快，稳定适应度函数值较低，最优解优于GA和GSO。

表2　IWO与GA的初始参数

表3　三种算法的优化结果

图8　适应度函数

为了更加有效地检测算法的滤波性能，本节在假定三种正弦波激励的情况下，考察GA、GSO、CIWO三种算法对EKF的系统干扰矩阵的优化效果(采样时间间隔为0.05 s)：

(1)固定幅频的正弦激励力。选择固定幅值为10、激振频率为100 Hz的正弦激励力作为FZ方向的加载力，图9所示为三种算法优化的EKF滤波效果曲线。CIWO的滤波效果较好，状态参量浮动程度较小，稳定性较高。从表4的均方误差值中可以看出，采用CIWO优化的EKF滤波精度比GA提高了60.53%，比GSO提高了33.72%。

(2)幅值扰动、激振频率不变的正弦激励力。为了验证三种算法优化下EKF的鲁棒性，假设第26次采样正弦激励力的幅值从5 mA跃变为8 mA。图10所示为系统突变前后三种算法优化的EKF滤波效果曲线。可以看出，在正弦激励幅值扰动的状态下，与其他两种优化算法相比，CIWO-EKF滤波精度较高，均方误差小，鲁棒性更强。

图9　固定幅频激励下的滤波效果

mV

图10　幅值扰动情况下的滤波效果

(3)激振频率扰动、幅值不变的正弦激励力。假设第26次采样时正弦激励力的激振频率从100 Hz跃变为120 Hz。在正弦激励频率扰动的情况下，系统控制项系数以及噪声系数相应地改变，导致系统状态以及测量值从第26次采样时开始发生突变。图11所示为系统突变前后三种算法优化的EKF滤波效果曲线。基于CIWO优化EKF可以精确地跟踪系统突变状态，其鲁棒性优于其他两种算法，在系统突变的前后，可以更快地趋于稳态。

图11　激振频率扰动情况下的滤波效果

(4)运算复杂度评价。图9～图11以及表4记录了三种算法在相同迭代次数下的滤波精度以及状态估计均方误差。CIWO的滤波效果及鲁棒性明显高于GA与GSO。但评价算法优劣的最重要的特性就是运算复杂度，高精度高耗时的算法同样不适合处理实际问题。为此，本文在相同均方误差的前提下，评价三种算法的迭代次数与运算时间，以GA的均方误差1.9504×10-3、2.2356×10-3、2.3131×10-3为基准，见表5。

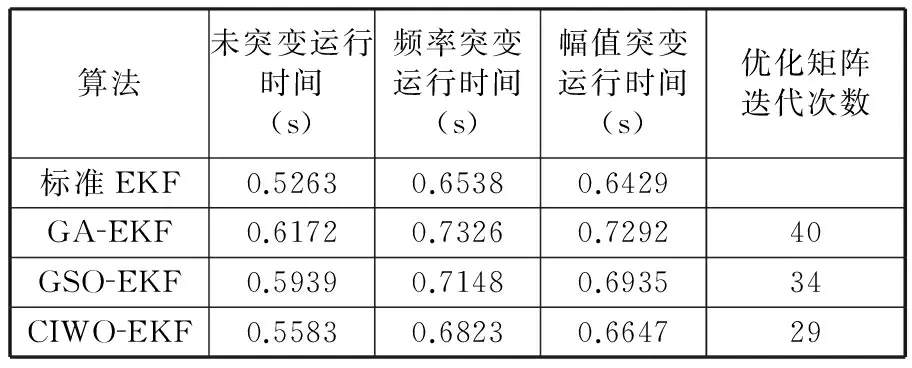
表5　三种滤波算法的运行时间

从表5可以看出，虽然三种算法同时对系统干扰协方差进行了优化，但CIWO-EKF的计算耗时明显少于前两种算法。与标准的EKF相比，本文算法的平均运行时间并没有明显的增加，在提高六维力传感器量测精度的同时，可以保持其实时性。

5　结语

为减小噪声信号对六维力传感器测量精度的影响，同时解决扩展 Kalman 滤波器难以获得最优系统干扰矩阵的问题，本文提出了一种混沌野草算法优化的扩展卡尔曼滤波算法(CIWO-EKF)。算法根据正弦激励力响应和应变的关系，基于时间序列法，采用等效的高斯-马尔可夫模型对系统干扰进行白化处理，得到下E膜有色噪声增广状态模型。为了获得系统最优估计，在野草繁殖算法的基础上，融入混沌搜索技术，利用混沌序列较强的局部搜索能力，增强野草算法的局部寻优能力。采用改进野草算法对EKF中的系统干扰矩阵进行优化处理，并将改进的EKF在六维力传感器动态测试系统中进行仿真研究。仿真实验表明，与遗传算法和粒子群算法相比，CIWO-EKF滤波精度较高，趋于稳态的速度较快。在正弦激励力参数存在扰动的情况下，能准确地跟踪突变状态，具有较好的鲁棒性。在多方向激励力情况下，六维力传感器下E膜滤波算法还有待进一步深入研究。

[1]梁康桥.特殊应用的多维力/力矩传感器研究与应用[D].合肥：中国科学技术大学，2009.

[2]Rigatos G G.Extended Kalman and Particle Filtering for Sensor Fusion in Motion Control of Mobile Robots[J].Mathematics and Computers in Simulation, 2010,81(3):590-607.

[3]Rigatos G G.Nonlinear Kalman Filters and Particle Filters for Integrated Navigation of Unmanned Aerial Vehicles[J]. Robotics and Autonomous Systems, 2012,60(2):978-995.

[4]Shi Keli, Chan T F, Wong Y K,et al. Speed Estimation of an Induction Motor Drive Using an Optimized Extended Kalman Filter [J].IEEE Transactions on Industrial Electronics, 2002,49(1):124-133.

[5]张彩萍，姜久春. 用基于遗传优化的扩展卡尔曼滤波算法辨识电池模型参数[J].吉林大学学报(工学版)，2012,42(3):732-737.Zhang Caiping, Jiang Jiuchun.Extended KalmanFilter Algorithm for Parameter Identification of Dynamic Battery Model Based on Genetic Algorithm Optimization[J].Journal of Jinlin University(Engineering and Technology Edition), 2012,42(3):732-737.[6]张勇军，王京，李华德.基于遗传算法优化的定子磁链扩展卡尔曼估计方法[J].电工技术学报，2009，24(9):64-69.

Zhang Yongjun, Wang Jing, Li Huade. A Method of the Stator Flux EKF Estimation for Induction Motors Based on Genetic Algorithm Optimizing[J]. Transactions of China Electrotechnical Society, 2009，24(9):64-69.

[7]林国汉，章兢，刘朝华，等. 改进粒子群算法优化扩展卡尔曼滤波器电机转速估计[J].计算机应用研究，2013，30(7):2003-2006.

Lin Guohan, Zhang Jing, Liu Zhaohua,et al.Speed Estimation of Motor Using Improved Particle Swarm Algorithm Optimized Extended Kalman Filter[J]. Application Research of Computers, 2013，30(7):2003-2006.

[8]Xu Dezhang, Wang Zhihong.Free Vibration Analysis of Elastic Bodies for Six-axis Force Sensor[J].Journal of Sensor Technology, 2013,3(1):13-20.

[9]汪志红.电阻应变片式六维力传感器弹性体力学特性的研究[D].芜湖：安徽工程大学，2013.

[10]杨元喜,任夏，许艳.自适应抗差滤波理论及应用的主要进展[J].导航定位学报,2013,1(1): 9-13.

Yang Yuanxi,Ren Xia,Xu Yan.Main Progress of Adaptive Robust Filter with Application in Navigation[J].Journal of Navigation and Positioning, 2013,1(1): 9-13.

[11]付梦印,邓志红. Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2010.

[12]Ligorio G,Sabatini A M.Extended Kalman Filter-based Methods for Pose Estimation Using Visual, Inertial and Magnetic Sensors: Comparative Analysis and Performance Evaluation[J].Sensors,2013,13(2):1919-1941.

[13]张氢，陈丹丹，秦仙蓉，等.杂草算法收敛性分析及其在工程中的应用[J].同济大学学报(自然科学版)，2010，38(11): 1689-1693.

Zhang Qing, Chen Dandan, Qin Xianrong,et al. Convergence Analysis of Invasive Weed Optimization Algorithm and Its Application in Engineering[J]. Journal of TongJi University(Natural Science),2010,38(11):1689-1693.

[14]纪震，廖惠连，吴青华.粒子群算法及应用[M].北京：科学出版社，2009.

[15]许德章，吴仲城，葛运建，等.机器人六维腕力传感器耦合矩阵的确定与摄动分析[J].仪器仪表学报，2005，26(1)：75-81.

Xu Dezhang, Wu Zhongcheng, Ge Yunjian.The Solution to and the Analysis with Cross-coupling Matrix of Six-axis Wrist Force Sensor for Robot[J].Chinese Journal of Scientific Instrument, 2005,26(1):75-81.

[16]Liu Zhengshi, Wang Yong, Chen Enwei,et al.A Method for Measuring DynamicPerformance Index of Robots Multi-axis Wrist Force Sensor[C]//Proc. IEEE Int. Conf. on Information Acquisition. Hong Kong&Macau,2005:170-176.

(编辑陈勇)

Model Parameter Identification for a Lower E-type Membrane of Six-axis Force Sensor Based on CIWO-EKF

Zhu WenchaoXu Dezhang

Anhui Polytechnic University，Wuhu，Anhui，241000

The measurement accuracy of a sensor which worked on the environment of the dynamic load could be seriously affected by the pollution of noise signals and the EKF could not gain the optimal system noise matrix. A new EKF based on CIWO was proposed. The nonlinear state-space model was established based on the relationship between the deflection and the strain. The idea of the grass breeding was introduced to achieve the Gauss sampling of system interference matrix consisted of first six-order vibration mode informations and to produce the initial feasible solutions. After combining chaotic search technology with invasive weed optimization (IWO), the global search of the new algorithm was executed by the IWO. Then the chaotic sequences executed the local search to the individual which had the higher fitness value than average and guided the population approaching to the optimal solution. The search process can be avoided to fall into local optimum. Finally, the improved invasive weed optimization algorithm was introduced to optimize the system’s noise matrix in EKF. The simulation results indicate that the new algorithm can enhance the measurement accuracy of six-axis force sensor effectively and maintain better robustness and real-time performance.

six-axis force sensor；lower E-type membrane；chaotic invasive weed optimization(CIWO)；chaotic sequence；extended Kalman filtering(EKF)

2013-09-25

国家自然科学基金资助项目(51175001)；安徽省自然科学基金资助项目(11040606M144)

TH73DOI：10.3969/j.issn.1004-132X.2015.07.005

朱文超，男，1989年生。安徽工程大学机械与汽车工程学院硕士研究生。主要研究方向为机器人信息感知。许德章，男，1964年生。安徽工程大学机械与汽车工程学院教授、博士。