切向载荷下螺栓结合部静特性分析及试验

惠　烨　黄玉美　李　艳

1.西安理工大学教育部数控机床及机械制造装备集成重点实验室，西安，7100482.陕西科技大学，西安，710021

切向载荷下螺栓结合部静特性分析及试验

惠烨1,2黄玉美1李艳1

1.西安理工大学教育部数控机床及机械制造装备集成重点实验室，西安，7100482.陕西科技大学，西安，710021

为了准确理解螺栓结合部静态特性，基于结合面基础特性建立了螺栓单元结合面解析数学模型，提出了一种等效分步载荷解析算法，可以实现在结合部承受切向载荷时，无需考虑载荷间耦合关系就能对结合部力平衡非线性隐含积分方程组进行快速准确求解。采用自行设计的螺栓结合部切向加载装置进行了结合部扭转和剪切加载试验。试验与解析结果均表明，在切向载荷不超过最大静摩擦力的情况下，螺栓结合面切向变形与外载荷成线性关系。解析与试验结果的一致性验证了模型的正确性，为机械结合面静态特性分析提供了理论和试验支持，求解算法可方便地将结合面研究成果应用于工程实践。

螺栓结合部；静特性；切向载荷；分步计算

0　引言

为了便于加工制造、运输以及满足功能方面的要求，复杂机械产品由许多零部件按照一定的功能要求组合起来，零部件间不可避免地形成了大量的结合部[1]。研究表明，机床的静刚度中30%～50%取决于结合部的刚度特性，机床出现的振动问题有60%以上源自结合部[2]。结合部的特性可以用结合部接触表面的结合面描述，零件间结合面作用机理非常复杂，多为非线性因素，与零件的材料、加工方法、形状及装配、调整等都有相当大的关系[3-5]。从微观上看，两个结合面在相接触时只有微小的凸起接触，表现出的接触特性与零件本体有着明显的不同[5]。

螺栓连接具有良好的装调和拆卸维修性能，在航空发动机、数控机床等机械中，连接螺栓的数量庞大[6]，形成大量的螺栓结合部。螺栓结合部是平面结合部和螺纹结合部位组成的复杂结合部[7]，具有很强的非线性特性，研究其静态特性建立模型至关重要。杨国庆等[8]结合有限元分析及插值计算方法对螺栓连接的被连接件刚度计算方法进行了研究，并采用I-Scan压力测量系统测得了被连接件结合面的压力分布数据，但是结合面间加入压电薄膜破坏了实际结合面，对结合面实际接触情况影响较大。张学良等[9-11]基于接触分形理论提出了一种描述两个粗糙表面接触配对的切向、法向刚度及阻尼模型，通过仿真揭示了各相关参数对其的影响规律。一些学者也采用试验的方法研究螺栓结合部的特性，文献[12-13]利用非接触式超声波反射技术，定量分析了螺栓结合面的接触刚度与压力的分布规律，确定了不同力矩下结合面的压力分布；Campaá等[14]采用理论计算和计算机模拟的方法，计算了各向同性材料表面的法向刚度与横向刚度和泊松比的关系，并用超声波试验验证了预测；Medina等[15]提出了基于GW理论的分析模型，并预测了切向刚度成正比法向载荷和弹性模量。国内外学者多以赫兹理论或改良赫兹接触理论为基础建立统计学模型和分形模型，将粗糙表面假设为由轴对称形状且高度分布符合某种函数分布微凸体组成，且这种假设的研究对象是微小平面，这与实际结合表面的形貌存在较大差异。与上述理论相比，对不同材料、加工方式、介质等的结合部配对构件表面组成方式经过大量的试验得到的结合部基础特性参数来反映接触表面层变形的方法，更能反映结合面的真实特性。

为获取载荷作用下的螺栓结合部的静特性，用解析的方法研究在切向载荷的作用下螺栓结合部的静特性，本文基于结合部基础特性参数，建立了螺栓结合部解析的数学模型，解析模型的非线性方程组的快速准确求解是将螺栓结合部研究成果应用于工程实践的关键，在编写程序求解的同时提出了一种解析算法，实现了结合部力平衡非线性隐含积分方程组的快速准确求解，并通过加载试验验证了解析结果。

1　切向载荷下螺栓结合面数学模型

螺栓结合部数学模型是基于简单结合状态单平面结合部的解析模型建立的，建立图1所示的坐标系，X1、X2、X3表示结合部的线位移方向，X4、X5、X6表示角位移方向。螺栓结合部由螺纹结合部A、平面结合部B和平面结合部C组成，结合面上的每个等效结合点都可以用3个自由度来表示。

图1　螺栓结合部坐标系

结合部等效弹簧和阻尼特性是非线性的，可以用接触表面层的基础特性描述。结合面特性按影响因素的特征分为两大类：一类为与结构特性有关的因素，如结合面形状、类型、尺寸、散热边界条件及环境因素等，受互相连接的两构件的结构特性及尺寸形状的影响；另一类为结合面固有特性因素，包括结合面的材质及材质配对、加工方法及加工方法配对、表面粗糙度、纹理及配对、结合面间的介质等。结合面固有特性与结合面结构形状无关，两构件配对结合表面一旦确定下来，其材质、加工方法、表面粗糙度、纹理及结合面间的介质等，称为结合面基础特性。可以通过试验获得结合面单位面积的刚度和阻尼特性数据来描述结合面单位面积的法向特性和切向特性[16]，本文基于结合面基础特性参数求解外载荷下螺栓结合面上等效点的相对位移。

当螺栓受到外载荷作用时，将外载荷向坐标原点O等效，得到外载荷列阵F，外载荷作用时，外载荷F与结合面反力达到力平衡，结合部力平衡式为

(1)

当两构件在结合部部位的刚度足够大时，构件在结合部处的变形可以忽略不计，只考虑结合面的变形。图1中结合面A和结合面C的变形产生的接触反力用影响系数a表示，结合面B的接触反力用积分形式表示，单螺栓结合部的力平衡式如下：

(2)

ΔP=aEAb(u2+u6X1-u4X3)/l

式中，pi为结合面B处沿各坐标轴方向的接触面压(i=1,2,3)；S为结合面B的面积；P为螺栓的预紧力；ΔP为外载荷引起的螺栓连接力的变化量；Xi为结合面B上接触点坐标；a为螺纹接触面变形影响系数；Ab为螺栓的截面积；l为螺栓的连接长度；E为螺栓材料的弹性模量；u1,u2,…,u6为结合面沿各坐标轴方向的相对位移。

结合面各方向的面压为

(3)

(4)

式中，λi为结合面B处沿各坐标轴方向的接触变形(i=1，2，3)；φ(λ2)为方向判别参数；ατ、βτ为结合面切向的基础特性数据；αn、βn为结合面法向的基础特性数据。

结合面处沿各坐标轴方向的接触变形为

(5)

式中，λpi为结合面B处沿各坐标轴方向的预变形(i=1,2,3)。

将式(3)、式(5)代入式(2)得到外载荷作用下求解螺栓结合面相对位移的非线性积分方程组，数学模型中各载荷之间存在耦合关系，位移量u1,u2,…,u6隐含在非线性方程组中，无法直接从方程组中分离出来，为了求解位移并考虑各载荷间的耦合关系，采用弦截法编写程序迭代来求解各个方向的位移值，程序复杂且其解析精度受迭代收敛精度影响；对于单螺栓结合部仅受切向载荷的情况，本文提出了一种分步等效直接求解的方法。

2　分步载荷等效求解切向载荷作用下单螺栓结合部位移

以在预紧条件下螺栓结合部环形结合面(图2)承受切向载荷(剪切载荷F1及扭转载荷F5)的单螺栓结合部为例，设结合面法向面压均布，结合部单元受载后产生预紧载荷P引起的法向预变形λp2、切向载荷产生沿X1方向的线位移u1与沿X5方向的角位移u5。

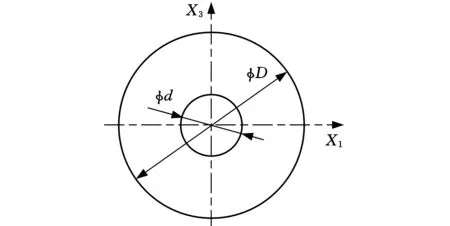
图2　螺栓结合部环形结合面

由F2=F3=F4=F6=0得u2=u3=u4=u6=0，设λp1=λp3=0，由式(5)得

(6)

由式(2)、式(3)得

(7)

(8)

由式(2)、式(3)和式(6)得

(9)

(10)

采用分步计算的方法得到单螺栓结合单元在预紧状态下施加切向载荷时结合面各方向的位移λp2、u3、u5；选用上下试件材料为调质后的45钢，环形结合面直径D=40 mm、d=13 mm，结合表面为磨削加工，表面粗糙度Ra为0.8μm，表面之间在无润滑的结合状态下。当预紧载荷为7500N，单螺栓结合部承受剪切载荷从0增大到750N时，采用程序迭代求解非线性积分方程组和采用分步载荷等效求解的计算结果的载荷-位移对比曲线如图3所示。

采用分步载荷等效求解时未考虑载荷之间的耦合关系，求解非线性隐式方程组考虑载荷间的耦合关系，比较切向载荷作用下两种算法的算例结果，计算结果误差很小；预紧力作用下，施加的切向力不超过结合面间的最大静摩擦力时，切向载荷不会引起螺栓连接力的变化，螺栓不产生变形，载荷之间的耦合影响很小。采用变量轮换弦截法编写的计算程序复杂，初值对结果影响较大，程序求解过程中还会出现迭代不收敛的现象；分步计算求解位移的方程简单，可以直接求解，在工程计算中更容易实现。

(a)剪切载荷-切向线位移曲线

(b)扭转载荷-角位移曲线图3　两种算例结果比较

两种计算结果均表明，在法向面压一定的情况下，在切向载荷作用下，载荷-位移接近正比例变化，这个结果与早期研究学者Ito等[17]的试验结果一致，间接证明了基于结合部基础特性参数建立解析模型方法的正确性。

3　承受切向载荷的单螺栓结合部试验验证及算例比较

3.1试验方案及装置设计

早期研究者通过试验研究结合部特性，但传感器精度较低，环境等因素也对试验结果的准确性有较大影响。在早期学者们对结合面特性进行试验研究[18]的基础上，本文设计了单螺栓结合面切向加载试验装置。在对螺栓结合面施加预紧载荷的同时，进行切向载荷的施加，切向载荷施载点位置不同，分别进行螺栓结合部剪切载荷和扭转载荷试验。

试验装置结构如图4所示，它由支承方箱、立柱、预紧组件和切向加载组件组成。为保证加载过程中试件和加载装置的准确的位置关系，铸造的方箱和立柱应具有足够的刚度。加载组件由施加预紧载荷的预紧组件和施加切向载荷的切向加载组件构成，加载组件、方箱、立柱等可用于不同直径的螺栓加载试验，预紧组件与螺栓直径是一一对应的，欲使螺栓直径发生变化，只需改变预紧组件中一些零件的尺寸。切向载荷经过施载钢球传递到上试件的承载面，装置的结构和安装位置保证了施加的切向载荷在上下试件的结合平面内。

(a)试验装置装配示意图

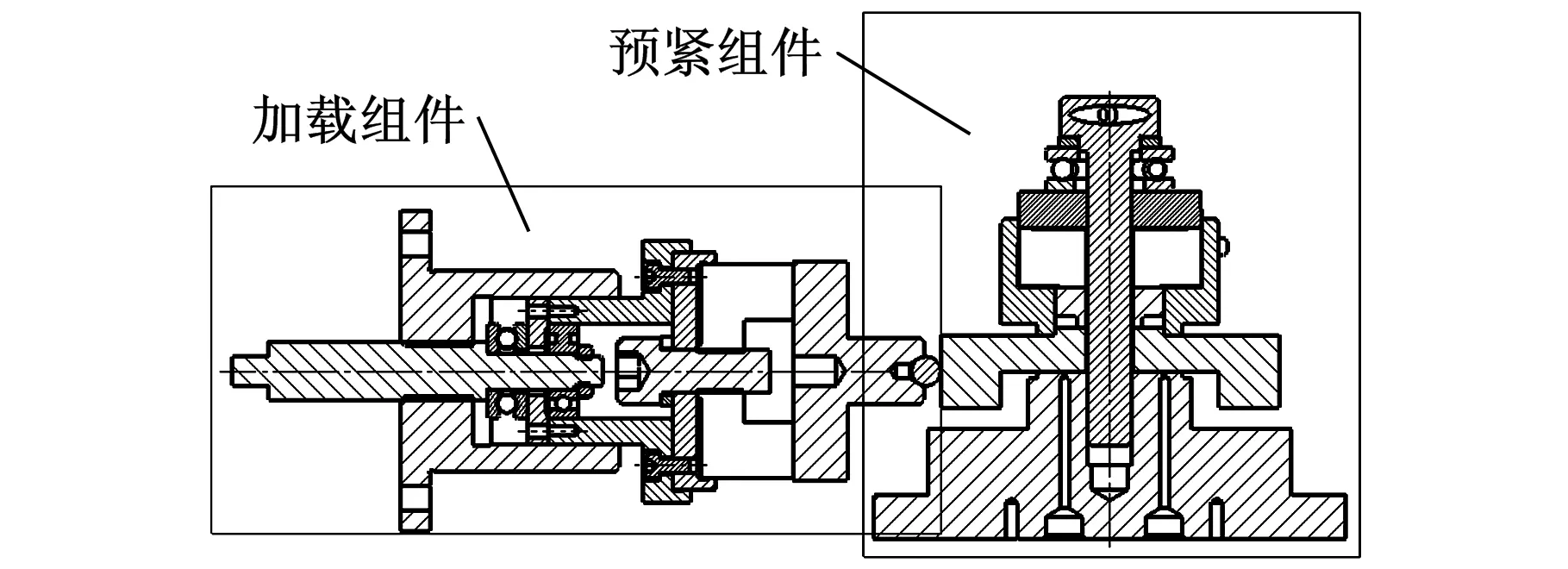
(b)试验装置预紧、加载组件图4　切向载荷施加试验装置

试验装置检测原理图如图5所示。上下试件接触面外径为40mm，表面粗糙度为0.8μm；预紧载荷通过拧紧图4预紧组件中的M12螺钉施加，其大小由FUTEK单向力传感器LTH350检测，考虑实际工作中预紧力的施加情况，试验中预紧力按螺栓能承受的最大预紧力的70%施加；切向载荷的施加由图4中的加载组件施加，切向载荷大小检测选用TR3D-A-3K三向力传感器；位移值检测选用分辨率为25nm的米铱电涡流位移传感器，力传感器和位移传感器的信号经过电荷放大后由DEWEsoft多通道数据采集仪监测采集，再传递给PC机进行数据处理。

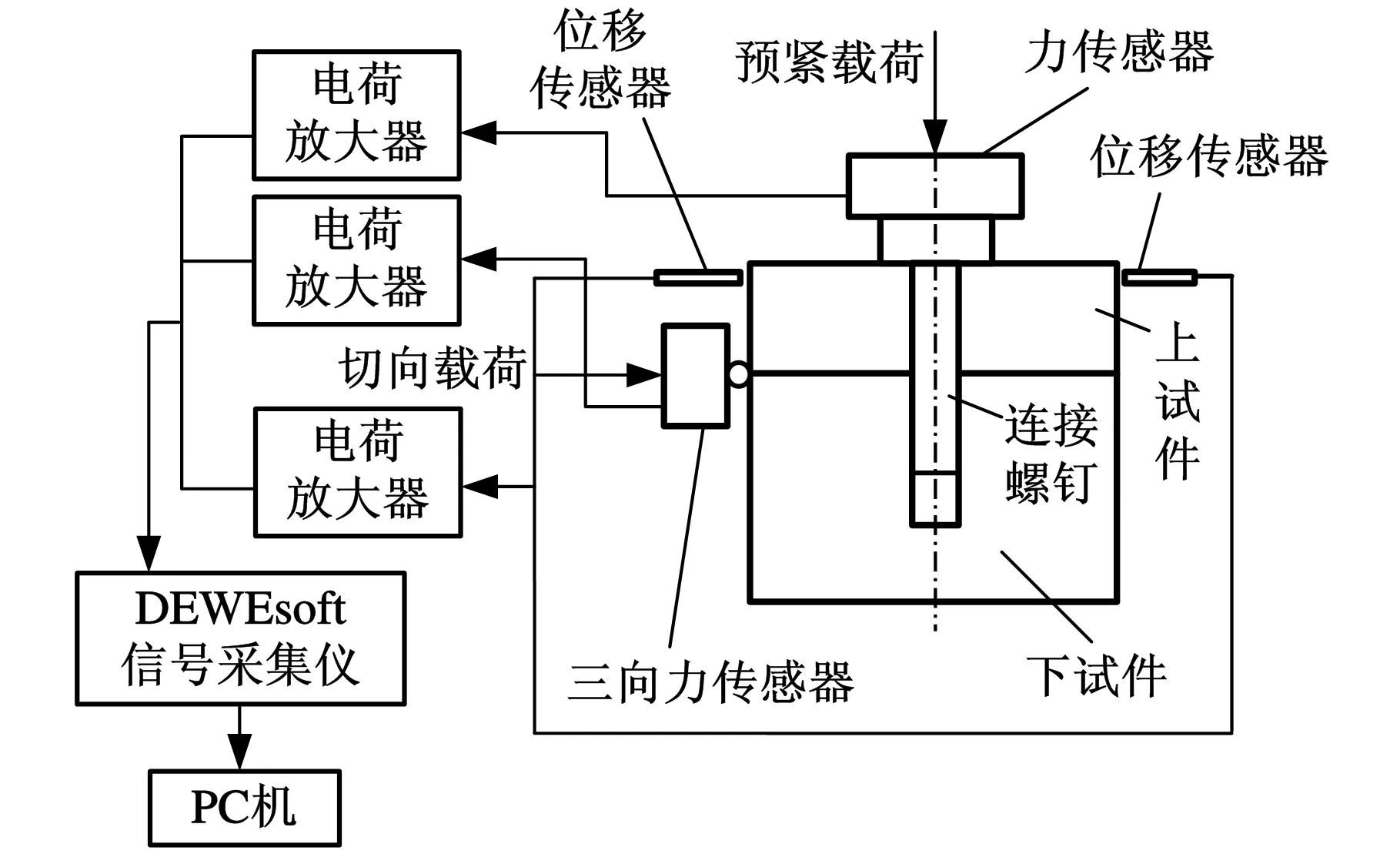
图5　加载试验原理图

图6所示为单螺栓结合部切向加载试验。对螺栓结合部单元进行切向加载试验时，上下试件的设计使其刚度尽可能高，但切向载荷的作用使得上下试件仍会产生微小的变形。为了获得螺栓结合面切向位移的准确值，试验中多次改变位移传感器测量位置，对分别位于上下试件上不同位置、不同方向的测点设置了多个位移传感器。

图6　螺栓结合部切向载荷试验

3.2承受剪切载荷的单螺栓结合部单元

切向加载试验改变切向载荷的施加加载位置(即改变扭转载荷F5)，分别进行了仅承受剪切载荷和承受扭转载荷的试验。承受剪切载荷时，切向载荷作用于上下试件结合平面内，并通过加载结合面坐标系的轴线，使得结合面仅承受剪切载荷F1，而扭转载荷F5=0。在一定预紧力作用下，施加的切向力不超过结合面间的最大静摩擦力。对多个测点的位移传感器数据进行分析得知，在切向载荷作用下，结合部会发生微滑移，且试件也会发生微小变形，获取结合部相对位移的数据处理过程要忽略微滑移和试件变形的影响。重复试验的次数越多，试件切向变形就越小，这是由于结合表面接触峰点的弹塑性变形引起的。

图7所示为在预紧载荷为7500N时，对单螺栓结合部施加的剪切载荷从0增大到750N，得到的剪切载荷F1与结合面切向变形试验结果与解析计算值的对比曲线。

图7　剪切载荷-位移比较曲线

3.3承受剪切载荷及扭转载荷的单螺栓结合部单元

改变切向载荷施加位置，使切向载荷作用于上下试件结合平面内，与结合面坐标系轴线存在偏距，产生扭转力矩，螺栓结合部呈现受剪切载荷F1和扭转载荷F5的状态。同样在预紧载荷为7500N时，单螺栓结合部施加切向载荷从0增大到750N时，得到图8所示的在切向载荷有偏距时剪切载荷F1与切向线位移u1的试验值与程序计算值的对比曲线。图9所示为在切向载荷有偏距时扭转载荷F5与切向角位移u5的试验值与程序计算值的对比曲线。

图8　剪切-扭转载荷下单螺栓结合部切向线位移

图9　剪切-扭转载荷下单螺栓结合部切向角位移

由图7～图9可知，单螺栓结合部在承受剪切载荷时，结合部切向位移与切向载荷成线性关系，由于施加切向载荷过程中，法向预紧载荷和结合面积不再改变，法向面压值一定；在一定的试验条件下，结合表面的材料、加工方式、介质等不变，结合面基础特性不变，切向变形与切向载荷呈线性变化。由试验曲线分析得知，结合面的切向加载和卸载的位移变形过程出现迟滞现象，是由于结合表面的微凸体峰点的弹塑性变形和弹性变形恢复滞后引起的。

将试验值和计算值曲线进行对比，发现试验值和计算值变化趋势一致，但存在一定的误差，这是因为试验中位移传感器精度高，外界微小的干扰信号就会对传感器的读数产生影响，尽管位移传感器信号波动被控制在0.05μm以内，但当载荷较小时，测量值也很小，传感器的精度误差对测量结果影响的比例较大，随着切向载荷的增大，误差的影响减小，切向载荷大于200N后，计算结果和测量结果误差在10%以内。

对单螺栓结合部在承受剪切载荷和扭转载荷时的载荷-位移曲线进行分析，不论是切向线位移还是切向角位移，计算结果与试验结果的一致性证明了本文基于结合面基础特性建立的单螺栓结合部解析模型是正确的，本解析模型可以表征结合面特性，也可以用于单螺栓结合部特性分析。

4　结论

(1)本文基于结合面基础特性参数建立了螺栓单元结合面的解析模型，提出了分步载荷等效求解切向载荷下螺栓结合面的静特性方法，并进行了解析和试验验证，证明了本解析模型和方法的正确性。

(2)在一定预紧力作用和切向力不超过最大静摩擦力的情况下，切向变形与外载荷成线性关系；切向载荷作用下结合部会发生微滑；重复受压使结合表面的接触峰点发生弹塑性变形和塑性变形，试件切向变形值减小。

(3)结合面基础特性参数与结合面的结构无关，具有通用性。本文提出的基于结合面基础特性参数求解切向载荷下螺栓结合面位移的方法具有通用性，可适用于不同结构形式和不同规格的螺栓结合面解析，以便机床等前期设计时预测结合部静态刚度。

[1]田红亮，刘芙蓉，方子帆，等.结合部静摩擦因数修正与定量实验验证[J].农业机械学报，2013，44(10)：282-292.

TianHongliang，LiuFurong，FangZifan，etal.CorrectionofStaticFrictionCoefficientforJointInterfaceandQuantitativeTestConfirmation[J].TransactionsoftheChineseSocietyforAgriculturalMachinery，2013，44(10)：282-292.

[2]赵宏林，丁庆新，曾鸣. 机床结合部特性的理论解析及应用[J]. 机械工程学报，2008，44(12)：208-214.

ZhaoHonglin，DingQingxin，ZengMing，etal.TheoreticAnalysisonandApplicationofBehaviorsofMachineToolJoints[J].JournalofMechanicalEngineering，2008，44(12)：208-214.

[3]LinY，ChenW.AMethodofIdentifyingInterfaceCharacteristicforMachineToolsDesign[J].JournalofSoundandVibration，2002，255：481-487.

[4]FuWeiping，HuangYumei，ZhangXueliang，etal.ExperimentalInvestigationofDynamicNormalCharacteristicsofMachinedJointSurfaces[J].ASMEJournalofVibrationandAcoustics，2000，122(4)：393-398.

[5]田红亮，钟先友，秦红玲，等. 依据各向异性分形几何理论的固定结合部法向接触力学模型[J].机械工程学报，2013，49(21)：108-121.

TianHongliang，ZhongXianyou，QinHongling，etal.NormalContactMechanicsModelofFixedJointInterfaceAdoptingAnisotropicFractalGeometricalTheory[J].JournalofMechanicalEngineering，2013，49(21)：108-121.

[6]MengAD.OpticalControlofFastenerClampLoadinBoltJoints[D].Rochester：OaklandUniversity, 2008.

[7]黄玉美,惠烨,杨新刚，等.螺栓结合面单元全载荷静特性试验装置及试验方法:中国,ZL201010236266.8[P]. 2010-11-17.

[8]杨国庆，王飞，洪军，等. 螺栓连接被连接件刚度理论计算方法研究[J].西安交通大学学报，2012，46(7)：50-56.

YangGuoqing，WangFei,HongJun，etal.TheoreticalAnalysisforBoltedMemberStiffness[J].JournalofXi’anJiaotongUniversity，2012，46(7)：50-56.

[9]张学良，黄玉美，韩颖.基于接触分形理论的机械结合面法向接触刚度模型[J].中国机械工程，2000，11(7)：727-729.

ZhangXueliang，HuangYumei，HanYing.FractalModeloftheNormalContactStiffnessofMachineJointsurfacesBasedontheFractalContactTheory[J].ChinaMechanicalEngineering，2000，11(7)：727-729.

[10]张学良，黄玉美，温淑华.结合面接触刚度分形模型研究[J].农业机械学报，2000，31(4)：89-91.

ZhangXueliang，HuangYumei，WenShuhua.FractalModelofContactStiffnessofJointSurfaces[J].TransactionsoftheChineseSocietyforAgriculturalMachinery，2000，31(4)：89-91.

[11]张学良，丁红钦，兰国生.基于分形理论的结合面法向接触阻尼与损耗因子模型[J].农业机械学报，2013，44(6)：288-294.

ZhangXueliang,DingHongqin,LanGuosheng,etal.NormalContactDampingandDissipationFactorModelofJointInterfacesBasedonFractalTheory[J].TransactionsoftheChineseSocietyforAgriculturalMachinery，2013，44(6)：288-294.

[12]PauM,BaldiA,LebanB.VisualizationofContactAreasinBoltedJointsUsingUltrasonicWave[J].ExperimentalTechniques，2008，32(4)：49-53.

[13]MarshallMB,LewisR,Dwyer-JoyceRS.CharacterizationofContactPressureDistributioninBoltedJoints[J].Strain，2006，42：31-43.

[14]MedinaS，NowellD,DiniD.AnalyticalandNumericalModelsforTangentialStiffnessofRoughElasticContacts[J].TribologyLettersJanuary，2013, 49(1)：103-115.

[15]CampaáC,PerssonBN,MüserMH.TransverseandNormalInterfacialStiffnessofSolidswithRandomlyRoughSurfaces[J].JournalofPhysics:CondensedMatter，2011，23(8)：085001.

[16]ZhangGuangpeng，HuangYumei，ShiWenhao，etal.PredictingDynamicBehaviorofaWholeMachineToolStructureBasedonComputer-aidedEngineering[J].InternationalJournalofMachineToolsandManufacture，2003，43：699-706.

[17]ItoY,MasukoM.ExperimentalStudyontheOptimumInterfacePressureonaBoltedJointConsideringtheDampingCapacity[C]//Proceedingsofthe12thInternationalConferenceonMachineToolDesignandResearch.Birmingham，1972:97-105.

[18]SherifHA,KossaSS.RelationshipbetweenNormalandTangentialContactStiffnessofNominallyFlatSurfaces[J].Wear,1991，151(1)：49-62.

(编辑陈勇)

Theoretical Analysis and Test on Static Characteristics of Bolt Joints under Tangential Load

Hui Ye1,2Huang Yumei1Li Yan1

1.Key Laboratory of NC Machine Tools and Manufacture Equipment Integrated of the Educational Ministry,Xi’an University of Technology,Xi’an,710048 2.Shaanxi University of Science&Technology,Xi’an,710021

To observe the static performance of bolt joints accurately, an analytic mathematical model of bolt unit interfacing was established based on joint interfaces basic characteristic parameters. A multi-stage equivalent load analyzing algorithm was proposed to solve non-linear implicit integration equations quickly and correctly when tangential load was applied to the joints, not considering the coupling relation among loads. Torsional and tangent loading tests were conducted using self-designed bolt joint tangent loading device. The results of the tests and analyses indicate that when tangential load does not exceed the maximum static friction, the results reveal a linear relation between joint interface tangential deformation and external load. The consistence between the analysis and test results validates the correctness of analytic model, which provides theoretical and test evidence for investigating static performance of mechanical interface, and the analyzing algorithm makes it easy to apply the joint interface research fruits to engineering practice.

bolt joint；static characteristic；tangential load；multi-stage algorithm

2014-10-17

国家高技术研究发展计划(863计划)资助项目(2012AA040701)；陕西省自然科学基金资助项目(2013JM7014,2014JM7275)

TG50< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.07.007

惠烨，女，1972年生。西安理工大学机械与精密仪器学院博士研究生，陕西科技大学机电工程学院副教授。主要研究方向为机械结合部及数控机床检测技术。黄玉美，女，1941年生。西安理工大学机械与精密仪器学院教授、博士研究生导师。李艳，女，1970年生。西安理工大学机械与精密仪器学院副教授、博士。