2(2-UPR+SPR)串并联机构雅可比矩阵的建立

胡　波　宋春晓　张庆玲　于晶晶

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.燕山大学先进锻压成型技术与科学教育部重点实验室，秦皇岛，066004

2(2-UPR+SPR)串并联机构雅可比矩阵的建立

胡波1,2宋春晓1,2张庆玲1,2于晶晶1,2

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.燕山大学先进锻压成型技术与科学教育部重点实验室，秦皇岛，066004

建立了一种新型串并联机构的雅可比矩阵。首先，介绍了一种新型的2(2-UPR+SPR)串并联机构，该机构由两个2-UPR+SPR机构串联而成，它具有串联机构和并联机构的共同优点。然后，根据2-UPR+SPR机构中存在的几何约束建立了其速度约束矩阵和速度耦合矩阵。最后，分析了2(2-UPR+SPR)串并联机构的速度传递关系，通过合理处理独立并联机构的速度耦合和约束关系，建立了2(2-UPR+SPR)串并联机构整体正向和逆向雅可比矩阵。研究结果表明，2(2-UPR+SPR)机构的雅可比矩阵包含各个独立并联机构的运动、约束和耦合信息。所提出的建立2(2-UPR+SPR)机构雅可比矩阵的方法也适合其他串并联机构。

串并联机构；Exechon机构；雅可比矩阵；运动学

0　引言

近年来，由并联机构串联而成的串并联机构引起了国内外学者的关注[1-6]。这类机构是由两个或多个并联机构串联而成的，具有串联机构和并联机构的共同优点，有着良好的应用前景。在该领域，Tanev[2]提出了一种串并联机构，该机构的运动可由机构中一串联支链确定，借助该串联支链将机构的运动学问题转变为串联机器人的运动学问题来进行分析。Zheng等[3]提出了一种可作为海洋采矿补偿平台的上下层分别为3-UPU平动机构、3-UPU转动机构的串并联机构。Hanan等[4]采用以并联构型为单元的串并联机构研制了仿生机械象鼻。Lu等[5]研究了以3-SPR机构为单元的串并联机构基本运动学模型。Gallardo等[6]采用螺旋理论研究了由3-RPS机构构成的串并联机构的运动学和动力学问题。串并联机构属于有别于传统串联机构和并联机构的一类机构，相比之下，串联机构和并联机构的理论研究相对成熟，基本理论体系已经形成，而串并联机构机型相对缺乏，且基础理论极不成熟，严重阻碍了这类机构的广泛应用。本文提出了一种新型的2(2-UPR+SPR)串并联机构，该机构由2个2-UPR+SPR并联机构串联而成。2-UPR-SPR并联机构因其结构简单、运动性能好的特点而被用作Exechon五轴混联加工中心的定位模块，该机构近年来也引起了学术界的广泛重视[7-8]。采用2个2-UPR+SPR机构构成串并联机构可以获得高转动能力和大工作空间，2(2-UPR+SPR)机构是一种具有一定实用价值的串并联机构。

众所周知，雅可比矩阵在研究机构的运动学、奇异特性、性能指标等方面有着重要的作用，针对并联机构的雅可比矩阵，国内外学者进行了大量的研究工作[9-12]，包括少自由度并联机构n×n型雅可比矩阵[9]、6×6型雅可比矩阵[10-11]、用于性能分析的统一量纲雅可比矩阵[12]等。而针对串并联机构的雅可比矩阵研究尚未见报道。传统的串并联机构速度求解仅将2个独立并联机构速度叠加，并未建立这类机构的整体正向和反向雅可比矩阵，因此无法对这类机构进行深层次的理论研究。实际上，约束和耦合是少自由度并联机构的本质特点，正确地应用这一特性是建立这类串并联机构雅可比矩阵的关键。然而以往的研究没有把这些因素综合考虑，因而未建立起这类机构的整体雅可比矩阵。基于此，本文以2(2-UPR+SPR)型串并联机构为研究对象，建立该机构的整体雅可比矩阵。

1　2(2-UPR+SPR)机构描述

图1为2(2-UPR+SPR)串并联机构的机构简图。2(2-UPR+SPR)机构由2个2-UPR+SPR机构串联而成。其中，位于底部的2-UPR+SPR机构称为机构1，位于上部的2-UPR+SPR机构称为机构2。独立并联机构i(i=1,2)包括一个下平台Ai和一个上平台Bi。Ai、Bi分别为等边三角形，其中，Aij、Bij(i=1,2; j=1, 2, 3) 分别为上下平台各端点。则A1可视为整个串并联机构的基座，B2可视为整个串并联机构的运动平台。独立并联机构2的下平台A2和独立并联机构1的上平台B1固联，且尺寸相同。B1可由A2逆时针旋转θ角得到。

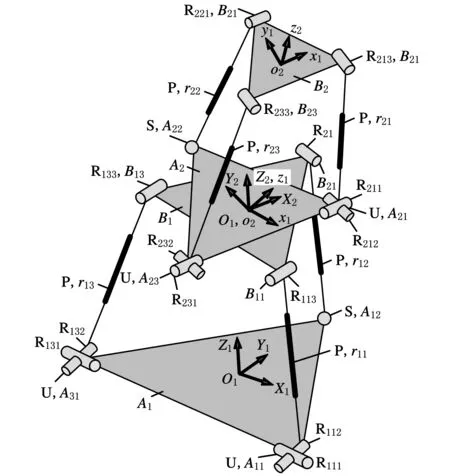
图1　2(2-UPR+SPR)机构简图

在第i个2-UPR+SPR机构中，上下平台各端点Aij、Bij通过3个分支rij(i=1,2; j=1,2,3)连接，机构的1、3分支中，Aij和Bij分别通过2个相同的UPR分支连接，其中，U副由2个相互正交的R副组成，在第2个分支中，Ai2和Bi2通过一个SPR分支连接(图1)。第i个独立并联机构中第j个分支自下而上的第k个R副分别记为Rijk(i=1,2; j=1, 2, 3, k=1, 2, 3)。定义：⊥表示垂直符号，∥表示平行符号。则机构i的第1、3分支中运动副存在以下几何关系：

(1)

i=1, 2j=1,3

机构i的第2分支中存在以下几何关系：

ri2⊥Ri21Ri21∥Bi1Bi3

(2)

2(2-UPR+SPR)机构中，总的构件数目n=15，包括1个静平台A1、1个动平台B2、1个中间平台A2/B1，6个摆动分支，6个伸缩分支。运动副数目g =18，包括6个转动副R、6个移动副P、4个万向副U和2个球副S。各2-UPR+SPR机构中有2个过约束[8]，整个2(2-UPR+SPR)串并联机构的过约束数目u=4。机构局部自由度数为0，则这类串并联机构的自由度为

(3)

式中，ki为第i个运动副的自由度数。

如图1所示，以机构i下平台中心Oi(i=1,2)为原点建立坐标系Ai，坐标轴分别为Xi、Yi、Zi(Xi∥Ai1Aij3, YiAij1Aij3, ZijAi)。以机构i上平台中心oi为原点建立坐标系Bi，坐标轴分别为xi、yi、zi(xi∥Bi1Bij3, yiBij1Bij3, ziBi)。设机构各点Q在坐标系N中表示为NQ, 其中Q可取Aij，Bij，Oi，oi(i=1,2；j=1,2,3),N可取Ai,Bi。设坐标系K(K可取Ai,Bi)相对于N的旋转变换矩阵为点Q在坐标系N中的线速度矢量，表示坐标系K相对于坐标系N的角速度矢量。

就各2-UPR+SPR机构而言，下平台端点Aij(i=1, 2;j=1, 2, 3)在各自坐标系Ai中可表示为

(4)

式中，Ei为平台Ai中心到各端点的距离。

各2-UPR+SPR机构上平台端点Bij(i=1,2;j=1,2,3)在各自坐标系Bi中可表示为

(5)

式中，ei为平台Bi中心到各端点的距离。

端点Bij(i=1,2;j=1,2,3)在坐标系Ai中可表示为

(6)

2　机构的运动耦合和约束分析

2.12-UPR+SPR机构速度耦合分析

由2-UPR+SPR机构中各转动副的方位，可得各R副在其下平台坐标系Ai的单位矢量：

(7)

由式(1)、 式(2)，可得

(8)

由式(4)～式(8)可得

yli=0

(9)

Xoi=(3Eixmiymi-eixmi+2Zoizli)/(2xliymi)

(10)

Yoi=(ei-Eiymi-2Zoiyni)/(2ymi)

(11)

采用XZY欧拉角来表示2-UPR+SPR机构中坐标系Bi相对于坐标系Ai的旋转,即动坐标系Bi先与静坐标系Ai重合，然后绕Xi轴旋转αi角，再绕新的zi轴旋转βi，最后绕新的yi轴旋转λi角得到。为表达方便，本文中规定sinΦ=sΦ，cosΦ=cΦ，其中Φ=αi，βi，λi。则机构的旋转矩阵可表示为

(12)

由yli=0，可得

βi=0

(13)

旋转矩阵进一步简化为

(14)

由式(10)、式(11)和式(14)，Xoi、Yoi可表示为

Xoi=tanλi(3Eisαi/2-eitanαi/2+Zoi/cαi)

(15)

Yoi=ei/(2cαi)-Ei/2-Zoitanαi

(16)

式(15)、式(16)表明，2-UPR+SPR机构上平台的位置Xoi、Yoi、Zoi并不独立，它们之间存在耦合关系。Xoi、Yoi、Zoi是关于其广义坐标αi、λi、Zoi的函数。结合式(15)、式(16)，上平台Bi中心相对于其下平台Ai的线速度可表示为

(17)

式(17)中各元素可由Xoi、Yoi、Zoi求偏导得到：

2-UPR+SPR机构的上平台Bi相对于其下平台Ai的角速度可表示为欧拉角速度的叠加：

(18)

式中，Rα i、Rλ i分别为欧拉角αi、λi的转轴对应的单位矢量。

由式(17)、式(18)可得

(19)

式(19)为2-UPR+SPR机构的速度解耦方程，表示2-UPR+SPR机构的末端6维速度和其广义坐标速度间的映射关系，Joi为该机构的速度解耦矩阵。

2.22-UPR+SPR机构速度约束分析

2-UPR+SPR机构各分支中存在着约束力/力矩，这些约束力矩对机构末端速度有约束作用。根据确定约束力/力矩的几何法[11]，可知在UPR分支中存在一过U副中心且与Ri3平行的约束力，并存在一垂直于分支中所有R副的约束矩。在SPR分支中存在一过球副S中心且平行于该分支中R副的约束力。即2-UPR+SPR机构中含3个约束力和2个约束矩。设第i个2-UPR+SPR机构第j个分支中存在的约束力的方向矢量为fij(i=1,2;j=1,2,3)，约束矩方向矢量为τij(i=1,2;j=1,3)。由约束力/力矩的性质可得

(20)

(21)

dij=Aij-oifi1=fi3=yifi2=xi

τi1=τi3=Ri11×Ri12=Ri31×Ri32

式(20)、式(21)写成矩阵形式如下：

(22)

记式(22)第j行为Jsij, 可得

(Jsi3-Jsi1)/(aEi)=Jsi4

(23)

Jsi4=Jsi5

(24)

可见Jsi中线性无关项只有3项，独立2-UPR+SPR机构存在2个冗余约束。

从式(22)中取出前3项线性无关项，构成以下速度约束矩阵：

(25)

式(25)为2-UPR+SPR机构的速度约束方程，它体现了机构的速度约束特性，表明机构的6维速度是在该式约束下的速度。Jvi为该机构的速度约束矩阵。

3　2(2-UPR+SPR)整体雅可比矩阵的建立

2-UPR+SPR机构是由3个线性分支组成的机构，对应这类机构的分支速度与动平台末端6维速度之间的关系可表示为[1,11]

(26)

式中，vrij(i=1,2;j=1,2,3)为分支rij的速度；Jαi为第i个机构的驱动速度矩阵。

设t为一任意3维向量，t=[txtytz]T，G(t)满足

(27)

对于2(2-UPR+SPR)机构中的旋转变换矩阵，存在以下关系：

(28)

(29)

(30)

2(2-UPR+SPR)机构末端平台中心o2在基坐标系A1中可表示为

(31)

式(31)对时间求导可得：

(32)

2(2-UPR+SPR)机构末端平台B2相对于基坐标系A1的角速度为

(33)

由式(32)、式(33)可知，2(2-UPR+SPR)机构末端平台B2相对于基坐标系A1的速度为

(34)

式中，E3×3为3×3单位矩阵。

由式(19)、式(25)可得

(35)

由式(34)、式(35)可得

(36)

式中，JF为2(2-UPR+SPR)机构的正向雅可比矩阵。

(37)

式(37)两端同左乘Jv1并结合式(25)可得

(38)

由式(19)、式(38)，可得

(39)

由式(19)、式(38)和式(39)，可得

(40)

同理可得

(41)

由式(40)和式(41)，可得

(42)

式中，JI为2(2-UPR+SPR)机构的反向雅可比矩阵。

4　算例

设定机构的尺寸参数为E1=120 cm,E2=e1=80 cm,e2=60 cm,机构1上平台位姿参数设定为(α1=-10°,λ1=8°,Zo1=115 cm),机构2上平台位姿参数设定为(α2=-10°,λ2=8°,Zo2=115 cm)。

根据理论模型，计算可得此位形下机构1和机构2的驱动速度矩阵：

Jα1=

机构1和机构2的速度耦合矩阵分别为

机构1和机构2的速度约束矩阵分别为

2(2-UPR+SPR)机构的雅可比矩阵为

给定vr1=[1 23]Tcm/s,vr2=[456]Tcm/s，计算可得机构末端速度：

A1vo2=[6.11054.40185.2358]cm/s

5　结论

(1)本文通过分析2-UPR+SPR机构中的几何约束，建立了2-UPR+SPR机构的速度约束矩阵和速度解耦矩阵，揭示了该机构末端速度约束和耦合的特性。这两个矩阵在2(2-UPR+SPR)机构整体雅可比矩阵建立过程中起到了重要作用。

(2)机构末端运动的约束和耦合是少自由度并联机构的本质特点，这些特点在串并联机构中必然有所体现。通过融合2-UPR+SPR的约束和耦合信息，得到了2(2-UPR+SPR)机构的整体雅可比矩阵。研究结果表明，所得到的2(2-UPR+SPR)机构的雅可比矩阵包含了各个2-UPR+SPR并联机构的所有信息。其中，Jαi包含了机构的运动信息，Jvi包含了机构的约束信息，Joi包含了机构的耦合信息。本文方法也适合其他串并联机构。

[1]黄真，赵永生，赵铁石.高等空间机构学[M].北京：高等教育出版社，2006.

[2]Tanev T K.Kinematics of a Hybrid(Parallel-serial) Robot Manipulator[J].Mechanism and Machine Theory, 2000,35(9):1183-1196.

[3]Zheng Xiangzhou,Bin Hongzan,Luo Yougao.Kinematic Analysis of a Hybrid Serial-parallel Manipulator[J].International Journal of Advanced Manufacturing Technology,2004,23 (11/12): 925-930.

[4]Hanan M W,Walker I A.Kinematics and the Implementation of an Elephant’s Trunk Manipulator and Other Continuum Style Robots[J].J. Robot. Syst., 2003, 20(2):45-63.

[5]Lu Yi,Hu Bo,Sun T.Analyses of Velocity,Acceleration,Statics and Workspace of a 2(3-SPR) Serial-parallel Manipulator[J].Robotica,2009,27(4):529-538.

[6]Gallardo J,Aguilar C,Casique L,et al.Kinematics and Dynamics of 2(3-RPS) Manipulators by Means of Screw Theory and the Principle of Virtual Work[J].Mechanism and Machine Theory,2008,43(10):1281-1294.

[7]Bi Z M,Jin Y.Kinematic Modeling of Exechon Parallel Kinematic Machine[J].Robotics and Computer-Intergrated Munufacturing,2011,27(1):186-193.

[8]Bi Z M.Kinetostatic Modeling of Exechon Parallel Kinematic Machine for Stiffness Analysis[J].The International Journal of Advanced Manufacturing Technology,2014,71(1/4):325-335.

[9]李剑锋，费仁元，范金红，等.具有大位置空间的3自由度并联机构运动性能分析[J].机械工程学报，2007，43(8):53-59.

Li Jianfeng,Fei Renyuan,Fan Jinhong,et al.Kinematic Performance Analysis of 3-DOF Parallel Mechanism with Large Positional Workspace[J].Chinese Journal of Mechanical Engineering,2007,43(8):53-59.

[10]Joshi S,Tsai L W.Jacobian Analysis of Limited-DOF Parallel Manipulators[J].ASME Journal of Mechanical Design,2002,124(2):254-258.

[11]Lu Yi,Hu Bo.Unification and Simplification of Velocity/acceleration of Limited-dof Parallel Manipulators with Linear Active Legs[J].Mechanism and Machine Theory,2008,43(9):1112-1128.

[12]Kim S G,Ryu J.New Dimensionally Homogeneous Jacobian Matrix Formulation by Three End-effector Points for Optimal Design of Parallel Manipulators[J].IEEE Transactions on Robotics and Automation,2003,19(4): 731-736.

(编辑陈勇)

Jacobian Matrix Establishment of 2(2-UPR+SPR) Serial-parallel Manipulator

Hu Bo1,2Song Chunxiao1,2Zhang Qingling1,2Yu Jingjing1,2

1.Parallel Robot and Mechatronic System Laboratory of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of National Education,Yanshan University,Qinhuangdao,Hebei,066004

The Jocobian of a novel 2(2-UPR+SPR) serial-parallel manipulator was established.First, a 2(2-UPR+SPR) serial-parallel manipulator formed by two 2-UPR+SPR mechanisms was presented. This manipulator could provide advantages of both serial and parallel manipulators. Second, the velocity decoupling and velocity constraint equations for single 2-UPR+SPR were analyzed based on the geometric constraints in the mechanism. Finally, the velocity transfer relation for the 2(2-UPR+SPR) serial-parallel manipulator was analyzed. Based on the velocity decoupling and constraint characteristics of single 2-UPR+SPR mechanism, the integral forward and inverse Jacobian matrix for 2(2-UPR+SPR) serial-parallel manipulator were established. The results show that the established Jacobian matrices contain kinematics, coupling and constraint information of each 2-UPR+SPR mechanism. The methodology for establishing the integral Jacobian matrix of the 2(2-UPR+SPR) serial-parallel manipulator herein is also fitable for other serial-parallel manipulators.

serial-parallel manipulator; Exechon manipulator; Jacobian matrix; kinematics

2014-04-28

国家自然科学基金资助项目(51305382)；河北省高等学校科学技术研究优秀青年基金资助项目(YQ2013011)；机器人技术与系统国家重点实验室开放研究基金资助项目(SKLRS-2012-MS-01)；河北省科技计划资助项目(13211610)；燕山大学机械工程学院协同创新研究项目(JX2014-02)

TH112DOI：10.3969/j.issn.1004-132X.2015.07.001

胡波,男,1982年生。燕山大学机械工程学院副教授。主要研究方向为并联机器人。发表论文30余篇。宋春晓,女, 1990年生。燕山大学机械工程学院硕士研究生。张庆玲,女, 1980年生。燕山大学机械工程学院高级实验师。于晶晶,女, 1981年生。燕山大学机械工程学院博士研究生。