基于AMESim的特高压断路器管道系统压力波动

赖奇暐　巫世晶　张增磊　胡基才

武汉大学，武汉，430072

基于AMESim的特高压断路器管道系统压力波动

赖奇暐巫世晶张增磊胡基才

武汉大学，武汉，430072

针对特高压断路器管道系统中产生的液压冲击波对操动系统运行的影响，以蓄能器及其管道系统作为研究对象，在分析其压力波动产生机理的基础上，确立了管道子模型的选取原则，应用AMESim软件建立了液压系统的综合仿真模型，对模型进行求解后得到了液压管道的压力波动特性，同时分析了管道长度和内径对压力波动幅度的影响。研究结果表明：现有管道系统的压力波动幅度较大，不利于系统的稳定运行；对管道长度和内径组合进行优化设计后，压力波动的降幅在50%以上。所采用的研究方法对特高压断路器管道系统的优化设计具有参考价值。

管道系统；压力波动；参数优化；特高压断路器

0　引言

特高压断路器作为电力系统中最重要、最复杂的电气开关设备之一，起到控制特高压输电设备可靠、高效、安全运行的作用。特高压断路器操动机构具有传递功率大、动作速度快等特点，因此大功率特高压断路器大部分采用液压操动机构来保证其工作可靠性。在特高压断路器进行分合闸时，由于分合闸极短的额定时间会导致合闸速度高达5 m/s，分闸速度甚至高达12.5 m/s，液压操动机构系统中管路流量会突然变化，从而引发压力的剧烈变化，液压冲击波在管路中的来回传播会直接影响系统管接头的链接和密封件的保护，从而影响系统的可靠性。同时，管道油液额定压力高达32.6 MPa，若动态压力小于额定压力、蓄能器的压力减小将会导致分合闸闭锁现象，导致断路器无法正常工作。因此，需要对液压管路冲击波的产生机理、动态特性进行分析，并提出相关改进措施，从而减少甚至避免误动作的出现[1-3]。

文献[4]用节点法建立了液压回路数学模型，根据容腔节点表征回路压力变化。文献[5]采用分布参数模型的近似思想，针对钢制圆形液压管路建立集中参数的动态模型，计算管道脉冲响应与流量波动响应。文献[6]利用MATLAB Simulink中的SELCETOR模块来求解时间和空间域上的二维偏微分方程，计算管道中压力脉动动态响应特性。文献[7]利用无穷乘积法建立了管路流体流动数学模型，对管路系统进行动态特性仿真。文献[8]采用差分与特征线法编程计算的方法来研究压管道水击强度。上述文献采用不同方法对管道压力波动特性进行建模分析，仅仅针对孤立的液压管道系统，未充分考虑液压系统中其他元件对管道压力波动的影响。同时，管道的复杂程度对液压系统波动效应的影响也未能得到考虑。因此，为了更好地对管道压力波动特性进行研究，在管道压力波动数学模型的基础上需要针对不同管道的特点进行具体建模，并需要考虑系统中其他构件的综合影响。

本文以1100 kV特高压断路器液压操动机构为研究对象，在分析管道压力波动产生机理的基础上，建立了液压管道系统的AMESim综合仿真模型，并对蓄能器出口到主阀的4条管路的压力波动特性进行综合分析，最终通过管道的组合优化来减小压力波动，提高液压系统运行的可靠性。

1　管道压力波动基本方程

管道内压力波动主要由水击现象引起，是一种特殊的非恒定流。当前主流水击理论主要是基于一维非恒定的基本微分方程组，在处理后得到能解决水击问题的基本方程[9-10]。在管道中选取微小流段，如图1所示。图中，A为1-1截面的面积，m2；v为流速，m/s；ρ为液体密度，kg/m3；t为时间。假定管道为线性变形且是小变形的材料，液体的密度相对变化量较小，根据质量守恒原理，可得非定常流连续性方程：

(1)

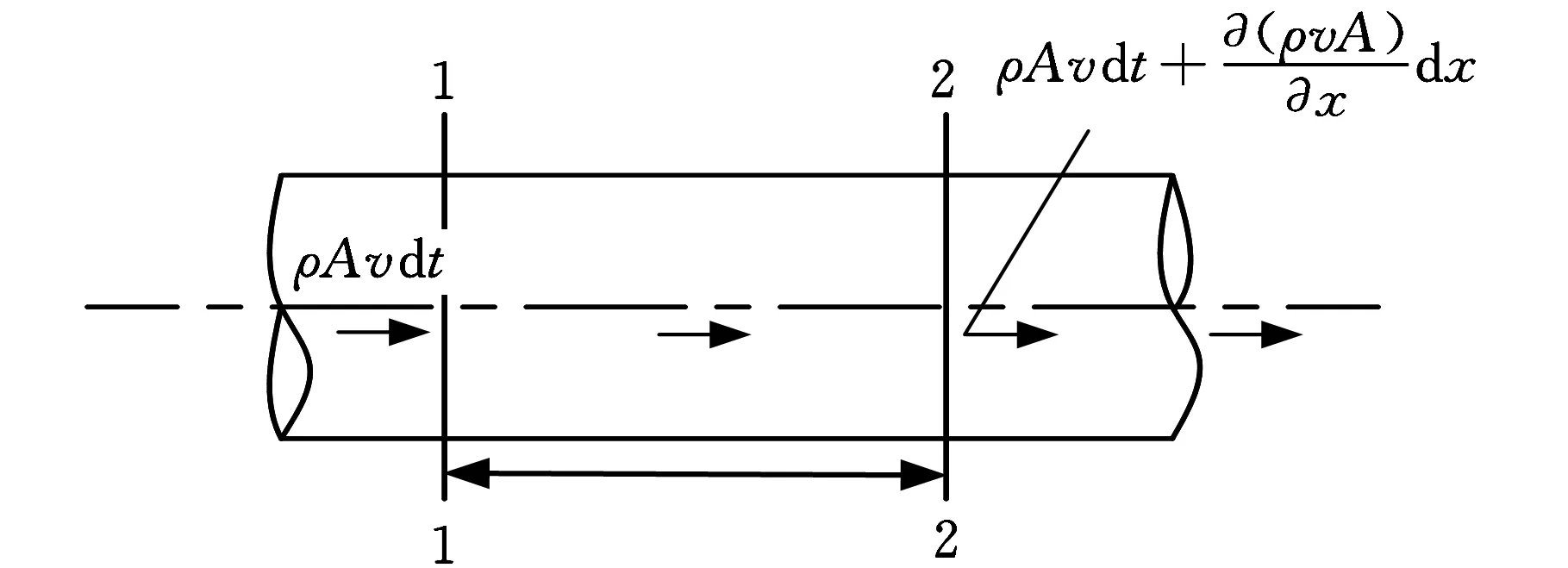
图1　水击连续性方程推导示意图

由于工程上常使用水头H，将式(1)整理并改写成用水头H表示的方程：

(2)

式中，c为波速，m/s；α为x轴与水平面的夹角。

(3)

式(2)与式(3)为管道非定常流连续性方程的使用形式，主要考虑了液体的压缩性与管壁的弹性变形。

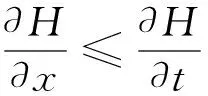
(4)

在总流中取长为dx的微小流段作为隔离体，坐标轴x的方向与液体流动方向一致，如图2所示。

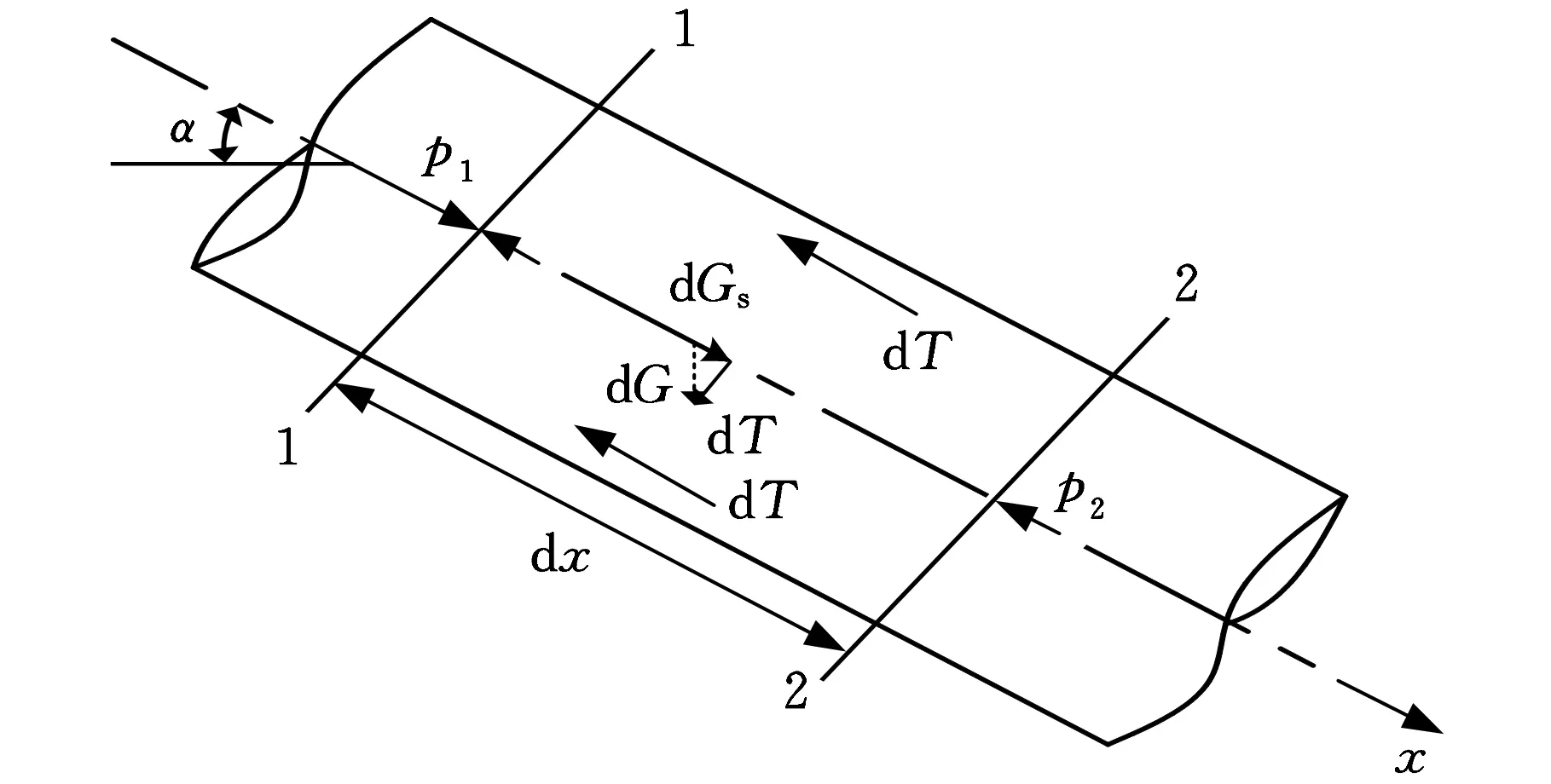
图2　水击运动方程推导示意图

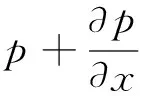
(5)

考虑压力与水头的关系，将水利坡度关系式代入式(5)，得到水击运动方程：

(6)

式中，D为管道内径，mm。

(7)

2　管道系统仿真模型

AMESim软件中根据管道长细比以及黏性系数的大小，提供了23种管道模型，主要涉及3种流体现象：Compressibility(C容性)，用于计算压力；Friction(R阻性)，用于计算沿程压力损失；Inertia(I惯性)，用于计算波动效应[11]。一般来说，管道模型越复杂，计算结果越精确。但复杂的管道模型可能与其他模型发生冲突而导致计算速度变慢甚至计算失败，因此应该根据实际结果合理选择管道模型。在AMESim的管道模型中，需要着重考虑以下3个参数：

(1)长细比Aratio=L/D。其中，L为管长，mm。该参数用来判断管路的几何特征是短粗管还是长细管[12]。

(2)波动传播时间Twave=L/a。其中，a为声速，取340 m/s。Twave通常与计算时间步长Tcount相比较，Tcount表示关心的频率范围，用比较的结果来决定是否要考虑波动效应。如果该时间小于仿真设定的通讯时间(communication interva，即所需要的采样时间)，则没有必要选择考虑波动效应的模型，Twave的计算公式为

Twave=L/c

(8)

(9)

式中，β为液体体积弹性模量，MPa。

所研究的对象模型中，油液为10号航空油，其密度ρ=850 kg/m3，体积弹性模量β=850 MPa，得波速c=1 km/s。

(3)黏性影响度Ndiss计算公式为

Ndiss=4Lu/(aD2)

(10)

其中，u是液体的动力黏度，Pa·s；当Ndiss>1时，其他影响因素与黏性相比就不是很重要了。管道建模具体依据如图3所示。

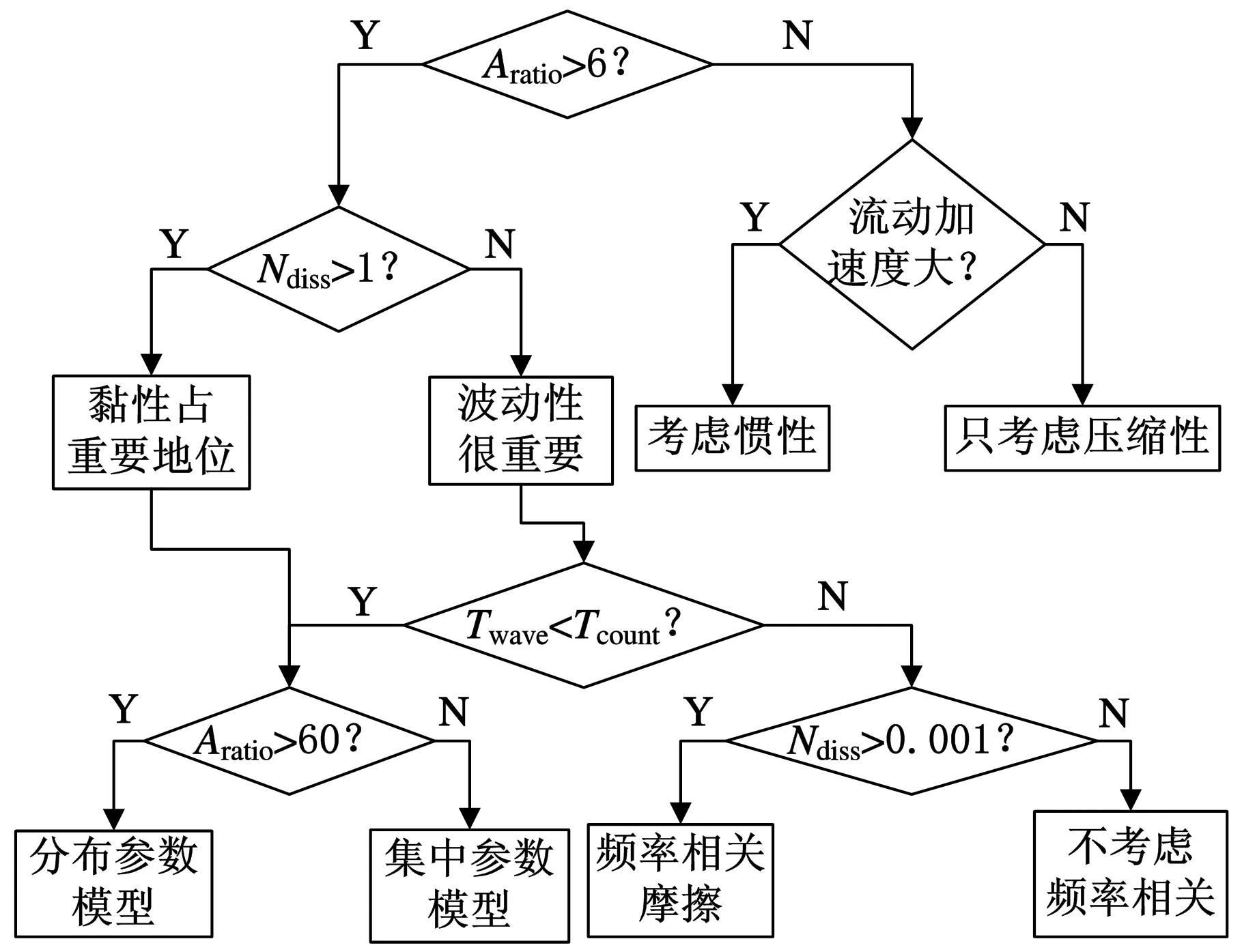
图3　管道建模依据

本文研究对象为特高压断路器液压操动机构，其结构布局简图见图4。主要研究的管道为蓄能器出口至控制阀入口的几条管道。其中，管道1、管道2与另一蓄能器出口两根管道对称分布，管道3为液压缸缸壁上的一段很长的通道；管道4为进入主阀的一段较短的管道。

图4　液压操动机构结构简图

通过分析计算，4条主要管道的长细比均小于6，黏性影响度都大于1，因此管道均采用集中参数模型建立。同时考虑AMESim管道模型的特性，最终管道模型选择如下：管道1选择模型HL03，管道2、管道4选择模型HL01，管道3选择模型HL07。依据上述理论分析，以某超高压断路器的分闸动作为例，建立的AMESim系统综合仿真模型如图5所示。

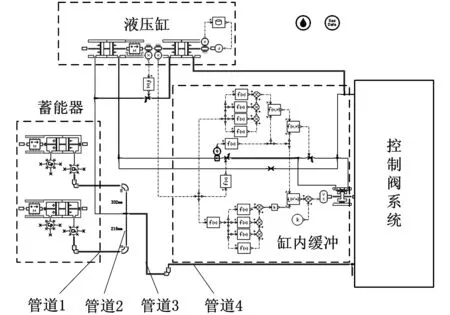
图5　液压操动机构AMESim综合仿真模型

3　计算结果及分析

对图5所示的计算模型进行求解，求解器选择AMESim中的动力学标准自动变步长积分器，误差类型为混合型，收敛容差为10-5，输出打印间隔为10-6，仿真总时间为0.2 s。最后计算得到4条管道的端口压力波动结果如图6所示。

图6　各管道端口压力波动曲线

由图6可以看出，压力波动使得管道内的油液压力不断振荡，且具有较大的振幅，其中管道4的压力波动最为严重，波动峰值最高为33 MPa，最低为31 MPa。管道4为主阀入口处的管道，表明主阀处的压力波动最大，而主阀位于所研究的管道下游，这与理论分析的结果基本一致。

在已建立的管道模型基础上，通过对管道长度以及管道内径这两个主要参数进行变参分析来研究其对管道的压力波动的影响。

3.1管道长度的影响分析

3.1.1对管道3、管道4进行长度方案设计

在保证管道总长不变的情况下，对管道3、管道4进行长度方案设计，见表1。

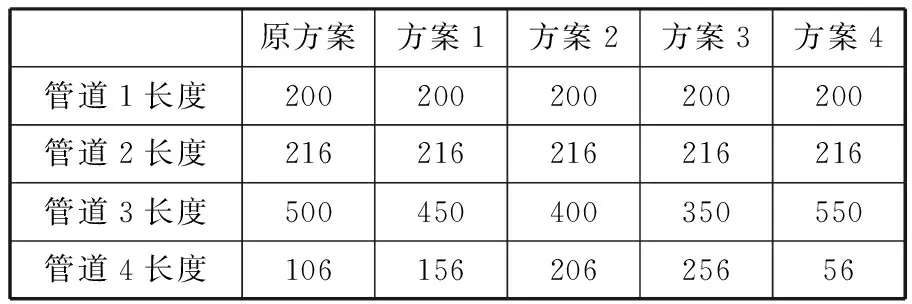
表1　管道3和管道4的长度设计方案　mm

通过仿真计算得到管道4的压力波动在不同设计方案下的对比结果如图7所示。

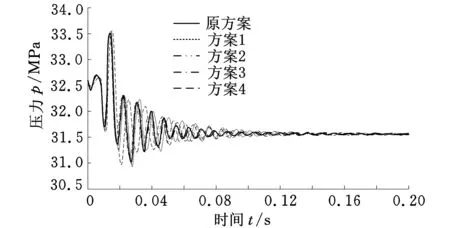
图7　4种设计方案下管道4端口压力的波动情况对比(一)

从图7可以看出，方案2的压力波动最大压力值小于原方案，最小压力值大于原方案，使得波动的压力区间减小，并且方案2压力波动的衰减明显快于其他方案，因此方案2对于减小压力波动有较好的效果。4种方案的压力波动对比结果见表2。

表24种设计方案下压力波动对比(一)

MPa

3.1.2对管道1、管道2进行长度方案设计

在保证管道总长不变的情况下，对管道1、管道2进行长度方案设计，见表3。

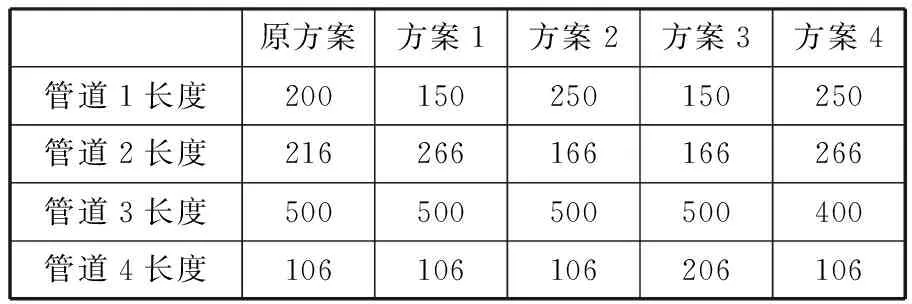
表3　管道1和管道2的长度设计方案　mm

通过仿真计算得到管道4的压力波动在不同设计方案下的对比结果，如图8所示。

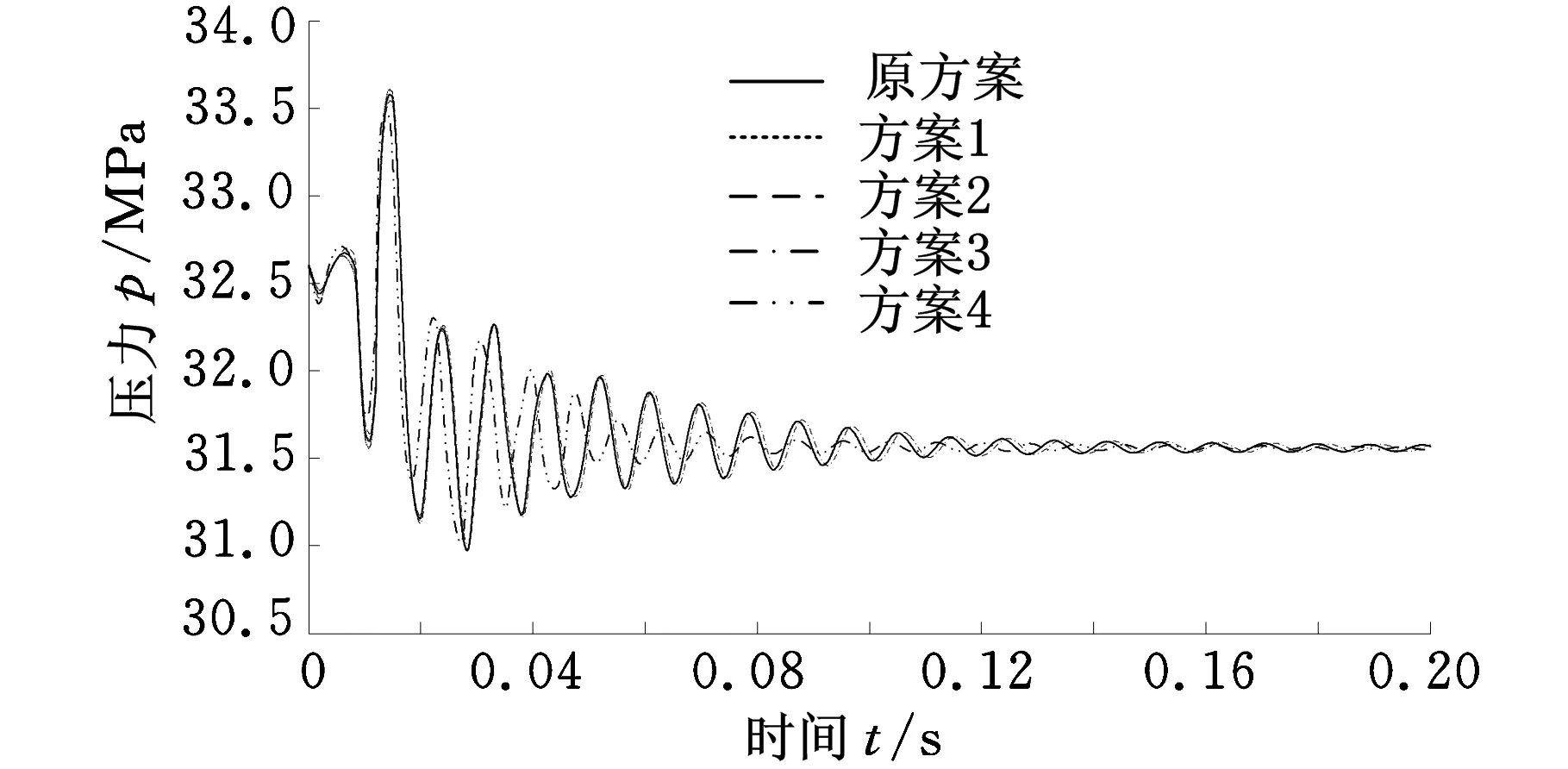
图8　4种设计方案下管道4端口压力的波动情况对比(二)

由图8可以看出，方案4的最大压力值小于原方案，最小压力值大于原方案，压力变化区间减小，并且方案4压力波动衰减明显快于其他方案，因此在保证总长不变的情况下延长管道1和管道2、缩短管道3和管道4对减小压力波动有明显作用。4种方案的压力波动峰值与原方案对比结果见表4。

表4　4种设计方案下压力波动对比(二) MPa

3.2管道内径的影响分析

对4根管道进行内径方案设计，见表5。

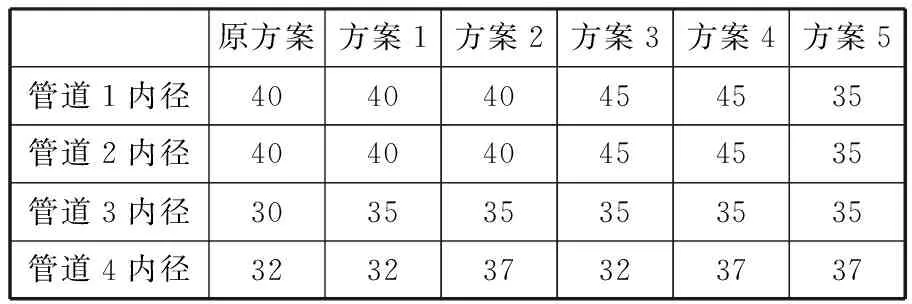
表5　改变管径的设计方案　mm

通过仿真计算得到5种不同设计方案下管道4的压力波动的对比结果，如图9所示。

图9　5种设计方案下管道4端口压力的波动情况对比

由图9可以看出，除原方案外，压力波动曲线基本重合。说明对管道1、管道2进行内径调整对管道波动情况影响不大，主要影响仍在管道3、管道4的内径上。在扩大管道3、管道4内径的基础上能有效减小管道压力波动情况，而管道1、管道2的内径则可根据实际情况选择。压力波动的对比见表6。

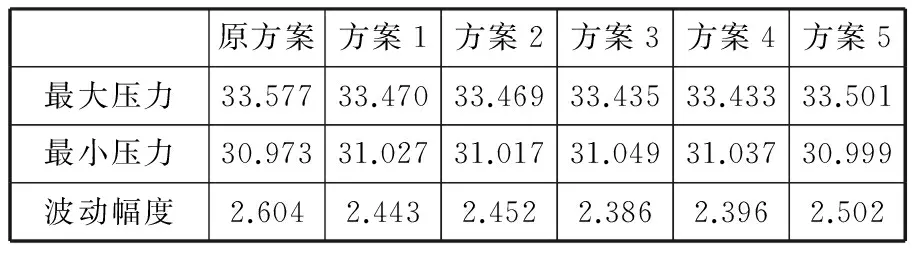
表6　5种设计方案下压力波动对比　MPa

以上结果表明，适当增大管道3、管道4的内径，能有效减小管道的压力波动。由此得出，主要管道内径设计得越大，动态压力的最大值越小，波动越平缓。

3.3管道优化方案设计

通过管道长度和直径的变参数分析，发现管道3和管道4的长度和直径对系统压力波动的影响最大，笔者在参数分析的基础上设计了多种优化方案，可以有效地减小系统的压力波动。

通过对管道3、管道4的长度、内径进行变参分析，得出一组最优优化方案，即增加管道3长度、缩短管道4长度并增大两条管道内径。与原方案进行结果对比，压力波动曲线如图10所示。

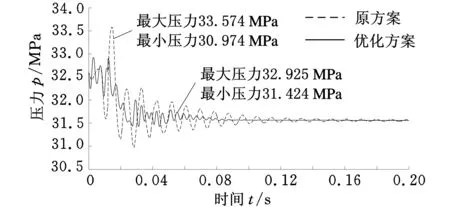
图10　优化设计方案压力波动曲线对比

由图10可以看出，优化方案的压力波动幅度为1.501 MPa，压力波动幅度降低为原方案的57.66%，且压力波动的衰减快于原方案。

4　结语

本文基于AMESim液压系统仿真平台对特高压断路器的管道系统进行压力波动研究。通过管道子模型的合理选取，运用液压系统综合仿真的方法研究了从蓄能器出口到主阀的4条管道压力波动的特性。通过变参数分析，得到了管道长度和内径变化对压力波动影响的量化结果，通过对液压系统中长管道的缩短和短管道的加长、增大管道内径的合理组合方式有效地降低了压力波动幅度，降低幅度超过50%。运用液压系统综合建模的方法，通过管长和内径组合优化设计，对有效地降低液压管道的压力波动幅度具有一定的工程实用价值。

[1]范舜.高压断路器液压操动机构[M].北京：机械工业出版社，1999.

[2]Yoshioka Y.Present Status of Power Circuit Breaker and Its Future[J].IEE J. Transactions on Power and Energy, 2006，126(7): 653-656.

[3]刘伟，杨华勇，徐兵，等.高压断路器液压操动机构管道特性研究[J].农业机械学报，2010,41(1):182-187.

Liu Wei, Yang Huayong, Xu Bing,et al.Pipe Characteristics of High Voltage Circuit Breaker with Hydraulic Operating Mechanism[J].Transactions of the Chinese Society of Agricultural Machinery, 2010,41(1): 182-187.

[4]高钦和.SIMULINK在液压回路动态特性仿真中的应用[C]//全国第二届DSP应用技术学术会议论文.北京，2004: 406-408.

[5]高钦和, 黄先祥, 郭晓松.机液一体化系统中液压管路动态特性的建模与仿真研究[J].中国机械工程，2003, 14(10): 823-825.

Gao Qinhe, Huang Xianxiang, Guo Xiaosong.Research on Dynamic Modeling and Simulation of Fluid-transmission Line in Hydraulic-driven System[J].China Mechanical Engineering, 2003,14(10):823-825.

[6]李松晶,鲍文.采用 MATLAB Simulink 的液压管路瞬态压力脉动分析[J].工程力学，2006, 23(9): 184-188.

Li Songjing, Bao Wen.Analysis of Transient Hydraulic Pressure Pulsation in Pipelines Using MATLAB Simulink[J].Engineering Mechanics,2006,23(9): 194-188.

[7]张洪.基于 MATLAB 的液压管路动态特性的仿真[J]. 液压与气动，2003(9): 28-30.

Zhang Hong.The Simulation for the Dynamic Character of the Hydraulic Pipe Based on MATLAB[J].Chinese Hydraulics & Pneumatics, 2003(9):28-30.

[8]叶达忠,唐新发.特征线法速算有压管道的水击强度及其曲线绘制[J].大众科技, 2009(12): 125-126.

Ye Dazhong, Tang Xinfa.Rapid Calculation of Intensity of Water Hammer in Pressure Pipeline Based on Characteristics Method and Curve Plotting[J].Da Zhong Ke Ji, 2009(12): 125-126.

[9]吴持恭.水力学(下册)[M].北京：高等教育出版社，2003.

[10]齐鄂荣，曾玉红.工程流体力学[M]. 武汉：武汉大学出版社，2005.

[11]车学科.液体推进剂供应管道动态特性研究[D].长沙：国防科学技术大学，2005.

[12]刘鹏.一种气液联合式破碎锤工作性能的建模与仿真研究[D].长沙：中南大学，2012.

(编辑陈勇)

Analysis of Pressure Fluctuation in UHV Breaker Hydraulic Pipeline Based on AMESim

Lai QiweiWu ShijingZhang ZengleiHu Jicai

Wuhan University，Wuhan，430072

With the purpose of settling the impact of hydraulic shock in hydraulic operating system of UHV breaker, energy accumulator and its hydraulic pipeline system served as the research objects. Based on the analysis of pressure fluctuation mechanism，principles of selecting sub-model of pipeline were established. With the simulation of comprehensive model of the hydraulic system using software AMESim, characteristics of pressure fluctuation in the hydraulic pipeline was obtained. Meanwhile，impacts of length and diameter of pipeline on pressure fluctuation were analyzed. The results show that the existing pressure fluctuation amplitude is large, which is not conducive to the stable operation of the system. After combinatorial optimization of length and diameter of pipeline, pressure fluctuation is reduced by over 50%. The adopted research methods have certain theoretical guidance and practical value to optimal design of pipeline system in UHV breaker.

hydraulic pipeline system；pressure fluctuation；parameter optimization；ultra high voltage(UHV) breaker

2014-05-07

国家自然科学基金资助项目(51375350)；湖北省科技厅重点资助项目(2011132094)；国家电网公司科技项目(208239881)

TH137DOI：10.3969/j.issn.1004-132X.2015.07.002

赖奇暐，男，1991年生。武汉大学动力与机械学院博士研究生。主要研究方向为机电液复合传动、机械动力学。巫世晶，男，1963年生。武汉大学动力与机械学院教授、博士研究生导师。张增磊，男，1987年生。武汉大学动力与机械学院博士研究生。胡基才，男，1962年生。武汉大学动力与机械学院副教授。