关于Kronecker积的特征值与奇异值研究

徐富伟，任芳国

（陕西师范大学数学与信息科学学院，陕西西安710062）

关于Kronecker积的特征值与奇异值研究

徐富伟，任芳国

（陕西师范大学数学与信息科学学院，陕西西安710062）

Kronecker积既是一种重要的矩阵乘积又是解矩阵方程的重要工具。利用奇异值分解以及特征值和奇异值的基本性质，研究Kronecker积下的特征值和奇异值问题，获得了Kronecker积A⊗B和B⊗A的行列式和迹的关系，Kronecker和的特征值及一个Hadamard积的不等式。

特征值；奇异值；Kronecker积

Kronecker积是矩阵分析方面研究的主要内容，一直受到有关专家学者的关注［1-14］。文献［1］讨论了Kronecker积下的矩阵秩的等式与不等式，并且因此得到了两个著名线性变换T1（X）=X-AXB和T2（X）=AX-XB值域的维数的上下界；文献［2］定义了两种全新的Kronecker和以及与之相关的算子，讨论了它们的特征值特征向量；文献［3］讨论了Schur函数下Kronecker积的稳定性。基于以前的研究，本文对两个矩阵的Kronecker积的特征值与奇异值及其特征向量和奇异值向量的情况进行了讨论，随后给出了一般矩阵A、B的Kronecker积A⊗B和B⊗A的行列式和迹的关系，并给出Kronecker和的特征值的另一种证法，最后给出一个关于Hadamard积的不等式。

1　预备知识

为了叙述方便，我们对符号约定如下：Cn表示复数域上的n维列向量的集合；A*表示矩阵A的共轭转置矩阵；Mm，n表示m×n阶矩阵的集合；tr（A）是矩阵A的迹；Mn表示n×n阶矩阵的集合，并且本文所涉及到的奇异值都是降幂排序，没有特别说明的符号以参考文献［4］为准。

定义1［4］设A=（aij）∈Mm，n，B=（bij）∈Mp，q，称分块矩阵为A和B的 Kronecker积，记作A⊗B。

定义2［4］A∈Mm，n，A∗A∈Mn的特征值按降序排列，前min｛m，n｝个特征值的算术平方根称为A的奇异值。记作

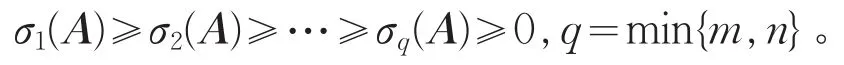
定义3［5］设X∈Mm，n有奇异值

这里q=min｛m，n｝，称

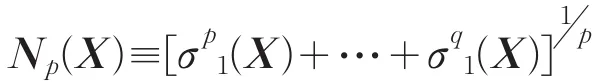
为矩阵X的schatten p-范数，其中1≤p≤∞。

引理1［4］设A∈Mm，n，B∈Mp，q，C∈Mn，k，D∈Mq，r。则（A⊗B）（C⊗D）=（AC）⊗（BD）。

引理2［4］设A∈Mn，B∈Mm。如果λ∈σ（A），并且x∈Cn是对应的特征向量；μ∈σ（B），并且y∈Cm是对应的特征向量。那么λμ∈σ（A⊗B），x⊗y∈Cnm是A⊗B的属于λμ的特征向量。于是，如果

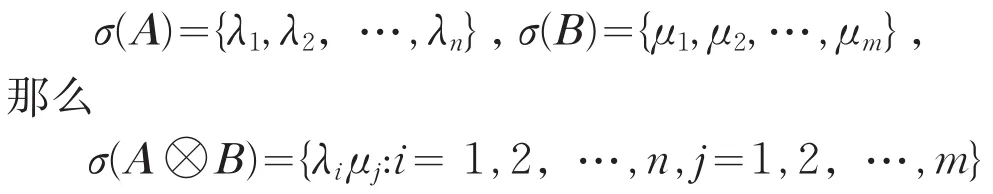
（包含重数）。

特别的，σ（A⊗B）=σ（B⊗A）。

引理3［4］如果A∈Mn，B∈Mm。则

（Ⅰ）det（A⊗B）=（detA）m（detB）n=det（B⊗A）；

（Ⅱ）tr（A⊗B）=tr（A）tr（B）=tr（B⊗A）。

引理4［5］设A∈Mm，n，q=min｛m，n｝，则存在酉矩阵V∈Mm，W∈Mn，使得A=VΣW*，其中Σ的主对角元为A的奇异值，且奇异值

则称VΣW*为A的奇异值分解。

引理5［4］设A∈Mm，n，B∈Mp，q分别有奇异值分解A=V1ΣW1*，B=V2ΣW2*，设rankA=r1，rankB=r2，那么

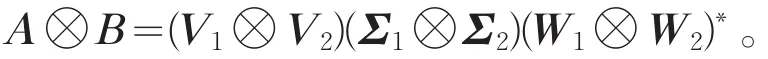
那么A⊗B的非零奇异值为r1r2个正数｛σi（A）σj（B）:1≤i≤r1，1≤j≤r2｝（包括重数），A⊗B的零奇异值的重数为min｛mp，nq｝-r1r2。特别的，A⊗B的奇异值和B⊗A的奇异值相同，并且rank（A⊗B）=rank（B⊗A）=r1r2。

引理6［5］设A∈Mm，n，Ar记为A去掉r行或r列后剩余的子矩阵。那么

σk（A）≥σk（Ar）≥σk+r（A），k=1，2，…，min｛m，n｝对于X∈Mp，q，σj（X）≡0，当j＞min｛p，q｝。

2　定理及其证明

定理1设A∈Mm，n，B∈Mp，q，mp=nq，则

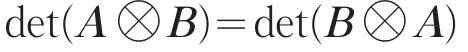
且tr（A⊗B）≠tr（B⊗A）。

证明：当m=n，p=q时，由引理3知定理成立。

当m≠n时，不妨设m＞n，p＜q，则设A和B分别有奇异值分解

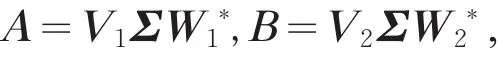
那么

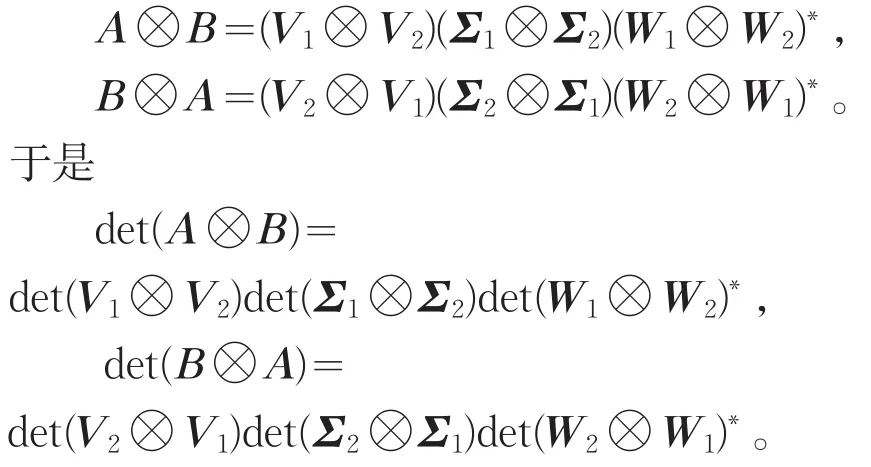
由引理3知

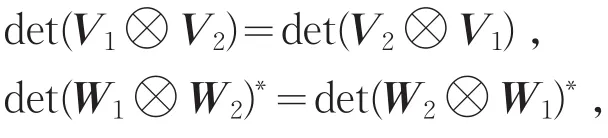
又由引理5知

但是tr（A⊗B）=7≠tr（B⊗A）=9。

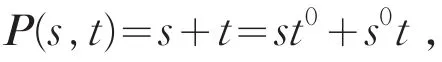
即为Kronecker和，则

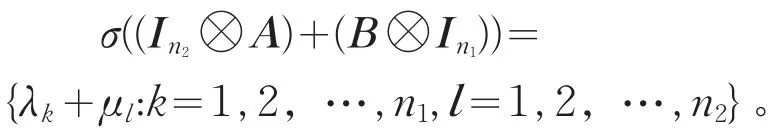
证明：设x∈Cn1是A属于λk的特征向量，y∈Cn2是B属于μl的特征向量，则

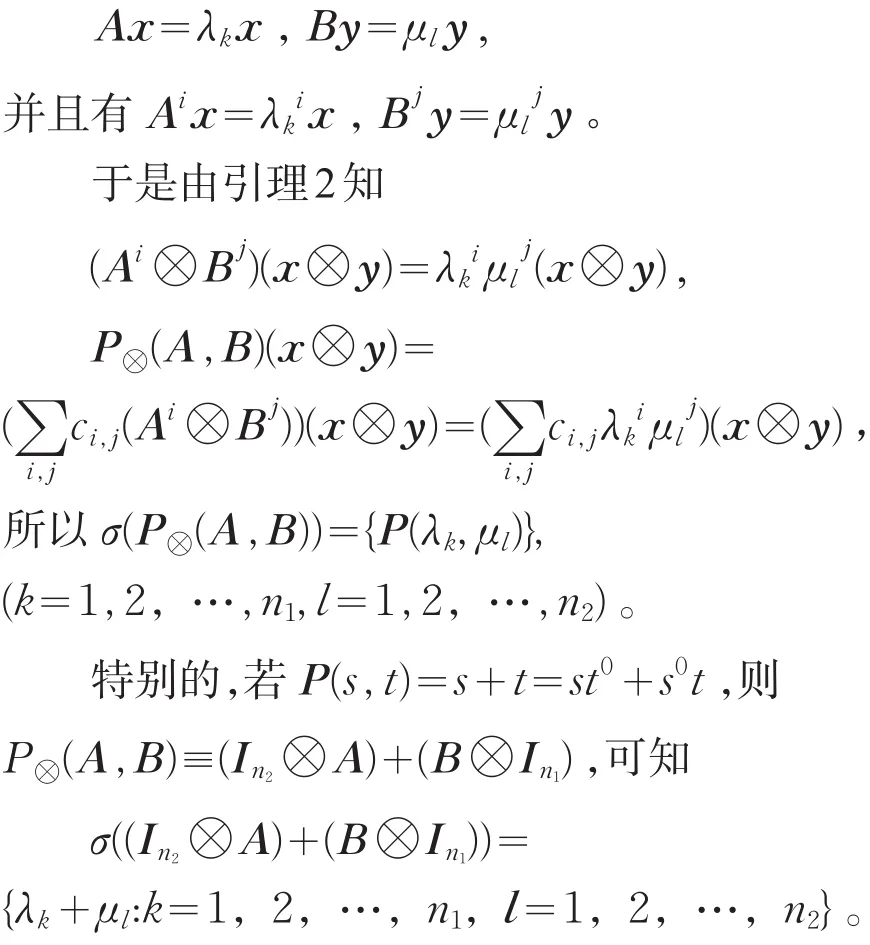
定理3如果｛x1，x21，…，xn｝⊂Cm，

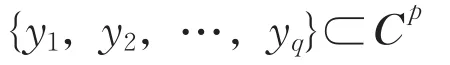
是两个线性无关集，则｛xi⊗yj，i=1，2，…，n，j=1，2，…，q｝是Cmp上的线性无关集。

证明：设A=（x1，x2，…，xn）∈Mm，n，

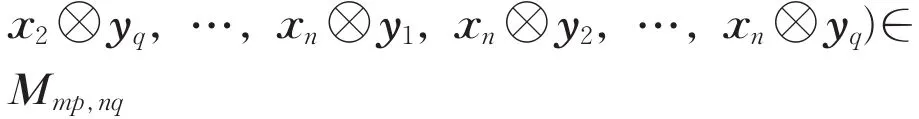
再由引理5知，rank（A⊗B）=rank（B⊗A）=nq，于是A⊗B是列满秩的，因此

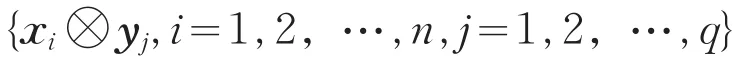
是Cmp上的线性无关集。

定理4设A∈Mm，n，B∈Mp，q分别有奇异值分解A=V1ΣW1*，B=V2ΣW2*，其中

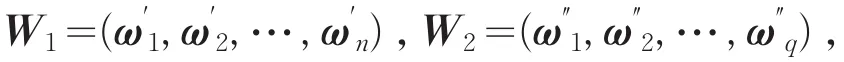
证明：设A和B具有如下的奇异值分解

记V1≡（ν′1，ν′2，…，ν′m），W1=（ω′1，ω′2，…，ω′n），V2≡（ν″1，ν″2，…，ν″p），W2=（ω″1，ω″2，…，ω″q）。

于是由式（1）（2）得

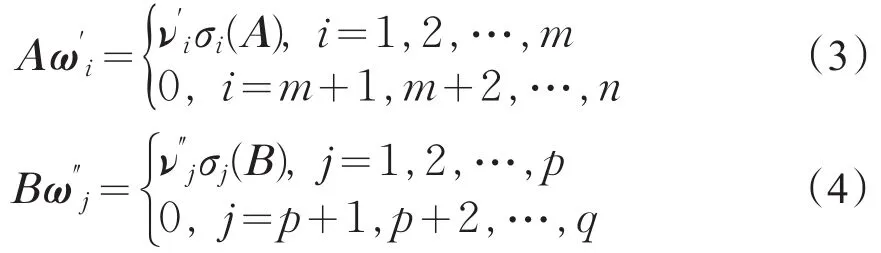
其中ω′i和ω″j分别称为A和B的右奇异值向量。由式（3）（4）得

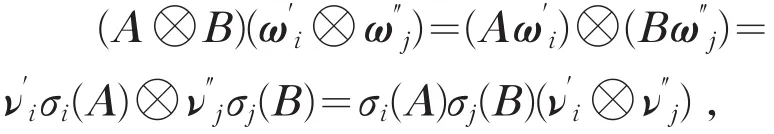
所以（A⊗B）的关于σi（A）σj（B）的右奇异值向量为

定理5设A∈Mm，n，B∈Mr，s，则

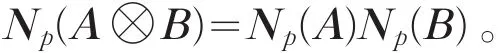
证明：设A的奇异值为

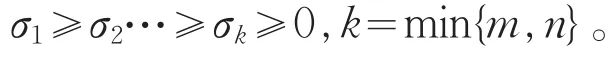
B的奇异值为

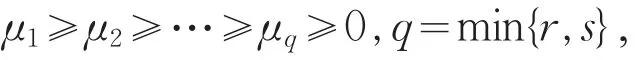
则由引理5有A⊗B的奇异值为

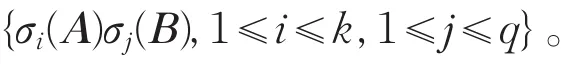
从而

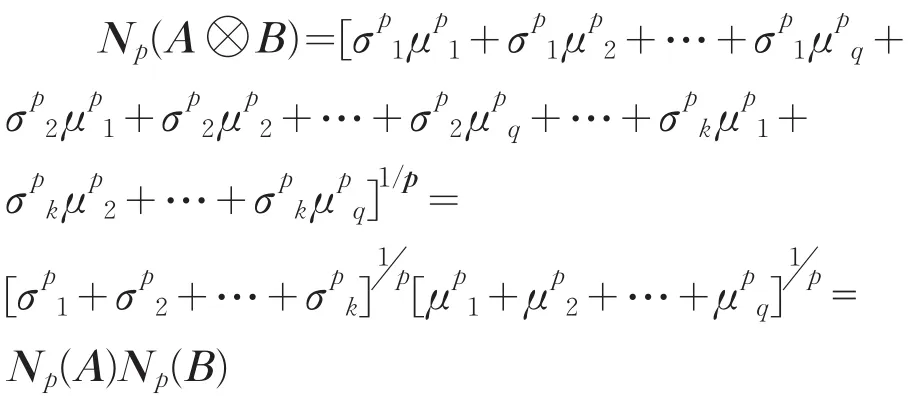
最后利用Kronecker积给出一个有关Hadamard积的不等式。

定理6A，B∈Mm，n，‖·‖为矩阵的谱范数，那么。

证明：‖A‖2和‖B‖2分别为A，B的谱范数，即A，B的最大奇异值。由定理5知

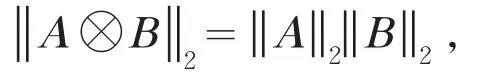
又A∘B是A⊗B的一个子矩阵，所以由引理6得，

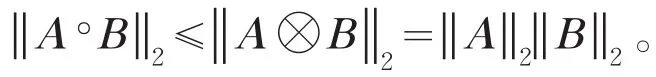
3　结论

Kronecker积具有丰富的性质，本文只就Kronecker积A⊗B和B⊗A的行列式和迹的关系，Kronecker和的特征值及一个Hadamard积的不等式进行了讨论。

［1］CHUAI J，TIAN Y.Rank equalities and inequalities for Kronecker products of matrices with applications［J］.Applied Mathematics and Computation，2004，150：129-137.

［2］JUNE F，JAMES L.Spectral properties of sums of certain Kronecker products［J］.Linear Algebra and Its Applications，2009，431：1691-1701.

［3］EMMANUEL B，ROSA O，MERCEDES R.The stability of the Kronecker product of Schur functions［J］.Journal of Algebra，2011，331：11-27.

［4］HORN R A，JOHNSON C R.Topics in matrix analysis［M］. Cambridge：Cambridge University Press，1991.

［5］HORN R A，JOHNSON C R.Matrix analysis［M］.Cambridge：Cambridge University Press，1990.

［6］REGALIA P，MITRA S.Kronecker products and signal processing applications［J］.SIAM Review，1989，31：586-613.

［7］BHATIA R，ROSENTHAL P.How and why to solve the operator equation AX-XB=Y［J］.Bulletin of the London Mathematical Society，1997，29：1-21.

［8］VAN LOAN C F.The ubiquitous Kronecker product［J］.Computational andApplied Mathem-atics，2000，123：85-100.

［9］MARKO HUHTANEN.Real linear Kronecker product operations［J］.Linear Algebra and Its Applications，2006，418：347-361.

［10］DELVAUX S，VAN BAREL M.Rank-deficient submatrices of Kronecker products of Fourier atrices［J］.Linear AlgebraApplications，2007，426：349-367.

［11］KILMER M E，NAGY J G.Kronecker product approximations for dense block matrices Toep-Litz-plus-Hankel Numer［J］.LinearAlgebraApplications，2007，14：581-602.

［12］YAN Z D，WANG W.Equitable coloring of Kronecker products of complete multipartite graphs and complete graphs［J］. DiscreteApplied Mathematics，2014，162：328-333.

［13］LOTOTSKY S V.Simple spectral bounds for sums of certain Kronecker products［J］.Linear Algebra and Its Applications，2015，469：114-129.

［14］PRANAVA K J，JONATHAN D H.Cycle Kronecker products that are representable as optimal circulants［J］.Discrete Applied Mathematics，2015，181：130-138.

Study on Eigenvalue and Singular Value of Kronecker Product

XU Fuwei，REN Fangguo
（College of Mathematics and Information Science，Shaanxi Normal University，Xi'an 710062，Shaanxi，China）

Kronecker product is an important matrix product and useful tool in solving matrix equations.According to the basic properties of eigenvalue and singular value as well as the singular value decomposition，we study eigenvalue and singular value of Kronecker product.Firstly，the relations of the determinant and trace ofA⊗BandB⊗Aare obtained.Secondly，the eigenvalue of Kronecker sum and a Hadamard inequality are given.

eigenvalue；singular value；kronecker product

O151.21

A

1672-2914（2015）06-0041-04

2015-07-06

国家自然科学基金项目（11471200）。

徐富伟（1993-），男，河南驻马店市人，陕西师范大学数学与信息科学学院硕士研究生，研究方向为矩阵论。

任芳国，副教授，E-mail:rfangguo@snnu.edu.cn。