度量空间中的半连续函数

张永锋

（咸阳师范学院数学与信息科学学院，陕西咸阳712000）

［数理科学与信息科学研究］

度量空间中的半连续函数

张永锋

（咸阳师范学院数学与信息科学学院，陕西咸阳712000）

研究度量空间中函数的半连续性，给出了半连续性的一些等价刻画及半连续函数的若干重要性质。

度量空间；半连续函数；等价刻画

函数及其各种推广是分析学研究的主要对象，函数的连续性是一个重要的分析概念，半连续函数是连续函数的自然推广，在许多方面都有重要的应用。关于半连续函数的定义、等价条件与性质，许多作者进行了研究。文献［1-2］给出了直线上半连续函数的定义，研究了半连续函数的等价条件与性质，建立了直线上半连续函数的若干命题；文献［3-7］在直线上半连续函数定义基础上，利用实数完备性理论中的部分定理给出了闭区间上半连续函数的有界性与最值性结论的多种不同证明方法，同时给出了判断函数在闭区间上是半连续的充要条件；文献［8］利用连续归纳法证明了半连续函数的几个性质；文献［9］通过研究凸函数与半连续函数的关系，给出了凸函数的一个与上半连续性相结合的等价关系。本文继续讨论半连续函数，首先给出度量空间中半连续函数的定义，然后证明函数为半连续函数的几个等价条件，同时给出半连续函数的若干重要性质，推广了直线上相应结论。

文中恒用X表示度量空间，用d表示距离，用E表示X中的点集，用f（x）表示实函数。

1　半连续函数的定义

设（X，d）为度量空间，E⊂X，f（x）是定义在E上的实函数，x0∈E。f（x）在x0处连续是指［10］：对任意给定的正数ε，存在正数δ，使得当x∈U（x0，δ）⋂E时，有f（x）∈U（f（x0），ε），即

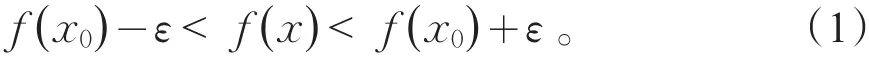
如果将不等式（1）减弱，只使其中的一个不等式成立，那么就是所谓的半连续。

定义1设f（x）是定义在点集E上的函数，x0∈E。若对任给的正数ε，存在正数δ，使得当x∈U（x0，δ）⋂E时，有

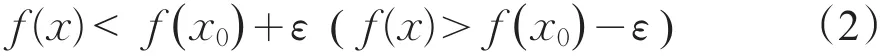
则称f（x）在x0处上（下）半连续。若函数f（x）在E上每一点处都上（下）半连续，则称f（x）在E中上（下）半连续。

上半连续与下半连续统称为半连续。

例1设D（x）为Dirichlet函数，则函数f（x）=xD（x），当x＞0时在有理点处上半连续，但不下半连续，在无理点处下半连续，但不上半连续；当x＜0时情况恰恰与此相反；在x=0处既上半连续，又下半连续，从而由下面的推论1知在x=0处连续。

由定义1推出如下推论：

推论1设f（x）是定义在点集E上的函数，x0∈E。则f（x）在x0处连续的充要条件是：f（x）在x0处既上半连续，又下半连续。

容易证明（见定理3）：若函数f（x）在x0处下半连续，则-f（x）在x0处上半连续。因此，下面只讨论上半连续。

2　半连续函数的等价条件

下面讨论上半连续的等价描述。

定理1设f（x）是定义在点集E上的函数，x0∈E。则下列命题是等价的：

（Ⅰ）f（x）在x0处上半连续；

（Ⅲ）对任意点列｛xn｝⊂E，xn→x0（n→∞），必有f（xn）≤f（x0）；

M（δ）=sup｛f（x）|x∈U（x0，δ）⋂E｝；

（Ⅴ）对∀A＞f（x0），∃δ＞0，使得当x∈U（x0，δ）⋂E时，有f（x）＜A。

证明：（Ⅰ）⇒（Ⅱ）。由假设可知，任给正数ε，存在正数δ，当x∈U（x0，δ）⋂E时，有

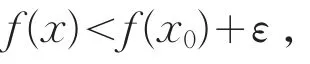
于是

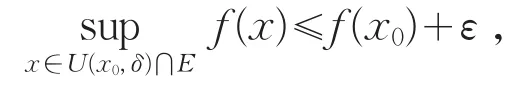
再由ε＞0的任意性，得（Ⅱ）成立。

（Ⅱ）⇒（Ⅲ）。假设存在点列｛xn｝⊂E， xn→x0（n→∞），使。记

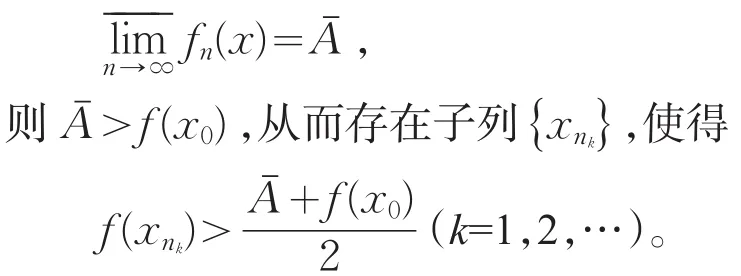
由于xn→x0（n→∞），故。

因此

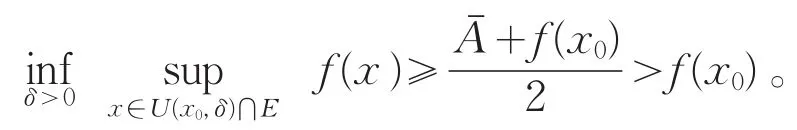
这与己知条件（Ⅱ）矛盾。

（Ⅲ）⇒（Ⅰ）。假设f（x）在x0处不上半连续，则存在某正数ε0，对任意，存在

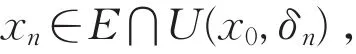
使f（xn）≥f（x0）+ε0（n=1，2，…）。显然，点列｛xn｝⊂E，且xn→x0（n→∞），但由上式，得

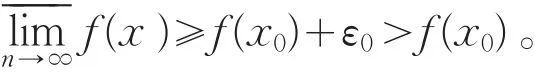
这与已知条件（Ⅲ）矛盾。

（Ⅰ）⇒（Ⅳ）。因f（x）在x0处上半连续，所以对∀ε＞0，∃δ′＞0，当x∈U（x0，δ′）⋂E时，有

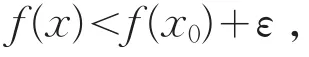
从而当0＜δ＜δ′时，有

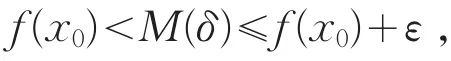
故|M（δ）-f（x0）|≤ε，因此M（δ）=f（x0）。

（Ⅴ）⇒（Ⅰ）。对∀ε＞0，令A=f（x0）+ε，则∃δ＞0，使得当x∈U（x0，δ）⋂E时，有

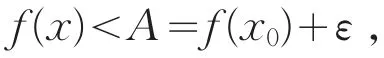
即（Ⅰ）成立。

定理2设f（x）是定义在X中闭集E上的函数，则f（x）在E中上半连续的充要条件是：对任意c∈（-∞，+∞），集合F（c）=｛x|x∈E，f（x）≥c｝为X中闭集。

证明：必要性。设x0为F（c）的任一聚点，则存在点列｛xn｝⊂F（c），使xn→x0（n→∞），此时｛xn｝⊂E。因E是闭集，故x0∈E。由于｛xn｝⊂F（c），故f（xn）≥c（n=1，2，…），从而有。又因为f（x）在x0处上半连续，故由定理1（Ⅲ），有

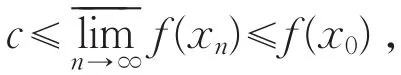
所以x0∈F（c），因此F（c）为闭集。

充分性。假设f（x）不在E中上半连续，则至少存在一点x0∈E，f（x）在x0处不上半连续。于是存在某正数ε0，对任意，存在xn∈E⋂U（x0，δn），使

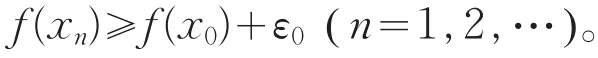
取常数c，使f（x0）＜c＜f（x0）+ε0。根据F（c）的定义，有｛xn｝⊂F（c），但x0F（c）。

又因为xn→x0（n→∞），且F（c）为闭集，故应有x0∈F（c），矛盾。

推论2函数f（x）在度量空间X中上半连续的充要条件是：对任意c∈（-∞，+∞），集合F（c）=｛x|f（x）≥c｝为X中闭集。

3　半连续函数的性质

定理3（局部保号性）设f（x）是定义在点集E上的函数，x0∈E。若f（x）在x0处上半连续，且f（x0）＜0，则对任何正数r＜-f（x0），存在正数δ，使得当x∈U（x0，δ）⋂E时，有f（x）＜-r。

证明：对任何正数r＜-f（x0），由于f（x）在x0处上半连续，因此对正数ε=-［f（x0）+r］，存在正数δ，使得当x∈U（x0，δ）⋂E时，有

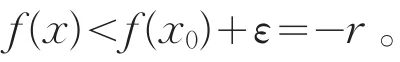
定理4（四则运算性质）设E为X中点集，x0∈E。

（Ⅰ）若函数f（x），g（x）在x0处上（下）半连续，则f（x）+g（x）在x0处上（下）半连续；

（Ⅱ）若f（x）在x0处上（下）半连续，则-f（x）在x0处下（上）半连续；

（Ⅲ）若f（x），g（x）在x0处上半连续，且f（x）＞0，g（x）＞0，x∈E（或f（x），g（x）在x0处下半连续，且f（x）＜0，g（x）＜0，x∈E），则f（x）·g（x）在x0处上半连续；若f（x）在x0处上半连续，且f（x）＞0，x∈E，g（x）在x0处下半连续，且g（x）＜0，x∈E。则f（x）·g（x）在x0处下半连续；

（Ⅳ）若f（x）在x0处上（下）半连续，且f（x）＞0，x∈E，则在x0处下（上）半连续。

证明：由定义1，（Ⅰ）、（Ⅱ）显然成立。

（Ⅲ）只证：若f（x），g（x）在x0处上半连续，且f（x）＞0，g（x）＞0，x∈E，则f（x）·g（x）在x0处上半连续。对任意｛xn｝⊂E，xn→x0（n→∞），因为f（x），g（x）在x0处上半连续，由定理1（Ⅲ）有

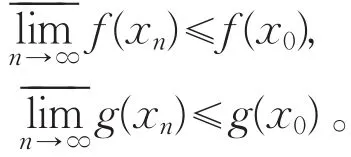
又因为f（xn）＞0，g（xn）＞0（n=1，2，…），故

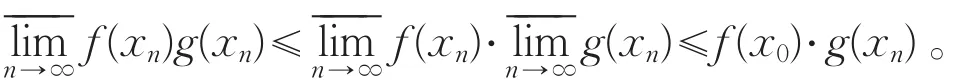
再由定理1（Ⅲ）充分性，得f（x）g（x）在x0处上半连续。

（Ⅳ）只证：若f（x）在x0处下半连续，且f（x）＞0，x∈E，则在x0处上半连续。对任意｛xn｝⊂E，xn→x0（n→∞），因为f（x）在x0处下半连续，故（参照定理1可证）。又f（xn）＞0（n=1，2，…），故

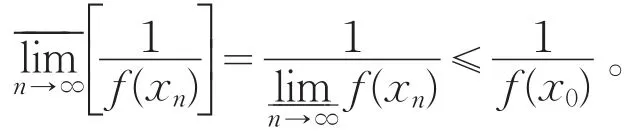
定理5（复合函数半连续性）设（X，d），（Y，ρ）是度量空间，E⊂X，x0∈E。g（x）是E到Y中的映照，f（y）是在D=g（E）⊂Y上有定义的实函数。若g（x）在x0∈E处连续，f（y）在y0=g（x0）∈D处上（下）半连续，则f（g（x）在x0处上（下）半连续。

证明：对任意｛xn｝⊂E，xn→x0（n→∞），则｛g（xn）｝⊂D。因g（x）在x0处连续。故

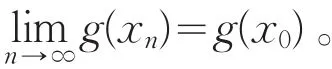
又f（y）在y0=g（x0）处上半连续，由定理1（Ⅲ），知f（g（xn）≤f（g（x0）。又由定理1（Ⅲ）知，f（g（x））在x0处上半连续。下半连续性类似可证。

定理6（有界性）设E是X中的紧集。若函数f（x）在E中上半连续，则f（x）在E有上界，即存在常数M，使得当x∈E时，有f（x）≤M。

证明：对任意x∈E，因f（x）在x处上半连续，故对ε=1，存在正数δx，当x′∈U（x，δx）⋂E时，有f（x′）＜f（x）+1。记F=｛U（x，δx）|x∈E｝，则F是E的开覆盖。因为E是紧集，故F中存在有限子覆盖。设其为U（xi，δxi）（i=1，2，…，k）。记，则当x′∈E时，有f（x′）≤M。

定理7（最大值性）设E是X中的紧集。若函数f（x）在E中上半连续，则f（x）在E上有最大值（即存在x0∈E，使得。

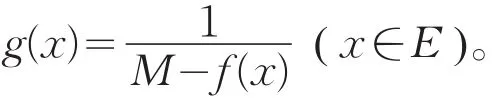
由定理4，g（x）在E中上半连续（因M-f（x）＞0，x∈E且M-f（x）在E中下半连续）。又由定理6，g（x）在E上有上界，于是取正数K，使得当x∈E时有g（x）＜K，即

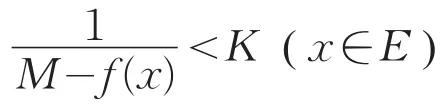
从而可得

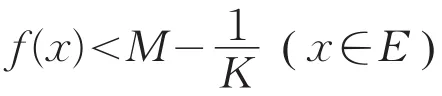
定理8（有下界性）设E是完备度量空间X中的开集。若函数f（x）在E中上半连续，则必存在闭邻域S⊂E，使f（x）在S上有下界。

证明：反正法。假设对任意闭邻域

f（x）总在S上无下界，则存在x1∈E，使得f（x1）＜-1。因为f（x）在x1处上半连续，由局部保号性（定理3），得存在正数δ1（不妨令），使得

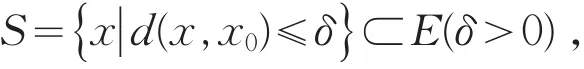
S1=｛x|d（x1，x）≤δ1｝⊂E，且x∈S1时，有

f（x）＜-1。由于f（x）在E中任何闭领域上无下界，故对S1，存在x2∈S1，使得f（x2）＜-2。因为

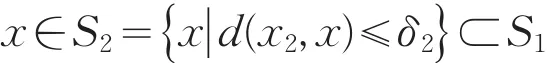
f（x）在x2处上半连续，又由局部保号性，存在正数δ2（不妨令），使得时，有f（x）＜-2。如此继续进行下去，得到一列闭域Sn=｛x|d（xn，x）≤δn｝（n=1，2，…），满足

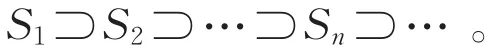
定理9（极限性质）设｛fn（x）｝是点集E中的一列上半连续函数，且在E上有

fn（x）≥fn+1（x）（n=1，2，…（）单调递减列）。

证明：对任意x0∈E，因。故对任意正数ε，存在正整数N，当n≥N时，有。由于fN（x）在x0处上半连续，于是存在正数δ，当x∈U（x0，δ）⋂E，有

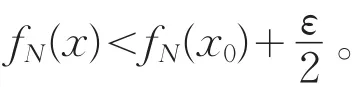
又fn+1（x）≤fn（x）（n=1，2，…），故f（x）≤fN（x），因此，当x∈U（x0，δ）⋂E时，

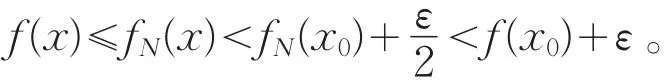
所以f（x）在x0处上半连续，由x0∈E的任意性，f（x）在E中上半连续。

推论3设｛fn（x）｝是点集E上的一列连续函数，且在E上有fn+1（x）≤fn（x）（n=1，2，…）。若，则f（x）在E中上半连续。

实际上，在一定意义下，推理3的逆命题也成立，这就是下面的定理。

定理10设E是有界集，若函数f（x）在E中上半连续且在E上有上界，则存在E上一个实值连续函数列｛fn（x）｝，使得fn+1（x）≤fn（x）（n=1，2，…）且，x∈E。

证明：因f（x）在E上有上界且E为有界集，故对任意正整数n

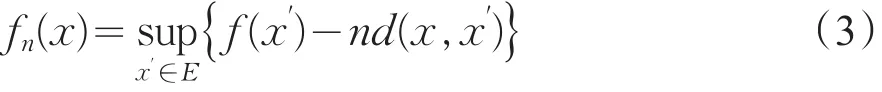
在E上有限，由于

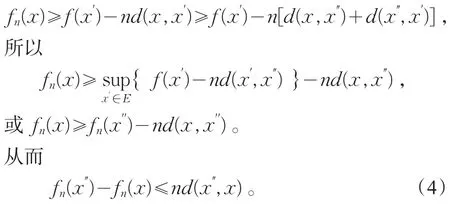
因为式（4）对任意x，x″∈E都成立。因此x，x″互换也成立，于是便得

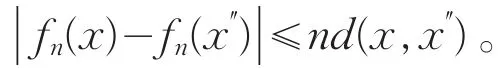
所以fn（x）在E上连续。因为

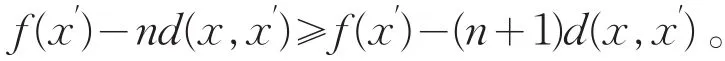
故fn（x）≥fn+1（x）（n=1，2，…），即｛fn（x）｝在E上单调递减。由式（3）可得

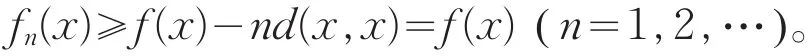
故｛fn（x）｝在E上有下界f（x），因此｛fn（x）｝在E上收敛。记x∈E，则

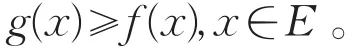
下面证明f（x）=g（x），只需证明

g（x）≤f（x），x∈E。对任意x0∈E，由于f（x）在x0处上半连续，故对任给正数ε，存在正数δ=δ（ε，x0），当x∈U（x0，δ）⋂E时，有

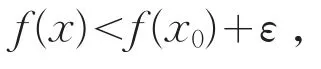
因此，当x∈U（x0，δ）⋂E时，对一切n，有另一方面，当x∈E且d（x，x0）≥δ时，

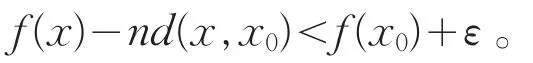
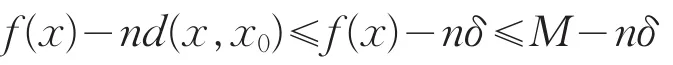
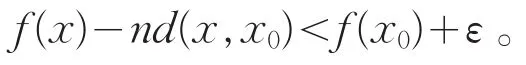
于是当n充分大时，有

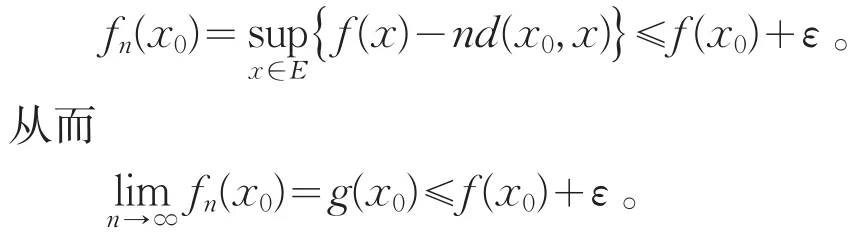
由正数ε的任意性，知g（x0）≤f（x0）。由x0∈E的任意性知g（x）≤f（x），x∈E。

推论4函数f（x）在紧集E中上半连续的充要条件是：E中存在一个单调递减连续函数列｛fn（x）｝（fn+1（x）≤fn（x）n=1，2，…，x∈E），使得

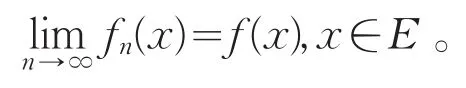
证明：必要性：因E是紧集，故E有界。又f（x）在E中上半连续，由定理6知，f（x）在E上有上界，于是由定理10，结论成立。

充分性：由推论3得。

上面讨论了上半连续函数的等价条件与性质，对于下半连续函数，也有与上述定理相对应的结果，并且由下半连续与上半连续的关系，不难写出下半连续函数的相应定理，同时它们的证明也非常相似，这里不再叙述。

［1］王国才.半连续函数性质探讨之我见［J］.铜仁学院学报，2007，1（6）:100-103.

［2］许万银，闫彦宗.函数半连续问题的若干讨论［J］.宜宾学院学报，2003（3）:47-49.

［3］古小敏.关于半连续函数的一些注记［J］.乐山师范学院学报，2008，23（12）:22-23.

［4］徐运动.关于半连续函数若干性质［J］.鄂州大学学报，2002，9（4）:46-47.

［5］王春雨，佟玲.关于半连续函数性质的一点注记［J］.天津理工大学学报，2007，23（4）:59-60.

［6］庄中文.上半连续函数的充要条件［J］.安顺学院学报，2010，12（2）:77-78.

［7］刘丽波，徐杰.下半连续函数的充要条件［J］.吉林化工学院学报，2008，25（1）:86-88.

［8］郭伟艳，张国才.连续归纳法在半连续函数上的应用［J］.牡丹江大学学报，2007，16（10）:50-60.

［9］黄金莹，赵宇.凸函数与半连续函数的关系［J］.数学的实践与认识，2010，40（13）:153-159.

［10］程其襄，张奠宙.实变函数与泛函分析基础［M］.北京:高等教育出版社，2010.

Semi-Continuous Functions in Metric Spaces

ZHANG Yongfeng
（School of Mathematics and Information Science，Xianyang Normal University，Xianyang 712000，Shaanxi，China）

In this paper，we study the semi-continuous function in a metric space.We obtain several equivalent characterizations of semi-continuity and some properties of it.

metric space；semi-continuous function；equivalent characterization

O174

A

1672-2914（2015）06-0028-05

2015-04-20

张永锋（1957-），男，陕西淳化县人，咸阳师范学院数学与信息科学学院教授，研究方向为基础数学。