一类具有化感作用竞争模型的定性分析

王欢，王艳娥

（陕西师范大学数学与信息科学学院，陕西西安710062）

一类具有化感作用竞争模型的定性分析

王欢，王艳娥

（陕西师范大学数学与信息科学学院，陕西西安710062）

研究在Dirichlet边界条件下一类具有化感作用的竞争模型。采用局部分歧理论构造分歧解的结构，并给出分歧解的稳定性条件。利用全局分歧理论证明局部分歧可延拓为全局分歧。结果表明，该全局分支连接了模型的两个半平凡分支。从生物学角度看，当物种间的化感作用满足一定条件时，两物种可共存。

化感作用；分歧理论；竞争模型

在水生生态系统中，浮游植物群落分布特征的研究是一个重要课题。浮游植物密度和数量的变化不仅受到自然条件、营养物质等因素的影响，而且与种群间的化感作用密切相关。Rice将化感作用较完整的定义为，植物或微生物的代谢分泌物对环境中其他植物或微生物有利或不利的影响［1］。目前，关于带有化感作用竞争模型的研究主要集中于常微分系统［2-5］，考虑到水体是不断流动的，化感物质容易在水中溶解、稀释和迁移，研究带有化感因子的反应扩散系统具有更加现实的意义。本文考虑如下一类具有化感作用的反应扩散系统∇

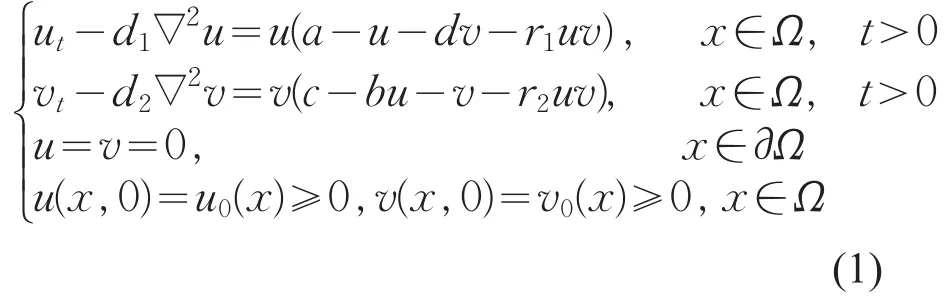
其中∇2为Laplace算子，Ω为Rn中具有光滑边界的有界开区域，d1，d2为扩散系数，u，v分别代表了两个浮游物种的种群密度，a，c是两个物种的内在生长率，d，b分别是第一个物种和第二个物种的种间竞争率，r1，r2分别代表了第一个物种和第二个物种释放化感物质的速率。文献［6］讨论了带有周期系数的反应扩散系统周期解存在性和渐近行为。文献［7］利用上下解方法研究了时滞抛物方程稳态解的渐近行为。本文将主要研究式（1）对应的平衡态问题

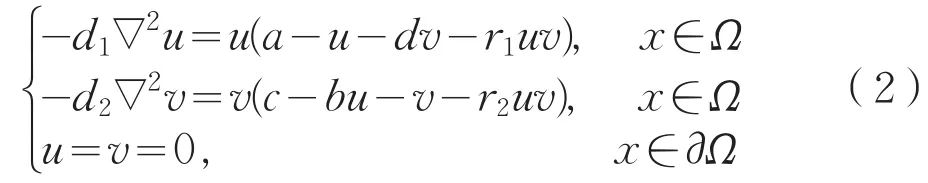
正解的存在性与稳定性。

1　预备知识

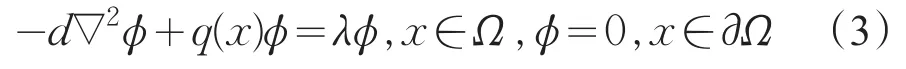
的所有特征值可排列为

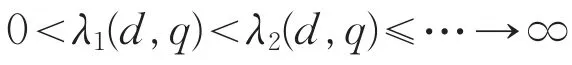
相应的特征函数是ϕ1，ϕ2，…，由变分原理［8］知，其主特征值为

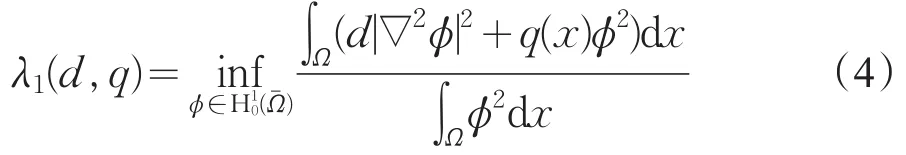
对应的特征函数是ϕ1＞0（x∈）。若q1（x）≥q2（x），x∈，则λj（d，q1）≥λj（d，q2）（j≥1）。又若q1（x）≠q2（x），则λj（d，q1）＞λj（d，q2）（j≥1）。记λ1（1，0）=λ0。显然λ1（d，q）是关于q递增的。

考虑非线性边值问题

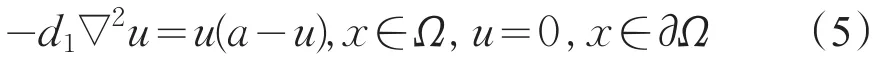
由文献［9］中定理2.3.28知，若a＞d1λ0，则式（5）有唯一正解，记为θa，且θa关于a是递增的，并有0＜θa＜a。因此，当a＞d1λ0时，系统（2）存在唯一的半平凡解（θa，0）；当c＞d2λ0时，系统（2）存在唯一的半平凡解（0，θc）。

下面给出系统（2）非负解的一个先验估计。

引理1若（u，v）是系统（2）的非负解，且u，v不恒为0，则有

（Ⅰ）0＜u＜θa，0＜v＜θc；

（Ⅱ）a＞d1λ0，c＞d2λ0；

（Ⅲ）对于固定的a＞d1λ0，c有界。

证明：（Ⅰ）若（u，v）是系统（2）的非负解，u，v不恒为0，由极值原理知u＞0，v＞0。由于（θa，0）是系统（2）的半平凡解，故-d1∇2θa=θa（a-θa）。而在Ω上有

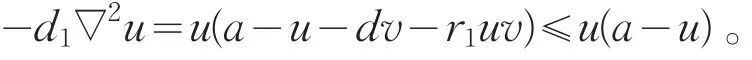
对于下列问题

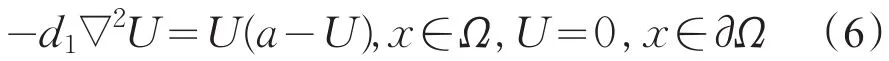
易知u是式（6）的一个下解，U¯=a是式（6）的一个上解，故u＜U=θa。同理可证v＜θc。

（Ⅱ）对于系统（2）的第一个方程两边同时乘以u，在Ω上积分，并使用Green公式得

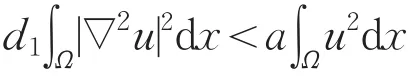
另一方面，利用特征值的变分原理可得

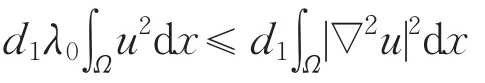
从而a＞d1λ0。同理可证c＞d2λ0。

（Ⅲ）假设存在点列｛（ci，ui，vi）:i∈N+｝满足，其中（ui，vi）为当c=ci时式（2）的正解，则

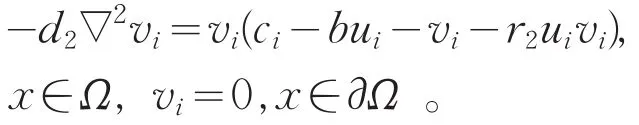
因此，ci=λ1（d2，bui+vi+r2uivi）。由ci→∞及结合式（4）知，bui+vi+r2uivi→∞在Ω上几乎处处成立。又由于ui＜θa，必有vi→∞在Ω上几乎处处成立。另一方面，由式（2）第二个方程

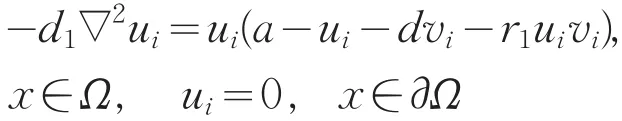
知a=λ1（d1，ui+dvi+r1uivi）。考虑到在Ω上几乎处处有vi→∞，则a→∞，矛盾，从而结论成立。

2　局部分歧

固定a＞d1λ0，取c为分歧参数，从半平凡解分支｛（c，θa，0）:c∈R+｝出发，构造系统（2）的正解。令ω=θa-u，χ=v，则0≤ω≤θa，0≤χ≤θc，且（ω，χ）满足

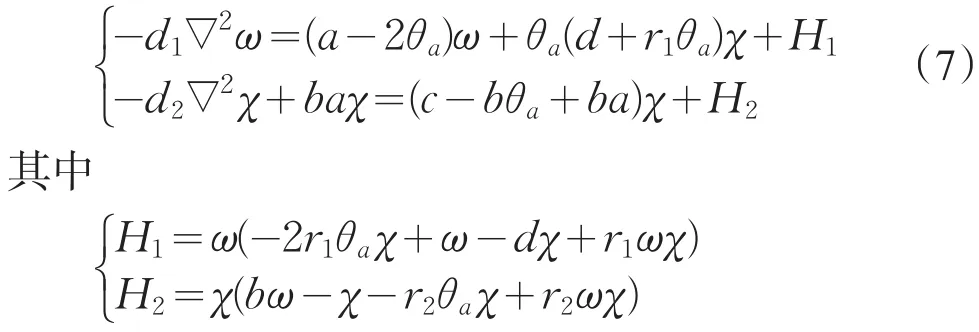
易见，（H1，H2）=H（ω，χ）是连续的，且H（0，0）=0。令K1，K2分别是-d1∇2，-d2∇2+ba在中的逆算子，则方程（7）等价于

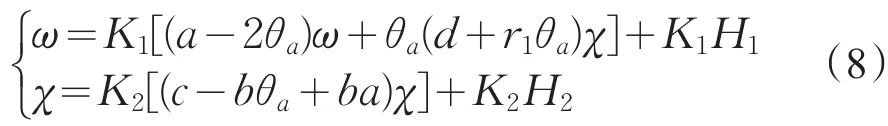
定义算子T:R+×X→X为

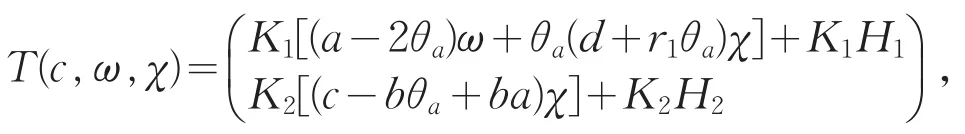
则T（c，ω，χ）为X上的可微紧算子。令F（c，ω，χ）=（ω，χ）-T（c，ω，χ），则F（c，ω，χ）满足0＜ω＜θa，0＜χ＜θc的零点恰好为系统（2）的非负解。

令μ1是下列特征值问题

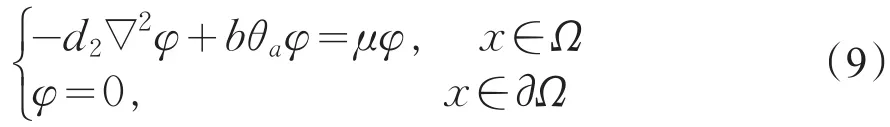
的主特征值，对应的特征函数为φ1＞0，且可规范化为||φ1||2=1。

定理1若a＞d1λ0固定，则（μ1，θa，0）为系统（2）的分歧点，且在（μ1，θa，0）的邻域内，系统（2）存在正解，其中μ1由式（9）给出。

证明：记F（c，ω，χ）关于（ω，χ）在（0，0）点的Frechet导数为L（c，0，0）=D（ω，χ）F（c，0，0），则

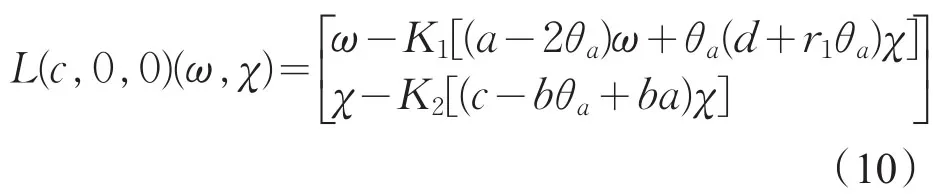
因此，L（c，0，0）（ω，χ）=0等价于

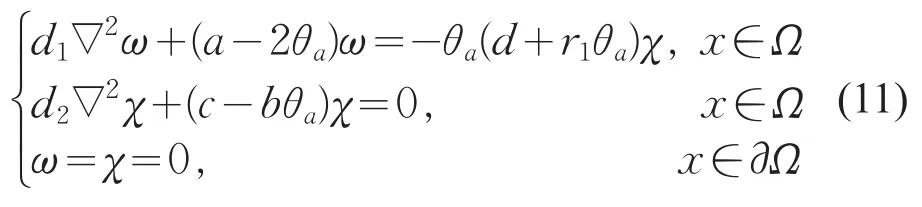
取c=μ1，则χ=φ1＞0。当φ1≡0时，恒有ω1≡0，矛盾。则φ1不恒为0。因此

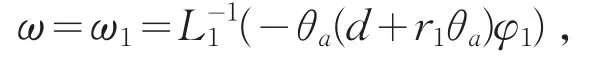
其中L1=d1∇2+（a-2θa）。则

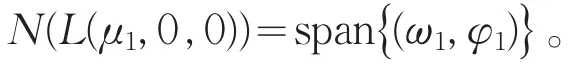
设（h1，h2）∈R（L（μ1，0，0），则必存在一组（ω，χ）∈X是下列方程的解：

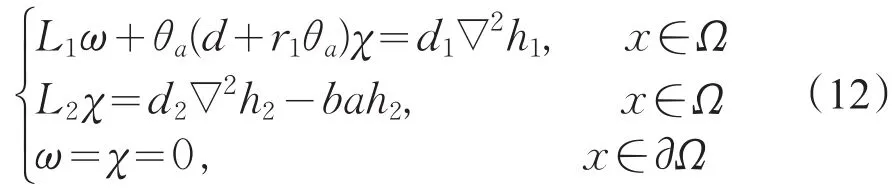
其中L2=d2∇2+（μ1-bθa）。对式（12）第二个方程两边同乘φ1在Ω上积分，并使用Green公式，结合式（9）知，当且仅当∫Ω（bθa-μ1-ba）φ1h2dx=0时，χ是第二个方程的解。又因为L1是可逆的，从而对于确定的χ，式（12）的第一个方程存在唯一的解ω。故可知

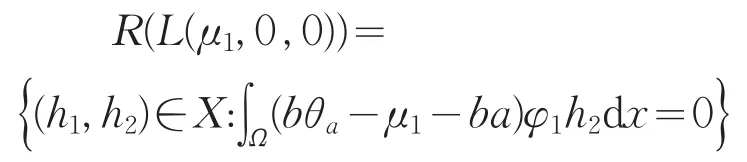
从而codimR（L（μ1，0，0）=1。

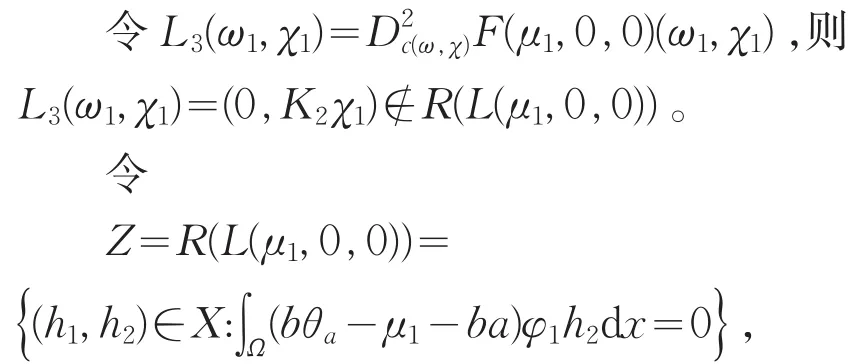
由局部分歧定理［10］知，存在δ＞0以及C1函数

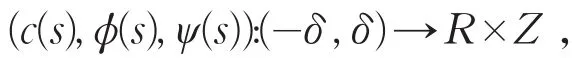
使得c（0）=μ1，ϕ（0）=0，ψ（0）=0，并且

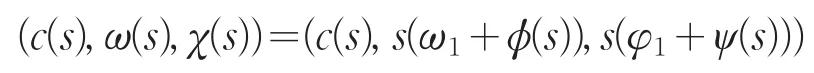
满足方程

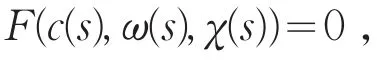
其中X=Z⊕N（L（μ1，0，0）。因此

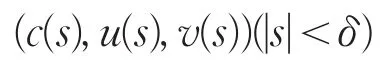
是系统（2）的分歧解，其中u（s）=θa-s（ω1+ϕ（s），v（s）=s（φ1+ψ（s）。若取0＜s＜δ，则其恰好为系统（2）的正解，且在分歧点（μ1，θa，0）附近，系统（2）的非负非平凡解要么在分支｛（c，θa，0）:c∈R+｝上，要么在分支｛（c（s），u（s），v（s）:0＜s＜δ｝上。

下面讨论分歧解的稳定性。

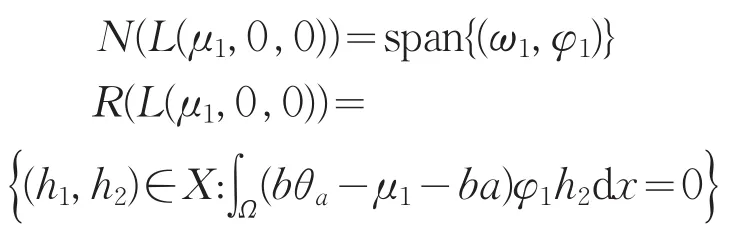
显然i（ω1，φ1）∉R（L（μ1，0，0），所以0是L（μ1，0，0）的一个i-单重特征值。

引理2 0是L（μ1，0，0）实部最大特征值，且L（μ1，0，0）所有其他特征值位于左复半平面。

证明：设μ0是L（μ1，0，0）的实部大于0的特征值，相应的特征函数为（ϕ1，ϕ2），则

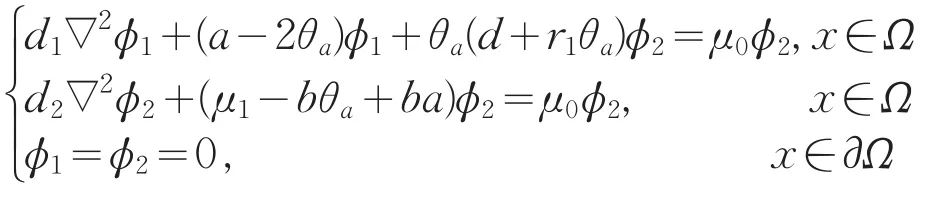
若ϕ2≡0，则（L1-μ0）ϕ1=0，从而ϕ1≡0，矛盾。因此ϕ2不恒为0。即μ0是d2∇2+（μ1-bθa+ba）的特征值，所以μ0∈R，从而μ0＞0。与

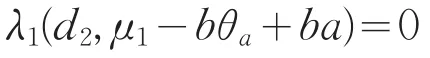
矛盾，故结论成立。

引理3存在分别定义在μ1和0邻域内的函数为c→（γ（c），U（c）∈R×X1，s→（η（s），V（S）∈R×X1，使得（γ（μ1），U（μ1）=（0，ω1，φ1）=（η（0），V（0），并且

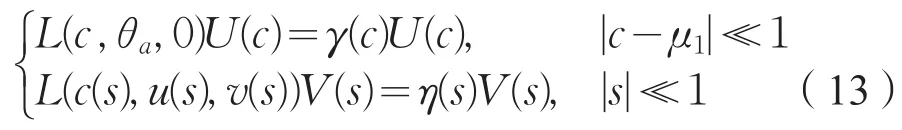
其中U（c）=（ϕ1（c），ϕ2（c），V（s）=（ψ1（s），ψ2（s），并且γ′（μ1）≠0，又若η（s）≠0（|s|≪1），则

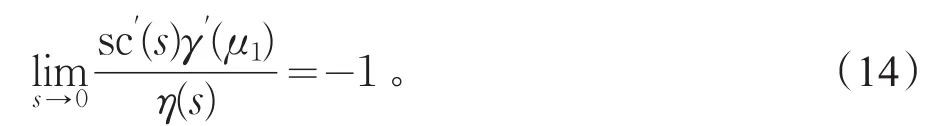
引理4γ′（μ1）＞0，其中γ（c）由式（13）式给出。

证明：由式（13）的第一个方程得，对于

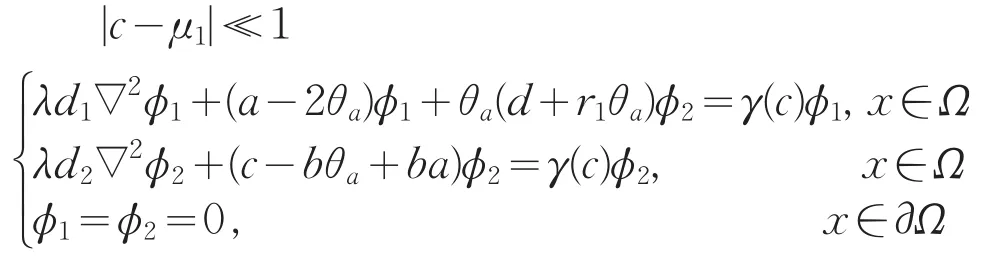
因为|c-μ1|≪1，那么当c充分接近μ1时，γ（c）|≪1。若ϕ2≡0，|c-μ1|≪1，则ϕ1≡0，矛盾。故ϕ2不恒为0。即γ（c）是d2∇2+（c-bθa+ba）的特征值。考虑到ϕ1＞0，因此只要|c-μ1|≪1，则ϕ1=ϕ1（c）＞0。所以γ（c）是d2∇2+（c-bθa+ba）的主特征值，且γ（c）关于c是递增的。又因γ′（μ1）≠0，所以γ′（μ1）＞0。

证明：将分歧解

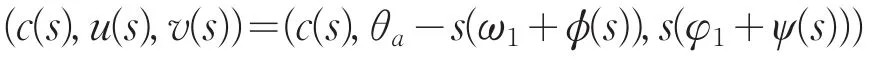
代入系统（2）的第二个方程，两端同除以s，再关于s在s=0处微分得

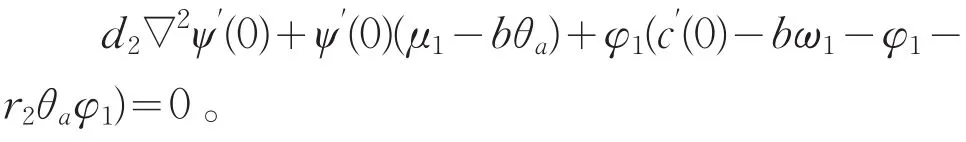
在上述方程两端同乘φ1在Ω上积分，并使用Green公式得

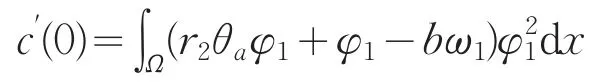
则c′（0）与I=∫Ω（r2θaφ1+φ1-bω1）φ12dx同号。则当I＞0时，c′（0）＞0，从而结论成立。

注：定理2表明，当r2充分大，即当化感作用充分大时，两物种可以到共存状态。

3　全局分歧

下面将定理1给出的局部分支延拓为全局分支。

定理3若ω1为方程（11）的解，则ω1＞0，x∈。

证明：由于ω1为方程（11）的解，故ω1满足

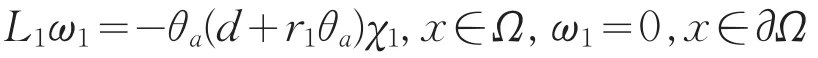
由文献［8］知L1的所有特征值全为负，从而存在函数φ＞0使得

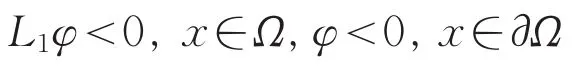
由广义最大值原理［11］可知ω1＞0。

定理4若a＞d1λ0，则由定理1给出的正分歧解最终与半平凡分支｛（c，0，θc）:c∈R+｝在c=处相接，其中由唯一确定。

证明:令G（c）（ω，χ）=D（ω，χ）T（c，0，0）（ω，χ），则

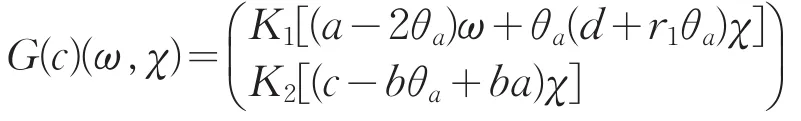
设λ≥1是G（c）的特征值，对应的特征函数为（ω，χ），且不恒为0，则

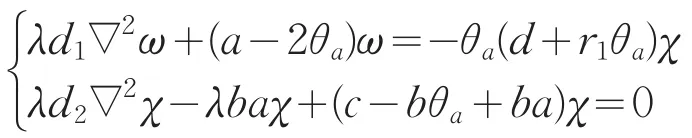
若χ≡0，则ω≡0，这与ω＞0矛盾，因此χ不恒为0。故存在i=1，2，…，使得c=ci（λ），其中ci（λ）是下列问题的特征值

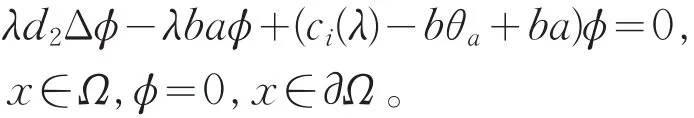
显然ci（λ）关于λ≥1是递增的，且满足

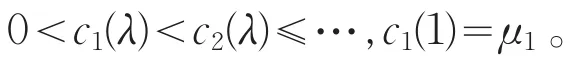
另一方面，若λ≥1，易知Lλ的所有特征值全为负，其中Lλ=λd1Δ+（a-2θa）。则

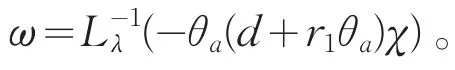
因此，λ≥1是G（c）的特征值，当且仅当c=ci（λ），i=1，2，…。

假设c＜μ1，则对任意的λ≥1，i≥1有c＜c1（1）＜ci（λ）。因此G（c）没有大于或等于1的特征值。即当c＜μ1时，index（T（c，·），0，0）=1。

假设μ1＜c＜c2（1），则对任意的λ≥1，i≥2有 c＜ci（λ）。又因，c1（1）=μ1，且c1（λ）关于λ严格递增，则存在唯一的，使得c=c1（）。因此，N（I-G（c）=span｛（，）｝且dimN（I-G（c）=1。其中是下列问题的主特征函数

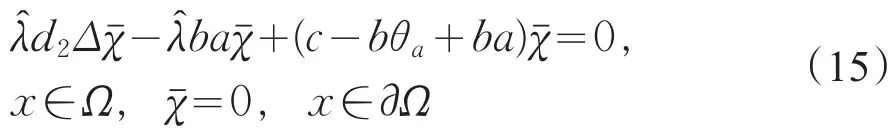
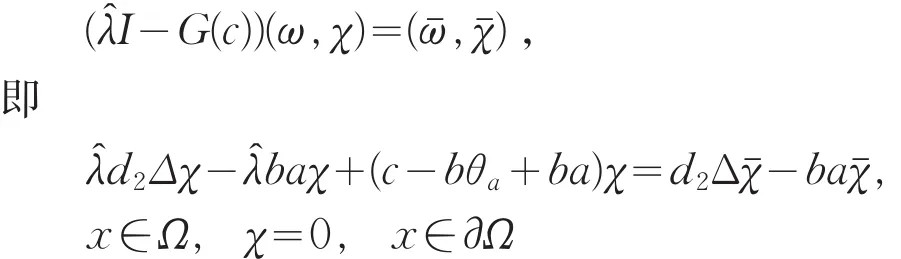
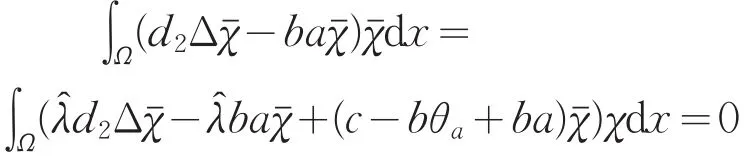
另一方面，由式（15）可得

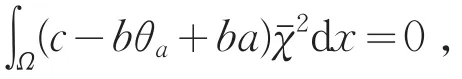
由引理1（Ⅰ）知，θa＜a，则c-bθa+ba恒大于0，矛盾。所以的重数是1。故当μ1＜c＜c2（1）时，index（T（c，·），0，0）=-1。

由全局分歧定理［12］知，在R+×X内，存在从（μ1，0，0）出发的连通分支S0，满足F（c，ω，χ）=0，且在（μ1，0，0）附近，F（c，ω，χ）=0的解都在由定理1给出的分歧曲线上。令

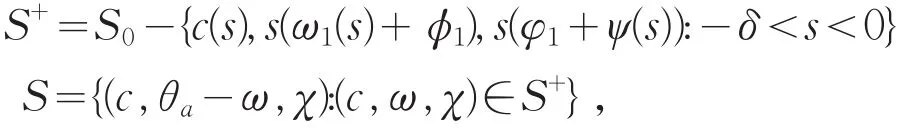
则S是系统（2）由（μ1，θa，0）发出的解曲线，且在（μ1，θa，0）附近仍然是正解。记

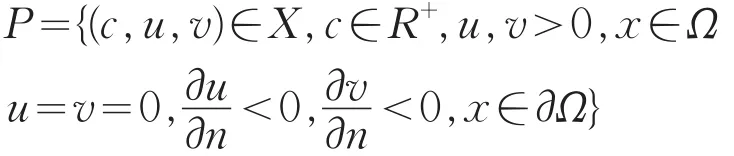
则在（μ1，θa，0）的邻域内有S⊂P，而且分支S-｛（μ1，θa，0）｝必满足下列条件之一：

（Ⅰ）S连接分歧点（μ1，θa，0）和（，θa，0），其中μ1≠；

（Ⅱ）在R×X内由（μ1，θa，0）延伸到∞；

（Ⅲ）包含一个点（c，u，v）∈R×｛Z｛0｝，其中Z是L（μ1，0，0）的核空间的补空间。

假设S-｛（μ1，θa，0）｝⊂P，则（Ⅰ）显然不成立。

由引理1知，u＜θa，v＜θc且c有界，由LP估计和Sobolev嵌入定理得，存在一个常数M＞0，使得||u||，||v||，||c||≤M。则S是有界的，故（Ⅱ）不成立。

若（Ⅲ）成立，由于Z=R（L（μ1，0，0），有

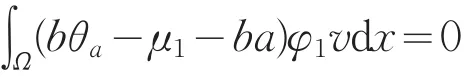
由引理1（Ⅰ）知，θa＜a，则bθa-μ1-ba在Ω上恒小于0，且v＞0，φ1＞0，矛盾。则（Ⅲ）不成立。

从而S-｛（μ1，θa，0）｝⊄P。即存在点

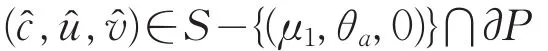
和序列

｛（cm，um，vm）｝⊂S⋂P，um＞0，vm＞0，x∈，使得当m→∞时，（cm，um，vm）→（，，）。因为（，，）∈∂P，故存在x0∈有≥0，（x0）=0，或≥0，（x0）=0。又因为满足

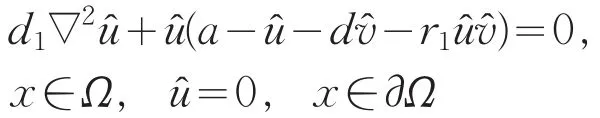
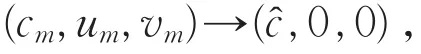
令Um=um/||um||，则Um满足

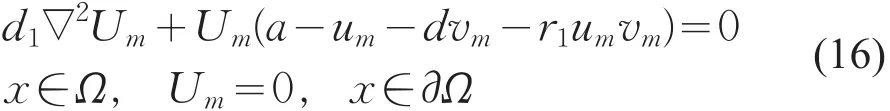
由LP估计和Sobolev嵌入定理知，存在Um的收敛子列（仍记为Um），使得当m→+∞时，Um→u在上成立，且u≥0（不恒为0）（x∈），在方程（16）中，令m→+∞得

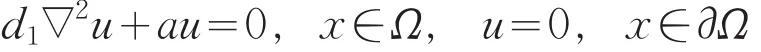
由强最大值原理可知:u＞0。从而有a=d1λ0，这与a＞d1λ0矛盾。

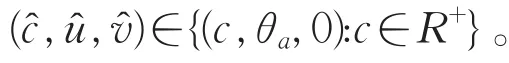
故当m→+∞时，序列（um，vm）→（θa，0），令

Vm=vm/||vm||，则Vm满足

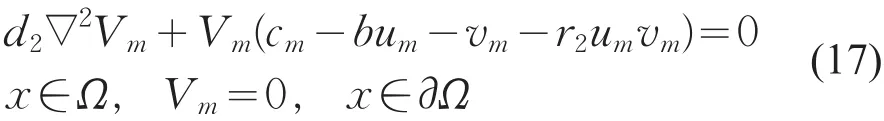
同理，由LP估计和Sobolev嵌入定理知，存在Vm的收敛子列（仍记为Vm），使得当m→+∞时，Vm→v在上成立，且v≥0（不恒为0）（x∈Ω¯），在方程（17）中，令m→+∞得

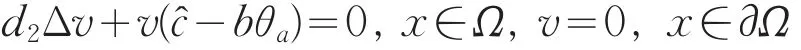
由于S与分支｛（c，0，θc）:c＞d2λ0｝在c=处相接，则为系统（2）的另一分歧点。故存在序列（m，um，vm），使得当m→+∞时，

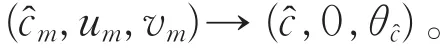
令Um=um/||um||，则Um满足

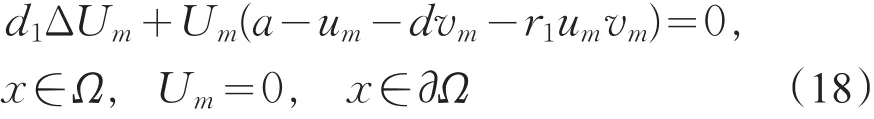
由LP估计和Sobolev嵌入定理知，存在Um的收敛子列（仍记为Um），使得当m→+∞时，Um→u在上成立。在式（18）中，令m→+∞得

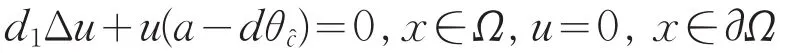
由强最大值原理可知：u＞0。有a=λ1（d1，dθ）。

4　结论

利用分歧理论研究了具有化感作用竞争模型正解的存在性。结果表明，系统（2）存在发自单重分歧点（μ1，θa，0）的局部分歧，且该分支可延拓为全局分支，最终交半平凡解分支｛（c，0，θc）:c∈R+｝于点（，0，θ）。从生态学角度看，如果两物种的化感作用满足一定条件时，两物种可以达到共存。

［1］RICE E L.Allelopathy［M］.New York:Academic Press，1984.

［2］CHATTOPHADYAY J.Effect of toxic substances on a two species competitive system［J］.Ecological Model，1996（84）: 287-289.

［3］ZHEN J，MA Z E.Periodic solution of a delay differential equations model of plankton allelopathy［J］.Computers and Mathematics withApplications，2002（44）:491-500.

［4］SAMANTA G P.A two-species competitive system under the influence of toxic substances［J］.Applied Mathematics and Computation，2010（216）:291-299.

［5］MUKHOPADHYAY M，CHATTOPADHYAY J，TAPASWI P K.A dalay differential equations model of plankton allelopathy［J］.Mathematical Bioscience，1998（149）:167-189.

［6］TIAN C R，LIN Z G.Asymptotic behavior of solutions of a periodic diffusion system of plankton allelopathy［J］.NonlinearAnalysis，2010（11）:1581-1588.

［7］TIAN C R，XU F，LIU Y.Stable solution of a delay parabolic equation of plankton allelopathy［J］.Journal of Mathematical Research and Exposition，2005（4）:727-733.

［8］KEENER J.Principles of applied mathematics［M］.Boston: Addison-Wesley Publishing Company，1988.

［9］叶其孝，李正元，王明新，等.反应扩散方程引论［M］.北京:科学出版社，2011.

［10］SMOLLER J.Shock waves and reaction-diffusion equations［M］.New York:Springer，1984.

［11］WU J H.Global bifurcation of coexistence state for the competition model in the chemostat［J］.Nonlinear Analysis，2000

（39）:817-835.

［12］BLAT J，BROWN K J.Global bifurcation of positive solutions in some systems of elliptic equations［J］.SIAM Journal on MathematicalAnalysis，1986（17）：1339-1353.

QualitativeAnalysis of Competition Model withAllelopathy

WANG Huan，WANG Yan'e
（College of Mathematics and Information Science，Shaanxi Normal University，Xi'an 710062，Shaanxi，China）

The competition model of allelopathy with Dirichlet boundary is studied.The local bifurcation branch of positive solutions is constructed by the local bifurcation theory.Moreover，the local bifurcation branch can be extended to a global solution branch by using the global bifurcation theory. The results show that the global solution branch connects with two semi-trivial solution branches of the model.From a biological point of view，two competitors can coexist when the allelopathic factors satisfy some conditions.

allelopathy；bifurcation theory；competition model

O175.26

A

1672-2914（2015）06-0036-05

2015-05-15

王欢（1990-），女，陕西咸阳市人，陕西师范大学数学与信息科学学院硕士研究生，研究方向为反应扩散方程及其应用。

王艳娥，讲师，Email:wye@snnu.edu.cn。