一类特殊矩阵特征向量的求法

王欣欣

(南通理工学院 基础教学学院，江苏 南通 226000)

物理、力学和工程技术中的许多问题在数学上都归结为求矩阵的特征值与特征向量.求二阶矩阵的特征向量很容易，但从不同的视角去剖析其由来，体现了数学赋予人们多维度的思维方式.本文对一类特殊的二阶矩阵进行研究，根据其特殊性构造出相应的特征向量，相比传统的方法更加简便快捷.

1 相关定理

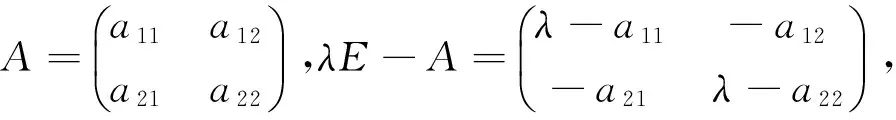
(1)若λ1≠λ2，由于特征向量为非零向量，故可以分以下四种情况：

A为对应于特征值λ1的一个特征向量：

① 若λ1≠a11，或a12≠0,则A对应于特征值λ1的一个特征向量为

(1)

② 若λ1≠a22，或a21≠0，则A对应于特征值λ1的一个特征向量为

(2)

A为对应于特征值λ2的一个特征向量：

③ 若λ2≠a11，或a12≠0，则A对应于特征值λ2的一个特征向量为

(3)

④ 若λ2≠a22，或a21≠0，则A对应于特征值λ2的一个特征向量为

(4)

(2)若λ1=λ2，且R(λ1E-A)=1时，由于特征向量为非零向量，故可以分为以下两种情况：

① 若λ1=λ2≠a11，或a12≠0，则A对应于特征值λ1、λ2的一个特征向量为

(5)

② 若λ1=λ2≠a22，或a21≠0，则A对应于特征值λ1、λ2的一个特征向量为

(6)

注：如果(1)中的①、②同时满足，则任选其一作为相应的特征向量即可，其结果是相同的.

同理可以应用于(2)中的两种情况.

以下给出(1)中①的证明.

证明特征多项式

(7)

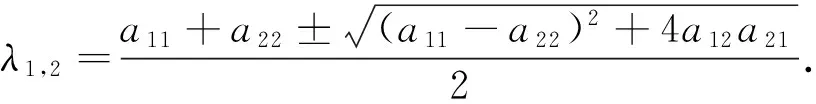
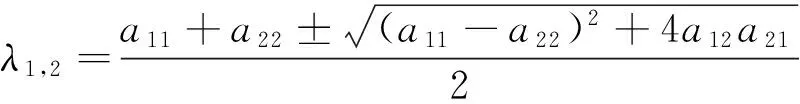
(8)

现验证其正确性，即证明Aξ1=λ1ξ1.

则Aξ1=λ1ξ1成立.得证.

对于(1)中的 ②、③、④，以及(2)，证明方法相同，不再赘述.

2 例题

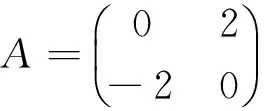
解A的特征多项式为

所以A的特征值为λ1=2i,λ2=-2i.

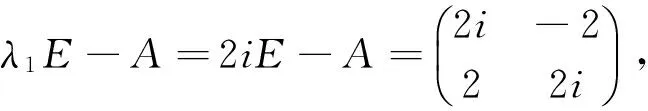
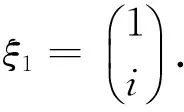
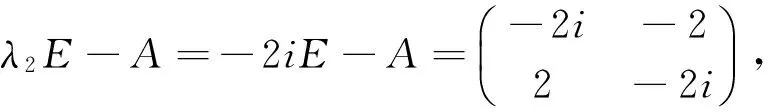
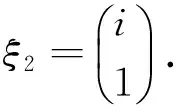
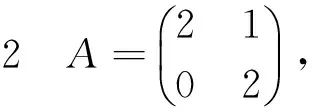
解A的特征多项式为

所以A的特征值为λ1=λ2=2.

所以kξ(k≠0)是对应于λ1=λ2=2的全部特征向量.

参考文献：

[1] 夏学文.线性代数[M].湖南：中南大学出版社，2014：116-117.

[2] 李林曙，施光燕.线性代数[M].北京：中国人民大学出版社，2002：223-224.