C3型李代数的张量积分解

2022-03-29代佳华王利萍盛昱杰李泽妤

北京建筑大学学报 2022年1期

代佳华，王利萍，盛昱杰，李泽妤

(1.北京建筑大学理学院，北京 100044; 2.北京工商大学嘉华学院，北京 101118)

1979年,KAZHDAN等[1]提出了Kazhdan-Lusztig理论, 并且指出Kazhdan-Lusztig系数是该理论的核心研究对象。在计算最低双边胞腔上的Kazhdan-Lu-sztig系数时, 通常需要求出对应李代数中的张量积分解。许超[2]给出了A2型李代数不可约模的张量积分解的计算方法。于桂海等[3]给出了特征数大于0的代数闭域上C2型单连通半单代数群，限制支配权所对应的不可约模的张量积分解。魏玉丽等[4]计算出了A3型李代数的部分张量积分解。

1 预备知识

1.1 C3型单李代数

W0={e,1,2,3,12,13,21,23,32,121,123,132,213,
232,321,323,1213,1232,1321,1323,2132,2321,
2323,3213,12132,12321,12323,13213,21321,
21323,23213,32132,121321,121323,123213,
132132,213213,232132,321323,1231213,
1232132,1321323,2132132,2321323,
12132132,12321323,21321323,121321323}

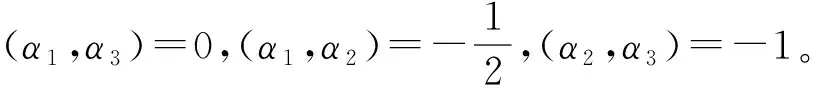
并且Λ=x1+x2+x3,Λ+=x1+x2+x3,Λr=α1+α2+α3。

在Λ中, 存在序关系λ≤μ, 即μ-λ可以写成关于α1,α2,α3的非负线性组合。

1.2 李代数中张量积分解的结论

引理2如果λ∈Λ+，则以λ为首权的不可约L-模V=V(λ)是有限维的，且权集合∏(λ)被W0所置换，使得对于σ∈W0，有dimVμ=dimVσμ。

引理3(Freudenthal公式) 设V=V(λ)是首权为λ(λ∈Λ+)的不可约L-模，如果μ∈Λ,则μ在V内的重数m(μ)可从如下的递推得到：

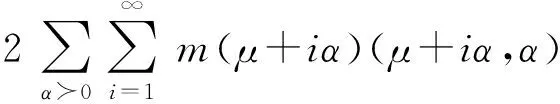
(1)

引理4使得V(λ)可能出现在V(λ′)⊗V(λ″)的加项中的λ∈Λ+,只能形如μ+λ″,μ∈∏(λ′)。当这样的μ+λ″都是支配权时，V(μ+λ″)出现在张量积内，且重数为mλ′,λ″μ+λ″=mλ′(μ)。

2 C3型李代数的张量积分解

根据李代数的知识, 给出了共轭元以及权重数的算法:

第一步,给定任意1个首权λ。用W0中的48个元素去作用λ，从而得到共轭元,定义为S(λ)(λ∈Λ+)。此处:

λ=aα1+bα2+cα3

(2)

式中：a,b,c均为实数。

第二步，找到所有比λ低的支配权μ:

μ=aiα1+biα2+ciα3

(3)

式中:ai,bi,ci均为实数, 且满足

用第一步的方法得到μ的共轭元集S(μ)(μ∈Λ+)。

第四步，首权λ的重数为1。

表1 层

第五步，在算某个支配权的重数时,按照水平高度表，然后利用Freudenthal公式即可得到该支配权的重数。

2.1 ∏(λ)以及权重数m(μ)的部分计算结果

通过编程可以得到:

S(x1)={x1,-x1,x2-x1,x1-x2,x3-x2,x2-x3}
S(x2)={x2,-x2,x2-x1-x3,x1-x2+x3,x3-
x1,x1-x3,x1+x2-x3,-x1-x2+x3，
-x1+2x2-x3,x1-2x2+x3,2x1-x2,x2-2x1}
S(x3)={x3,-x3,2x2-x3,x3-2x2,x3-2x1,
2x1-x3，-2x1+2x2-x3,2x1-2x2+x3}
S(2x1)={2x1,-2x1,2x2-2x1,2x1-2x2,2x3-
2x2,2x2-2x3}
S(2x2)={2x2,-2x2,2x2-2x1-2x3,
2x1-2x2+2x3,2x3-2x1,
2x1-2x3,2x1+2x2-2x3,-2x1-2x2+2x3，
-2x1+4x2-2x3,2x1-4x2+2x3,4x1-2x2,2x2-4x1}
S(2x3)={2x3,-2x3,4x2-2x3,2x3-4x2,2x3-4x1,
4x1-2x3，-4x1+4x2-2x3,4x1-4x2+2x3}
S(x1+x2)={x1+x2,-x1-x2,2x2-x1,x1-2x2,
2x1-x2+x3,-2x1+x2-x3-2x1+x2+x3,
2x1-x2-x3,x1-2x2+2x3,-x1+2x2-2x3,
2x1+x2-x3,-2x1-x2+x3,3x1-x2,x2-3x1,
x1+2x2-2x3,-2x1+3x2-x3,2x1-3x2+x3,
-3x1+2x2,3x1-2x2,-x1+3x2-2x3}
S(x1+x3)={x1+x3,-x1-x3,x3+x2-x1,
x1-x2-x3,-x1-2x2+x3-x1+3x2-x3,
x1-3x2+x3,-x2+2x3,x2-2x3,3x1-2x2+x3,
-3x1+2x2-x3,-3x1+x2+x3,3x1-x2-x3,
3x2-2x3,2x3-3x2,2x1-3x2+2x3,-2x1+3x2-2x3,
-3x1+x3,3x1-x3,-3x1+3x2-x3,
3x1-3x2+x3,-2x1-x2+2x3,2x1+x2-2x3}
S(x2+x3)={x2+x3,-x2-x3,x1-x2+2x3,
-x1+x2-2x3,-3x2+2x3-x1,x1-2x3,3x1-2x3,
2x3-3x1,3x1-3x2+2x3,-3x1+3x2-2x3,
x1+3x2-2x3,-x1-3x2+2x3,x1-4x2+2x3,
-x1+4x2-2x3,-4x1+3x2-x3,4x1-3x2+x3,
-3x1-x2+2x3,3x1+x2-2x3,-4x1+x2+x3,
4x1-x2-x3,-3x1+4x2-2x3,3x1-4x2+2x3}
∏(x1)={x1,-x1,x2-x1,x1-x2,x3-x2,x2-x3}
∏(x2)={x2,-x2,x2-x1-x3,x1-x2+x3,
x3-x1,x1-x3,x1+x2-x3,-x1-x2+x3，
-x1+2x2-x3,x1-2x2+x3,
2x1-x2,x2-2x1,0}
∏(x3)={x3,-x3,2x2-x3,x3-2x2,x3-2x1,
2x1-x3，-2x1+2x2-x3,2x1-2x2+x3}
∏(2x1)={2x1,-2x1,2x2-2x1,2x1-2x2,
2x2-2x3,2x3-2x2,x1-x3,x1+x2-x3,
-x1-x2+x3，-x1+2x2-x3,
x1-2x2+x3,2x1-x2,x2-2x1,0}
∏(2x2)={2x2,-2x2,2x1-2x2+2x3,
-2x1+2x2-2x3,2x3-2x1,2x1-2x3,
2x1+2x2-2x3,-2x1-2x2+2x3,2x1-4x2+2x3,
-2x1+4x2-2x3,4x1-2x2,2x2-4x1,x1+x3,
-x1-x3,x3+x2-x1,x1-x2-x3,x1+2x2-x3,
-x1-2x2+x3-x1+3x2-x3,x1-3x2+x3,-x2+2x3,
x2-2x3,3x1-2x2+x3,-3x1+2x2-x3,-3x1+x2+x3,
3x1-x2-x3,3x2-2x3,2x3-3x2,2x1-3x2+2x3,
-2x1+3x2-2x3,-3x1+x3,3x1-x3,
-3x1+3x2-x3,3x1-3x2+x3,-2x1-x2+2x3,
2x1+x2-2x3,2x1,-2x1,2x2-2x1,2x1-2x2,
2x2-2x3,2x3-2x2,x2,-x2,x1-x2+x3,
-x1+x2-x3,x3-x1,x1-x3,x1+x2-x3,
-x1-x2+x3,-x1+2x2-x3,x1-2x2+x3,
2x1-x2,x2-2x1,0}
∏(2x3)={2x3,-2x3,4x2-2x3,2x3-4x2,
4x1-4x2+2x3,-4x1+4x2-2x3,2x3-4x12x2,
-2x2,2x1-2x2+2x3,-2x1+2x2-2x3,2x3-2x1,
2x1+2x2-2x3,-2x1-2x2+2x3,2x1-4x2+2x3,
4x1-2x2,2x2-4x1,x1+x3,-x1-x3,x3+x2-x1,
x1-x2-x3,-x1-2x2+x3-x1+3x2-x3,
x1-3x2+x3,-x2+2x3,x2-2x3,-3x1+2x2-x3,
-3x1+x2+x3,3x1-x2-x3,3x2-2x3,
2x3-3x2,2x1-3x2+2x3,-2x1+3x2-2x3,
-3x1+x3,3x1-x3,3x1-3x2+x3,-2x1-x2+2x3,
2x1+x2-2x3,2x1,-2x1,2x2-2x1,2x2-2x3,2x3-2x2,
x2,-x2,x1-x2+x3,-x1+x2-x3,x3-x1,
x1+x2-x3,-x1-x2+x3,-x1+2x2-x3,
x1-2x2+x3,2x1-x2,0}
∏(x1+x3)={x1+x3,-x1-x3,x3+x2-x1,
x1-x2-x3,x1+2x2-x3,-x1-2x2+x3,
-x1+3x2-x3,x1-3x2+x3,-x2+2x3,x2-2x3,
3x1-2x2+x3,-3x1+2x2-x3,-3x1+x2+x3,
3x1-x2-x3,3x2-2x3,2x3-3x2,2x1-3x2+2x3,
-2x1+3x2-2x3,-3x1+x3,3x1-x3,-3x1+3x2-x3,
3x1-3x2+x3,-2x1-x2+2x3,2x1+x2-2x3,
2x1,-2x1,2x2-2x1,2x2-2x3,2x3-2x2,x2,
-x2,x1-x2+x3,-x1+x2-x3,x3-x1,x1-x3,
-x1-x2+x3,-x1+2x2-x3,x1-2x2+x3,
2x1-x2,x2-2x1,0}
∏(x1+x2)={x1+x2,-x1-x2,2x2-x1,
x1-2x2,2x1-x2+x3,-2x1+x2-x3-2x1+x2+x3,
2x1-x2-x3,-3x1+2x2,-x1+2x2-2x3,
2x1+x2-x3,-2x1-x2+x3,3x1-x2,x1+2x2-2x3,
-2x1+3x2-x3,2x1-3x2+x3,3x1-2x2,
-x1+3x2-2x3,x1-3x2+2x3,x1,-x1,x3-x2,
x1-x2,x2-x1x3,-x3,2x2-x3,x3-2x2,
2x1-2x2+x3,-2x1+2x2-x3,2x1-x3,x3-2x1}
∏(x2+x3)={x2+x3,-x2-x3,x1-x2+2x3,
-x1+x2-2x3,3x2-x3,x1-2x3,3x1-3x2+2x3,
-3x1+3x2-2x3,2x3-3x1,3x1-2x3,-x1-3x2+2x3,
-x1+4x2-2x3,x1-4x2+2x3,4x1-3x2+x3,
3x1+x2-2x3,-3x1-x2+2x3,-4x1+x2+x3,
4x1-x2-x3,3x1-4x2+2x3x1+x2,-x1-x2,
2x2-x1,x1-2x2,2x1-x2+x3,-2x1+x2+x3,
2x1-x2-x3,x1-2x2+2x3,-x1+2x2-2x3,
2x1+x2-x3,-2x1-x2+x3,3x1-x2,
x2-3x1，-2x1+3x2-x3,2x1-3x2+x3,
-3x1+2x2,3x1-2x2,x1-3x2+2x3,x1,-x1,
x3-x2,x2-x3,x1-x2,x2-x1,x3,-x3,
2x2-x3,x3-2x2,2x1-2x2+x3,-2x1+2x2-x3}

由引理2和引理3得到关于重数的命题：

命题1设V=V(2x1)是首权为2x1的不可约L-模，则μ∈∏(2x1)时, 有:

证明: 首权λ=2x1=2α1+2α2+α3,比其低的支配权有x2=α1+2α2+α3和0。

从而∏(2x1)=S(2x1)∪S(x2)∪S(0)。∏(2x1)中的权按照水平排列, 见表2。

表2 重数

2x3-2x2和2x2-2x1是2x1的共轭元, 由引理2得出两者的重数均为1。然后计算m(x2)。

由引理1得到,δ=3α1+5α2+3α3。由内积的关系式得到:(2x1+δ,2x1+δ)=15, (x2+δ,x2+δ)=13, (2x1,α1)=1。

由Freudenthal公式得出m(x2)=1，(δ,δ)=7，(2x3-2x2,α3)=2,(-x1+2x2-x3,α2)=1,(2x1-x2,α1)=1。

由Freudenthal公式得到m(0)=3。命题得证。

类似方法可以得到下面6个命题。

命题2设V=V(2x2)是首权为2x2的不可约L-模，则μ∈∏(2x2)时, 有：

命题3设V=V(λ)是首权为λ的不可约L-模，λ=x1,x2,x3。如果μ∈∏(λ), 则μ在V内的重数m(μ)=1。

命题4设V=V(2x3)是首权为2x3的不可约L-模，则μ∈∏(2x3)时, 有：

命题5设V=V(x1+x3)是首权为x1+x3的不可约L-模，则μ∈∏(x1+x3)时, 有：

命题6设V=V(x1+x2)是首权为x1+x2的不可约L-模，则μ∈∏(x1+x2)时, 有：

命题7设V=V(x2+x3)是首权为x2+x3的不可约L-模，则μ∈∏(x2+x3)时,有：

2.2 C3型李代数的张量积分解

定理1根据引理4, 得到以下结论：

第一, 当λ′∈{x1,x2,x3}时, 对任意λ″∈Λ+，有mλ′,λ″,μ+λ″=1。

第二,当λ′=2x1,λ″∈{2x1,2x2,2x3,x1+x2,x1+x3,x2+x3}时,mλ′,λ″,λ″=3, 其余重数为1。

第三,当λ′=2x2时,对任意λ″∈Λ+，有mλ′,λ″,λ″=6。当λ″=2x2时,mλ′,λ″,2x1+x2=mλ′,λ″,x1+x3=mλ′,λ″,x2=mλ′,λ″,3x2=mλ′,λ″,x1+x2+x3=3,mλ′,λ″,2x1=mλ′,λ″,2x3=2, 其余重数为1; 当λ″=2x3时,mλ′,λ″,2x3+x2=mλ′,λ″,x1+x3=3，mλ′,λ″,2x1+2x3=mλ′,λ″,x3+x2+x1=mλ′,λ″,2x3=mλ′,λ″,2x2=2,其余重数为1;当λ″=x1+x2时,mλ′,λ″,2x1+x2=3,mλ′,λ″,x1+2x2=mλ′,λ″,2x1+x3=mλ′,λ″,x3=mλ′,λ″,3x1=mλ′,λ″,x2+x3=2，其余重数为1;当λ″=x1+x3时,mλ′,λ″,x1+x2+x3=mλ′,λ″,2x3=mλ′,λ″,2x2=3,mλ′,λ″,3x1+x3=mλ′,λ″,2x1+x2=2,其余重数为1;当λ″=x2+x3时,mλ′,λ″,x1+2x3=mλ′,λ″,2x1+x3=mλ′,λ″,x3=mλ′,λ″,3x1=mλ′,λ″,2x2+x3=3,mλ′,λ″,x1+2x2=mλ′,λ″,2x1+x2+x3=2,其余重数为1。

第四, 当λ′=2x3时，对任意λ″∈Λ+，有mλ′,λ″,λ″=4。当λ″=2x3时,mλ′,λ″,2x1+2x3=mλ′,λ″,x1+2x3=mλ′,λ″,2x2=mλ′,λ″,x1+x3=3,其余重数为1; 当λ″=x1+x2时,mλ′,λ″,2x1+x2=3,mλ′,λ″,x1+2x2=mλ′,λ″,2x1+x3=mλ′,λ″,x3=mλ′,λ″,3x1=mλ′,λ″,x2+x3=3,其余重数为1。

第五,当λ′=x1+x3,λ″=x1+x3时，mλ′,λ″,x1+x2+x3=mλ′,λ″,x2=mλ′,λ″,2x1=mλ′,λ″,2x2=mλ′,λ″,2x1+x2=3,mλ′,λ″,x1+x3=4, 其余重数为1。

第六, 当λ′=x1+x2，λ″=x1+x2时,mλ′,λ″,2x1+x2+x3=mλ′,λ″,2x2=mλ′,λ″,x2=mλ′,λ″,2x1=mλ′,λ″,x1+x3=3,mλ′,λ″,x1+x2+x3=2, 其余重数为1。当λ″=x1+x3时,mλ′,λ″,x1=mλ′,λ″,3x1=2,mλ′,λ″,x2+x3=mλ′,λ″,x3=mλ′,λ″,x2+x3=mλ′,λ″,2x1+x3=3, 其余重数为1。

第七,当λ′=x2+x3，λ″={x2+x3,x1+x3}时,mλ′,λ″,x3+λ″=mλ′,λ″,-x3+λ″=mλ′,λ″,2x2-x3+λ″=mλ′,λ″,2x1-x3+λ″=3mλ′,λ″,x3+x2+λ″=5, 其余为重数为1。

V(x1)⊗V(x1)=V(2x1)⊕V(x2)⊕V(0)；
V(x1)⊗V(x2)=V(x1+x2)⊕V(x3)⊕V(x1)；
V(x1)⊗V(x3)=V(x1+x3)⊕V(x2)；
V(x1)⊗V(2x1)=V(3x1)⊕V(x1+x2)⊕V(x1)；
V(x1)⊗V(2x2)=V(x1+2x2)⊕V(x2+x3)⊕
V(x1+x2)；
V(x1)⊗V(2x3)=V(x1+2x3)⊕V(x2+x3)；
V(x1)⊗V(x1+x2)=V(2x1+x2)⊕V(2x2)⊕
V(x1+x3)⊕V(2x1)⊕V(x2)；
V(x1)⊗V(x1+x3)=V(2x1+x3)⊕V(x1+x2)⊕
V(x2+x3)⊕V(x3)；
V(x1)⊗V(x2+x3)=V(x1+x2+x3)⊕V(2x2)⊕
V(2x3)⊕V(x1+x3)；
V(x2)⊗V(x2)=V(2x2)⊕V(x1+x3)⊕V(0)⊕
V(2x1)；
V(x2)⊗V(x3)=V(x1+x2)⊕V(x2+x3)⊕V(x1)；
V(x2)⊗V(2x1)=V(2x1+x2)⊕V(x1+x3)⊕
V(2x2)⊕V(2x1)；
V(x3)⊗V(x3)=V(2x3)⊕V(2x1)⊕V(0)⊕V(2x2)；
V(x2)⊗V(2x2)=V(3x2)⊕V(x1+x2+x3)⊕
V(x1+x3)⊕V(2x1+x2)⊕V(x2)⊕V(2x2)；
V(x2)⊗V(2x3)=V(x2+2x3)⊕V(x1+x2+x3)⊕
V(x1+x3)⊕V(2x3)；
V(x2)⊗V(x1+x2)=V(x1+2x2)⊕V(2x1+x3)⊕
V(x2+x3)⊕V(3x1)⊕V(x1)⊕V(x3)V(x1+x2)；
V(x2)⊗V(x2+x3)=V(x3+2x2)⊕V(x1+2x3)⊕
V(x1+2x2)⊕V(2x1+x3)⊕V(x1+x2)⊕V(x3)⊕
V(x2+x3)；
V(x2)⊗V(x1+x3)=V(x1+x2+x3)⊕V(2x3)⊕
V(2x1+x2)⊕V(2x2)⊕V(2x1)⊕V(x2)⊕
V(x1+x3)；
V(x3)⊗V(2x1)=V(x3+2x1)⊕V(x3)；
V(x3)⊗V(2x2)=V(2x2+x3)⊕V(2x1+x3)⊕
V(x3)；
V(x3)⊗V(2x3)=V(3x3)⊕V(2x2+x3)⊕
V(2x1+x3)⊕V(x3)；
V(2x1)⊗V(2x1)=V(4x1)⊕V(2x1+x2)⊕
V(2x2)⊕V(x1+x3)⊕3V(2x1)⊕V(x2)⊕V(0)；
V(x3)⊗V(x1+x3)=V(2x3+x1)⊕V(x1)⊕
V(3x1)⊕V(x1+2x2)；
V(x3)⊗V(x2+x3)=V(2x3+x2)⊕V(x2)⊕
V(3x2)⊕V(2x1+x2)；
V(2x1)⊗V(2x2)=V(2x1+2x2)⊕V(3x2)⊕
V(x1+x2+x3)⊕V(2x3)⊕V(2x1+x2)⊕
3V(2x2)⊕V(x2)⊕V(x1+x3)⊕V(2x1)；
V(2x1)⊗V(2x3)=V(2x1+2x3)⊕V(x1+x2+x3)⊕
V(x2+2x3)⊕3V(2x3)⊕V(2x2)⊕V(x1+x3)；
V(2x1)⊗V(x1+x2)=V(3x1+x2)⊕3V(x1+x2)⊕
V(2x1+x3)⊕V(x3)⊕V(x1)⊕3V(x1)⊕
V(x2+x3)⊕V(x1+2x2)；
V(2x1)⊗V(x1+x3)=V(3x1+x3)⊕
V(x1+x2+x3)⊕V(2x3)⊕V(2x1+x2)⊕
V(2x2)⊕3V(x1+x3)⊕V(2x1)⊕V(x2)；
V(2x1)⊗V(x2+x3)=V(x1+2x2)⊕
V(2x1+x2+x3)⊕V(x3)⊕V(x1+x2)⊕
V(2x2+x3)⊕V(x1+2x3)⊕V(2x1+x3)⊕
3V(x2+x3)；
V(2x2)⊗V(x1+x2)=
V(x1+3x2)⊕V(2x1+x2+x3)⊕
V(2x2+x3)⊕V(x1+2x3)⊕2V(3x1+x2)⊕
3V(x1+2x2)⊕3V(2x1+x3)⊕3V(x2+x3)⊕
3V(3x1)⊕6V(x1+x2)⊕3V(x3)⊕3V(x1)；
V(2x2)⊗V(2x3)=V(3x2)⊕V(x1+3x3)⊕
V(2x2+2x3)⊕V(2x1+2x2)⊕
2V(2x1+2x3)⊕3V(x2+2x3)⊕V(3x1+x3)⊕
V(x1+2x2+x3)⊕2V(x1+x2+x3)⊕2V(2x3)⊕
6V(2x3)⊕2V(2x2)⊕3V(x1+x3)⊕V(2x1)⊕V(x2)；
V(2x2)⊗V(x2+x3)=V(3x2+x3)⊕
V(x1+x2+2x3)⊕V(x1+3x2)⊕

6V(x2+x3)⊕2V(2x1+x2+x3)⊕3V(2x2+x3)⊕
V(3x1+x2)⊕V(x1)⊕3V(x1+2x3)⊕
2V(x1+2x2)⊕3V(2x1+x3)⊕V(3x3)⊕
V(3x1)⊕3V(x1+x2)⊕3V(x3)；
V(2x2)⊗V(x1+x3)=V(x1+2x2+x3)⊕
V(x2+2x3)⊕V(2x1+2x2)⊕
V(3x2)⊕V(3x2)⊕2V(3x1+x3)⊕V(4x1)⊕
3V(2x3)⊕V(0)⊕2V(2x1+x2)⊕3V(2x2)⊕
6V(x1+x3)⊕3V(2x2)；
V(2x3)⊗V(2x3)=V(4x3)⊕V(2x2+2x3)⊕
V(x1+3x3)⊕V(4x2)⊕V(2x1)⊕V(x2)⊕
V(x1+2x2+x3)⊕2V(2x1+2x3)⊕
V(2x1+2x2)⊕2V(x1+2x3)⊕V(3x1+x3)⊕
V(3x2)⊕2V(x1+x2+x3)⊕V(4x1)⊕4V(2x3)⊕
V(2x1+x2)⊕2V(2x2)⊕2V(x1+x3)；
V(2x3)⊗V(x1+x2)=V(x1+3x2)⊕
V(x1+x2+2x3)⊕V(x1+2x3)⊕
2V(2x1+x3)⊕V(2x1+x2+x3)⊕V(2x2+x3)⊕
2V(3x1+x2)⊕2V(x1+2x2)⊕2V(x2+x3)⊕
2V(3x1)⊕4V(x1+x2)⊕2V(x3)⊕V(x1)；
V(2x3)⊗V(x1+x3)=V(x1+3x3)⊕
V(x1+2x2+x3)⊕V(2x1+2x3)⊕
V(x2+2x3)⊕V(2x1+2x2)⊕V(3x2)⊕V(0)⊕
2V(3x1+x3)⊕V(4x1)⊕2V(2x3)⊕2V(2x1+x2)⊕
2V(2x2)⊕4V(x1+x3)⊕2V(2x1)⊕2V(x2)；
V(x1+x2)⊗V(x1+x3)=V(2x1+x2+x3)⊕
V(2x2+x3)⊕V(3x1+x2)⊕2V(x1+2x3)⊕
V(2x2+x1)⊕3V(2x1+x3)⊕3V(x2+x3)⊕
2V(3x1)⊕3V(x1+x2)⊕3V(x3)⊕
2V(x1)⊕V(2x2+x3)；
V(x1+x3)⊗V(x1+x3)=V(2x1+2x3)⊕
V(0)⊕V(x2+2x3)⊕V(3x2)⊕
V(4x1)⊕V(2x1+2x2)⊕V(3x1+x3)⊕
3V(x3+x2+x1)⊕3V(x2)⊕3V(2x2)⊕3V(2x1)⊕
3V(2x1+x2)⊕4V(x1+x3).