无理性幂级数理论起源和发展

王全来

（天津师范大学计算机与信息工程学院，天津300387）

［科技史与科技传播研究］

无理性幂级数理论起源和发展

王全来

（天津师范大学计算机与信息工程学院，天津300387）

利用历史分析和比较的方法，探讨无理性幂级数理论的发展脉络；纽曼第一个提出了“无理性幂级数”的名称；在纽曼工作的影响下，莫德尔、施瓦兹等人对此做出了重要贡献。F W Carroll和J H B Kemperman等人把无理性幂级数的研究纳入到不可开拓幂级数理论研究中，推广了前人的有关结果。

无理性幂级数；解析开拓；外尔均匀分布；有理函数

构造某类幂级数在单位圆之外不可开拓问题是幂级数理论研究中的重要内容。该问题较早由魏尔斯特拉斯研究，并引入了自然边界的概念。其后许多数学家如庞加莱、阿达玛、波莱尔等人进行了深入探讨，并构造了不同类型的例子，具体内容可参见文献［1］。

无理性幂级数作为数学家构造的在单位圆之外不可开拓的一类幂级数在1921年由赫克（E Hecke，1887—1947）引入，其他数学家如纽曼（M Newman，1897—1984）、莫德尔（L J Mordell，1888—1972）、施瓦兹（W Schwarz）等人进行研究，并得到了诸多深刻结果。无理性幂级数理论的进一步发展是由Caroll、Kemperman等人做出的。

1　无理性幂级数理论起源

赫克作为一位数论学家，在《论解析函数和模1数的分布》［2］（1921）中，依据数（nξ）模1均匀分布和外尔均匀分布定理，指出若α为无理数，则幂级数∑R（mα）xm和∑［mα］xm在单位圆之外不可解析开拓。其中R（mα）表示mα的分数部分，［mα］表示mα的整数部分。值得注意的是，赫克指出幂级数系数可在二次域上进行讨论。

C Pisot受赫克工作影响，在《模1数的分布及其代数数》［3］（1938）中把整系数的幂级数和位于单位圆内的共轭代数数类的研究结合起来得到了一些有意义的结果，其中之一为波莱尔关于整系数幂级数在单位圆之外可开拓的重要结论。继Pisot和其他一些人的工作后，R Salem证明了一系列关于具有整系数幂级数理论，清楚地揭示了问题的代数性质。Salem在1949年《具有整系数的幂级数》［4］中从研究P V数的角度出发探讨了整系数幂级数的相关理论。Salem在文末指出，赫克上述定理的证明可不依赖于均匀分布定理，并证明了下列结论，包括了赫克的结果。令φ（n）表示随n无限增大的正有理函数，r（0＜r≤1）为级数∑φ（n）zn的收敛半径，z=r为f（z）=g（z）（z-r）-k的一个极点，ξ为任意实数，则若1/r是一个代数整数；ξg（r）是代数的，且属于有理数域k（r）的两个条件不都满足，则∑［φ（n）ξ］zn。∑［φ（n）ξ］zn以单位圆为自然边界。其证明基于普林斯海姆定理和波利亚—卡尔松定理。该定理由施瓦兹在《无理性幂级数》［5］（1962）中通过扩大数域的方法被进一步推广。Salem感谢Kurt Mahler教授，正是Mahler教授在给他的一封信中，谈及了A Thue（1863—1922）《论无理超越量具备的性质》（1912）的文章，在其中探讨了PV数的性质，这引起了他的注意。

赫克定理可直接取φ（n）=n得到。他同时证得，若级数∑［ξωn］zn，∑［ξωn］zn不以单位圆为自然边界，则ω为一个代数整数。

纽曼同样受赫克工作之影响，在《无理性幂级数》［6］1960）中利用｛nα｝在单位圆内均匀分布（α为无理数）的方法证明了如下定理，把赫克定理一般化。设α为一个实数，g（x）为阶p≥1的多项式，G（x）=∑g（［nα］）xn，则当且仅当α为一个有理数时，G（x）为有理函数。在此定理的基础上，他证得，当且仅当α为一个大于0的有理数时，F（x）=∑x［nα］为有理函数。

“无理性幂级数”的名称来自于纽曼①纽曼发表的论文题目为Irrational power series（1960年），笔者译成《无理性幂级数》。。他的工作奠定了无理性幂级数理论研究的基础，对其他数学家有重要影响。在整个无理性幂级数理论发展的历史中，论文题目中含“无理性幂级数”的论文共有10篇，这10篇论文是有关无理性幂级数理论研究的基石。

2　无理性幂级数理论的早期发展

纽曼的工作首先影响到的是其同事莫德尔。莫德尔在《无理性幂级数》［7］1960）中推广纽曼定理。设f（x，y）是以y的阶大于等于1的x，y的多项式，则F（x）=∑f（n，｛nα｝）xn是x的有理函数，当且仅当α为无理数。莫德尔利用周期函数｛x｝的傅里叶展开、赫克定理和伯努利多项式进行证明。他与纽曼相比，给出的证明更直接和更具有解析性，且对莫德尔而言，只要｛nα｝取无穷多个值就可以了。莫德尔进一步证明了对于无理数α，由级数∑f（n，｛nα｝）xn定义的x的正则函数以单位圆为自然边界。

在该文中，莫德尔把F（x）=∑f（n，｛nα｝）xn转化为了一个重要级数，该级数是他证明所得定理的重要基础。由于该级数的重要性，故他另撰专文进行研究。他在《级数》［8］（1963）中在条件收敛的情况下，讨论了的收敛问题，并成为他后面的两篇文章的理论基础。

数学家施瓦兹利用赫克的方法从另一角度在《无理性幂级数》（1962）中推广了纽曼定理。

设t≥1是一个整数，实函数f（x）在0≤x≤1上至少t+1阶连续可导，且至少存在一个τ，0≤τ≤t-1≤使不等式f（τ）（0）≠f（τ）（1）成立。若α是一个无理数，则幂级数∑f（｛nα｝）zn在单位圆之外不可解析开拓。

施瓦兹在该定理后注释到：若h（x）是一个具有下例性质的实函数，｛h（n）｝（n=0，1，2，…）是取有限个有理数值的周期函数，则在上述定理的假设下，级数∑f（｛nα+h（n）｝）zn在单位圆之外不可开拓。

在施瓦兹之后，对纽曼定理进一步一般化的数学家是H G Meijer。Meijer在《无理性幂级数》［9］（1963）中指出，令k为一个正整数，g（x）为阶p≥1的复域上的多项式，则∑g（［nkα］）xn表示一个x的有理函数，当且仅当α是有理数。他的证明使用了差分理论和均匀分布定理。

Meijer在该文中把纽曼定理亦从其他角度一般化，但未证。设g（x）为一个阶p≥1的复域上的多项式，f（n）为阶k≥1的实系数多项式，对于∑g（［f（n）］）xn成立：

（1）若f（n）的所有系数（可能除常数项外）是有理的，则级数表示x的有理函数。

（2）f（n）的所有非零系数是无理的，且关于有理数域线性独立，若f（x）不含常数项，则级数表示无理函数。

在莫德尔论文的影响下，Meijer猜想在上述定理的条件下，由级数表示的函数在α是无理数的情况下也一定以单位圆为自然边界。该猜想由J Popken在补充条件所有g（x）的系数是代数数的情况下得到圆满解决①Meijer在该文文末感谢Popken教授对他在这个定理上的指导和帮助。。他在《无理性幂级数》［10］（1963）中不仅利用波利亚—卡尔松定理证明了该猜想，而且基于刘维尔代数数逼近定理和Hankel行列式证明了更一般定理。

设g（u）表示代数系数多项式，φ（n）是一个整值算术函数，使得∑g（φ（n）x-n对|x|＞1收敛。则或者它表示一个有理函数，或以单位圆为自然边界的函数。Popken利用该定理推广了波利亚—卡尔松定理。施瓦兹在《无理性幂级数II》［11］1965）中利用波利亚—卡尔松定理证明了Popken所得定理，并对Popken所得定理进一步推广。

D Cantor沿着Popken的研究思路，在《无理性幂级数》［12］（1967）中证明了下列定理。设

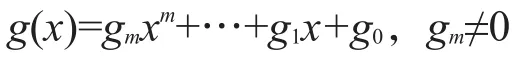
是一个阶m≥1的复系数多项式，

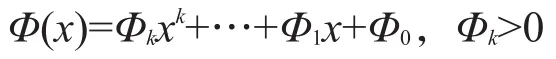
为阶k≥1的实系数多项式。当Φ（x）-Φ（0）为有理系数多项式时，幂级数∑g（［Φ（n）］）zn表示一个有理函数。

这个定理揭示了幂级数系数的算术性质和幂级数表示函数的整体行为的联系。若Φ（x）的系数满足条件，则很容易知道级数表示一个有理函数。基于Popken定理可以直接得到其逆也是对的。

莫德尔在文献［10-11］的基础上，依照施瓦兹1962年上述论文的研究思想在《无理性幂级数II》［13］（1965）中利用赫克的方法和均匀分布理论，推广了施瓦兹1962年的上述定理。

设f（x）=∑φ（｛nα+β｝）xn，|x|＜1，其中α是无理数，β为实数。φ（y）为0≤y≤1的连续函数，则f（x）是x的一个有理函数，当且仅当f（x）为一个有限的傅里叶级数

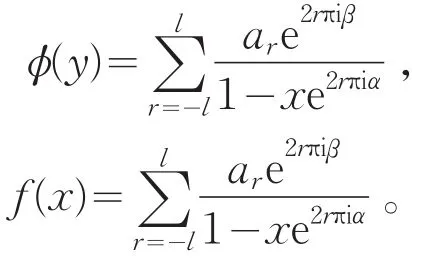
若f（x）不是x的一个有理函数，则f（x）在单位圆之外不可开拓。

莫德尔对这个函数一般化为

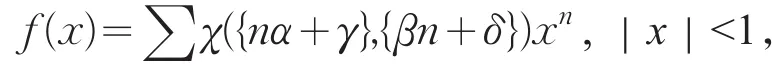
其中χ（y，z）为y，z的函数。α，β为无理数，γ，δ为实数，对任意n，nα+γ或βn+δ为非整数。类似结果在其《无理性幂级数III》［14］（1965）中继续讨论。

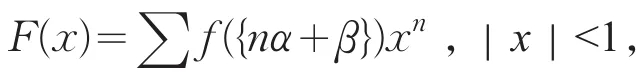
f（x）在0≤x≤1上为黎曼可积函数，且l为任意整数，则沿着半径从x=0趋于e2lπiα时，F（x）（1-xe-2lπiα）收敛于。

若f（x）除有限个点不连续外连续（0≤x≤1），则F（x）是x的有理函数当且仅当f（x）是一个有限的傅里叶级数

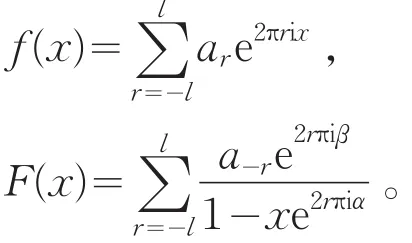
莫德尔把这个定理推广到更一般的级数，在其中f是一个多变量函数。

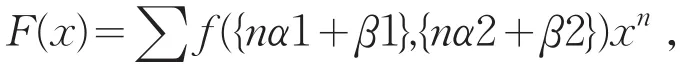
其中α1，α2为无理数，β1，β2为实数。若f（x，y）为0≤x，y≤1上的连续函数，则F（x）是x的有理函数当且仅当f（x，y）是一个有限的傅里叶级数

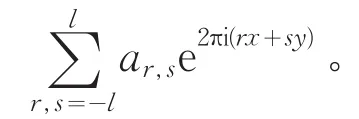
若这个不成立，则F（x）不能在单位圆之外解析开拓。K Nishioka在《某类幂级数的算术性质》［15］（1992）中提到了莫德尔此篇文章的工作，并进一步做了深入研究。

受莫德尔工作的影响，达文波特（Davenport，1907—1969）在《关于无理性幂级数的注释》［16］（1966）中利用和收敛，及e（nt）对一切实数t一致有界条件代替莫德尔定理中的条件对莫德尔的结果以更加一般形式给出，并证明了双重级数的类似结果。P Szusz指出和收敛可由存在代替。J Henniger在《具有概周期系数的幂级数》［17］（1966）中利用系数的概周期条件对达文波特的结果一般化①J Henniger感谢达文波特教授对他这篇文章的指导。。

3　无理性幂级数理论的进一步发展

无理性幂级数理论的进一步发展首先是由F W Carroll和J H B Kemperman做出的。在《不可开拓的解析函数》［18］（1965）中，他们指出，这篇论文的目的是给出以单位圆为自然边界的级数的新类型，其结果和赫克的工作有紧密关系。赫克的方法局限于黎曼可积函数，而他们的方法可以推广到勒贝格可积函数。他们基于实函数列积分的上极限定理得到了如下一个重要定理。

设f（x）在0≤x≤1上勒贝格可积，则幂级数

对一切实数α有收敛半径1。当且仅当f（z）不等于周期为1的三角多项式ΣCpe2pπix时，Fα（z）在单位圆之外不可开拓。

Caroll和Kemperman基于H—序列的概念证明了∑G（［nα］）zn在单位圆外不可开拓，其中

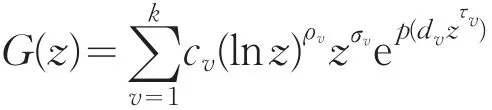
其中ρv，σv，dv，τv（τv＜1），cv为复数。纽曼定理为其特例。

Caroll和Kemperman基于波利亚—卡尔松定理、L—序列的概念证明函数

R Wallisser受Carroll和Kemperman的工作影响，在《不可开拓幂级数的一个定理》［19］1969）中利用维纳定理继续研究幂级数在单位圆内收敛和以其为自然边界问题，并得到一个重要定理。

设函数f（x）以整有理数m≥2为基本周期，f（λ）不相等，λ=0，1，…，m-1。f（x）可以展成一个绝对收敛的傅里叶级数。对m的某个部分g和一切有理整数p≥1，序列（xn/g，xn+p/g）模1均匀分布，则F（z）=∑f（［xn］）zn以单位圆为自然边界。施瓦兹1962年的上述定理为其特例。

施瓦兹和R Wallisser在1973年合作完成了两篇论文，探讨了在单位圆之外不可开拓的幂级数类型。在《论某类不可开拓的幂级数Ⅰ》［20］（1973）中，他们沿着Cantor的研究思想，利用维纳不可开拓判别准则证明了，若Φ（x）-Φ（0）的系数至少有一个是无理数时，∑g（［Φ（n）］+o（nK）zn在单位圆之外不可开拓，K=（m-1）k=gradΦ·（gradg-1）。他们在《论某类不可开拓的幂级数Ⅱ》［21］1973）中，利用维纳判定准则和阿达玛乘积定理对上述定理进行推广，使Popken的上述定理和施瓦兹1965年的上述定理为其特例。

A I Pavlov在前人，特别是莫德尔工作的基础上进行了深入研究。他在《某类幂级数的解析非开拓性》［22］（1998）中构造了整函数G（z）和正整数集合M之间的类（G，M），使得级数

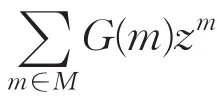
在单位圆外不能解析开拓。莫德尔在1960年的上述定理为其特例。

A I Pavlov在《整函数、解析开拓、一个线性函数的分式部分》［23］（1999）中就G（z）的泰勒系数满足非负条件，通过引入点列偏离理论，利用Wigert定理证明了∑G（［nα］）zn（α∈（0，1）在单位圆之外不能解析开拓。

4　结语

幂级数的系数和其在收敛边界上的行为表现之间有着重要联系，法国数学家阿达玛在1892年明确指出这一点。其后，波莱尔、波利亚、奥斯特洛斯基［24］、斯泽古［25］等数学家研究了函数在收敛域之外是否可以解析开拓的条件，得到了一些重要定理和一些典型的不可解析开拓的例子。伴随着数论理论的发展，不可解析开拓的例子被进一步构造，其中无理性幂级数为其中的重要一类。赫克、纽曼、莫德尔等数学家对此进行了深入研究，并得到了许多深刻结果。外尔均匀分布定理是证明所得结果的重要理论基础。在无理性幂级数理论发展的后一阶段，Caroll和Kemperman等人把这一理论纳入到不可开拓幂级数理论研究中，使其成为特殊情况。

文章基于原始文献，梳理了无理性幂级数理论的发展脉络，揭示了在这一过程中数学家们的数学思想和方法。

［1］王全来.对波莱尔关于函数奇点问题的思想研究［J］.自然科学史研究，2008，27（2）:236-248.

［2］HECKE E.Über analytische Funktionen und die Verteilung der Zahlen modulo Eins［J］.Abh Math Sem Hamburg，1921，1:54-76.

［3］PISOT C.La répartition modulo 1 et les nombres algébriques［J］.Annali di Pisa，1938，7（2）:205-248.

［4］SALEM R.Power series with integral coefficients［J］.Duke Math J，1945，12:153-172.

［5］SCHWARZ W.Irrationale Potenzreihen［J］.Archiv Math，1962，13:228-240.

［6］NEWMAN M.Irrational power series［J］.Proc Amer Math Soc，1960，11:699-702.

［7］MORDELL L J.Irrational power series［J］.Proc Amer Math Soc，1960，12:522-526.

［8］MORDELL L J.The series［J］.J London Math Soc，1963，38:111-116.

［9］MEIJER H G.Irrational power series［J］.Indagationes Math，1963，25:682-690.

［10］POPKEN J.Irrational power series［J］.Indagationes Math，1963，25:691-694.

［11］SCHWARZ W.Irrationale potenzreihenⅡ［J］.Archiv Math， 1965，17:435-437.

［12］CANTORDG.Irrationalpowerseries［J］.Indagationes Math，1967，27:777-786.

［13］MORDELL L J.Irrational power seriesⅡ［J］.Acta Arith，1965，11:181-188.

［14］MORDELL L J.Irrational power seriesⅢ［J］.Proc Amer Math Soc，1965，16:819-821.

［15］NISHIOKA K.Arithmetical properties of a certain power series［J］.J Number Theory，1992，42:61-87.

［16］DAVENPORT H.Note on an irrational power series［J］.Proc Amer Math Soc，1966，17:1-5.

［17］HENNIGER J.Power series with almost periodic coefficients［J］.MathAnn，1967:53-56.

［18］CARROLL F W，KEMPERMAN J H B.Noncontinuable analytic functions［J］.Duke Math J，1965，32:65-83.

［19］WALLISSER R.Einige Sätze über nichtfortsetzbare potenzreihen［J］.Math Z，1970，113:61-67.

［20］SCHWARZ W，WALLISSER R.Über gewisse nichtfortsetzbare potenzreihenⅠ［J］.Mh Math，1973，77:63-66.

［21］SCHWARZ W，WALLISSER R.Über gewisse nichtfortsetzbare potenzreihenⅡ［J］.Monatshefte für Mathematik，1973，77:251-266.

［22］PAVLOV A I.Analytic Noncontinuability of certain classes of power series［J］.Math Notes，1998，64:410-413.

［23］PAVLOV A I.Entire functions，analytic continuation，and the fractional parts of a linear function［J］.Math Notes，1999，66:442-446.

［24］王全来.奥斯特洛斯基在级数超收敛问题上的工作［J］.内蒙古师范大学学报:自然科学汉文版，2013，42（6）: 708-712.

［25］王全来.斯泽古定理的历史研究［J］.纯粹数学与应用数学，2014，30（1）:14-20.

The Origin and Early Development of the Theory on Irrational Power Series

WANG Quanlai
（College of Computer and Information Engineering，Tianjin Normal University，Tianjin 300387，China）

s:This paper discusses the development sequence of the the theory of irrational power series by using historical analysis and comparative methods.M.Newman was the first to put forward the name“Irrational Power Series”.His research aroused other mathematicians'interest in it.Based on Newman's achievement，many mathematicians such as L.J.Mordell and W.Schwarz studied it and got some remarkable results.Other mathematicians such as F.W.Carroll and J.H.B.Kemperman studied it from the point of non-analytic extension power series and propagated relevant results attained by the predecessors.

irrational power series；analytic extension；Weyl uniform distribution theorem；rational function

N09

A

1672-2914（2015）06-0001-05

2015-09-05

国家自然科学基金项目（11571276）。

王全来（1974-），男，天津市人，天津师范大学计算机与信息工程学院副教授，博士，研究方向为近现代数学史。