p-群中不同阶元素的可交换性研究

祁燕

（咸阳师范学院数学与信息科学学院，陕西咸阳712000）

p-群中不同阶元素的可交换性研究

祁燕

（咸阳师范学院数学与信息科学学院，陕西咸阳712000）

对任意两个不同阶元素可交换的p-群进行了研究，得到:（1）当G为方次数为p的p-群时，G中任意两个不同阶元素均可交换；当G为方次数大于p的p-群时，G中任意两个不同阶元素均可交换充分必要条件是Ωe-1（G）≤Z（G）。（2）设G为非交换的p-群，若G中任意两个非正规的子群均有相同的阶，则G中任意两个不同阶元素均可交换。

真子群；Dedekind群；极小非交换群；亚循环群；正规子群

称群G关于k-集具有小平方性质，如果对于群G的任意的k元子集K，都有|K2|＜k2。为了研究具有小平方性质的k-集对有限群的结构的影响，L V Brailovsky和G A Freiman在文献［1］中对关于2-集具有小平方性质的有限群作了一些探讨。随后G A Freiman［2］证明了群G关于2-集具有小平方性质当且仅当它是一个Dedekind群。1989年，Berkovich等［3］又给出了关于3-集具有小平方和小立方性质的有限群的分类。群G关于2-集具有小平方性质，即对任意两个非交换的元素a、b都有a2=b2，本文在Freiman的研究工作的基础上，将2-集小平方性质中的a2=b2换成了o（a）=o（b），对具有这样性质的p-群进行了一些研究。另外，本文中所涉及的符号与术语均参考文献［4-6］。

1　预备知识

证明：由于H是G的真子群，故存在x∈GH。于是对任意的h∈H，都有xh，hx∉H（否则x∈H，与x∈GH矛盾）。这说明，x与H中任何元的乘积均不在H中。下面分两种情况来证明。。

（2）若g∈H，则有g=x-1·xg。由于xg∈G-H，且x-1∈，故

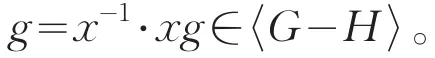
引理2［1］群G关于2-集具有小平方性质当且仅当它是一个Dedekind群。

2　主要定理及其证明

定理1设G为p-群，exp（G）=p，则对任意的a，b∈G，都有o（a）=o（b）或者ab=ba。

证明：若G为交换群，则必有ab=ba（此时，G为初等交换p-群）。若G为非交换群，则由exp（G）=p可知，G是由单位元与p阶元组成。而单位元与G中任意元均可交换，p阶元显然均有相同的阶。

定理2设G为p-群，exp（G）=pe＞p，则G中每两个不同阶元素可交换的充分必要条件是Ωe-1（G）≤Z（G）。

证明：先证必要性。若Ωe-1（G）≤Z（G），则所有的小于等于pe-1阶的元素均包含在Z（G）中心，于是彼此可交换，且与pe阶元可交换。因此，G中任两个不同阶元素均可交换。

再证充分性。设x∈G，且o（x）＜pe，则x∈Ωe-1（G）。若CG（x）=G，则有x∈Z（G），这时Ωe-1（G）≤Z（G）。若CG（x）＜G，则对任意的z∈GCG（x），有o（z）=o（x）。这时我们断言，Z（G）中包含所有的pe阶元。事实上，假设y∈G，且o（y）=pe。则对任意的z∈GCG（x），由o（z）=o（x）＜pe知，o（z）≠o（y），于是z∈CG（y）。因此有G-CG（y）⊂CG（y），从而。由引理1可知。于是CG（y）=G，即y∈Z（G）。从而Z（G）中包含所有的pe阶元。又因为o（xy）=o（y）=pe，所以xy∈Z（G），从而x∈Z（G），这与CG（x）＜G矛盾。因此，Ωe-1（G）≤Z（G）。

定理3设G为非交换p-群。若G的任意非正规子群有相同的阶，则对任意的a，b∈G，都有o（a）=o（b）或者ab=ba。

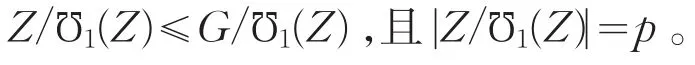
由于G/℧1（Z）内交换且亚循环，故没有循环循环的极大子群。于是Ω1（G/℧1（Z）≤Z（G/℧1（Z），从而

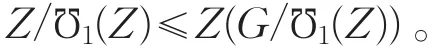
因此Z/℧1（Z）⊲G/℧1（Z），Z⊲G，矛盾。这说明|Z|=pn。于是|H|=pn。这样，G的任意非正规子群有相同的阶。

由定理3与定理4，可以得到下面的推论。

推论1若G是定理4中提到内交换的亚循环p-群，则G中任意两个不同阶元素均可交换。

另外，由引理2，也可以得到以下推论。

推论2若群G是Dedekind 2-群，则G中任意两个不同阶元素均可交换。

证明：由于群G是Dedekind 2-群，故由引理2，G关于2-集具有小平方性质。因此对任意的2元子集M=｛a，b｝，a，b∈G，都有|M2|＜4。而M2=｛a2，b2，ab，ba｝，故若ab≠ba，必有a2=b2。从而o（a）=o（b）。这说明，Dedekind 2-群中任意两个不同阶的元素均可交换。

［1］Brailovsky L V，Freiman G A.On two-element subsets in groups［J］.Annals of the New York Academy of Sciences，1981，373:183-190.

［2］Freiman G A.On two-and three-element subsets of groups［J］. Aequationes Mathematicae，1981，22:140-152.

［3］Berkovich J G，Freiman G A，Praeger C E.Small squaring and cubing properties for finite Groups［R］.Australia:University of WesternAustralia，1989.

［4］徐明曜.有限群导引:上册［M］.北京:科学出版社，1999.

［5］Huppert B.有限群论［M］.姜豪，余曙霞，译.福州:福建人民出版社，1992.

［6］徐明曜，曲海鹏.有限p-群［M］.北京:北京大学出版社，2007.

Permutable Propertities of the Elements Having Distict Orders in p-qroups

QI Yan
（School of Mathematics and Information Science，Xianyang Normal University，Xianyang 712000，Shaanxi，China）

p-groupsGsuch that every two elements ofGof distict orders are permutable are inverstigated，and obtained the following two results:（1）whenGexponent p，then every two elements ofGof distict orders are permutable.whenGexponent greater than p，then all every two elements of Gof distict orders be permutable if only ifΩe-1（G）≤Z（G）.（2）LetGbe nonabelianp-groups，if all nonnormal subgroups have the same order，then every two elemnts ofGof distict orders are permutable.

proper subgroup；Dedekind groups；minmal nonabelian groups；metacyclic groups；normal subgroups

O152.1

A

1672-2914（2015）06-0049-02

2015-07-13

咸阳师范学院科研基金项目（10XSYK203）。

祁燕（1980-），女，山西襄汾县人，咸阳师范学院数学与信息科学学院讲师，研究方向为有限群论。

（1）若g∈GH，则显然g∈