三角代数上Lie中心化子的刻画

王莉莉，马飞，张建华

（1.陕西师范大学数学与信息科学学院，陕西西安710062；2.咸阳师范学院数学与信息科学学院，陕西咸阳712000）

三角代数上Lie中心化子的刻画

王莉莉1，马飞2，张建华1

（1.陕西师范大学数学与信息科学学院，陕西西安710062；2.咸阳师范学院数学与信息科学学院，陕西咸阳712000）

设U是可交换环R上的三角代数，如果线性映射ϕ:U→U，对任意的x，y∈U，当xy=0时，满足ϕ（［x，y］）=［ϕ（x），y］=［x，ϕ（y）］，则存在a∈Z（U）及线性映射τ:U→Z（U），使得对任意x∈U，有ϕ（x）=ax+τ（x），其中τ作用在满足xy=0的交换子［x，y］为零。

三角代数；Lie中心化子；线性映射

设R是环或代数，如果一个可加（线性）映射ϕ：R➝R满足对任意A、B∈R有ϕ（AB）=ϕ（A）B，则称ϕ是左中心化子。如果ϕ（AB）=Aϕ（B），则称ϕ是右中心化子。若ϕ既是左中心化子又是右中心化子，称ϕ是中心化子。关于映射在哪些条件下是中心化子一直是国内外学者们研究的热点问题。Vukman［1］对2-无扰自由半素环A上的可加映射ϕ进行了研究，证明了如果2ϕ（A2）=Aϕ（A）+ϕ（A）A对任意的A∈A成立，则ϕ是中心化子。Vukman［2］对标准算子代数上可加映射ϕ进行了研究，证明了如果对任意A∈R，有ϕ（Am+n+1）= Amϕ（A）An，则ϕ是中心化子。Qi［3］对一般环上的可加映射进行了研究，证明了如果可加映射ϕ对任意A， B∈R满足AB=P，有Aϕ（B）=ϕ（A）B=ϕ（P），则称ϕ是中心化子。与中心化子相关的一些研究结果，可参考文献［4-8］。和中心化子定义相类似，定义Lie中心化子。如果一个可加（线性）映射ϕ:R→R满足对任意A，B∈R，有

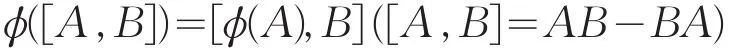
则称ϕ是Lie中心化子。显然，Lie中心化子是中心化子的一种更广泛的形式。最近，Li［9］给出了套代数上Lie中心化子的表达形式。本文将给出三角代数上Lie中心化子的一个刻画。

1　预备知识

设A和B分别是可交换环R上含单位元1A和1B的两个代数，如果M既是左A-模又是右B-模，则称M是（A，B）-双边模。如果对任意的a∈A，b∈B和对任意m∈M满足am=mb=0时，蕴含a=b=0，则称M是（A，B）-忠实双边模，则称

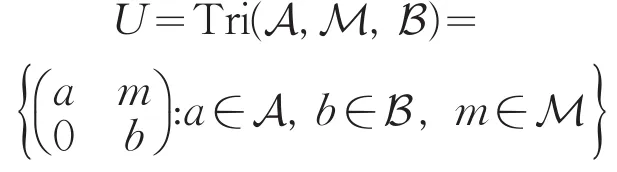
为在通常矩阵运算下的三角代数。

命题1［10］设Z（U）为U的中心，则

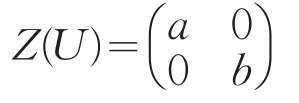
其中a∈A， b∈B且对任意m∈M有am=mb。

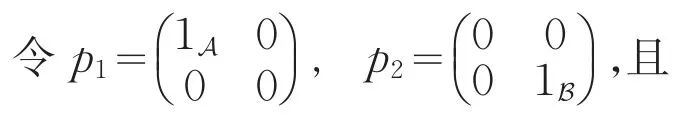
Uij=piUpj（1≤i≤j≤2）。则对任意x∈U，存在xij∈Uij，使得x=x11+x12+x22。定义映射

分别为

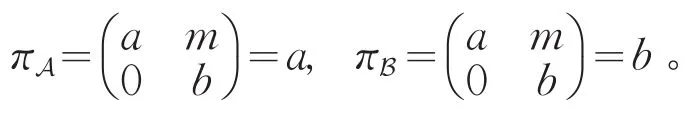
则由命题1可知，πA（Z（U）⊆Z（A），πB（Z（U）⊆Z（B），并且存在唯一的代数同构η:πB（Z（U）→πA（Z（U），使得对任意m∈M，b∈πB（Z（U），有η（b）m=mb。

由命题1可直接验证下面引理1成立。

引理1设U=Tri（A，M，B）是三角代数，如果πA（Z（U）=Z（A），πB（Z（U）=Z（B），则存在唯一的代数同构η:Z（B）→Z（A），使得对任意b∈Z（B），有η（b）⊕b∈Z（U）。

引理2［11］设U=Tri（A，M，B）是三角代数，ϕ:U→U是一个可加映射。

如果对任意的x∈U满足

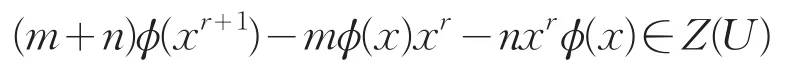
其中m， n， r是正整数。则存在a∈Z（U），使得对任意x∈U，有ϕ（x）=ax。

2　主要定理及证明

定理1设U=Tri（A，M，B）是三角代数且πA（Z（U）=Z（A），πB（Z（U）=Z（B）。如果线性映射φ:U→U对任意的x，y∈U且xy=0，有

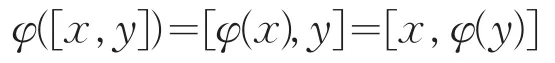
则存在a∈Z（U）及线性映射τ:U→Z（U），使得对任意x∈U，有

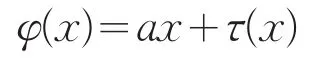
其中τ作用在满足xy=0的交换子［x，y］上为0。

为了证明定理1，需要以下几个断言:

断言1对任意的a12∈U12，有

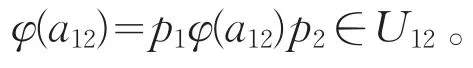
对任意a12∈U12，因为a12p1=0，所以

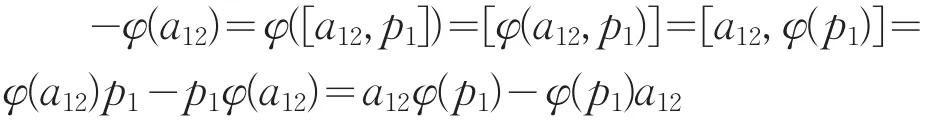
分别对式-φ（a12）=φ（a12）p1-p1φ（a12）两边左右同乘p1和p2，得到

从而有φ（a12）=p1φ（a12）p2∈U12。

断言2存在线性映射τ1:U11→Z（U），使得对任意a11∈U11，有

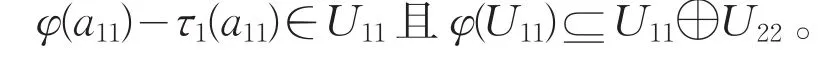
对任意a11∈U11，由于a11p2=0，可得

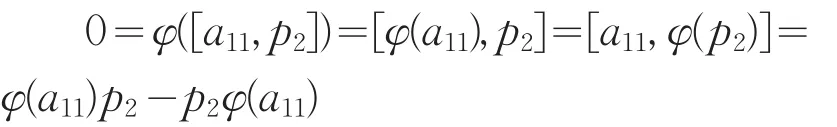
对上式两边左乘p1和右乘p2，得到

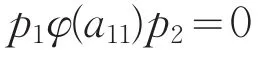
因此φ（U11）⊆U11⊕U22。

现令φ（a11）=b11+b22，其中b11=p1φ（a11）p1，b22=p2φ（a11）p2。对任意a22∈U22，由于a11a22=0，可得

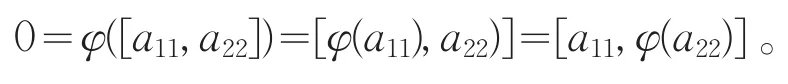
将φ（a11）=b11+b22代入上式，得到

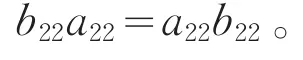
由a22∈U22的任意性，因此，b22∈Z（B）。

由引理1，定义映射τ1:U11→Z（U）为

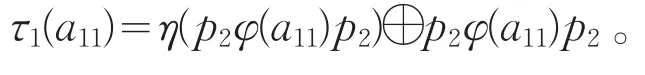
从而

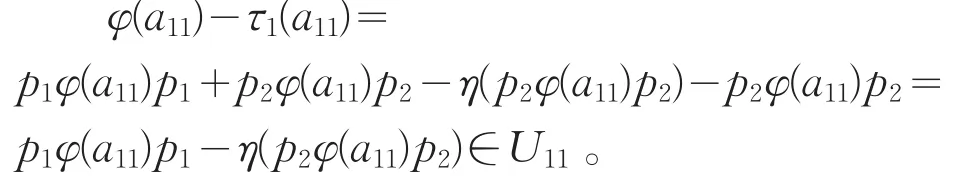
断言3存在线性映射τ2:U22→Z（U），使得对任意a22∈U22，有

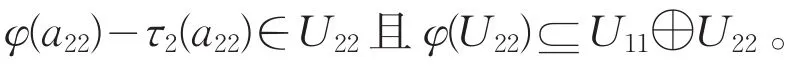
类似断言2的证明过程，可知结论成立。

下面定义线性映射τ:U→Z（U）和d:U→U分别为

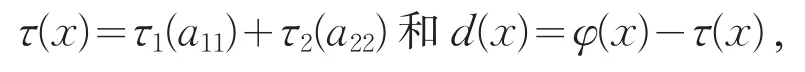
其中x=a11+a12+a22∈U。显然，d（Uij）⊆Uij且d（a12）=φ（a12）。

断言4d是中心化子，并且存在a∈Z（U）使得对任意x∈U，有d（x）=ax。

第一步：对任意a11∈U11，a12∈U12，由于a12a11=0，并根据d（Uij）∈Uij，d（a12）=φ（a12）和τ（x）∈Z（U），可得

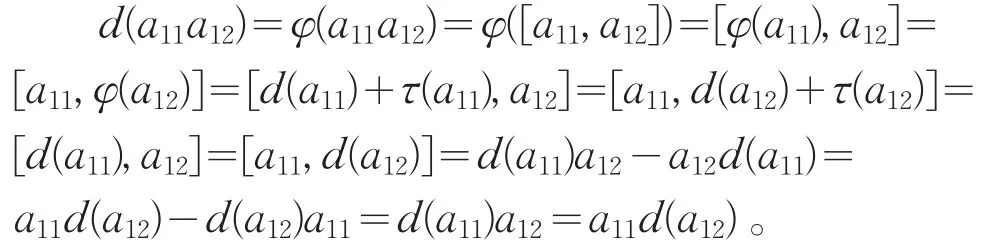
类似的，对任意a12∈U12，a22∈U22，有

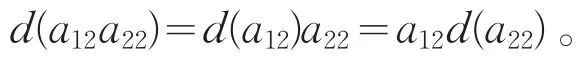
第二步:对任意a11，b11∈U11，a12∈U12，一方面由第一步得

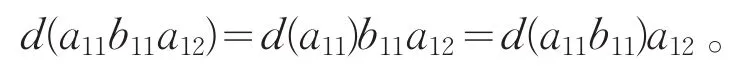
另一方面

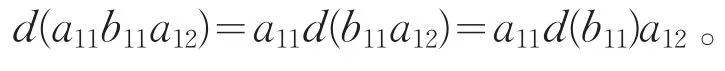
结合以上两个式子，则

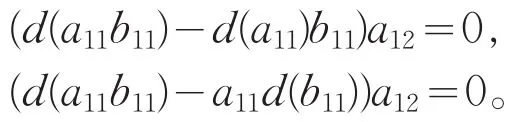
由于M是（A，B）-忠实双边模，从而有

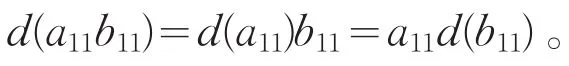
类似的，对任意a22， b22∈U22，有

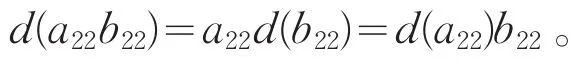
第三步：对任意x， y∈U，有

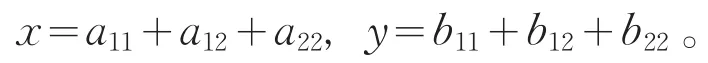
由第一步和第二步知，

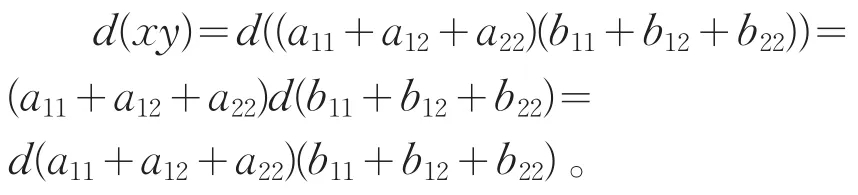
则d（xy）=d（x）y=xd（y）。即d是中心化子。根据引理2可知，存在a∈Z（U），使得对任意x∈U，有d（x）=ax。

断言5τ作用于满足xy=0交换因子［x，y］，有τ（［x，y］）=0。

证明：对任意xy=0，由于τ（x）∈Z（U），可得

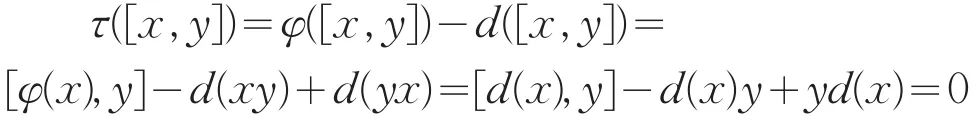
综上所述，定理1成立。证毕。

推论1设H是维数大于2的Hilbert空间，N是H上的非平凡套，AlgN是相关的套代数。如果线性映射φ:AlgN→AlgN对任意x，y∈AlgN，当xy=0时，有

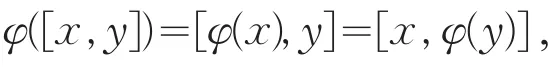
则存在λ∈F及线性映射τ:AlgN→FI，使得对任意x∈AlgN，有φ（x）=λx+τ（x），其中τ作用在满足xy=0的交换子［x，y］为零。

证明：由于AlgN是满足定理1中条件的三角代数，从而由定理1可得该结论成立。证毕。

［1］VUKMAN J.An identity related to centralizers in semiprime rings［J］.Comment Math Univ Carolin，1999，40（3）:447-456.

［2］VUKMAN J，KOSI-UBL I.Centralizers on rings and algebras［J］.BullAustral Math Soc，2005，71:225-234.

［3］齐霄霏.环与算子代数上中心化子的刻画［J］.数学学报:中文版，2013，56（4）:459-468.

［4］MOLNĂR L.On centralizers of an H*-algebras［J］.Publ Math Debrecen，1995，46:89-95.

［5］QI X，DUO S，HOU J.Characterization of centralizers［J］.Acta Math Sinica，Chinese Series，2008，51:509-516.

［6］齐霄霏.J-子空间格代数上的中心化子和广义导子的刻画［J］.数学物理学报:中文版，2014，34（2）:463-472.

［7］VUKMAN J.Centralizers on semiprime rings［J］.Comment Math Univ Carolin，2001，42:237-245.

［8］ZALAR B.On centralizers of semiprime rings［J］.Comment Math Univ Carolin，1991，32（4）:609-614.

［9］李倩，李鹏同.完全分配CSL代数上的中心化子［J］.数学年刊，2011，32A:375-384.

［10］CHENG W S.Lie derivations of triangular algebras［J］.Linear and MultilinearAlgebra，2003，51:299-310.

［11］马飞，李莉，任刚练.三角代数上的中心化子的刻画［J］.计算机工程与应用，2014，49（15）:23-26.

The Characterization of Lie Centralizer on TriangularAlgebra

WANG Lili1，MA Fei2，ZHANG Jianhua1
（1.School of Mathematics and Information Science，Shaanxi Normal University，Xi'an 710062，Shaanxi，China；2.School of Mathematics and Information Science，Xianyang Normal University，Xianyang 712000，Shaanxi，China）

LetUbe a triangular algebra over a commutative ring.Ifϕ:U→Uis a linear map satisfyingϕ（［x，y］）=［ϕ（x），y］=［x，ϕ（y）］for anyx，y∈Uwithxy=0，then it has the form ϕ（x）=ax+τ（x）for allx∈U，wherea∈Z（U）andτ:U→Z（U）is a linear map vanishing at commutators［x，y］withxy=0

triangular algebra；Lie centralizer；linear map

O153.3

A

1672-2914（2015）06-0033-03

2015-04-03

国家自然科学基金项目（11471199）；教育部高等学校博士学科点科研基金（20110202110002）；陕西省教育厅科研计划项目（2010JK890）；咸阳师范学院科研基金项目（14XSYK003）。

王莉莉（1988-），女，陕西商洛市人，陕西师范大学数学与信息科学学院硕士研究生，研究方向为算子代数。

张建华，教授，Email:jhzhang@snnu.edu.cn。