基于广义线性模型的主成分估计及实例分析

杨幼玲

(东北林业大学)

1 预备知识

广义线性模型是经典线性模型的自然推广，它假设因变量为非连续变量，因而实用性较经典线性模型更为广泛.目前对广义线性模型的研究主要集中它的参数估计问题上，当自变量之间存在复共线性时，如果仍然按照原来的参数估计方法进行建模的话，就会带来很大的误差.为了解决这个问题，消除复共线性带来的影响才使得得出的参数估计更为稳定，更符合实际情况的需要，本文将主成分估计应用到广义线性模型中去，并分析其在参数估计较最大似然估计的优越性.

定义1.1［1］设因变量Y和自变量X1，X2，…，Xp的观测值，若

(i)Y1，Y2，…，Yn相互独立，且对每个i，Yi服从指数分布，即

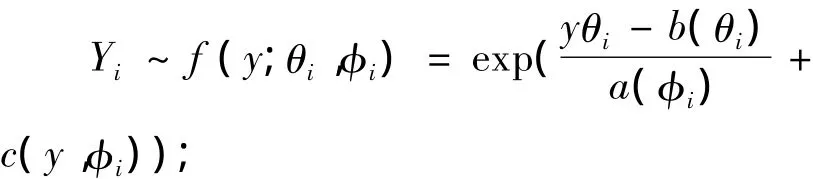
(ii)设ui为对应的Yi的数学期望值(i=1，2，…，n)，存在单调且可导函数g使得ηi=g(ui)=

则称Y与X1，X2，…，Xp服从广义线性模型.

文献［1］中已经给出了广义线性模型的最大似然估计的方法，加权最小二乘法、Newton－Raphson迭代法、Fisher标分法，迭代的结果为

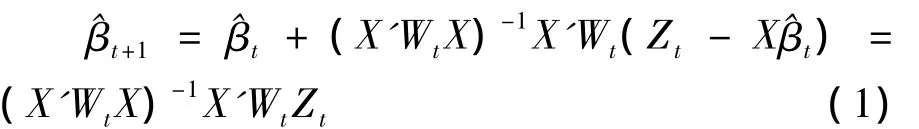
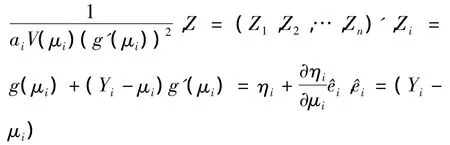
定义1.2［1］若存在不全为0的p个数c1，…，cp使得c1xi1+c2xi2+…+cpxip≈0，i=1，…，n，则称自变量x1，x2，…，xp之间存在复共线性.

当自变量间存在多重共线性关系时，回归分析的结果将受到影响，使得估计值极不稳定，造成一个因素可能取代另一个因素，或几个因素之间相互抵消对因变量的影响，使原来有显著性的因素变得无显著性，而使计算结果变得难以解释.在广义线性模型中，为了克服复共线对自变量造成的影响，在最大似然估计的基础上，对参数估计进行改进引入了主成分估计到广义线性模型中.

2 广义线性模型中的主成分估计

设X为已经中心化的设计矩阵，设计矩阵X'WX的特征值为 λ1，…，λp，则正交矩阵 Φ =(φ1，…，φp)，φ1，…，φp为对应 λ1，…，λp的标准化特征向量，设新的设计矩阵C=XΦ，Φ为p×p正交矩阵，则Φ'X'WXΦ =Diag(λ1)=Λ，设α=Φ'β，又 ηi=g(ui)=Xijβj=Xi'β =Xi'ΦΦ'β=Ci'α.当设计矩阵X存在复共线性时，X'WX的特征值就会很小，近似于0，不妨设λr+1，…，λp≈0.λi度量了第i个主成分值的变动大小，当它的值接近于0时，它对回归自变量的影响将很小可以忽略不计，故可以将它从回归模型中删除.将后面的p－r个主成分删除，得到删除后的部分模型

考虑X'WX=将(2)继续化简

当 λj→0时，会因而将后p－r项主成分直接删去，也就是将(4)式中后p－r项减去即可，这样就得到主成分估计的迭代公式为:

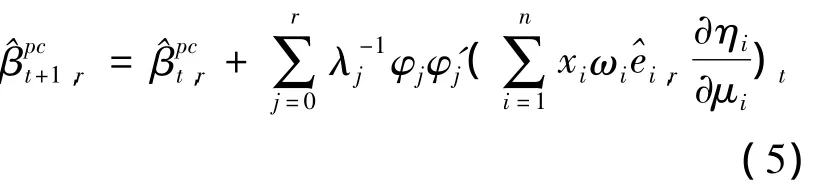
对矩阵进行分块，Φ =(ΦrΦs)，Λ=，其中r+s=p，再由α =Φ'β结合(5)式可得

3 主成分估计优于最大似然估计

定义3.1［2］设θ为p×1未知参数向量，为θ的一个估计,θ的均方误差为

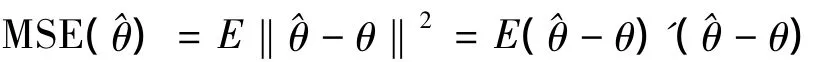
引理3.1［2］MSE(θ)=trCov(θ)+E‖θθ‖2

定理3.1 MSE

证明 由Taylor一阶展开式

由Eg(Y)=g(E(Y))=g(μ)=Xβ代入(6)得

在这里利用了Taylor公式展开项进行了近似处理，省去了对细微条件的把控，方法较为简便，探讨在给定具体条件下最大似然估计的渐近性质可参见文献［6－7］.

定理3.2 设计矩阵出现复共线性时，适当选择保留的主成分估计较最大似然估计的均方误差小，即MSE

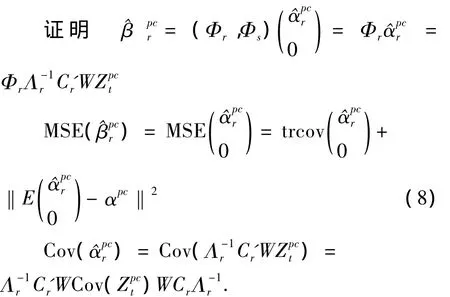
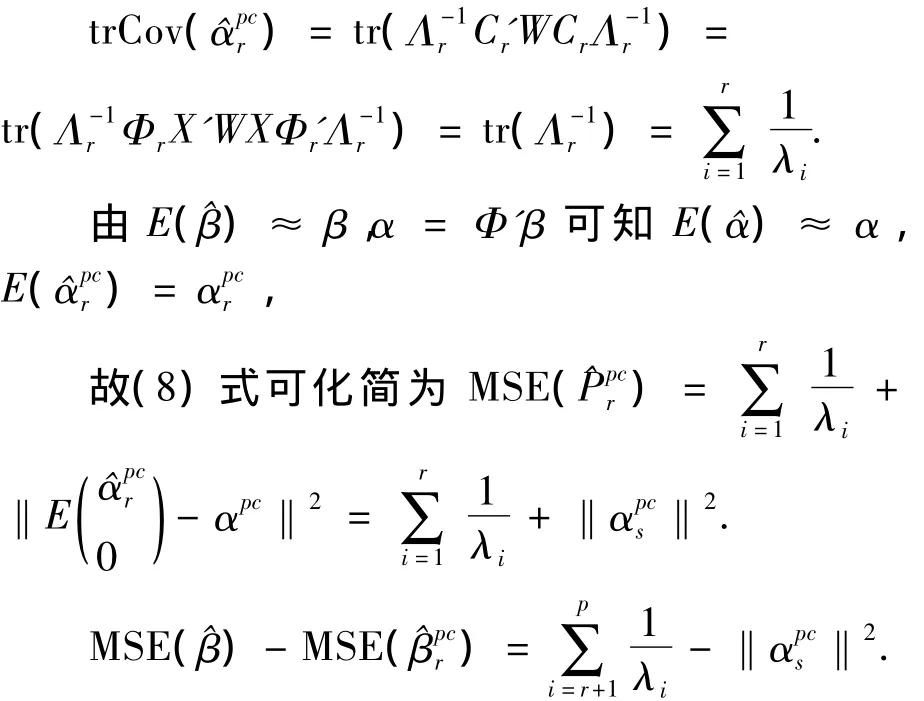
4 实例分析

广义线性模型中很典型的Possion模型为例，分析主成分估计在复共线性诊断中的优良性.数据全部采集于《中国统计年鉴 —2006》［8］的环境保护篇，收集了2005年全国31个地区的大气污染物与污染次数相关的变量，为了消除单位不同而造成的量纲影响，对数据进行原始数据进行标准化后再进行分析，标准化后的数据量有:废气治理设施套数x1;工业二氧化硫排放量x2;工业二氧化硫去除量x3;工业烟尘排放量x4;工业烟尘去除量x5;工业粉尘排放量x6;工业粉尘去除量x7;建成烟尘控制区面积x8;大气污染事件发生的次数y，建立Possion模型:

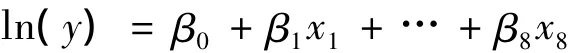
利用R软件对上述数据进行初步分析，剔除分别对应的污染次数为 144、80、69、59、33、31 异常点，直接对模型进行建模，结果得出x4、x5、x6、x8对因变量都不显著，工业中排放的烟尘、粉尘量对空气污染具有很大的影响，显然直接建模得出的结果与实际情况不相符.这时就要考虑是否因变量之间存在共线性，而影响了计算结果.对模型进行主成分分析得出表1的数据.从所得数据可看出后几个主成分的特征值都已经接近于0，因而模型自变量存在复共线性.方差的贡献率表现了其特征值在整体数据中的权重大小，累积贡献率体现了几个主成分共同的权重大小.从计算的结果可看出主成分Z1、Z2、Z3、Z4的方差贡献率较高，而后4个主成分对整体的贡献率几乎不变，因而可以将它们从主成分中舍去，以消除共线性，前4个主成分的累计贡献率较高，已经达到96.2%，将保留的主成分进一步分析，得出主成分的参数估计值.

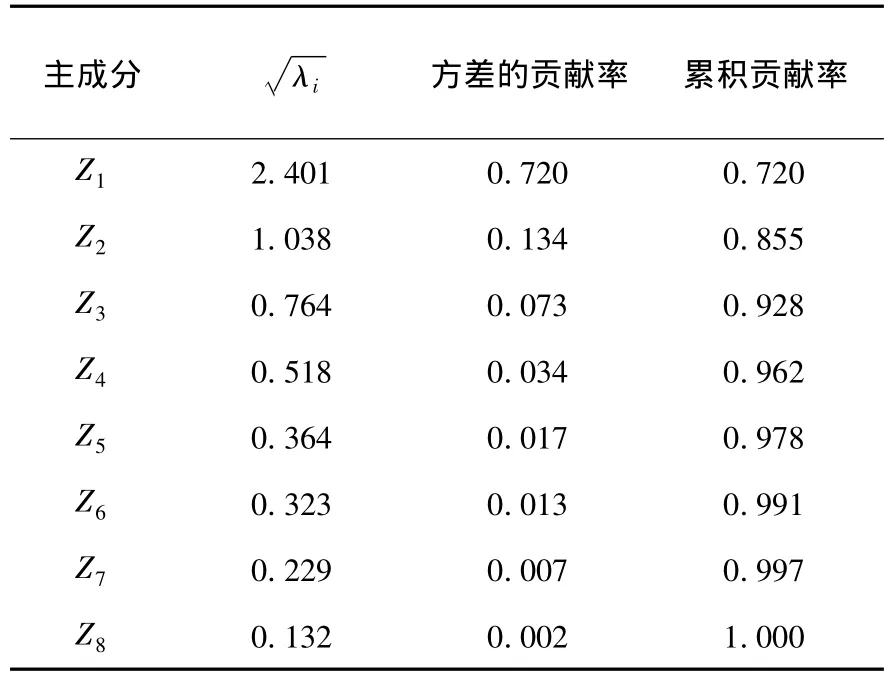
表1 主成分分析结果

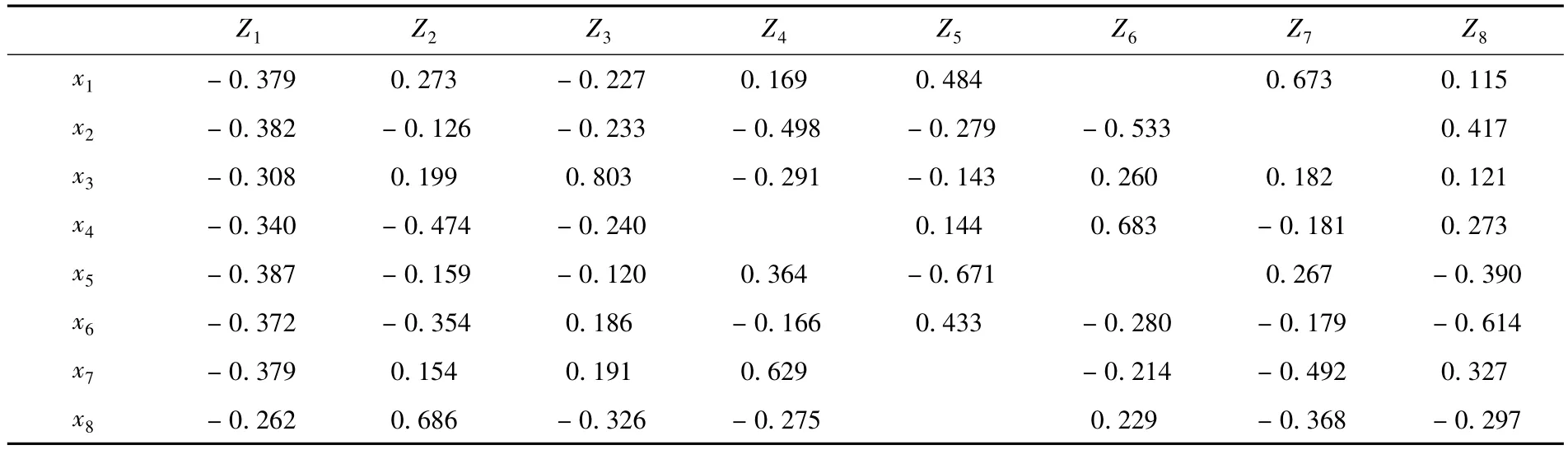
表2 原自变量主成分载荷矩阵

对保留的主成分进行参数估计，可得出如下关系:

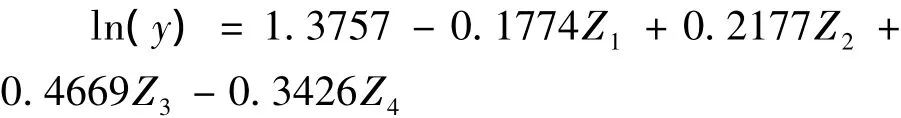
通过前边的数学推导可知保留的主成分是原自变量的线性组合，载荷矩阵计算结果见表2，最后计算的结果为

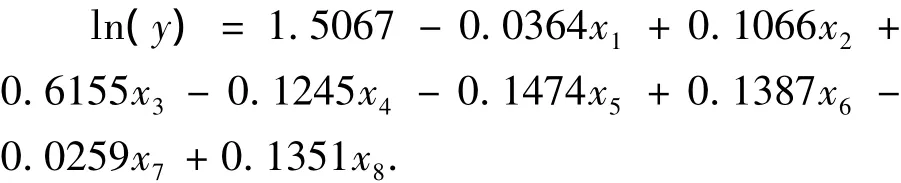
通过计算可知自变量之间存在复共线性，主成分估计得出的结果与实际更为贴切，如果不进行主成分分析，必然会带来很大的计算误差，因而主成分估计在实际应用当中具有非常重要的作用，而且不仅仅只限于传统的经典线性模型.

5 结束语

当自变量中出现复共线性关系时，广义线性模型的主成分估计的均方误差比最大似然估计小，在理论上说明了其优于最大似然估计.文中列举的例子同样也说明了，自变量出现了复共线性，如果忽略这个因素直接建模的话，必然使最后计算出来的系数无法解释每个变量确切的关系，因而主成分估计是广义线性模型中消除自变量复共线性关系的很好的方法.

［1］梅长林，王宁.近代回归分析方法［M］.北京:科学出版社，2012.

［2］王松桂，陈敏，陈立萍.线性统计模型:线性回归与方差分析［M］.北京:高等教育出版社，1999.

［3］何晓群，刘文卿.应用回归分析［M］.北京:中国人民大学出版社，2001.

［4］McCullagh P，Nelder J A.Generalized Linear Models［M］.Library of congress card numberm，1999:99–13896.

［5］Marx BD.Principal component estimation for generalized linear regression［J］.Biometrika，1990，77(1):23–31.

［6］Wedderburn R W M.On the existence and uniqueness of the maximum likelihood estimates for certain generalized linear models［J］.Biometrika，1976，63(1):27－32.

［7］Fahrmeir L，Kaufmann H.Consistency and asymptotic normality of the maximum likelihood estimator in generalized linear models［J］.Ann Statist，1985，13:342－368.

［8］国家统计局.中国统计年鉴－2006［G］.北京:中国统计出版社，2006.

［9］薛毅，陈立萍.统计建模与R软件［M］.北京:清华大学出版社，2007.