Richards增长曲线的参数估计*

乔 钰，徐文科

(东北林业大学)

1 Richards增长曲线方程

Richards模型的微分形式［1］为

方程(2)可以简写为

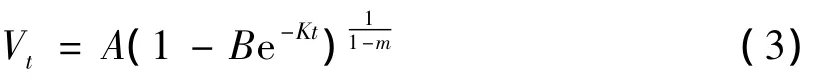
2 线性最小二乘法估计Richards增长曲线参数

令m－1=δ，并将(3)式中的因变量Vt用y(t)表示，(3)式可表为

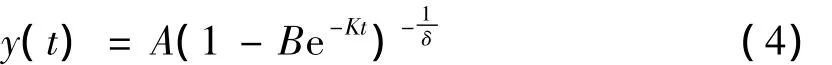
对(4)式取对数求导整理可得

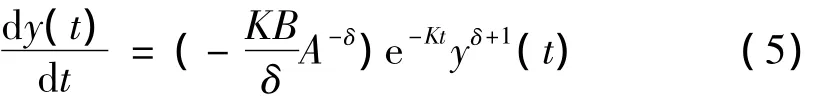
令－BA－δ=C，并对(5)式取对数，可得

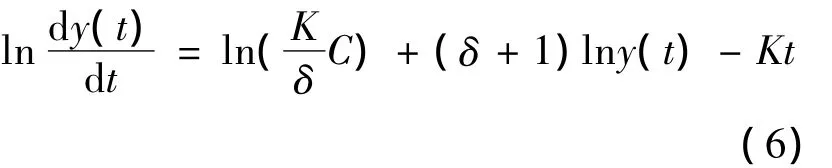
用向后差分 Δhy(t)=y(t)－y(t－1)代替设误差为e(t)，所以由(6)式可得

lnΔhy(t)= β0+β1lny(t)+β2t+e(t)(7)将(7)式写为矩阵形式:

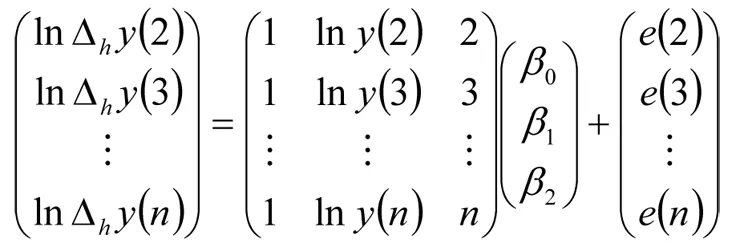
同时记

上式等价于

(8)式和(9)式为线性模型，则

因此由(10)式就可以估计出 β0，β1，β2的值，进而可以估计出δ，K，C的值.

由－BA－δ=C及(4)式可解得

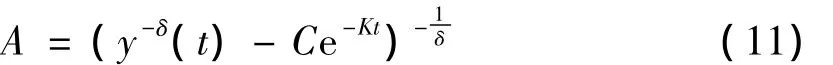
将(tmax，ymax)代入上式得A的估计值，进而得B的估计值

综上所述，Richards增长曲线方程的四个参数得以估计.

3 双向差分误差平方和最小估计法估计Richards增长曲线参数

针对Richards增长曲线

仍做取对数求导处理得到(6)式

记号

分别称为y(t)在t处的向前差分和向后差分.用向前差分Δqy(t)和向后差分Δhy(t)分别取近似导数，用eq(t)，eh(t)分别表示向前差分的近似误差和向后差分的近似误差.

向前差分近似误差:

向后差分近似误差:

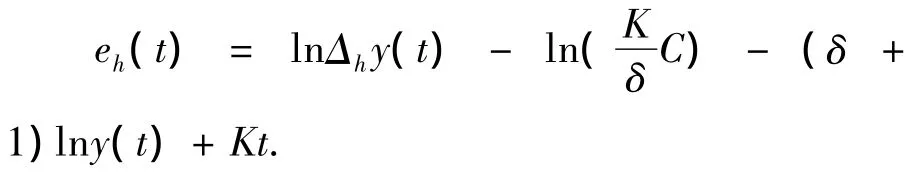
定义一个关于误差的评价指标—向前差分和向后差分总的误差平方和

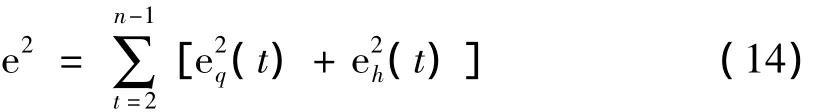
使向前差分和向后差分误差平方和达到最小，也就是需满足:

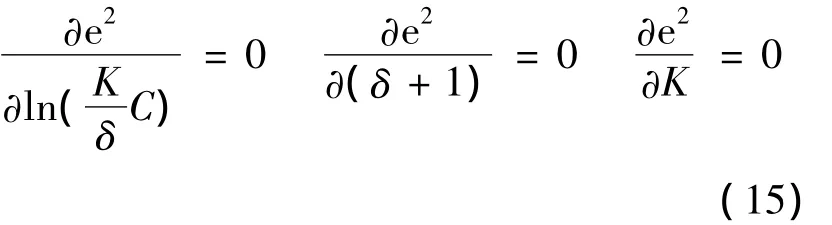
将(12)，(13)式代入(14)式，计算(15)式，并令［ln(y(t)－y(t－1))+ln(y(t+1)－y(t))］整理可得:

定义:

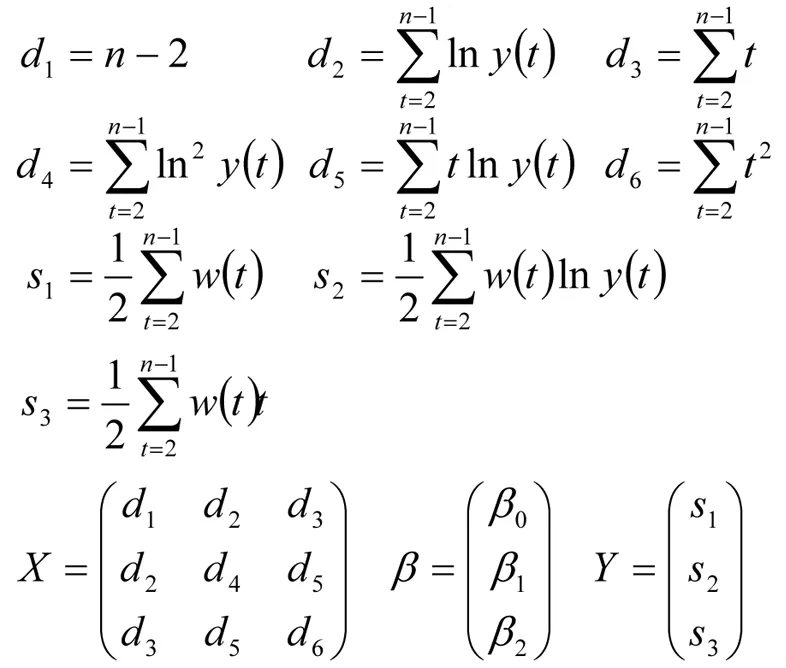
则(16)，(17)，(18)可改写为

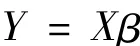
从而得到β的最小二乘估计

由(19)式可得K，δ，C的估计值.

对饱和值A的估计以及B的估计与线性最小二乘法中的参数估计方法完全相同.

综上所述，Richards增长曲线的四个参数得以估计.

4 双向差分加权最小二乘法估计Richards增长曲线参数

y(t)在t处以步长为1的向前差分和向后差分用如下记号表示:

向前差分 Δqy(t)=y(t+1)－y(t).

向后差分 Δhy(t)=y(t)－y(t－1).

由于每次观测中对向前差分和向后差分的偏重不同，设v(t)(t=2，3，…，n–1)，1–v(t)，表示在第t次观测中向前差分和向后差分占的比例且0≤v(t)≤1，Y(t)=v(t)Δq(t)+(1－v(t))Δh(t)表示在第t次的观测值.若在第t次观测中偏向于向前差分或者向后差分，那么相应的权重就取较大的值.

用Y(t)=v(t)Δq(t)+(1－v(t))Δh(t)代替(6)式中的微分= δ+1，β2=–K，则有

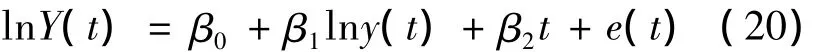
则由(20)式得到的近似误差为:

将(20)式写成矩阵形式:

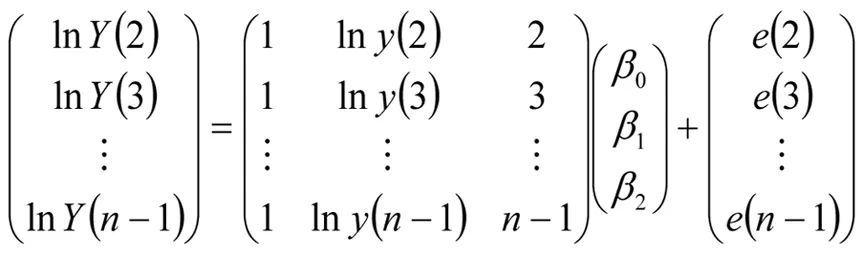
同时记

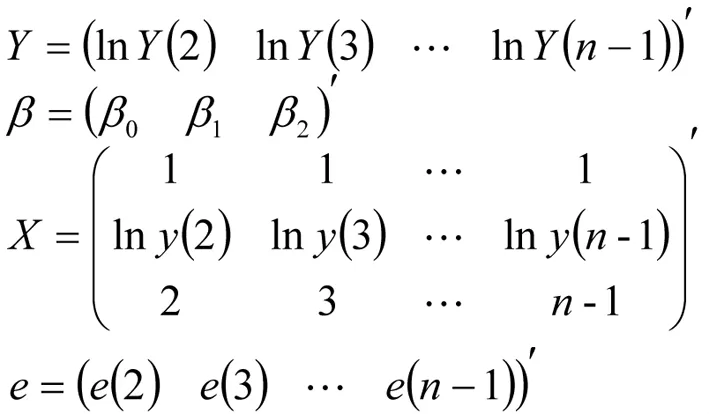
上式等价于

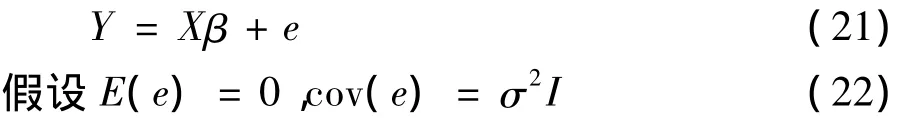
(21)式和(22)式为线性模型，则

由(23)式求得K，δ，C.对参数A，B的估计同上.

利用此方法，该曲线方程的所有待估参数得以估计.

5 模型应用

为了说明Richards生长曲线方程参数估计的有效性以及说明Richards方程的适用性，现以2003年北京市4月到5月的 SARS疫情数据［5］(见表1)为例，对Richards模型进行拟合，并列出几个拟合结果.

模型的拟合误差选用

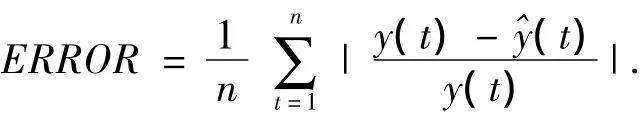
利用R软件计算得到模型的拟合结果:

拟合结果1:线性最小二乘估计法估计得到A=2537.0，B=– 2.0225，K=0.3021，δ=0.5613;ERROR=0.0107.

表1 原始数据及其拟合结果

拟合结果2:双向差分误差平方和最小二乘估计法计算得到A=2532.3，B=–1.1731，K=0.2995，δ=0.3855;ERROR=0.0143.

拟合结果3:应用双向差分加权最小二乘估计，假设各误差都相等且不相关，权重系数为v(2)=v(3)= …v(n－1)=0.25，得到估计值A=2538.3，B =－1.2669，K =0.2914，δ =0.4071;ERROR=0.0071.

比较模型的拟合误差ERROR的大小，可以看出双向差分加权最小二乘估计法比线性最小二乘法以及双向差分误差平方和最小法能更好的估计模型参数，拟合误差最小.

6 结束语

用线性最小二乘估计法、双向差分误差平方和最小估计法和双向差分加权最小二乘估计法对Richards增长曲线方程的参数进行了估计，最后应用到具体实例中，实例证明拟合精度较高.

［1］Richards F J.A flexible growth function for empirical use［J］.J Exp Bot，1959，10(29):290–300.

［2］Pienaar L V.Chapman－Richards generalization of von Bertalanffy’s growth model for basal area growth and yield in even－ aged stands［J］.For Sci，1973，19(1):2–22.

［3］Lin Zhaogang，Li Fengri.The generalized Chapman－Richards function and applications to tree and stand growth［J］.Journal of Forestry Research，2003，14(1):19–26.

［4］刑黎峰.生物生长的 Richards模型［J］.生物数学学报，1998，13(3):348–353.

［5］程毛林.Richards模型参数估计及其模型应用［J］.数学的实践与认识，2010，40(12):139–143.

［6］徐文科，张石生.生物种群Logistic模型双向差分拟合方法及对初始预报值的改进［J］.农业系统科学与综合研究，1997，13(1):1–3，9.

［7］徐文科.基于微分方程的生态数学模型统计分析［D］.东北林业大学博士论文，2009.

［8］徐文科，刘洋.捕食与被捕食种群似乎不相关模型的参数估计［J］.黑龙江大学:自然科学学报，2013，30(5):570–575.