s－半条件置换子群对超可解性的影响 *

张 玥，钱方生

(哈尔滨师范大学)

0 引言

利用子群的各类置换性质来研究有限群的超可解性是一个重要手段.设A，B为群G的两个子群，如果AB=BA，那么A被叫做与B可置换的;群G的一个子群H如果与G的所有子群可置换，则称H为G的置换子群或拟正规子群.置换子群的概念被广泛的推广，郭文彬等在文献［1］中引入了条件置换子群的概念，并且利用他们已经成功得到了有限群结构的一系列新的结果;黄建红在文献［2］中进一步减弱条件置换的条件，得到了s－条件置换子群的概念，并研究了s－条件置换子群的性质，利用子群的s－条件置换性质给出了有限群的结构;林辉在文献［3］中进一步弱化了s－条件置换子群的条件，定义了s－半条件置换子群的概念:群G的子群H在G中称为s－半条件置换的，如果对于群G的任一Sylow子群T，只要(|H|，|T|)=1，就存在x∈G，使得HTx=TxH.该文试图根据有限群的4阶循环子群的s－半置换的性质对群超可解性给出一定的结论.

1 预备知识

定义1 群G的子群H称为在G中s－半条件置换，如果存在G中的任一Sylow子群T，只要(|H|，|T|)=1，就存在一个元素x∈G，使得HTx=TxH.

定义3 设G是有限群，记SE(G)为G的最大超可解嵌入子群，它是G中一切超可解嵌入子群之积.

定义4 设G为有限群，x∈G，如果对任意的y∈G都＜x＞＜y＞=＜y＞＜x＞，则称x为G的拟中心元，由G的所有拟中心元生成的子群成为G的拟中心记为Q(G).

定义5 设G为有限群，G的拟超中心Q∞(G)是下述子群链的最大项1=Q0(G)≤Q1(G)≤Q2(G)≤ … 其中Qi(G)/Qi－1(G)=Q(G/Qi－1(G))(i=1，2，…).

引理1.1［3］设G是有限群且H≤G，则下列结论成立:

(1)若H在G中是s－半条件置换的且H为一个p－群，则HK/K在G/K中是s－半条件置换的.

(2)若HK/K在G/K中是s－半条件置换的且K⊆H，则H在G中是s－半条件置换的.

(3)若H在G中是s－半条件置换的且H≤M≤G，则H在M中是s－半条件置换的.

(4)若HK/K在G/K中是s－半条件置换的且(|H|，|K|)=1，如果G可解或K幂零，则H在G中是s－半条件置换的.

(5)若H在G中是s－半条件置换的且H为一个p－群，则H∩K在G中是s－半条件置换的，且H∩K在K中是s－半条件置换的.

引理1.2［4］设G是内超可解群，则G有如下结构

(1)存在正规子群P∈Sylow(G)，使得G=P∞M，P/Φ(P)为G/Φ(P)的非循环的极小正规子群.

(2)如果P＞2，则 exp=p，若p=2，则exp≤4且p2||G|.

(3)存在c∈PΦ(P)，使＜c＞不是G的正规子群.

(4)如果P为Abel群，则Φ(P)=1.

(5)如果P不为Abel群，则Φ(P)=Z(P)=P.

(6)G为Sylow塔群或G为内幂零群.

引理1.3［5］(Schur－ Zassenhaus定理)设N为G的正规Hall子群，则N在G中有补群.

2 主要结果

定理1 如果G的极小子群都包含在SE(G)中，且G的4阶循环子群在G中s－半条件置换，则G为超可解群.

证明 假设定理不成立，而设G为极小阶反例.

(1)G为内超可解群.事实上，对于任意子群K＜G，因为K的任一极小子群H≤SE(G)∩K≤SE(G)，由引理1.1知K的4阶循环子群在G中s－半条件置换，从而在K中s－半条件置换，所以K满足定理条件，由G的极小性知，K超可解，故G为内超可解群，从而G具有引理1.2的结构.

(2)设P为G的正规Sylowp－子群，如果exp(P)=p，由条件知P≤SE(G)，从而由G/P超可解知G超可解，所以必有p=2，如果G有Sylow塔性质，则由p=2知G=P×M超可解，矛盾.故由引理1.2知G为2aqb阶的内幂零群.

(3)若存在a∈PΦ(P)，使得o(a)=2.设＜x＞为G的Sylowq－子群，令M=＜a，ax…axqb－1＞≤P，则MΦ(P)/Φ(P)◁G/Φ(P)，由G/Φ(P)的极小性知M，因为＜axqi＞≤SE(G)，1≤i≤b，所以P≤SE(G)，于是由G/P超可解知G超可解，矛盾.

(4)导出矛盾.因为G为内超可解群，故存在P∈ Syl2(G)， 使得Φ(P) 为G/Φ(P)的极小正规子群，且P/Φ(P)非循环，设H为G的p－补，任取Hq∈Sylq(H)，则Hq∈Sylq(G)，因为对任意的g∈PΦ(P)有＜g＞在G中s－半条件置换，从而存在Q∈Sylq(G)，q∈π(G)且q≠p使得＜a＞Q成群，

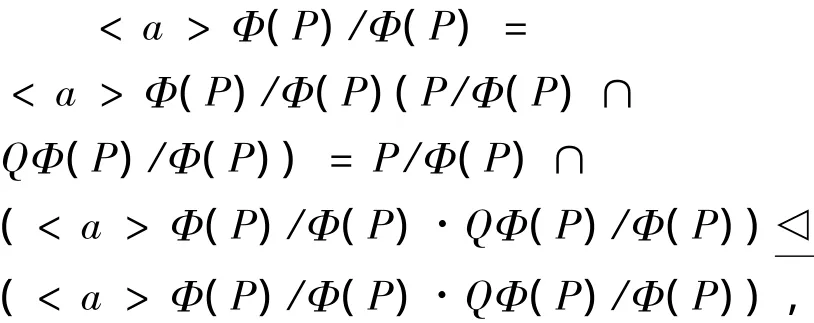
从而

QΦ(P)/Φ(P)≤NG(＜a＞Φ(P)/Φ(P))，又P≤NG(＜a＞Φ(P)/Φ(P))，

于是

故极小阶例不存在，G为超可解群.

推论1 设N为G的正规子群使得G/N超可解，若N的极小子群均属于SE(G)且4阶循环子群在G中s－半条件置换，则G为超可解群.

定理2 设N为G的正规子群使得G/N超可解，若N的极小子群均属于Q∞(G)且4阶循环子群在G中s－半条件置换，则G为超可解群.

证明 假设定理不成立，而设G为极小阶反例.

(1)G为内超可解群.

事实上，对于任意子群K＜G，因为K/(K∩N)≌KN/N≤G/N，故由G/N超可解知，K/(K∩N)超可解，又因为K∩N的极小子群包含K∩Q∞(G)≤Q∞(K)中，K∩N的4阶循环子群在K中s－半条件置换，所以条件对子群遗传，由G的极小性知，K超可解，故G为内超可解群.

(2)由引理1.2知，G有正规的Sylowp－子群P，使得P/Φ(P)为G/Φ(P)的极小正规子群，由引理1.3知，G有p－补.设H为G的p－补，则G/P≌H超可解，由于G/N为超可解群，故G/(P∩N)为超可解群，如果P∩N≤Φ(P)，则G/Φ(P)为超可解群，从而G/Φ(G)为超可解群，于是G为超可解群，矛盾.故P∩N不包含在Φ(P)中，因此1≠G/Φ(P)，但(P∩N)Φ(P)/Φ(P)≤Ρ/Φ(P)，且P/Φ(P)为G/Φ(P)的极小正规子群，所以P=(P∩N)Φ(P)=P∩N，从而P≤N，可见P也为N的Sylowp－子群.如果exp(P)=p，由条件知P≤Q∞(G)，从而由G/P超可解知G超可解，矛盾.所以必有p=2，如果G有Sylow塔性质，则由p=2知G=P×M超可解，矛盾.故由引理1.2知G为2aqb阶的内幂零群.

(3)任意a∈PΦ(P)，使o(a)=2.因为G为2aqb阶的内幂零群，故由引理 1.2知exp(P)≤4且4||G|，假设存在a∈PΦ(P)，再设＜x＞为G的Sylowq－子群，令M=＜a，ax…axqb－1＞≤P，则MΦ(P)/Φ(P)由G/Φ(P)的极小性知，P=MΦ(P)=M，因为＜axqi＞≤Q∞(G)，1≤i≤b，所以P≤Q∞(G)，于是由G/P超可解知G超可解，矛盾.

(4)导出矛盾.因为G为内超可解群，故存在P∈ Syl2(G)， 使得为G/Φ(P)的极小正规子群，且P/Φ(P)非循环，设H为G的p－补，任取Hq∈Sylq(H)，则Hq∈Sylq(G)，因为对任意的g∈PΦ(P)有＜g＞在G中s－半条件置换，从而存在Q∈Sylq(G)q∈π(G)且q≠p使得＜a＞Q成群，

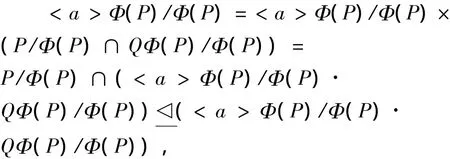
从而

又P≤NG(＜a＞Φ(P)/Φ(P))，

于是

故极小阶反例不存在，G为超可解群.

推论2 若G的极小子群均属于Q∞(G)且4阶循环子群在G中s－半条件置换，则G为超可解群.

［1］Guo W B，Shum K P，Alexander S.Conditionally permutable subgroups and super solubility of Finite groups［J］.Southeast Asian Bulletion of Mathematices，2005，29:493–510.

［2］黄建红，郭文彬.有限群的s－条件置换子群［J］.数学年刊，2007，28A(1):17－26.

［3］林辉.有限群的s－半条件置换子群与p－超可解性［J］.佛山科学技术学院报:自然科学版，2008，26(5):11－14.

［4］陈重穆.内外∑－群与极小∑－群［M］.重庆:西南师范大学出版社，1988.1–90.

［5］徐明耀.有限群导引:上册［M］.北京:科学出版社，1999.

［6］胡玉生.超拟中心与有限群的超可解性［J］.阜阳师范学院学报:自然科学版，2010，12(4):27.

［7］胡玉生.完全条件置换子群与有限群的超可解［J］.长春工业大学学报:自然科学版，2010，12(6):31.

［8］张远达，等.幂零与可解之间［M］.武汉:武汉大学出版社，1988.

［9］Huppert B.有限群论Ⅰ:中译本［M］.福州:福建人民出版社，1992.

［10］陈重穆.内外群与极小非群［M］.重庆:西南师范大学出版社，1988.