适应性回归分析(Ⅳ)
——与非适应性回归分析的比较
2019-06-18罗艳虹胡良平
罗艳虹,胡良平
(1.山西医科大学公共卫生学院卫生统计学教研室,山西 太原 030001;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029;3.军事科学院研究生院,北京 100850
1 概 述
相对于因变量是“计数变量”和“定性变量”而言,因变量为“计量变量”的回归建模方法的种类更多。其中,若按是否采用“适应性回归分析”可划分为以下两类:适应性回归分析[1-2]与非适应性回归分析[3-12]。在非适应性回归分析方法中,最常用且最有代表性的就是多重线性回归分析方法,在SAS软件中,可以通过REG过程来实现。
本文将采用ADAPTIVEREG过程和REG过程来实现对同一个数据集的回归建模,并结合数据集和数据子集的真实情况,反映并揭示两种建模思想对数据集和数据子集的建模效果。从而得出对回归建模及建模效果评价有意义的参考性建议。
2 问题与数据结构
2.1 原问题与数据集
沿用本期科研设计方法专题中第二篇文章《适应性回归分析(II)——排除噪声变量的干扰》(以下简称“前文”)中的“问题与数据结构”,其数据集名为“artificial”。
2.2 新问题与数据集
在原问题中,数据集artificial包含一个因变量y及其取值,10个在(0,1)区间上服从均匀分布的随机变量x1~x10及其取值;y是x1和x2的函数,并具有“前文”式(1)的表达式。整个数据集的样本含量N=400。随机变量x3~x10是独立于因变量y的,或者说,它们是与因变量y无关的随机变量。
2.3 扩展的数据集
2.3.1 扩展的数据集a1
在数据集artificial的基础上,引入由随机变量x1~x10产生的派生变量[3],它们是由随机变量x1~x10的全部二次项组成,共55项(包括10个平方项和45个交叉乘积项)。连同随机变量x1~x10共有65个自变量,所得的数据集为a1。所需要的SAS数据步程序如下:
data a1;
set artificial;
z1=x1*x1;z2=x1*x2;z3=x1*x3;
z4=x1*x4;z5=x1*x5;z6=x1*x6;
z7=x1*x7;z8=x1*x8;z9=x1*x9;
z10=x1*x10;z11=x2*x2;z12=x2*x3;
z13=x2*x4;z14=x2*x5;z15=x2*x6;
z16=x2*x7;z17=x2*x8;z18=x2*x9;
z19=x2*x10;z20=x3*x3;z21=x3*x4;
z22=x3*x5;z23=x3*x6;z24=x3*x7;
z25=x3*x8;z26=x3*x9;z27=x3*x10;
z28=x4*x4;z29=x4*x5;z30=x4*x6;
z31=x4*x7;z32=x4*x8;z33=x4*x9;
z34=x4*x10;z35=x5*x5;z36=x5*x6;
z37=x5*x7;z38=x5*x8;z39=x5*x9;
z40=x5*x10;z41=x6*x6;z42=x6*x7;
z43=x6*x8;z44=x6*x9;z45=x6*x10;
z46=x7*x7;z47=x7*x8;z48=x7*x9;
z49=x7*x10;z50=x8*x8;z51=x8*x9;
z52=x8*x10;z53=x9*x9;z54=x9*x10;
z55=x10*x10;
run;
【说明】在上面的程序中,“z1=x1*x1”和“z11=x2*x2”分别代表x1与x2的平方项;“z2=x1*x2”代表x1与x2的交叉乘积项;z3~z10代表与x1有关的交叉乘积项;z12~z19代表与x2有关的交叉乘积项。也就是说,z1~z19或多或少与因变量y有一定的联系。z20~z55这36个变量都独立于因变量y;另外,由前面的介绍可知,随机变量x3~x10是独立于因变量y的,故独立于因变量y的自变量共有44个(即x1~x10,z20~z55)。
2.3.2 扩展的数据集a2
由于因变量y是计量变量,故可以对其进行变量变换。常规的变量变换方法有以下五种:对数变换、平方根变换、倒数变换、指数变换和Logistic变换[13-15]。在数据集a1基础上,引入对因变量y的上述五种变换,分别记为y1~y5,所得的数据集为a2。所需要的SAS数据步程序如下:
data a2;
set a1;
y1=log(y+5);y2=sqrt(y+5);y3=1/(y+5);
y4=exp(y+5);y5=exp(y+5)/(1+exp(y+5));
run;
【说明】因为在因变量y的取值中,出现了负数和零,不便于取对数和平方根变换,统一加上一个正数5即可。
数据集a2中包含了数据集a1,而其又包含了数据集artificial,故以下仅基于数据集a2进行计算即可。
2.3.3 数据集a2中变量的分类
因变量有6种表现形式,分别为原先的形式y、取了不同变量变换后的形式y1~y5;自变量可分为以下两类:A类中含有21个与因变量有关系的自变量,即“x1和x2,z1~z19”;B类中含有44个与因变量无关系的自变量,即“x3~x10,z20~z55”。
3 基于a2数据集中A与B两类共65个自变量进行回归建模
3.1 采用ADAPTIVEREG过程对65个自变量进行回归建模
3.1.1建模策略
分别选取y、y1~y5为因变量,利用65个自变量(其中,A类21个自变量与因变量有关系,B类44个自变量与因变量无关系),采用ADAPTIVEREG过程进行回归建模。
3.1.2 建模结果
建模的输出结果较多,下面仅给出自变量对因变量贡献排名前五位的自变量及反映其重要性大小的百分数。见表1。

表1 ADAPTIVEREG过程对65个自变量进行回归建模给出前五位自变量及其重要性数值
由表1可知:分别以“y、y1和y2”为因变量时,ADAPTIVEREG过程从65个自变量中提取的前五位重要的自变量全部属于A类中的自变量;而分别以“y3、y4和y5”为因变量时,ADAPTIVEREG过程从65个自变量中提取的前五位重要的自变量中分别有4、3、3个属于A类中的自变量,即出错数目分别为1、2、2个。
3.2 采用REG过程对65个自变量进行回归建模
3.2.1建模策略
分别选取y、y1~y5为因变量,利用65个自变量(其中,A类21个自变量与因变量有关系,B类44个自变量与因变量无关系),采用REG过程进行回归建模。具体地说,在假定模型包含截距项与不含截距项的条件下,再分别采用“前进法”“后退法”和“逐步法”筛选自变量,并记录下最终回归模型的有关重要信息。
3.2.2 建模结果
建模的输出结果较多,下面仅给出最终的回归模型中分别包含A类与B类自变量的数目。见表2。

表2 REG过程对65个自变量进行回归建模保留A与B类自变量的数目
由表2可知:假定回归模型中不含截距项时,保留在回归模型中的自变量数目明显增多,此时,有很多与因变量无关的自变量会被保留在最终的回归模型之中。假定回归模型中包含截距项且采用前进法或逐步法筛选自变量时,回归模型中保留与因变量无关的自变量的数目比较少,即结论的正确性较高。
4 基于a2数据集的B类中44个自变量进行回归建模
4.1 采用ADAPTIVEREG过程对B类中44个自变量进行回归建模
4.1.1建模策略
分别选取y、y1~y5为因变量,利用B类中44个自变量,采用ADAPTIVEREG过程进行回归建模。
4.1.2 建模结果
建模的输出结果很多,为节省篇幅,下面仅给出自变量对因变量贡献排名前五位的自变量及反映其重要性大小的百分数。见表3。由表3可知:尽管B类中44个自变量独立于因变量,但ADAPTIVEREG过程仍以较高的“重要性”数值保留了较多的自变量。

表3 ADAPTIVEREG过程对B类中44个自变量进行回归建模给出前五位自变量及其重要性数值
4.2 采用REG过程对B类中44个自变量进行回归建模
4.2.1 建模策略
分别选取y、y1~y5为因变量,利用B类中44个自变量,采用REG过程进行回归建模。具体地说,在假定模型包含截距项与不含截距项的条件下,再分别采用“前进法”“后退法”和“逐步法”筛选自变量,并记录下最终回归模型的有关重要信息。
4.2.2 建模结果
建模的输出结果较多,下面仅给出最终的回归模型中包含B类自变量的数目。见表4。
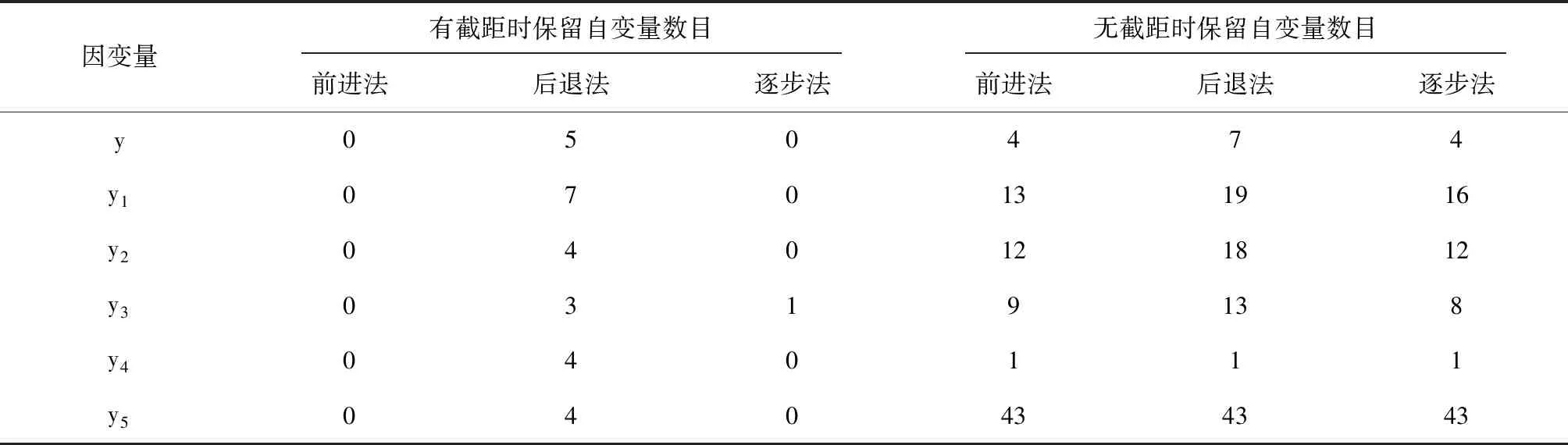
表4 REG过程对B类中44个自变量进行回归建模保留自变量的数目
由表4可知:假定回归模型中包含截距项且采用前进法筛选自变量时,与因变量无关的自变量全部都不被保留在回归模型中,结果最可信;假定回归模型中包含截距项且采用逐步法筛选自变量时,与因变量无关的自变量几乎都不被保留在回归模型中(本例仅因变量y3时有一个自变量),结果比较可信;而假定回归模型中不含截距项且采用“指数变换(因变量y4)”时,与因变量无关的自变量被保留在回归模型中的数目最少(本例中出现了一个);假定回归模型中不含截距项且采用Logistic变换(因变量y5)时,与因变量无关的自变量被保留在回归模型中的数目最多(本例中出现了43个)。
5 回归建模所需要的SAS程序
5.1 实现表1和表3计算的SAS程序
5.1.1 实现表1计算所需要的SAS过程步程序
proc adaptivereg data=a2;
model y=x1-x10 z1-z55;
quit;
5.1.2 实现表3计算所需要的SAS过程步程序
proc adaptivereg data=a2;
model y=x3-x10z20-z55;
quit;
5.1.3 关于上述SAS程序的说明
将因变量y依次修改为“y1~y5”,分别运行上面的SAS过程步程序。
5.2 实现表2和表4计算的SAS程序
5.2.1 实现表2计算所需要的SAS过程步程序
proc reg data=a2;
model y=x1-x10 z1-z55/selection=forward sle=0.05;
quit;
proc reg data=a2;
model y=x1-x10 z1-z55/noint selection=forward sle=0.05;
quit;
5.2.2 实现表4计算所需要的SAS过程步程序
proc reg data=a2;
model y= x3-x10 z20-z55/selection=forward sle=0.05;
quit;
proc reg data=a2;
model y=x3-x10 z20-z55/noint selection=forward sle=0.05;
quit;
5.2.3 关于上述SAS程序的说明
将“model语句”中的“selection=”及其后面的内容分别修改为“backward sls=0.05;”和“stepwise sle=0.5 sls=0.05;”,就是采用“后退法”和“逐步法”筛选自变量;将因变量y依次修改为“y1~y5”,分别运行上面的SAS过程步程序。
6 讨论与结论
6.1 讨论
统计学教科书上所讲授的、统计软件中所实现的回归分析方法,主要依据是数学原理和数理统计知识;实际工作者在运用回归分析技术时,并不知晓资料的自变量中哪些与因变量有关系、哪些与因变量无关系,全依靠回归分析技术和统计软件计算的结果来作出肯定或否定的结论。
基于本文的“数据结构”“真实情况”和“两种回归建模思路及计算结果”,可提出以下问题:在通常情况下,使用回归分析技术处理各种“真实情况未知”的试验数据时,所得到的“回归分析结果”的可信度究竟有多高?究竟应该如何提高回归分析结果的可信度?
笔者认为:对于“真实情况未知”的试验数据而言,无论采用“参数法”“半参数法”“非参数数”或所谓的“机器学习或深度学习”等方法进行回归建模,都是在“无中生有”,其整个过程都是一个“黑箱”,结果的可信度在相当大的程度上取决于资料中变量之间的真实情况。然而,当研究者对资料的真实情况一无所知时,应采取非常审慎的态度看待其分析结果。
6.2 结论
当资料中存在与因变量确有关系的自变量时,①由表1可知,ADAPTIVEREG过程具有较好的甄别能力;当对因变量采取对数变换或平方根变换时,其甄别能力下降;当对因变量采取倒数变换或指数变换或Logistic变换时,其甄别能力下降较为明显。②由表2可知,REG过程具有较好的甄别能力,但需要满足一定条件,即采用“前进法”或“逐步法”筛选自变量,同时还需要“假定模型包含截距项”。
当资料中不存在与因变量确有关系的自变量时,①由表3可知,ADAPTIVEREG过程几乎完全失去了甄别能力;②由表4可知,REG过程具有较好的甄别能力,但需要满足一定条件,即采用“前进法”筛选自变量,同时还需要“假定模型包含截距项”。若对因变量采取指数变换且“假定模型不含截距项”时,无论采取“前进法”“后退法”或“逐步法”筛选自变量,都具有较好的甄别能力(见表4中倒数第2行最后3个数据,从44个独立于因变量的自变量中仅错误地保留了一个自变量)。若研究者基于基本常识和专业知识确定的自变量都与因变量有关系,对因变量进行Logistic变换,并且,假定回归模型中不含截距项时,会在回归模型中保留非常多的自变量。此时,反映模型对资料拟合效果的R2值非常接近1、均方误差MSE的数值远远小于1(因输出结果较多,未在表2和表4中呈现出来)。
