具有幂零根 nn，1 的一类可解李代数的Hom－结构 *

刘慧莹，谢文娟

(哈尔滨师范大学)

0 引言

Hom－李代数是李理论的一个重要研究方向，研究Hom－李代数的目的与李代数的量子形变有关，李代数的量子形变是量子论群理论研究的重要课题.2006年，Hartwing，Larsson和Silvestrov在研究Witt代数和Virasoro代数的量子形变时引进了Hom－李代数的概念［1］.近年来，人们对Hom－李代数的研究也取得了许多重要的成果.该文主要计算了一类可解李代数的Hom－结构.

由Levi’s定理，知道任何有限维李代数都同构于一个半单李代数和一个最大可解理想的直和［2］.由于任何可解李代数都有唯一确定地幂零根基.因此，研究可解李代数的工作主要归结于研究其不同的幂零根基.该文主要计算了特征零的代数闭域F上的一类具有自然阶化filiform幂零根nn，1的可解李代数的Hom－结构.

1 预备知识

定义1.1［1］设(g，［·，·］)是一个李代数，φ:g→g是一个线性映射，若以下Hom－Jacobi等式:

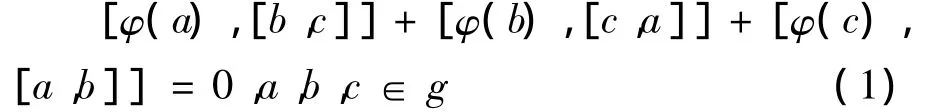
成立，则称(g，［·，·］，φ)为Hom－李代数，称 φ为李代数g的Hom－结构.若Hom－结构φ还是李代数同态，则称φ为李代数g的保积Hom－结构.

显然，一个李代数g上的所有Hom－结构关于线性映射的加法和数乘构成一个向量空间，记作HS(g).

定义1.2［3］定义一个L的理想的序列:

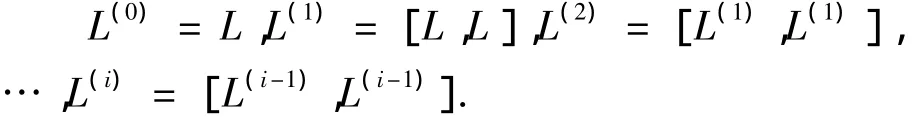
若对某一个n有L(n)=0，则称L是可解李代数.

定义 1.3［4］幂零代数nn，1是具有一组基{e1，…，en}的李代数，并且满足如下李乘运算.

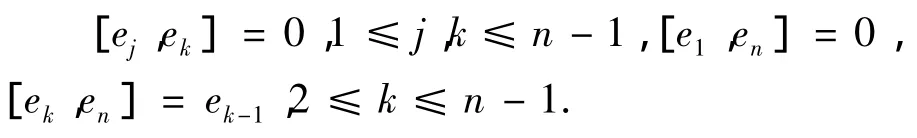
引理1.4［5］对于任意的n≥4，具有基{e1，…，en，x}的幂零根同构于nn，1的n+1维可解李代数有以下三类:

(i) Sn+1(α，β) :

这种类型中互不同构的是Sn+1，1(β)=Sn+1(1，β)

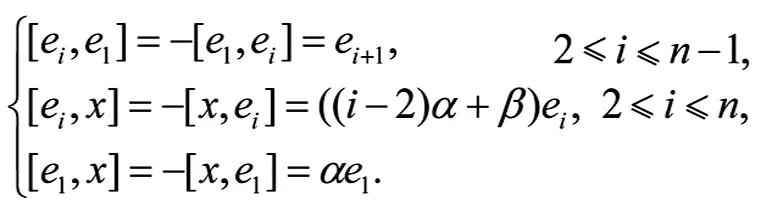
和Sn+1，2=Sn+1(0，1).

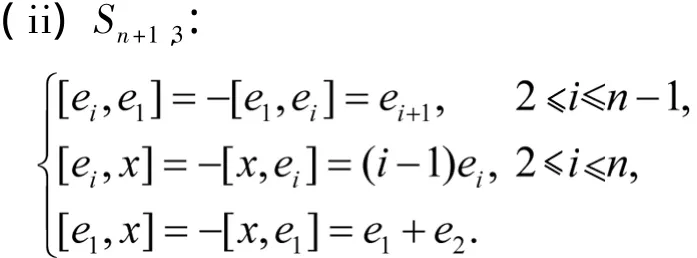
(iii)Sn+1，4(a3，a4，…，an－1):

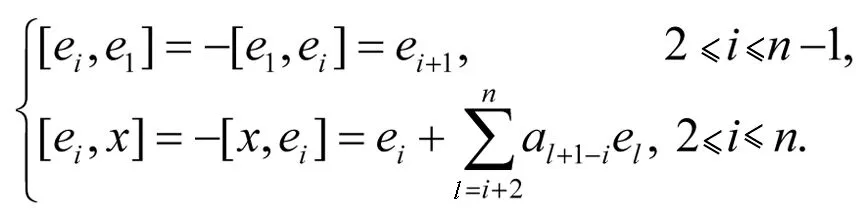
其中第一个非零的系数{a3，…，an－1}可以设为1.

2 主要结果

该文主要计算了上述引理1.4中的第二类可解李代数Sn+1，3的Hom–结构.

定理2.1 设F是特征零的代数闭域，Sn+1，3是F上具有幂零根nn，1的有限维可解李代数，则

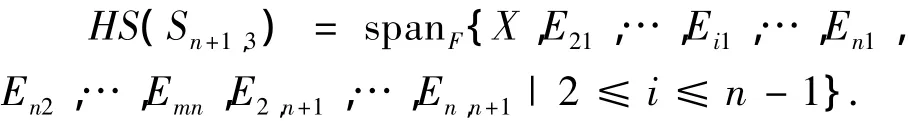
其中X=a)E11+(2b－a)E22+…+(ib+(1－i)a)Eii+…+bEn+1，n+1.

证明 设 φ ∈HS(sn+1，3)，它在基{e1，…，en，x}下的矩阵为

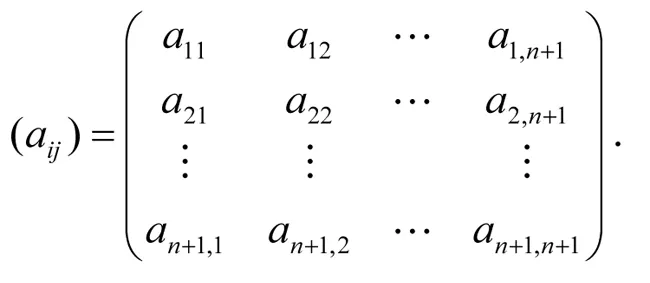
于是由Hom－Jacobi等式(1)可进行计算.

(1)当取a，b，c为e1，ei，ej，其中2 ≤i≤j≤n－1时，有如下两种情况:

(i)当j≠i+1 时，由［φ(e1)，［ei，ej］］+［φ(ei)，［ej，ei］］+［φ(ej)，［e1，ei］］=0，可得–a1iej+2–jan+1，iej+1+a1jei+2+ian+1，jei+1=0，即a1i=0，an+1，i=0，a1j=0，an+1，j=0，2 ≤i＜j≤n－2.

当取i=n–1 或j=n–1 时，有an+1，j=0，a1，n－1=0，an+1，n－1=0，

(ii)当j=i+1 时，e1，ei，ej即为e1，ei，ei+1.

由［φ(e1)，［ei，ej］］+［φ(ei)，［ej，ei］］+［φ(ej)，［e1，ei］］=0，

当2 ≤i≤n– 3 时，有a1i=0，an+1，i+1=0，a1，i+1=(i+1)an+1，i，

当i=n– 2 时，有a1，n－1=(n– 1)an+1，n－2=0，an+1，n－1=0，

当i=n– 1 时，有an+1，n=0.

(2)当取a，b，c为e1，ei，en，其中2 ≤i≤n–2 时，由 Hom－Jacobi等式(1)，有a1n=0，an+1，n=0.

当i=n– 1 时，同理有an+1，n=0.

(3)当取a，b，c为e1，ei，x，其中2 ≤i≤n–2 时，由Hom－Jacobi等式(1)，有aii=ian+1，n+1+(1–i)a11，aki=0，k≠i，1≤k≤n–1，2≤i≤n– 2，an+1，i=0，ai－1，i=– (i－1)2an+1，1=0，ai+1，i=a1，n+1=0，2 ≤i≤n– 2.

(4)当取a，b，c为e1，en－1，x时，由 Hom–Jacobi等式(1)，有an－1，n－1=(n– 1)an+1，n+1+(2－n)a11，ak，n－1=0，1 ≤k≤n– 2，an+1，n－1=0，an－2，n－1=– (n– 2)2an+1，1=0.

(5)当取a，b，c为e1，en，x时，同理由 Hom–Jacobi等式(1)，有a1n=a2n=a3n= …an－2，n=an－1，n=an+1，n=0.

(6)当a，b，c取其它基元素时，Hom－Jacobi等式(1)恒成立.

综上，φ 在基［e1，…，en，x］下的矩阵可表示如下:

［1］Harywig J，Larsson D，Silvestrov S.Deformations of Lie algebras using σ－derivations［J］.J Algebra，2006，295:314–361.

［2］Li Xiaochao，Li Dongya，Jin Quanqin.A Class of Solvable Lie Algebras and Their Hom－Lie Algebra Structures［J］.Chin Quart J of Math，2014，29(2):231－237.

［3］Tremblay S，Winternitz P.Solvable Lie algebras with triangular nilradicals［J］.J Phys A，1998，31:789–806.

［4］Snobl L，Winternitz P.A class of solvable Lie algebras and their Casimir invariants［J］.J Phys A，2005，38:2687–2700.

［5］Casas J M，Ladra M，Omirov B A，et al.Classification of solvable Leibniz algebras with naturally graded filiform nilradical［J］.Linear Algebra and its Applications，2013，438(7):2973－3000.