从负折射现象重新认识波

杜春光

（清华大学物理系，北京 100084）

波是物理学中的一个极其重要的基本概念，在经典物理中，波可以简单描述成某种振动在空间中的传递.例如，机械波可以看作是机械振动在介质中的传递，电磁波可以看作是电场和磁场的振动在真空或介质中的传递.在量子力学中，波是一个基本概念，它与粒子概念相伴，形成互补，有着极其深刻的物理内涵.随着科学和技术的不断发展，人们对波动现象的认识也在不断深化.从当今物理学的发展看，大量新奇物理现象都源于量子力学中的波动性概念.但是，我们不禁会反思：在经典物理理论的框架内，是否也有一些需要重新理解的问题？就波动概念而言，无论是经典意义上还是量子意义上，都存在一个共同的需要深度思考的问题，即，如何理解波的传播速度.这一问题给人们带来了许多困惑，同时推动人们开展了一系列新的研究，包括介质中的反常相速度和群速度.例如，关于相速度，有负折射现象[1]；关于群速度，有超慢传输现象[2]，还可能在增益的介质中获得超过真空光速的群速度[3].这些现象都已经在特殊的介质中实现，近年来已被大量研究.就负折射率材料而言，目前的实现手段主要是通过人工微结构方法，微结构的单元类似原子或分子，它们比波长小，但仍然是宏观尺度的，实现这种功能的材料称作特异材料或超材料（metamaterial）[4]，其物理机制通常是经典的（理论模型中电磁场和介质中的电子都视为经典的）.

负折射现象近年来被大量研究，但对这一新问题，以往的分析都比较复杂，涉及的知识面较广，将相关概念和方法引入到大学物理教学中仍然存在一定的困难.例如，关于折射率什么情况下取负值的问题，以往的分析虽然也是从因果律出发，但论证较为复杂，涉及的数学推导过多，对初学者而言，不易把握其物理实质.在物理教学中，如何用简单直观的方式解释负折射现象仍然有待于研究.另一方面，负折射现象给人们带来的启示是多方面的，例如：（1）能够激发人们更深入思考电磁场的运动方程的物理含义；（2）更深入研究介电常数、磁导率、折射率等重要物理量的微观起源；（3）推动人们开展相关新现象和新应用的研究；（4）由于波动现象存在共性，负折射现象有可能获得广泛推广.基于以上几点，将负折射现象引入到物理教学中是十分有益的.本文考虑到大学物理的知识体系，给出了简单的理论推演，重新分析了麦克斯韦方程及其求解过程，自然给出了“负折射”解，并结合常规边界条件，分析了负折射材料非凡的物理特性.本文还进一步分析了负折射现象的微观起源，并讨论了其可能的推广及给人们带来的启示.

1 根据因果律确定相速度的方向

为简单起见，先考虑一个沿着z方向传播的单色平面电磁波，假设是线偏振的，电场方向沿x方向，则电场函数可写成

观察这一波函数，很容易知道相位传递的速度为

对实际介质，由于电磁波与其内部电子在相互作用时难免会存在能量损耗，因此，严格讲k应该是一个复数，k的虚部代表吸收，从方程（1）可以看出，如果k的虚部大于零，则电场E随z而减小.本文只考虑吸收很小的情况，这时k的虚部可当作正无穷小量，方程（2）仍然可以用来计算相速度的绝对值，但相速度的方向需要根据因果律来判断.我们可以根据k的虚部为正这一事实，判断出相位速度的方向.其证明如下：

根据因果律，如果波源放在一个均匀的无边界的被动（无增益）介质中，则波总是由波源向外辐射.于是，考虑到介质的损耗，方程的解中的电场E随传播距离应该是逐渐减小的，而不能是指数增长的（指数增长的解在无穷远处发散，为非物理解，必须舍弃）.考虑沿z正方向的传播（即假设波源在左，观测者在右），这时只能取k的虚部为正的解（它代表电磁波随z衰减，是合理的解），而不能取k的虚部为负的解（它代表E随z增长，将导致能量放大，并在无穷远处发散，这是不合理的解，必须舍去）.但是，一个容易引起困惑的问题出现了：k的虚部为正时实部一定为正吗？这对普通正折射率介质的确都是成立的，但理由常常被误解为相位传递的方向必须由波源指向观测者，负折射的研究已证明这是个误区.以下分析将发现，对负折射率介质，k的实部和虚部是异号的.由于因果律要求k的虚部为正，所以此时k的实部和相速度必然为负值.下面从电磁运动的基本方程出发证明这一点.

2 从基本方程导出“负折射解”

考虑电磁波在常规介质中的传播（不考虑增益介质情况），假设没有自由电荷与传导电流，电磁场满足麦克斯韦方程组

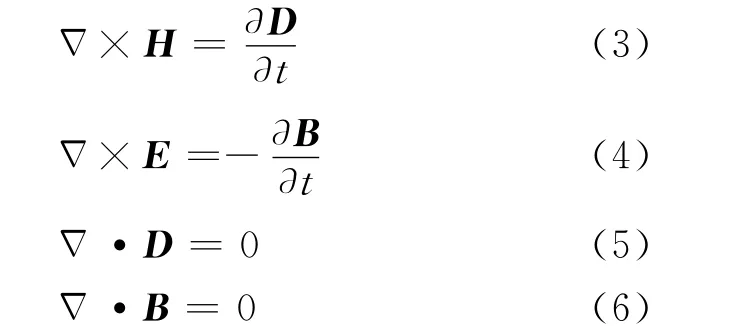
对相对介电常数和相对磁导率分别为ε、μ的材料，其本构关系为

对实际的介质，都存在吸收和色散，为方便起见，方程（2）中各个物理量都采用复数形式（电场E和磁场B的实际值取以上方程解的实部）.由于介质的响应存在滞后，ε和μ均为复数，其虚部不为零，这源于介质对电磁波的吸收，这一点后面从微观机制角度分析.

从式（3）～（8）出发我们可以得到电场所满足的波动方程

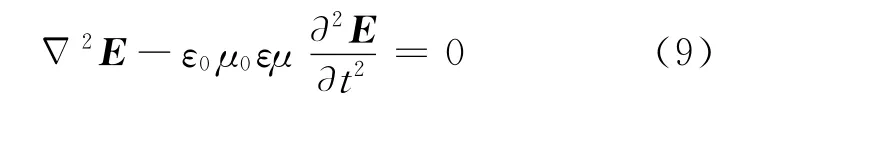
把平面单色波电场表达式E（z）＝E0eikz-iωt代入波动方程，可以得到色散关系

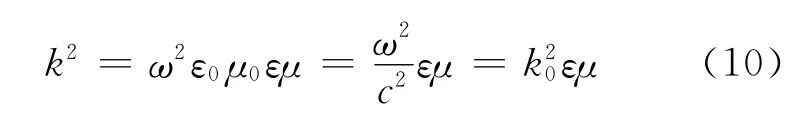
其中c为真空中的光速，为真空中波矢的模.相对折射率n按照下式定义

于是，由式（10）和（11），n可以写成

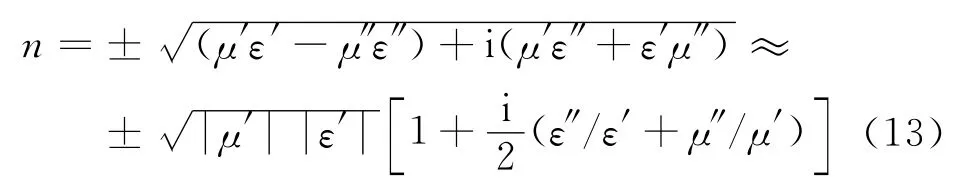
为保证n的虚部为正（否则违反因果律），式（13）正负号的选取是唯一的，于是Re（n）的正负号是确定的，即，

（1）当ε′＞0，μ′＞0时，上式应该取“＋”号，Re（n）＞0，对应正折射率材料情况；

（2）当ε′＜0，μ′＜0时，上式应该取“-”号，Re（n）＜0，对应负折射率材料情况.

于是，由式（11），折射率的正负决定k的正负.即，对负折射介质，Re（k）＜0.如果将介质损耗当作无穷小，则可以简单表述成：由于n＜0，所以k＜0，vph＝（ω／k）＜0，即相速度为负（注意默认了从波源指向观测者的方向为正方向）.

3 群速度

方程（1）虽然是满足麦克斯韦方程的特解，但实际电磁波不可能是绝对单频的，总是存在频率展宽，即实际上是由方程（1）那样的无穷多频率连续分布的特解的线性叠加.为简单起见，我们先考虑两个频率非常接近的单色平面波的叠加.假设第一个波的角频率和波矢分别为ω和k，第二个波为ω＋Δω和k＋Δk，假设两个场的振幅都是实数A，则叠加后总的电场为

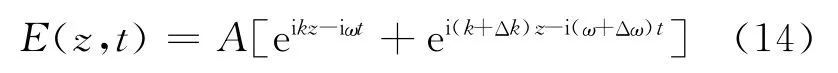
真实场应该对上式取实部，定义ER（z，t）＝ReE（z，t），有

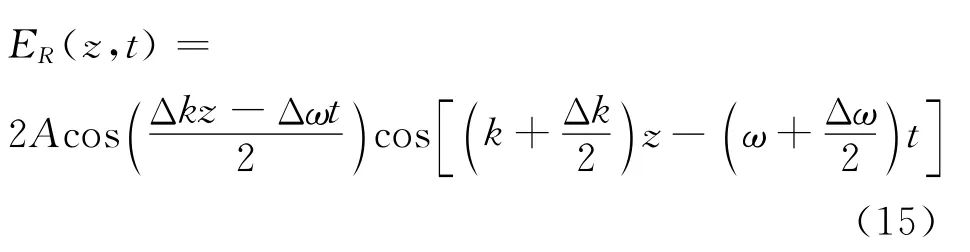
假设Δω≪ω和Δk≪k，则

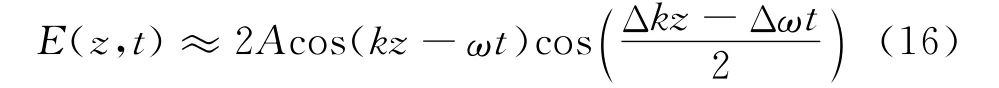
根据式（16），可知电磁场的运动是一个快变的振荡“cos（kz-ωt）”被一个慢变包络所调制.包络运动速度（即群速度）为Δω→0时，

我们也可以换个角度理解式（17）.考虑到光周期平均能量密度正比于｜E｜2，由式（14）可得

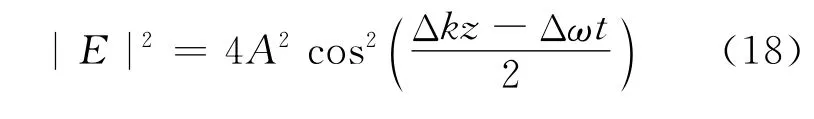
式（17）的推导只考虑了两个频率成分的叠加，实际中电磁波由无穷多连续分布的频率成分构成.根据傅里叶变换原理，可以证明：当频率展宽很窄时，慢变振幅中的“cos”函数将替换成一个非周期函数（代表电磁脉冲的包络），此时式（17）仍然成立[5].

由方程（17）的推导过程可知，它对波矢k为正和负值的情况均成立.对有色散的介质，群速度和相速度一般不等.由于波包的运动才代表真实的传播，所以式（17）给出的速度才是真实的传播速度.一般的介质中这两个速度尽管大小不等，但方向相同.然而，负折射材料中却不同，前面已通过分析表明负折射材料中波的相速度为负值，而式（18）表明群速度就是能量传递的速度，根据因果律，总是正值（图1）.群速度为正值也可以根据材料的色散关系k（ω）来证明，但考虑到需要借助于微观分析，较为复杂，下一节换用另一种方法，从能流密度（玻印亭矢量）角度分析，将发现负折射材料中相速度和能流传递的方向相反.

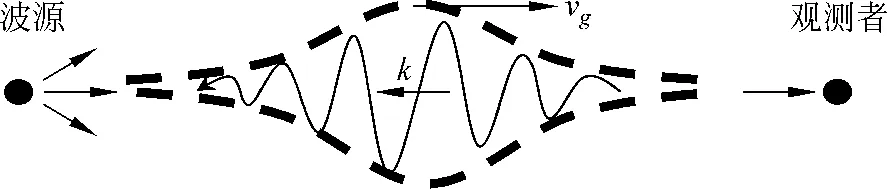
图1 负折射材料中群速度和相速度示意图

4 关于左手性的讨论

可以看到，若忽略吸收，则ε和μ均为实数.考虑ε和μ同时为正和同时为负两种情况（方程有传播解），下面通过证明：负折射材料中准单色电磁波的波矢k的方向与玻印亭矢量S的方向相反.

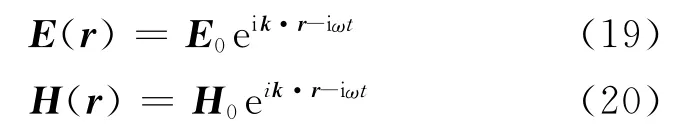
假设平面电磁波的表达形式为代入麦克斯韦方程组，可以得到

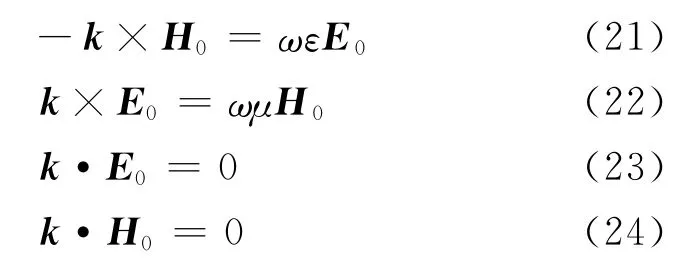
由式（3～6）4个方程可以看出，电场E、磁场H、波矢k三者的方向两两垂直.当ε＞0、μ＞0时，三者的方向满足右手螺旋关系；当ε＜0、μ＜0时，三者的方向符合左手螺旋关系，因此称为左手材料.

对传播解，玻印亭矢量的表达形式为[5]

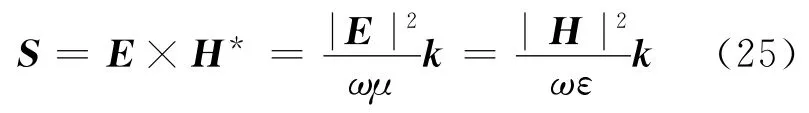
玻印亭矢量的定义决定了S、E、H三者总成右手螺旋关系.当ε＞0、μ＞0时，S、k方向相同，为前向波.当ε＜0、μ＜0时，S、k方向相反，为后向波（图2），这是负折射与正折射现象的最根本的差别.

5 电磁波在界面处的反射与折射

对各向同性的负折射率材料，忽略介质的吸收，根据电磁场边界条件，容易发现反射与折射定律仍然成立.根据电场E的切向（即沿界面方向）分量连续，得入射波、反射波、透射波的波矢的切向分量都相等[7]，设入射角为θi，反射角为θr，折射角为θt（图3），则

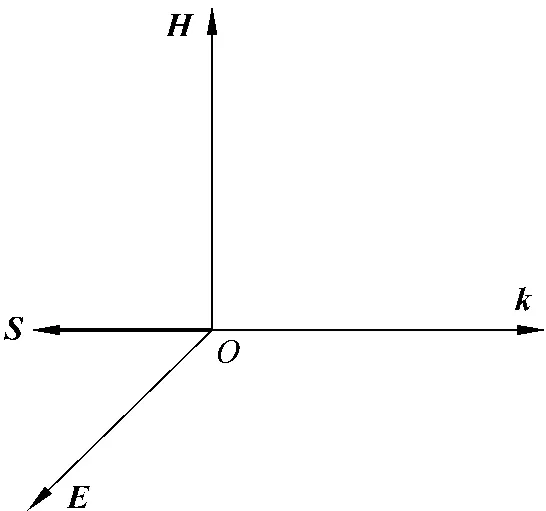
图2 负折射材料的左手性（E，H，k成左手系）

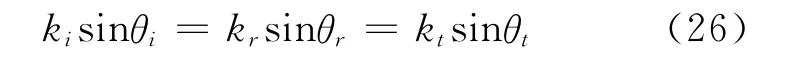
其中ki、kr、kt分别是入射、反射、折射波的波矢的大小，通常介质中它们都取正值，对负折射介质则取负值（代表相速度与能流方向相反）.由于入射和反射波在同一介质中，所以ki＝kr.假设电磁波从折射率为ni的介质进入折射率为nt的介质中，则

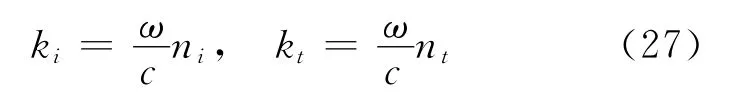
由式（26）得反射、折射定律如下

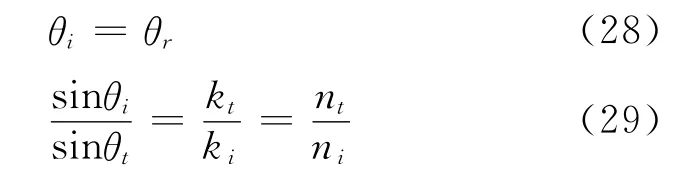
这与通常的反射、折射定律形式相同，只是折射率允许取负值.如果用“光线”描述光的传播方向，对通常两介质界面处的折射现象，入射和折射光线位于法线的两侧，而对两介质的折射率符号相反的情况，则折射与入射光线位于法线的同一侧.

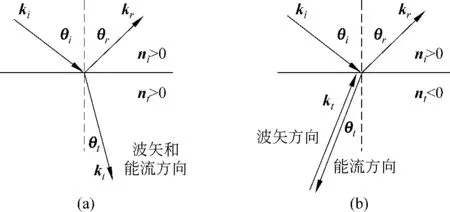
图3 反射、折射定律示意图

6 倏逝波放大

通过电磁场边界条件（E、H切向分量连续）可以导出电磁波在两个无限大介质交界面处的反射系数r与透射系数t，假设电磁波从介质i入射到介质t，两介质的相对介电常数和磁导率分别为（εi，μi）和（εt，μt），考虑 TE模式（电场E方向垂直于入射面），透射系数定义为反射系数定义为它们分别由以下方程给出[1，7]

其中kz、kz′分别代表入射和折射波的波矢在法线（z）方向的分量，注意到波矢的切向分量相等，有

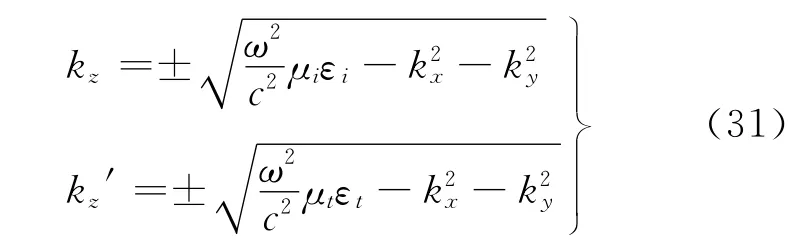
上式中的正负号的选取依据的原则与前面相同，即电磁波的电场E不能在无穷远处发散.假设介电常数和磁导率的虚部都很小（可以近似取为正无穷小量），若入射波满足条件则kz变成纯虚数，为倏逝波场.现通过一个特殊情况（即εi＞0，μi＞0，且εt＝-εi，μt＝-μi），分别讨论传播场和倏逝波场两种情况，从而表明倏逝场具有极不寻常的性质.

7 负介电常数和负磁导率的“微观起源”

介电常数ε和磁导率μ很容易被误认为是恒正的.对交变电场，由于介质的响应具有滞后性（极化强度P和电场E之间可能有相位差，磁化强度M和磁感应强度B之间也可能有相位差），它们实际上都有可能为负值.这一点我们从微观上分析.假设组成材料的电介质中的电子的运动可以简单描述成受电磁波驱动谐振子，其固有角频率为ω0，将能量耗散用阻尼系数为γe描述（γe＞0），它是吸收的起源.设电子有效质量为m，相对平衡位置的位移为r，在电场E的驱动下，有如下运动方程[7]

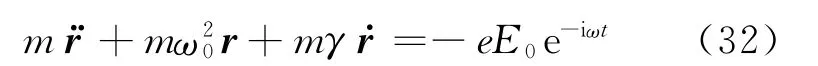
根据极化强度P＝ -Ner（N为电子数密度），及D＝ε0E＋P＝εE，可得相对介电常数

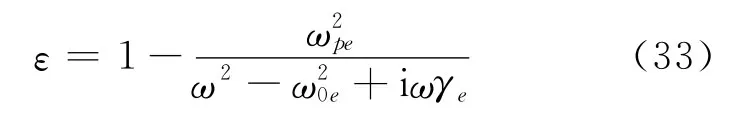
另一方面，考虑磁响应，可以类似给出相对磁导率

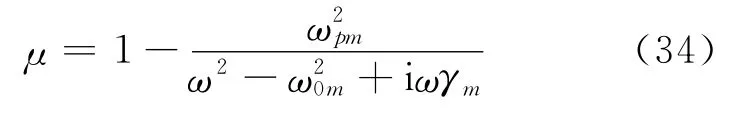
其中ωpm为磁响应等离子体角频率.式（33）与式（34）形式相同，也必然存在Reμ＜0的频段.忽略损耗的情况下，ε＜0和μ＜0两个频段的交集就是相对折射率n＜0的频段.这种材料在自然界中很难找到，但可以通过人工微结构组成的特异材料（metamaterial）来实现[4].

8 讨论

反思一下波动方程的求解，其中根据因果律舍弃了非物理解.其实这种做法在以往问题的分析中也是惯用的，例如量子力学中薛定谔方程的求解，也需要舍弃无穷远处发散的解，其原理是类似的，但值得深入思考.

从前面的分析不难看到，负折射现象是一类普遍存在的现象.实际上，负折射的研究已经不限于电磁现象，在声波、电子波、原子物质波等不同场合都存在.在声波的负折射方面已有不少实验报导[8，9].人们还发现电子波的负折射可以在石墨烯（graphene）材料中实现[10，11].另外，本文只给出了经典机制，实际上还存在量子机制，例如，材料的结构单元可以是超导量子电路[12].量子负折射材料中的新现象是另一个受到关注的新问题.另外，以上介电常数和磁导率同时为负的材料是产生负折射的一种可能方式，但不是唯一方式，还有可能通过其他方式产生，例如四波混频自相位共轭[13].

负折射现象具有普遍性，经典机制的负折射材料已经显示了大量新奇效应（例如在反常多普勒效应、反常切仑科夫辐射、超衍射极限的成像机制等）.由经典理论得到的新现象必然在量子理论中存在对应物，推广到量子领域可能有更多的新发展.

9 结语

本文探索性地用大学物理中的电磁学和波动理论简单解释了负折射现象.负折射现象使我们不得不重新思考关于波动方程的求解、相速度、群速度、能量传递和因果律、Snell定律等内容，以及电介质和磁介质的微观机制.这对更好掌握电磁学、光学以及一般波动理论都是大有帮助的.负折射理论可以用于课堂讲授，有利于增强经典物理教学内容的活力，激发学生探索新问题的兴趣；也可以与科研专题训练相结合，培养学生探索未知问题的能力.

我们从负折射现象可以得到一个启示：虽然我们对经典物理貌似很熟悉，但经典物理中仍然隐藏着被忽略的问题（负折射问题或许只是其中一个例子）.大学物理中关于电磁学、光学、波动理论等知识其实并不老，我们需要结合物理学新进展，不断地重新思考这些基础知识，有可能获得新的发现.

波动性是物质的一个最基本属性，在经典和量子理论中都扮演着极其重要的角色.经典物理中的问题往往更具普遍性，我们也许可以从这些问题入手，从新的角度重新思考包括量子物理在内的整个物理学，这在笔者看来是一个值得深入探索的问题.

[1]Pendry J B.Negative refraction makes a perfect lens[J].Phys.Rev.Lett.，2000，85（18）：3966-3969.

[2]Hau L V，Harris S E，Dutton Z D，et al.Light speed reduction to 17metres per second in an ultracold atomic gas[J].Nature（London），1999，397（6720）：594-598.

[3]Wang L J，Kuzmich A，Dogariu A.Gain-assisted superluminal light propagation[J].Nature，2000，406 （6793）：277-279.

[4]Smith D R，Pendry J B，Wiltshire M C K.Metamaterials and Negative Refravtive Index[J].Science，2004，305（5685）：788-792.

[5]Jackson J D.经典电动力学[M].3版.影印版.北京：高等教育出版社，2004.

[6]Raether H.Surface plasmons on smooth and rough surfaces and on gratings[M].Berlin：Springer-Verlag，1988.

[7]郭硕鸿.电动力学[M].北京：高等教育出版社，1979.

[8]Xie Y B，Bogdan-Ioan P，Zigoneanu L，et al.Measurement of a broadband negative index with space-coiling acoustic metamaterials[J].Phys.Rev.Lett.，2013，110（17）：175501.

[9]García-Chocano V M，Johan C，et al.Negative refraction and energy funneling by hyperbolic materials：An experimental demonstration in acoustics[J].Phys.Rev.Lett.，2014，112（14）：144301.

[10]Cheianov V V，Vladimir F，Altshuler B L.The focusing of electron flow and a Veselago lens in graphene p-n junctions[J].Science，2007，315（5816）：1252-1255.

[11]Cserti J，Pályi A，Péterfalvi C.Caustics due to a negative refractive index in circular graphene p-n junctions[J].Phys.Rev.Lett.，2007，99（24）：246801.

[12]Du C G，Chen H Y，Li S Q.Quantum left-handed metamaterial from superconducting quantum-interference devices[J].Phys.Rev.B，2006，74（11）：113105.

[13]Pendry J B.Time reversal and negative refraction[J].Science，2008，322（5898）：71-73.