空气阻力是滚摆能量损失的主要原因吗？

杨 景 侯吉旋

（1南京外国语学校，江苏 南京 210008；2东南大学 物理系，江苏 南京 211189）

物理学家一般习惯于将物理问题理想化之后再来处理，在基础物理课程之中尤为如此.然而，这样做会使得部分学生产生一种观点，就是物理课程与真实世界无关或者脱节.进一步的研究发现把真实情况和理想化后的情况同时介绍给学生会激发学生思考得更加全面[1].因此在课堂上多花一点时间来讨论如何改进物理模型是非常有益的.

图1 麦克斯韦滚摆示意图

在物理教学课堂中，麦克斯韦滚摆（见图1）经常被用来演示能量守恒[2].一般认为该系统的重力势能和动能来回转化并且总的机械能保持不变.但实际情况是滚摆每次都不能回到原来的高度，这是由于存在能量损失的缘故.我们相信合格的指导教师被问到此问题时并不会简单地将能量损失归因于空气阻力.除了空气阻力，在这个系统中确实存在多种能量损失的因素.让学生来找出各种能量损失的途径绝对不是一个平凡的练习，这样的练习可以让学生学习观察并且像物理学家一样思考.这也需要学生把有关于这个问题的各种因素（例如空气阻力、绳子的可伸缩性等）综合起来考虑，让学生整合各种知识点也是物理教育的一个重要目标.对于更高要求的基础物理课程，如果给学生一些相关的实验数据，学生应该可以做一些理论推演来估算各种效应的大小.

本文第1节将对无能量损失的麦克斯韦滚摆进行分析，然后在第2节考虑各种能量损失因素对该系统的影响.在第3节中，我们将用实验数据来分析哪一种能量损失因素占主导因素.结论和讨论将在最后一节中呈现.

1 无耗散的麦克斯韦滚摆系统

1.1 上升和下降

对于质量为m，中轴半径为r的滚摆，在上升或下降的过程中受力情况如图2所示.滚摆的运动满足方程

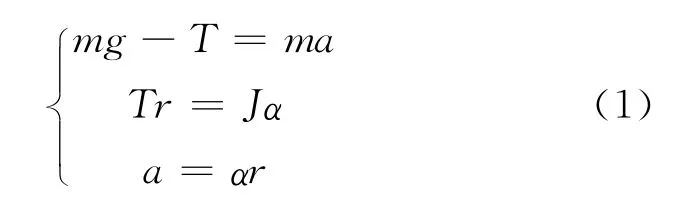
其中，J为滚摆绕中心轴转动的转动惯量；T为绳子的张力；a为滚摆的加速度；α为滚摆的角加速度.求解方程（1）得到

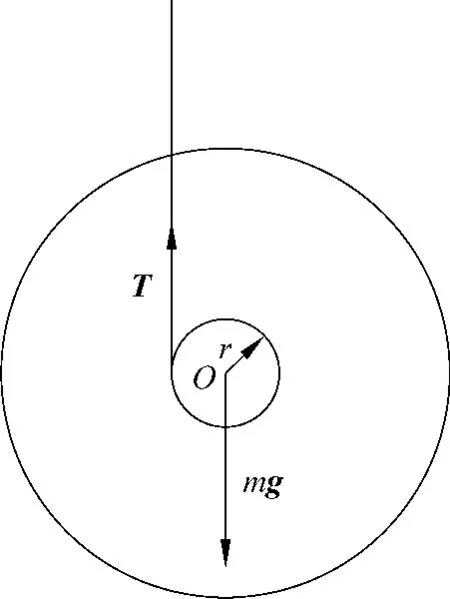
图2 滚摆在上升和下降过程中的受力分析图

对于一般滚摆来说，J≫mr2，因此绳子的拉力略微小于滚摆受到的重力.

1.2 最低点附近的运动

当绳子完全展开，绳子与滚摆的连接点O点将发生偏移，滚摆的运动将变得十分复杂.这里我们假定O点不动，因此在滚摆往复运动中运动轨迹是确定的，轨道是闭合的，如图3所示.当然这个假定并不符合实际，我们将在下一节对此进行更进一步的讨论.由于O点不动，滚摆的质心将作圆周运动，运动轨迹见图3（b）.如果滚摆开始滚动时质心的位置到O点的距离是h，根据式（2）可以求出当质心达到图3中A点时的速度为

图3 最低点附近质心的运动轨迹

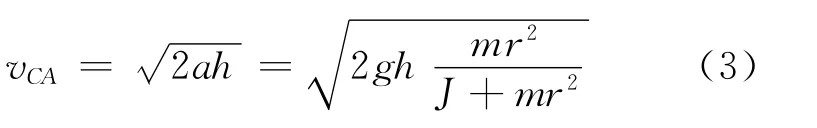
当质心达到最低点B点时，质心的速度vCB略大于vCA，不过由于h≫r，我们可以近似认为vCB≈vCA.因此当滚摆质心运动到最低点时，绳子张力T′的大小为

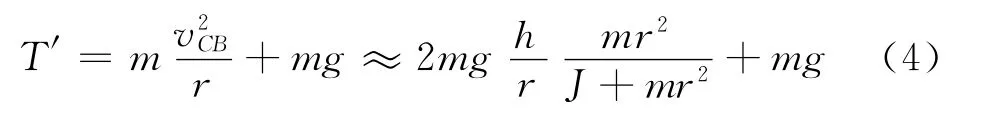
因此当滚摆质心运动到底部时，绳子张力变化量为

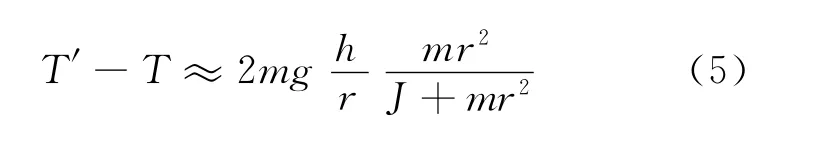
2 各种能量损耗

由于能量损耗的具体物理过程非常复杂，因此要完全定量地计算也非常复杂，我们在这里仅做半定量的讨论.

2.1 空气阻力

空气阻力的大小fg和物体相对于空气的运动速度v和形状有关.对于雷诺数很小的情形空气阻力的大小正比于速度的大小，一般实验用的单摆做小角度摆动时就属于这种情况，

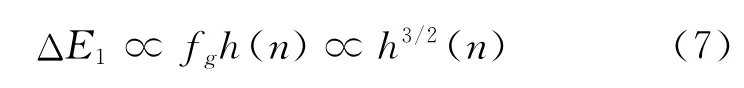
2.2 绳子的可伸缩性

文献[3]认为滚摆运动到最低点时，绳子张力迅速增大，由于实验中绳子不是完全刚性的，所以会带来额外的能量损失.假设绳子伸长正比于张力大小的变化量，根据式（5）有

由于绳子伸长并且将机械能转化成绳子的内能，则滚摆往复运动一次所损失的能量为

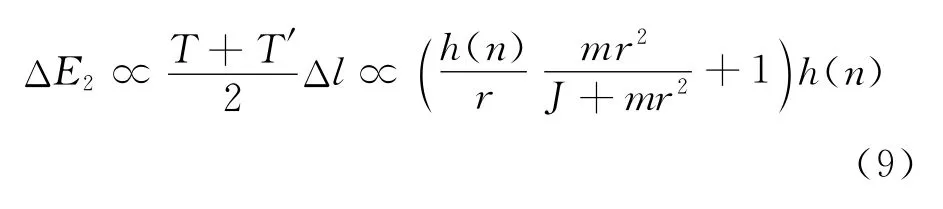
2.3 轨道不闭合

上一节中我们分析滚摆在最低点附近运动时，假设了绳子与滚摆的连接点O点不动.这个假设并不合理，因为O点会发生移动，如图4中（a）、（b）、（c）所示.从图4中我们可以看到，在A点时质心的速度是竖直方向的，在C点时质心的速度的方向变为水平，由于竖直的绳子无法提供水平方向的力，滚摆的轨道无法闭合，这样质心水平方向上平动的动能将传递到整个系统的绕悬挂点摆动自由度上（见图4（d））.因此，我们在做滚摆实验时，无论多么小心地进行操作，滚摆总是不可避免地绕着悬挂点摆动起来.

滚摆每次传递到其他自由度的能量可近似看成质心在最低点时的平动动能.根据公式（3），我们得到

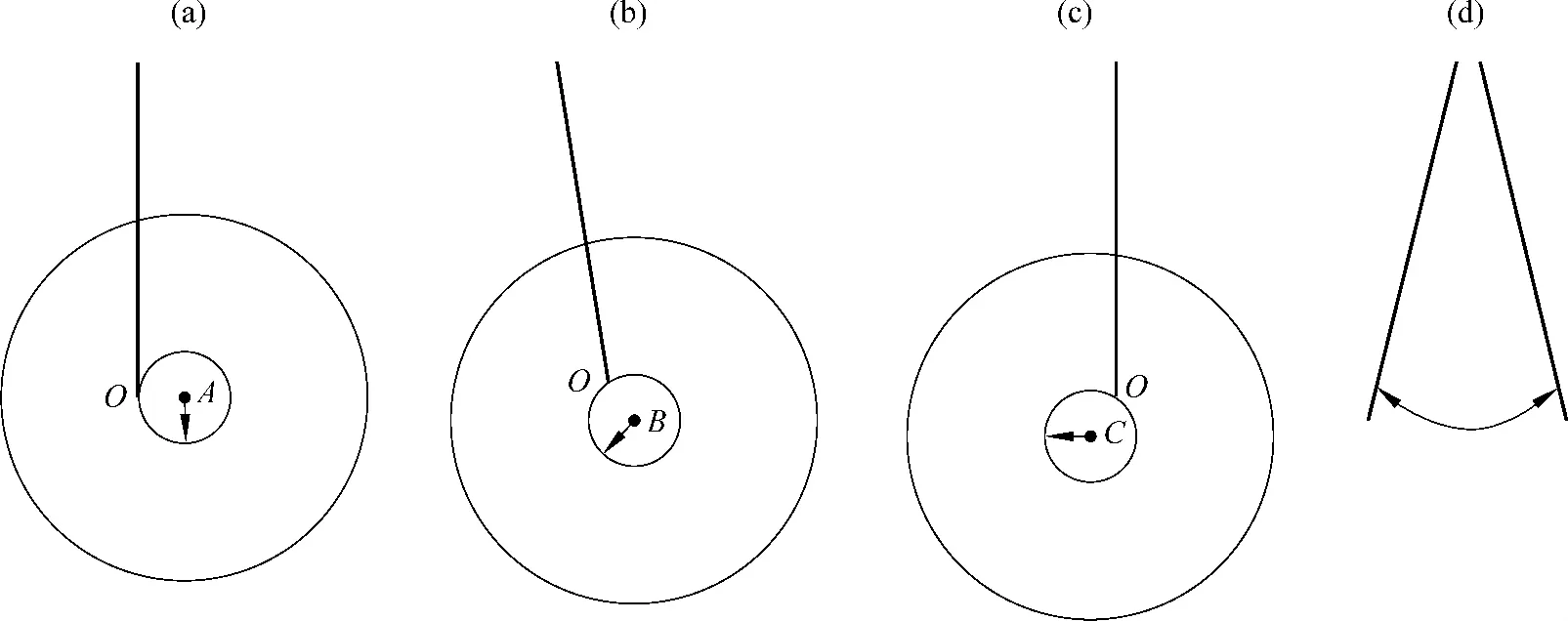
图4 滚摆在最低点时的运动示意图

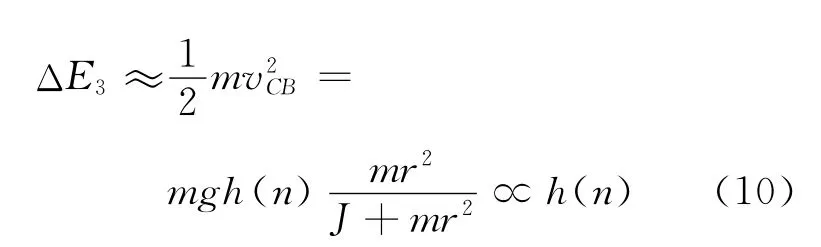
在这个过程中总的机械能并没有损失，而能量只是从一个自由度传递到了另一个自由度，于是滚摆就无法上升到原有高度.

综合上面各种因素，滚摆上下往复运动一次所损失的能量为ΔEtot＝ΔE1＋ΔE2＋ΔE3，因此根据式（7）、（9）、（10）最大高度的减小量可以写为

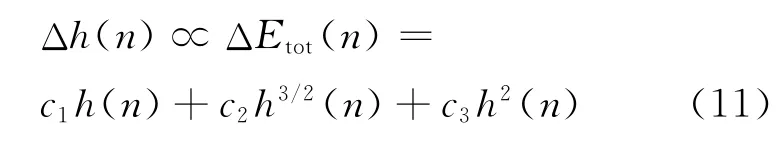
其中c1，c2，c3为非负常数.c2仅与空气阻力有关，c3仅与绳子伸缩性有关，c1则包含了绳子伸缩性和轨道不闭合两部分因素.

3 实验

我们选用3个用于课堂演示的麦克斯韦滚摆来进行实验.滚摆的质量和中轴的直径都可以直接测量.滚摆的转动惯量则只能通过间接方式测量得到.将滚摆从静止释放，测量滚摆向下运动20cm的距离所用的时间，就可以根据式（2）来算出转动惯量.3个滚摆的基本参数列在表1中.式（2）是在理想情况下推导出来的，但由此引起的误差不足以改变本文定性结果.

实验过程如下：将滚摆向上绕使质心升高一段距离（10cm和5cm），然后由静止开始释放，并记录之后滚摆质心每次上升的最大高度.我们的每个数据都是根据8次独立测量的平均值得到的，实验数据如图5所示.

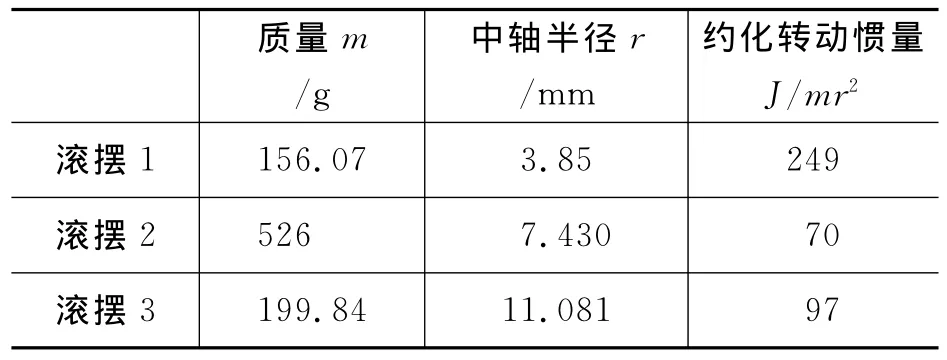
表1 3个滚摆的基本参数

图5显示滚摆每次上升的最大高度随上升次数单调减小，但是并不能提供更多的关于能量损失的信息.为了分析哪种能量耗散占主导地位，我们按照式（11）处理我们的数据，结果显示在图6中.其中式（11）中的Δh（n）我们用差分[h（n＋1）-h（n-1）]／2来表示.

图6显示Δh（n）与h（n）几乎是线性关系，说明在误差范围内式（11）中c2与c3约等于零.按照式（11），非线性部分c2是由空气阻力给出的，如果空气阻力是能量损失的主要原因，那么图6将呈现明显的非线性.由图6显示的线性关系，可以判断在测量误差范围内空气阻力造成的能量损失在滚摆竖直方向上振荡的能量损耗中必然只占极小部分.

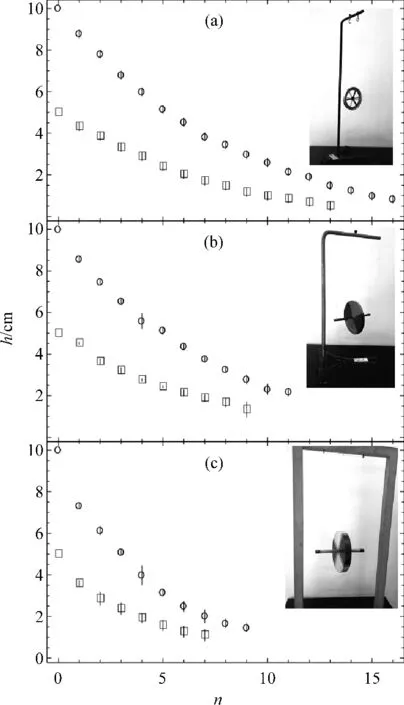
图5 滚摆每次上升的最大高度

图6 滚摆损失的高度与最大高度之间的关系

4 结果和讨论

我们首先分析了理想的麦克斯韦滚摆的物理过程，然后半定量地分析了麦克斯韦滚摆系统中各种能量损失的物理原因，包括（1）空气阻力、（2）绳子的可伸缩性和（3）轨道不闭合.通过测量麦克斯韦滚摆每次上升高度的变化，可以推断出空气阻力不是能量损失的主要原因.根据我们的实验数据，还无法推断绳子的可伸缩性和轨道不闭合哪一个是滚摆竖直方向上振荡的能量损耗的主要原因.

本文潜在的教学价值在于教育学生如何从有限的数据中挖掘出需要的信息.例如在研究空气阻力对麦克斯韦滚摆的影响时，当然可以将滚摆置于真空与非真空条件下做对比性实验，从而判断是非.然而在没有大型的真空装置的条件下，此法难以实现.本文却给出了现实可行的方法.

[1]Veronica C M，Butler P H，Undergraduate students’under-standing of falling bodies in idealized and real-world situations[J].Journal of Research in Science Teaching，2004，41（6）：569-583.

[2]Naimi E K，The Maxwell pendulum [J].Soviet Physics Journal，1979，22（11）：1225-1227.

[3]周雨青，刘甦，机械能守恒演示中一个值得商榷的案例“悠悠球”系统能量损失分析[J].大学物理，2011，30（8）：18-21，2011.