基于超声导波技术的双层粘接结构界面质量检测

吴慧 李晓高 沈国浪 王兴国 马成文

摘要：

针对粘接结构界面质量难以检测的问题，提出一种超声导波检测技术方法。基于弹簧模型和波动方程建立超声导波在双層粘接结构中传播的数学模型，获得不同粘接界面的频散方程，通过求解该方程获得不同粘接界面的频散特性。利用COMSOL软件模拟了声波在不同粘接界面的传播过程。仿真结果表明，在频率为1 MHz时刚性粘接条件下，数值求解的群速度为4.632 km/s，仿真平均群速度为4.505 km/s，误差为2.74%；在滑移粘接条件下，数值求解的群速度为4.855 km/s，仿真平均群速度为5.045 km/s，误差为3.91%；在完全脱粘条件下，双层粘接结构频散曲线为单层频散曲线的叠加。通过对双层介质超声导波实验检测结果的分析，发现实验结果与数值求解和有限元仿真结果吻合较好，验证了该理论模型的正确性。

关键词：粘接结构；弹簧模型；频散方程；有限元仿真；群速度

中图分类号：TB553

DOI：10.3969/j.issn.1004132X.2024.05.017

开放科学（资源服务）标识码（OSID）：

Interface Quality Detection of Double-layer Bonding Structures Based on

Ultrasonic Guided Wave Technology

WU Hui  LI Xiaogao  SHEN Guolang  WANG Xinguo  MA Chenwen

School of Mechanical and Electronic Engineering，Jingdezhen Ceramic University，Jingdezhen，

Jiangxi，333403

Abstract： A ultrasonic guided wave detection method was proposed to address the difficulty in detecting the interface quality of adhesive structures. Based on the spring model and wave equation， the mathematical model of ultrasonic guided wave propagation in the double-layer bonding structure was established， and the dispersion equations of different bonding interfaces were obtained. The dispersion characteristics of different bonding interfaces were obtained by solving the equations. The propagation processes of sound waves at different adhesive interfaces were simulated using COMSOL software. The simulation results show that under the condition of 1 MHz frequency rigid bonding， the group velocity numerically solved is as 4.632 km/s， and the simulated mean group velocity is as 4.505 km/s， with error of 2.74%. Under the condition of slip bonding， the numerical solution group velocity is as 4.855 km/s， and the simulation mean group velocity is as 5.045 km/s， with error of 3.91%. Under the condition of complete debonding， the dispersion curve of the double-layer adhesive structure is the superposition of the single-layer dispersion curve. Through the analysis of the experimental detection results of ultrasonic guided waves in double-layer media， it is found that the experimental results are in good agreement with the numerical solution and finite element simulation ones， which verifies the correctness of the theoretical model.

Key words： bonded structure; spring model; dispersion equation; finite element simulation; group velocity

收稿日期：20230509

基金项目：国家自然科学基金（52265020）；江西省教育厅项目（7201020102）

0  引言

粘接结构具有强度高、刚度高、成本低、比模量高等特点，被广泛应用于航空航天、精密器械、军工制造等领域［1-3］。但在制备加工过程中，粘接不良、局部脱粘等缺陷会破坏粘接结构的完整性，从而导致一些重大安全事故的发生［4-6］，因此，对多层结构界面粘接特性的检测与评价就显得尤为重要。

超声无损检测被普遍认为是一种评价粘接界面质量的有效方法［7-8］，因其具有安全无辐射、穿透能力强等优点，可以较好地检测界面脱粘、宏观缺陷和胶层厚度，已成为检测粘接界面特性的重要手段之一［9-12］。与传统超声检测方法不同，超声导波检测具有传播距离远、检测范围广、检测频率较低和灵敏度较高等优点［13-15］，因此，超声导波检测方法广泛应用于各个领域，是一种发展前景广阔的无损检测技术［16-17］。

目前，国内外已有学者运用多种不同的超声导波检测方法研究了粘接结构的界面特性。在线性超声导波检测方面，MEI等［18］提出了一种新的单模导波航空复合材料损伤检测方法实现单模导波激励，通过理论、有限元仿真以及实验相互验证，以检测各种类型的复合材料损伤。KOODALIL等［19］利用剪切水平导波评估了不同粘接强度的剪切接头，发现接头粘接强度对一阶SH1模态的频散特性影响最大，提出了利用SH1波在剪切接头中传播的时间来判断粘接质量的方法。张超等［20］利用传递矩阵推导了双层和多层粘接结构模型中的频散方程，通过对频散方程数值求解，发现双层结构基阶模态高频极限等于瑞利波波速，高阶模态高频极限等于横波波速。吕瑞宏等［21］建立了非线性超声导波在微体元结构中的传播模型，通过回波信号对管道不同粘接状态的材料参数进行分析，结果表明，回波信号的最大幅值与信号能量具有一致性，当粘接结构存在缺陷时，信号能量介于完好粘接与弱粘接之间。SONG等［22］提出了一种基于导波衰减特性的空气耦合超声无损评价方法，利用整体矩阵技术得到了各种粘接界面条件下的导波模态解析解，通过数值模拟与实验相结合验证了对称（S0）导波模式的衰减特性对界面粘接特性敏感。ROKHLIN等［23］从理论和实验两方面展示了如何选择关节外Lamb波激发模式类型和频率，以在关节区域获得合适的模式，从而成功区分粘接质量。王兴国等［24］提出一种空气耦合超声检测方法，推导出了双层介质中的频散方程，通过数值模拟与实验相互验证，表明在A0模态的一定频率范围内，界面趋于刚性粘接时，导波的传播相速度大于滑移粘接的相速度。杨理践等［25］利用压电超声对管道防腐层进行检测的方法研究了超声波在双层介质中的传播特性，结果表明超声兰姆波在覆有破損防腐层比覆有完好防腐层的钢板中传播速度快、衰减慢。

综上所述，超声导波技术不但可以检测粘接结构的界面特性，还可以检测粘接结构内部微裂纹损伤、复合材料冲击损伤，以及被测界面的疲劳损伤程度等，因此，该技术对粘接结构的界面状态以及检测各种损伤有很大的应用潜力。由于导波本身具有检测距离长、检测范围广等优势，给实际检测提供了便利，但是导波具有多模态性，以及需要满足一定的检测参数才可以激励相应的模态且存在信号接收较弱等问题，因此在导波试验方法的改进、模态信号的提取等方面有很大的研究空间。本文结合波动方程与传递矩阵方法建立了双层板的传递矩阵数学频散方程，通过对频散方程的数值求解获得导波在层状介质中的频散曲线，再分析不同界面粘接状态下的频散特性。基于COMSOL有限元建立仿真模型搭建超声导波检测实验平台，验证了刚性粘接与滑移粘接频散曲线模态的群速度匹配，双层板完全脱粘的频散曲线为单层板频散曲线的叠加。这为利用超声导波技术分析层状介质中的界面粘接特性提供了一定的理论基础。

1  双层介质粘接结构超声导波模型

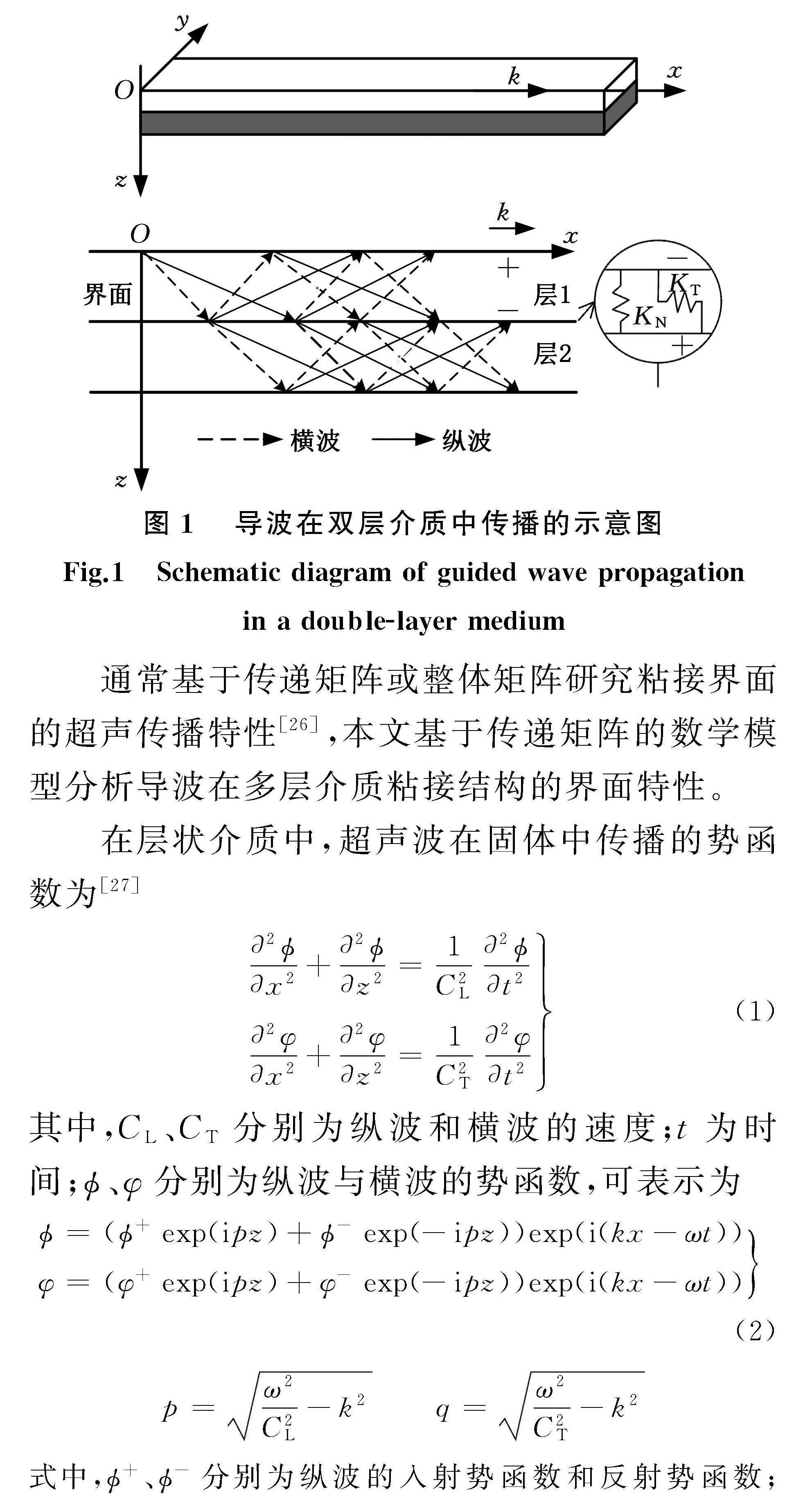
图1为导波在双层介质中传播的示意图。直角坐标系原点O位于超声波发射点，x、z为坐标轴，x向右为正，z向下为正，k为波数，其方向为声波传播方向，“+”、“-”分别表示层的上下表面，KN、KT分别为粘接界面的法向刚度系数和切向刚度系数。

通常基于传递矩阵或整体矩阵研究粘接界面的超声传播特性［26］，本文基于传递矩阵的数学模型分析导波在多层介质粘接结构的界面特性。

在层状介质中，超声波在固体中传播的势函数为［27］

2x2+2z2=1C2L2t22φx2+2φz2=1C2T2φt2（1）

其中，CL、CT分别为纵波和横波的速度；t为时间；、φ分别为纵波与横波的势函数，可表示为

=（+exp（ipz）+－exp（－ipz））exp（i（kx－ωt））

φ=（φ+exp（ipz）+φ－exp（－ipz））exp（i（kx－ωt））（2）

p=ω2C2L－k2  q=ω2C2T－k2

式中，+、-分别为纵波的入射势函数和反射势函数；φ+、φ-分别为横波的入射势函数和反射势函数；i为虚数；ω为角频率。

由平面应变假设可知，位移分量ux和uz、应力分量σx和σz分别为［27］

ux=ik+dφdz

uz=ddz－ikφ

σx=μ（2ikddz+k2φ+d2φdz2）

σz=λ（－ik2+d2dz2）+2μ（d2dz2－ikdφdz）（3）

将式（2）代入式（3）可得

uxuzσxσz=DE+－φ+φ－（4）

D=

1111α2－1－α2－1β2－1－β2－1μ（α2－2）μ（α2－2）－2μ－2μ2μα2－1－2μα2－1μ（α2－2）β2－1－μ（α2－2）β2－1

E=diag

（exp（izkα2－1），exp（－izkα2－1），

exp（izkβ2－1），exp（－izkβ2－1））

α=Cp/（λ+2μ）/ρ  β=Cp/μ/ρ

k=2πf/Cp

式中，Cp为导波的相速度；λ、μ分别为梅拉常数的第一参数和第二参数；ρ为上层介质的密度；f为超声波的频率。

层1上下表面的位移u和应力σ边界条件为

u－x（1）=u+x（2）u－z（1）=u+z（2）σ－x（1）=σ+x（2）σ－z（1）=σ+z（2）（5）

其中，下标数字1、2分别表示层1和层2，上标“+”、“-”分别表示上表面和下表面，则第一层传递矩阵

L1=D1u×D－11d（6）

同理，可得第二层传递矩阵

L2=D2u×D－12d（7）

其中，L1为第一层介质矩阵，L2为第二层介质矩阵，D1，u为第一层介质上表面矩阵，D1，d为第一层介质下表面矩阵，D2，u为第二层介质上表面矩阵，D2，d为第二层介质下表面矩阵。在理想粘接条件下，各层之间界面上的应力和位移都是相等的，因此有

D－11d=D2u（8）

联立式（6）～式（8），可得到双层理想粘接界面结构的传递矩阵

S=L1L2（9）

当粘接结构的两个界面都满足自由边界条件时，可知第一层上表面和第二层下表面的边界条件是切向应力和法向应力都为零，联立式（4）和式（9）可得理想粘接条件下双层粘接结构的频散方程

F（CL，CT，ρ，d，f，CP）=S3×1×S4×2－S4×1×S3×2=0（10）

其中，S下标中“×”前后数字分别表示矩阵S的行和列，d为双层板的厚度。

当出现滑移粘接和完全脱粘条件时，粘接结构分为上下两层，其传递矩阵可分别表示为Su和Sd，利用弹簧模型模拟两层板之间的粘接特性，则弹簧模型可表示为

σ－x（1）=σ+x（2）

σ－x（2）=KT（u－x（1）－u+x（2））

σ－z（1）=σ+z（2）

σ－z（2）=KN（u－z（1）－u+z（2））（11）

通过改变法向刚度系数KN和切向刚度系数KT模拟不同的界面粘接特性。式（11）经变换后可得

u－x（1）u－z（1）σ－z（1）σ－x（1）=1001KT011KN000100001u+x（2）u+z（2）σ+z（2）σ+x（2）（12）

联立式（10）、式（12）可得

F（CL，CT，ρ，d，f，CP，KT，KN）=

Su1001KT011KN000100001Sd=0（13）

式（13）即為不同粘接界面刚度的数学频散方程。

2  双层介质频散曲线数值求解

式（13）为复数非线性超越方程，f和Cp难以直接求解，但可应用MATLAB软件采用五点二分法求解，并通过弹簧模型模拟界面的粘接程度。现以有机玻璃和铝板为研究对象，通过求解频散方程，可获得刚性粘接、滑移粘接和完全脱粘三种粘接状态的频散曲线，见图2。其中，有机玻璃铝板双层介质的声学参数和表征不同界面的刚度系数分别如表1和表2所示。表2中符号∞以1015表示。图2a、图2b和图2c分别给出了刚性粘接、滑移粘接、完全脱粘时有机玻璃板与铝板

频散曲线，其中A0～A2、S0～S2表示模态。

由图2可以看出，不论是刚性粘接还是滑移粘接，最终频散曲线都会收敛于某一特定的数值。而当模态的阶数高于基阶（A0，S0）时，在特定的

频率下会出现一些特殊的点，在这些点中相速度趋于无限大，群速度趋于0。图3a、图3b为分别对单层铝板和单层有机玻璃板进行数值求解而绘制的频散曲线图，对比图2c与图3可以得出双层介质完全脱粘频散曲线是有机玻璃板与铝板两个单层板频散曲线的叠加。这是由于声波在板中发生反射而无透射，因此频散曲线上会出现两种相同模态的频散曲线，黑色线是有机玻璃频散曲线，红色线是铝板层的频散曲线。而双层板数值求解计算的结果也是有机玻璃和铝板两种曲线的叠加，这在后续的仿真求解结果中也可以得到验证。

3  双层粘接结构有限元模拟分析

3.1  双层粘接结构几何模型

采用COMSOL软件的声压电相互作用模块搭建有机玻璃板铝板二维平面结构模型，如图4所示。该模型由超声传感器、空气域、有机玻璃板、铝板以及粘接层组成，其中有机玻璃板、铝板以及粘接层的参数如表3所示。该模型中，刚性粘接的有机玻璃铝板中间为环氧树脂胶薄层，滑移粘接的有机玻璃铝板中间为水薄层；完全脱粘的有机玻璃铝板中间为空气薄层。超声传感器与板材之间的夹角为θ，由Snell定律可知θ可由下式确定［21］：

sin θ=CLaCp（14）

式中，CLa为声波在空气中的纵波声速。

3.2  双层粘接结构有限元模型仿真

本文仿真所采用的传感器中心频率分别为1 MHz、1.2 MHz，在这两种频率下频散曲线模态易区分，接收到的信号更加准确，检测到的精度更高［24］。在刚性条件下均将产生A0、S0、A1、S1四种模态的波；滑移粘接条件下均将产生A0、S0、A1、S1、A2五种模态的波；完全脱粘条件下铝板会产生A0、S0两种模态的波，有机玻璃会产生A0、S0、A1三种模态的波。本文选取的激励模态能够传播较长的距离，而且群速度相对较高，这可使与其他模态相区别，易于识别［28］。相速度Cp与群速度Cg的转化公式如下：

Cg=C2p［Cp-（fd）dCpd（fd）］-1（15）

由式（15）可求出两种频率下三种粘接状态所对应模态的群速度［2］，其理论计算结果表4所示。

3.2.1  刚性粘接条件下的群速度测量

双层结构刚性粘接的有机玻璃板与铝板高度均设定为1 mm，选取不同的检测距离X进行仿真计算。根据式（14）可求出在频率为1 MHz和1.2 MHz条件下入射角度分别为3.65°和3.78°，再通过测量不同的检测距离，从而根据仿真波形图的波峰时间计算出导波传播群速度。刚性粘接条件下不同检测距离X的波形如图5所示。

通过理论计算可得出在刚性粘接条件下，频率为1 MHz时S1模态的群速度为4.632 km/s，再提取S1模态下的波形进行计算，可得到刚性粘接条件下在不同检测距离时S1模态的群速度；同理可得到频率为1.2 MHz时不同检测距离下的群速度。综合表5（表中距离ΔX为对检测距离

X转化的相对距离）给出的结果可知，理论结果与仿真结果相比误差在10%范围内。

3.2.2  滑移粘接条件下的群速度测量

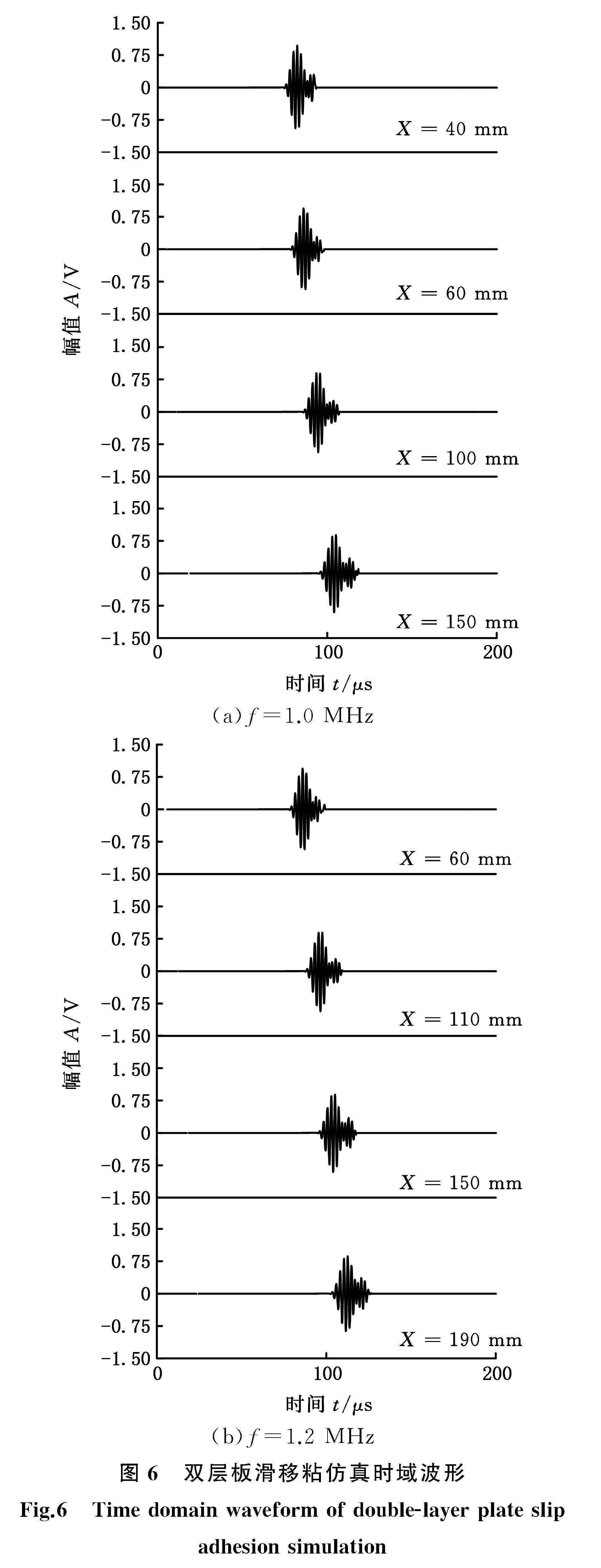
为了验证滑移粘接状态下频散曲线中群速度匹配，与刚性粘接条件下相似，通过对滑移粘接双层结构的频散曲线进行分析可以求解出频率为1 MHz和1.2 MHz时各自模态的群速度，从而构建滑移粘接状态下的仿真模型。相比于刚性粘接，滑移粘接只是将粘接剂环氧树脂层换成水层来模拟滑移状态，法向刚度系数无限大，切向刚度系数为零。分别在不同检测距离X下接收超声信号，双层板滑移粘接条件下的仿真时域波形如图6所示。

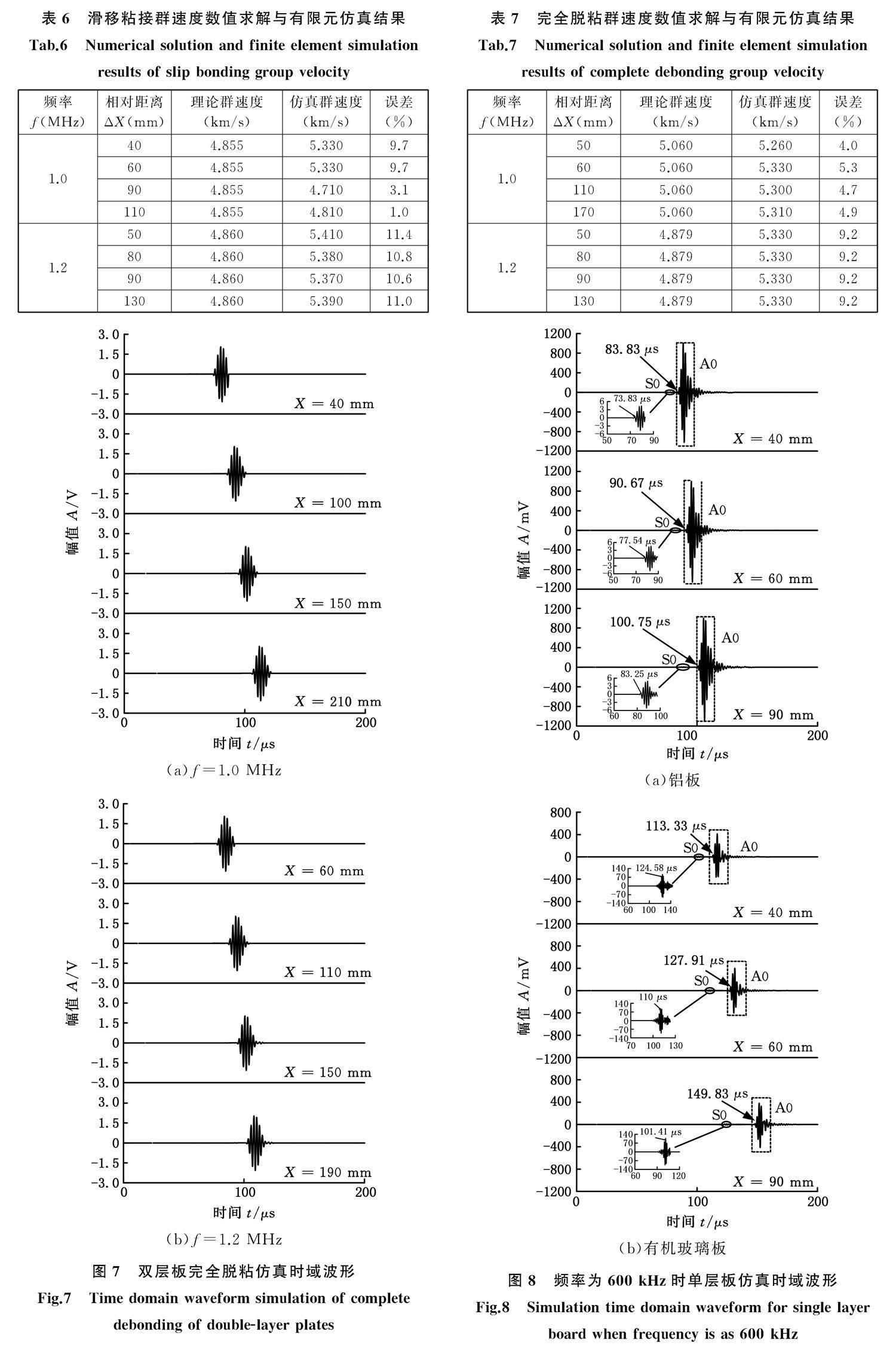
通过理论计算可得出在滑移粘接条件下，频率为1 MHz时激发A2模态的群速度为4.855 km/s，提取A2模态下的波形图可计算获得不同距离下A2模态的群速度；同理可测出频率为1.2 MHz时的群速度，见表6。从表6中可以看出，当激励频率为1 MHz时，理論群速度与仿真群速度的误差较小，最小仅为3.1%；当频率为1.2 MHz时，两者误差较大，均在10%左右。

3.2.3  完全脱粘条件下的群速度测量

图7给出了完全脱粘双层结构的时域波形，可以看出，随着检测距离的增大波形整体会逐渐后移。完全脱粘条件下的数值求解群速度与仿真计算群速度如表7所示，其中频率为1 MHz时最大误差为5.3%，最小误差为4%；频率为1.2 MHz时误差均为9.2%。

接下来利用有限元方法仿真分析单层铝板和单层有机玻璃板的导波传播特性。传感器的中心频率分别取400，600，800 kHz，其中选取频率为600 kHz时进行仿真，结果如图8所示，图中将S0模态的波形图进行放大便于观测，其中S0模态所对应的波型在前，A0模态所对应的波型在后，这是由于频率为600 kHz时，S0模态的群速度较大，A0模态的群速度较小。

通过提取图8所示仿真时域波形给出的到达时间，计算频率分别为400，600，800 kHz时的有限元模拟群速度，再与数值求解得到的群速度进行对比分析，可知单层有机玻璃板与铝板的数值求解群速度与有限元仿真群速度误差均较小，最大为6.8%，最小仅为0.3%，如表8所示。该结果也证明了有机玻璃板与铝板双层结构完全脱粘的频散曲线是由它们各自的频散曲线组成的。

4  实验

4.1  设备及方法

图9所示为双层板超声导波实验装置，其中上层为1 mm厚的有机玻璃板，下层为1 mm厚的铝板。刚性粘接以环氧树脂为胶粘剂并且将刚制作好的双层板放在恒温恒压条件下固化24 h后使用；滑移粘接以水为胶粘剂，当两块板之间均匀分布水时需用力挤压尽可能将空气排出；完全脱粘将两块板直接接触不做任何处理。实验在刚性粘接和滑移粘接条件下采用一对1 MHz的传感器，一个传感器作为发射端，另一个作为接收端并且保持发射传感器位置不变，通过移动接收楔块的位置从而控制相对距离以达到对群速度测量的目的，再通过控制超声检测软件触发脉冲发射/接收装置（型号 JPR-10CN）产生脉冲信号激励发射传感器，然后由另一端传感器接收，最后由脉冲发射/接收装置将收到的信号送至计算机保存并记录。

通过移动超声传感器的位置获取相对位移，再测量两次传感器位置所对应导波波峰的时间差从而计算出导波传播速度。为了提高测量精度，设置多个测量距离，将计算导波速度的平均值作为最后的实验结果。图10为双层板超声导波实验示意图。保持发射超声传感器位置不变，用刻度尺记录位置信息，然后改变测量位置，获取不同位置下的时域信号。

4.2  实验结果与讨论

采用有机玻璃斜楔块放置超声传感器进行发射与接收，研究导波在粘接结构中的传播。以群速度为检测参量，通过测量楔块的位移并记录对应的时间来计算群速度。声波在楔块中的传播在本次实验中不作考虑。

从刚性粘接的频散曲线中可以看出，频率为1 MHz时S1模态时的相速度Cp为5.34 km/s。根据Snell定律可求出刚性粘接条件下的角度为30°，为了计算双层板中产生的单模波群速度，从实验中提取4个不同位置的波形如图11a所示。滑移粘接条件下，1 MHz频率下的频散曲线显示A2模态的相速度最大，曲线相对平滑，这也导致群速度最大，从而最先观测到A2模态的波型，因此选取A2作为超声检测激励模态。同样与刚性粘接一样，在1 MHz频率下求解出滑移粘接条件下导波相速度为5.36 km/s，根据Snell定律求解出角度为30°，并通过实验得到该条件下的波形，如图11b所示。完全脱粘条件下，频散曲线可以认为是有机玻璃板与铝板的频散曲线的叠加，所以在频散曲线上会有两种相同的模态产生。在完全脱粘状态下，只需要研究单层板。在1 MHz频率下铝板的模态高、群速度大，更易于观测，所以本文选取1 mm厚的铝板进行实验，实验结果如图11c所示。

群速度Cg的计算公式为

Cg=ΔXΔt（16）

其中，ΔX为传感器之间的移动距离；Δt为2个波包峰值时间差。根据式（16）可以计算出1 MHz频率下在不同检测距离时刚性粘接、滑移粘接和完全脱粘状态下的群速度，具体结果见表9。从表9中可以看出，三种粘接状态下的实验群速度与数值求解的群速度之间的误差均较小。

通过对刚性粘接、滑移粘接以及完全脱粘条件下的不同检测距离进行多次测量，计算出平均群速度，再将检测距离所对应的平均群速度绘制出误差棒，如图12所示，可以看出刚性粘接下的误差最大，滑移粘接与完全脱粘次之，误差均在10%范围内。

图13给出了不同检测距离与导波幅值的关系。通过实验获得的波形可以获取导波幅值。随着检测距离的增大，导波传播的时间增加，幅值减小，这是由于检测距离增大而导致声波能量衰减，这也符合超声传播特性。由图13可知，完全脱粘的幅值最大，刚性粘接幅值最小，这是由于刚性粘接时粘接层近似于理想界面，声能量的传递遵循界面声压分配原则，导致超声导波穿透双层结构后反射能量降低、幅值小；完全脱粘时的粘接程度最差，可以看作为界面出现一层薄薄的空气层，声能量不能够透射到下层板，仅在上层板发生全反射，因此超声导波检测双层脱粘结构时幅值最大，能量最高。

频率为1 MHz时对刚性粘接、滑移粘接、完全脱粘三种粘接状态进行数值求解、有限元仿真以及实验研究，将有限元仿真与实验得到的群速度取平均值并列于表10，通过计算可得，刚性粘接与完全脱粘下的误差均较小，最大误差仅为5.2%，最小误差为0.3%；滑移粘接下的误差较大为10%。这与有限元仿真误差结果相似。

5  结论

本文提出一种基于超声导波技术的界面特性检测方法，建立不同粘接界面的频散方程，利用仿真与实验手段研究了刚性粘接、滑移粘结、完全脱粘条件下频散曲线的特性，具体结果如下：

（1）在激励频率为1 MHz、1.2 MHz时，分别对刚性粘接、滑移粘接、完全脫粘三种粘接状态进行有限元仿真，数值求解结果与有限元仿真结果相比，刚性粘接群速度最大误差为5.5%，最小误差为1.6%；滑移粘接最大误差为11.4%，最小误差为1%；完全脱粘条件下，最大误差为9.2%，最小误差为4%。数值求解结果与仿真结果一致性较好，验证了双层粘接频散数学模型的正确性。

（2）在完全脱粘条件下，分别选取400，600，800 kHz三种不同频率条件下对单层铝板与单层有机玻璃板进行有限元仿真，单层铝板群速度最大误差为6.5%，最小误差为0.3%；单层有机玻璃板群速度最大误差6.8%，最小误差为0.8%。该结果表明铝板与单层有机玻璃双层结构完全脱粘的双层板频散曲线为两个单层板频散曲线的叠加。

（3）在刚性粘接、滑移粘接、完全脱粘条件下，频率为1 MHz时数值求解、有限元仿真与实验结果获得的群速度最大误差为10%，最小误差为0.3%，数值求解、有限元仿真与实验结果基本吻合，验证了在单一频率下三种频散曲线的正确性。

参考文献：

［1］  敦怡，师小红，徐章遂.非线性超声在金属基复合材料结构界面粘接强度评价中的应用［J］.中国机械工程， 2008，19（19）：2351-2354.

DUN Yi，SHI Xiaohong，XU Zhangsui. Nondestructive Evaluation of Adhesive Interfaces in MMCS Using Nonlinear Ultrasonic Method［J］. China Mechanical Engineering，2008， 19（19）：2351-2354.

［2］  黄辉， 许波， 励柳波，等. 非接触空气耦合兰姆波的薄板检测技术及应用研究［C］∥2013远东无损检测新技术论坛.济南，2013：115-122.

HUANG Hui，XU Bo，LI Liubo，et al. Research of Non-contact Air Coupled Lamb Wave Testing for plate testing and application［C］∥2013 Far East Nondestructive Testing New Technology Forum. Jinan，2013：115-122.

［3］  罗元国， 王保良， 黄志尧，等. 空气耦合式超声波无损检测技术的发展及展望［J］. 仪器仪表学报， 2005，26（8）：742-744.

LUO Yuanguo， WANG Baoliang， HUANG Zhiyao， et al. Progress and Prospect of Air-coupled Ultrasonic Non-destructive Evaluation［J］. Chinese Journal of Scientific Instrument. 2005，26（8）：742-744.

［4］  MUNIAN R K， MAHAPATRA D R， GOPALA-KRISHNAN S. Lamb Wave Interaction with Composite Delamination［J］. Composite Structures， 2018， 206：484-498.

［5］  王兴国，吴文林，陈正林，等.LY12硬铝合金损伤缺陷的空气耦合超声检测［J］.中国机械工程，2017，28（21）：2582-2587.

WANG Xingguo， WU Wenlin， CHEN Zhenglin， et al. Air-coupling Ultrasonic Testing of Defects in LY12 Duralumin Alloys［J］. China Mechanical Engineering， 2017， 28（21）：2582-2587.

［6］  杨理践， 邹金津， 邢燕好. 电磁超声兰姆波在铝板传播中的模态识别［J］. 仪器仪表学报， 2014， 35（4）：909-916.

YANG Lijian，ZOU Jinjin，XING Yanhao. Modal Identification of Electromagnetic Ultrasonic Lamb Wave Propagation in Aluminum Plate［J］. Chinese Journal of Scientific Instrument. 2014， 35（4）：909-916.

［7］  江洋， 罗林， 王泽勇. 粘接结构的空气耦合超声导波检测仿真信号研究［J］. 通信技术， 2017， 50（6）：1188-1192.

JIANG Yang， LUO Lin， WANG Zeyong. Simulation Received Signal in Bonded-joint Inspection Using Air-coupled Guided Waves［J］. Communications Technology， 2017， 50（6）：1188-1192.

［8］  陈友兴. 多界面超声脱粘检测的方法研究及信号处理［D］.太原： 华北工学院， 2004.

CHEN Youxing. Method and Signal Processing for Ultrasonic Testing of Multi-layered Adhesive Interface［D］. Taiyuan：North China Institute of Techno-logy，2004.

［9］  徐鸿，郭鹏，李鸿源，等.基于SH模态导波杆的电站高温结构壁厚测量方法［J］.中国机械工程，2017，28（7）：757-763.

XU Hong， GUO Peng， LI Hongyuan， et al. Thickness Measuring Method of High-temperature Power Plant Structures Based on SH Mode Waveguide［J］.China Mechanical Engineering， 2017， 28（7）：757-763.

［10］  徐先纯， 郝娟， 郭灿志，等. 多层粘接材料深层界面脱粘的超声谐振检测方法［J］. 中国测试， 2022，48（2）：14-20.

XU Xianchun， HAO Juan，GUO Canzhi，et al. Ultrasonic Resonance Detection Method for Deep Interfacial Debonding of Multilayer Adhesive Materials［J］. China Measurement & Test， 2022，48（2）：14-20.

［11］  刘嘉同，金永，张浩亚，等. 基于多层界面脱粘的超声检测方法研究［J］. 国外电子测量技术， 2020， 39（9）：58-62.

LIU Jiatong，JIN Yong，ZHANG Haoya，et al. Multilayer Interface Debonding Study Based on Ultrasonic Detection Method［J］. Foreign Electronic Measurement Technology， 2020， 39（9）：58-62.

［12］  孙茂循， 项延训， 肖飚，等. 超声导波混频表征和定位早期局部损伤的研究进展［J］. 声学技术， 2022， 41（3）：313-322.

SUN Maoxun， XIANG Yanxun， XIAO Biao， et al. Early Detection of the Localized Damage Using Nonlinear Mixing of Guided Waves：a Review［J］. Technical Acoustics， 2022， 41（3）：313-322.

［13］  陳军， 李志浩， 林莉，等. 铝板中Lamb波检测的实验研究［J］. 应用声学， 2011， 30（2）：98-104.

CHEN Jun， LI Zhihao，LIN Li， et al. Experiment Investigations of Lamb Waves in an Aluminum Plate［J］. Journal of Applied Acoustics， 2011， 30（2）：98-104.

［14］  李德强. 基于超声导波的复杂板结构损伤识别研究［D］.大连：大连理工大学，2021.

LI Deqiang. Research on Damage Detection in Complex Plates Based on Ultrasonic Guided Wave［D］. Dalian：Dalian University of Technology， 2021.

［15］  ACHENBACH J D D. Wave Propagation in Elastic Solids［J］. Journal of Applied Mechanics， 1974， 16（2）：544.

［16］  马媛. 多界面粘接质量超声检测及信号处理技术［D］. 太原：中北大学.2021.

MA Yuan. Multi-interface Bonding Quality Ultrasonic Testing and Signal Processing Technology［D］.Taiyuan：North University of China，2021.

［17］  FAN Z， CASTAINGS M， LOWE M J S， et al. Feature-guided Waves for Monitoring Adhesive Shear Modulus in Bonded Stiffeners［J］. NDT & E International， 2013， 54：96-102.

［18］  MEI H， HAIDER M F， JAMES R， et al. Pure S0 and SH0 Detections of Various Damage Types in Aerospace Composites［J］. Composites Part B：Engineering， 2020， 189：107906.

［19］  KOODALIL D， BARNONCEL D， RAJAGOPAL P， et al. Detection of Interfacial Weakness in a Lap-shear Joint Using Shear Horizontal Guided Waves［J］. NDT & E International， 2020， 112：102248.

［20］  张超， 阎守国， 张碧星，等. 分层固体板中导波的激发与频散特性［J］. 声学学报， 2017， 42（1）：85-94.

ZHANG Chao， YAN Shouguo， ZHANG Bixing， et al. The Excitation and Dispersion Properties of Guided Waves in Multi-layered Plates［J］. Acta Acustica， 2017， 42（1）：85-94.

［21］  吕瑞宏， 杨佳怡， 张昊宇，等. 基于材料参数的管道防腐层粘接状态识别研究［J］. 仪器仪表学报， 2021， 42（5）：243-252.

LYU Ruihong， YANG Jiayi， ZHANG Haoyu， et al. Research on Identification of Adhesion State of Pipeline Coating Based on Material Parameters［J］. Chinese Journal of Scientific Instrument， 2021， 42（5）：243-252.

［22］  SONG H， POPOVICS J S. Characterization of Steel-concrete Interface Bonding Conditions Using Attenuation Characteristics of Guided Waves［J］. Cement and Concrete Composites， 2017， 83：111-124.

［23］  ROKHLIN S I. Lamb Wave Interaction with Lap-shear Adhesive Joints：Theory and Experiment［J］. Journal of the Acoustical Society of America， 1999， 89（6）：2758-2765.

［24］  王兴国， 刘红伟， 李晓高，等. 双层粘接界面特性的空气耦合超声导波检测［J］. 振动·测试与诊断， 2022， 42（1）：16-22.

WANG Xingguo， LIU Hongwei， LI Xiaogao， et al. Measurement Bonding Interface Characteristic of Two Layer Using Air Coupling Ultrasound Guided Wave［J］. Journal of Vibration， Measurement & Diagnosis， 2022， 42（1）：16-22.

［25］  杨理践， 赵丹铮， 高松巍. 基于超声兰姆波的管道防腐层缺陷检测方法［J］. 无损探伤， 2015（2）：6-9.

YANG Lijian，ZHAO Danzheng， GAO Songwei. Detection Method of Pipeline Anticorrosion Defects Based on Ultrasonic Lamwave［J］. Nondestructive Testing Technology， 2015（2）：6-9.

［26］  WANG X， WANG J，SHEN G， et al. Research on Interface Bonding Characteristics of Layered Medium Using Ultrasonic Oblique Incidence［J］. Composite Structures，2022， 295：115733.

［27］  J.L.罗斯.固体中的超声波［M］. 何存富， 吴斌，译. 北京：科学出版社，2004：82-88.

ROSE J L. Ultrasonic Waves in Solids［M］. HE Cunfu， WU Bin，Trans. Beijing：Science Press， 2004：82-88.

［28］  何存富，孙雅欣，吴斌，等. 高频纵向导波在钢杆中传播特性的研究［J］. 力学学报， 2007，39（4）：538-544.

HE Cunfu， SUN Yaxin， WU Bin， et al. Propagation Characteristics of High Frequency Longitudinal Guided Waves in Steel Rod［J］. Chinese Journal of Theoretical and Applied Mechanics， 2007， 39（4）：538-544.

（编辑  胡佳慧）

作者簡介：

吴  慧，男，1997年生，硕士研究生。研究方向为超声检测技术。E-mail：wwwwuhui97@163.com。

李晓高（通信作者），男，1980年生，讲师。研究方向为智能装备、无损检测。E-mail：lixiaogao@jcu.edu.cn。