致密储层敏感弹性参数叠前同步反演方法

桂金咏,高建虎,雍学善,李胜军,李海亮

(1.中国石油天然气股份有限公司勘探开发研究院西北分院,甘肃兰州730020;2.中国石油天然气集团公司油藏描述重点实验室,甘肃兰州730020)

致密储层敏感弹性参数叠前同步反演方法

桂金咏1,2,高建虎1,雍学善1,李胜军1,李海亮1

(1.中国石油天然气股份有限公司勘探开发研究院西北分院,甘肃兰州730020;2.中国石油天然气集团公司油藏描述重点实验室,甘肃兰州730020)

杨氏模量和泊松比是表征致密储层脆性的重要弹性参数,而Gassmann流体项则是地震流体识别中常用的流体因子。利用叠前地震反演方法从叠前地震资料中同步获取此类参数是可行且有效的途径。为此,针对致密储层预测及流体识别的需要,提出了一种致密储层敏感弹性参数叠前同步反演的新方法。在孔隙弹性介质反射系数近似方程的基础上,通过重新组合变化,推导出包含杨氏模量、泊松比、Gassmann流体项及密度参数的纵波反射系数方程,建立起了杨氏模量、泊松比、Gassmann流体项及密度反射率与纵波反射系数间的线性关系。在此基础上，采用基于贝叶斯理论的弹性阻抗反演技术,提出了杨氏模量、泊松比、Gassmann流体项及密度参数的叠前同步反演方法。模型数据试算和实际资料测试结果均表明,所提出的方法能够从叠前地震资料中稳定地获取致密储层的敏感弹性参数,为此类储层的预测及流体识别提供了一种可靠的技术途径。

致密储层；杨氏模量；泊松比；流体项；叠前同步反演

弹性参数(如纵、横波速度,拉梅参数,泊松比以及杨氏模量等)在地球物理勘探中具有极其重要的作用。不同岩石以及同一种岩石含不同流体时的弹性性质不同,反映在地震剖面上则是振幅响应不同。Zoeppritz方程的提出,建立起岩石弹性参数与地震振幅之间的联系,是叠前地震反演与流体识别的理论基础[1-2]。由于Zoeppritz方程高度非线性,求解极不稳定,Bortfeld[3]首次给出了Zoeppritz方程的近似方程,使得Zoeppritz方程中所暗含的振幅与岩石弹性性质间的关系更加明确。Aki等[4]给出了包含纵、横波速度和密度项的近似方程,是目前叠前地震反演中最为常见的Zoeppritz近似方程。Shuey[5]进一步研究了泊松比对反射系数的影响,首次提出了反射系数的AVO截距和梯度的概念,并证明了反射系数随入射角的变化梯度主要由泊松比的变化来决定,给出了用不同角度项表示的反射系数近似方程。Smith等[6]在Castagna泥岩基线的基础上,发现组合后的纵、横波速度反射率参数对流体极为敏感,首次提出“流体因子(fluid factor)”概念。Fatti等[7]重新组合了Aki-Richards近似方程,利用加权叠加的方法反演出了纵、横波阻抗反射率,并改进了Smith-Gidlow流体因子,使流体指示效果更稳定。Goodway等[8]提出了流体识别领域具有重大意义的LMR法,通过纵、横波阻抗转化计算得到拉梅参数和剪切模量与密度的乘积作为流体识别的指示工具。Gray[9]重新推导了Zoeppritz近似方程,提出了包含拉梅参数、剪切模量以及体积模量的纵波反射系数方程,无需纵、横波阻抗转化计算,可以直接同步反演出拉梅参数、剪切模量、密度等弹性参数。宗兆云等[10]利用叠前AVO反演方法得到了杨氏模量、泊松比参数作为储层预测参数。Russell等[11]基于孔隙弹性介质理论,提出了用于流体检测的Gassmann流体项的定义公式。后续学者研究认为Gassmann流体项作为新的流体因子较常规流体因子具有更高的流体敏感度[12-14]。

Connolly[15]提出了具有里程碑意义的弹性阻抗(Elastic Impedance,EI)反演理论。弹性阻抗反演结合了叠前AVO反演与叠后波阻抗反演的优点,基于抗噪性更好的叠前角度部分叠加道集、考虑了子波随炮检距的变化,利用传统叠后反演的方法即可得到对岩性以及流体更为敏感的弹性阻抗数据体[16-17]。在弹性阻抗数据体本身用于流体检测的同时,更多的是基于不同角度的弹性阻抗数据体同步反演出纵、横波速度以及密度等弹性参数。大量的理论研究与实际应用结果表明,这种方法能够提供更为可靠的弹性参数,能定量地反映储层信息,比传统叠前AVO反演方法得到的结果更精确、可靠且效率更高[13-20]。

随着油气勘探领域的不断扩大,全球油气勘探拓展到了非常规油气领域。致密油气,如致密砂岩油气、页岩油气等,作为全球重要的储备资源,其勘探开发技术成为目前研究的热点和难点。致密油气是指存在于致密储层中的非常规油气,具有强烈的低渗透特征,脆性较大,易压裂。地震岩石物理实验与勘探实践均表明,杨氏模量和泊松比能够较好地表征岩石的脆性,脆性较大的致密砂岩、页岩储层具有较高的杨氏模量和较低的泊松比特征[21]。本文推导出了一种新的纵波反射系数方程,利用该方程并采用弹性阻抗反演技术不仅可以有效地同步反演出杨氏模量、泊松比等致密储层预测中较为敏感的弹性参数,而且能同步反演出近年来流体检测领域备受关注的Gassmann流体项参数。以期在预测易脆储层的同时,检测出储层所含流体的类型。

1 反射系数方程

1.1 新的反射系数方程推导

Russell等[11]基于孔隙弹性介质理论,推导出了包含流体项(f)、剪切模量(μ)与密度(ρ)的AVO近似方程：

(1)

式中：θ为入射角度；γdry,γsat分别表示干岩石、饱和岩石纵横波速度比；Δf/f,Δμ/μ,Δρ/ρ分别表示流体项、剪切模量和密度的反射率。

流体项f与孔隙流体关系密切,与纵、横波速度及密度的关系为：

(2)

剪切模量μ与介质抗剪切性和刚度直接相关,与横波速度vS及密度ρ的关系为：

(3)

在各向同性介质中,杨氏模量E、泊松比σ与剪切模量μ的关系为：

(4)

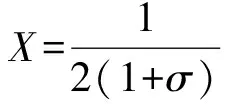
(5)

两边除以剪切模量可得：

(6)

又因：

(7)

式中：σ1,σ2分别表示上、下层介质的泊松比。

由于σ1=σ-Δσ/(2σ2)=σ+Δσ/2,则：

(8)

在各向同性介质中,泊松比σ与纵横波速度比γsat的关系为：

(9)

将(4)式至(9)式代入(1)式,得到：

(10)

方程(10)即为推导得到的新的反射系数近似方程,该方程成功地建立起了杨氏模量、泊松比以及流体项与反射系数间的关系。

1.2 近似精度分析

常规方法对于杨氏模量、泊松比及流体项的获取主要利用Aki-Richard近似方程建立反射系数与弹性参数间的关系,在反演得到纵、横波速度及密度之后,利用关系式转化为杨氏模量、泊松比及流体项等其它参数[18]。为了验证新的近似方程能否准确反映反射系数随偏移距变化的关系,利用Goodway等[8]提出的页岩与含气砂岩3层模型对新的反射系数方程近似精度进行分析,模型参数如表1所示。

表1 Goodway模型参数

模型饱和岩石纵横波速度比γsat=3.790,干燥岩石纵横波速度比γdry=2.333。利用(2)式、(4)式和(9)式将vP,vS,ρ转化为f,E,σ。利用精确Zoeppritz方程、Aki-Richard近似方程以及新推导的近似方程分别计算模型顶、底界面的反射系数,结果如图1和图2所示。从图1和图2可以看出,采用新近似方程与Aki-Richard近似方程计算的反射系数误差曲线,在入射角小于50°时几乎重合,差异极小。随着角度的增大,采用近似方程与精确Zoeppritz方程计算的反射系数误差逐渐增大。由图1b和图2b可以看到,大角度入射时,新近似方程计算的误差要小于Aki-Richard近似方程计算的误差。因此,利用新推导的反射系数方程计算的反射系数精度较高,能够适用于大角度入射情况下反射系数的求解,符合实际应用要求。另外,需要注意,同Russell近似方程一样,新的近似方程的近似精度也受γdry影响,实际应用时需要根据储层岩石的物理性质确定合适的干岩纵横波速度比γdry[11]。

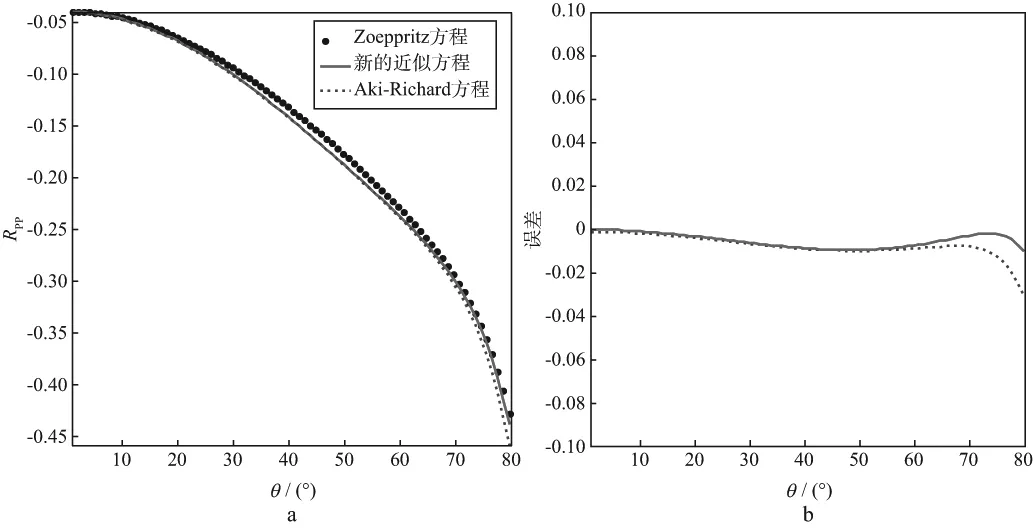
图1 顶界面反射系数(a)及其误差(b)随入射角的变化

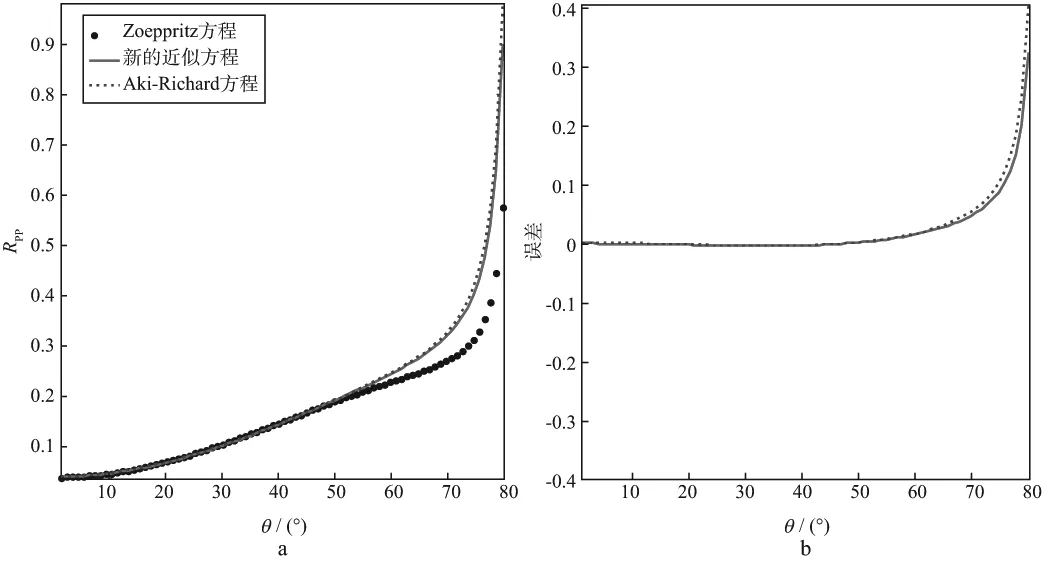
图2 底界面反射系数(a)及其误差(b)随入射角的变化

2 弹性参数反演

2.1 弹性阻抗方程

为了能稳定、高效地反演出与岩石脆性密切相关的杨氏模量、泊松比以及与流体密切相关的流体项,本文将新反射系数方程(10)进一步推导为弹性阻抗方程形式,基于弹性阻抗理论反演出此类参数。

依据Connolly[15]的弹性阻抗思想,反射系数与弹性阻抗的关系为：

(11)

代入到方程(10)有：

(12)

又Δx/x=Δlnx,则：

(13)

取积分并指数化,有：

(14)

其中,

(15)

同Connolly的弹性阻抗方程一样,方程(13)需要进行归一化处理,使不同角度弹性阻抗体量纲与声波阻抗一致[22],则有：

(16)

式中：I0为归一化因子；f0,E0,σ0,ρ0分别为目的层段流体项、杨氏模量、泊松比以及密度的平均值。其中,

(17)

方程(16)即为包含流体项、杨氏模量、泊松比以及密度的新弹性阻抗方程。

2.2 弹性阻抗反演

基于信噪比更高的角度部分叠加道集,利用弹性阻抗方程(16),采用传统叠后波阻抗反演方法即可得到新弹性阻抗数据体[18-20]。本文采用贝叶斯反演理论,通过求解最大后验概率密度来进行弹性阻抗反演。

与声波阻抗类似,给定角度θ,对反射系数r进行积分可以得到弹性阻抗：

(18)

式中：t是时间样点；t0是起始时间。

按照地震褶积模型：

d=Gr+n

(19)

式中：d=[d1,d2,…,dN]T是观测得到的地震数据；r=[r1,r2,…,rM]T是反射系数序列；G是N×M维子波矩阵；n=[n1,n2,…,nN]T表示观测噪声。

由贝叶斯公式可得以下近似式：

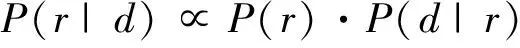
(20)

式中：P(r|d)表示反射系数的后验概率密度信息；P(r)表示反射系数先验概率密度信息；P(d|r)表示似然函数。

一般地面地震观测数据的噪声服从零均值、协方差矩阵为CS的高斯分布[23]。当给定反射系数r后,则观测数据与模型参数之间的似然函数P(d|r)可以通过该观测方式下噪声的分布特征来表示,即：

(21)

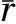
(22)

根据贝叶斯反演框架,后验概率分布表达了从观察数据中获得的对未知量的认知程度：

(23)

由贝叶斯理论可知,使(22)式取最大值的解为反射系数的最优解,即对模型参数的最大后验概率密度解。对(22)式两边同时取对数,整理后即可得到目标反演函数：

(24)

反演问题就变成了通过选择合适的r=[r1,r2,…,rM]T,使得目标函数为最小的过程。通过对(24)式求导,采用迭代重加权最小二乘算法即可对目标函数寻优,从而得到最佳的反射系数。将反射系数代入到(18)式,可得到最终的弹性阻抗数据。

2.3 敏感参数提取

弹性阻抗方程中有4个未知弹性参数,因此需要4个不同角度的弹性阻抗数据体参与提取。 对方程(16)两边取对数,得到：

(25)

给定角度θ,利用测井曲线拟合即可得到4个与角度有关的系数项a(θ),b(θ),c(θ),d(θ)。这样,对于4个不同角度的弹性阻抗数据I(θ1),I(θ2),I(θ3),I(θ4),可得到16个与角度有关的系数项。

在得到4个不同角度的弹性阻抗体和16个系数项后,根据方程(25),可以得到如下矩阵方程：

(26)

至此,将4个不同角度的弹性阻抗体和16个系数项代入方程(19)后,利用桂金咏等[25]提出的高稳健线性回归方法求解该线性矩阵方程,即可得到杨氏模量(E)、泊松比(σ)、流体项(f)和密度(ρ)。

3 反演效果测试

3.1 理论模型测试

利用实测测井数据(图3)作为模型测试数据。利用方程(16)以及模型数据合成角度分别为0,10°,20°,30°的4个弹性阻抗曲线(图4),通过添加不同程度噪声来测试方法的有效性。

图5为无噪声反演结果。从左到右,蓝色虚线为由测井曲线计算得到的流体项、杨氏模量、泊松比以及密度曲线,红色实线为本文方法反演曲线。由图5可以看出,在无噪声情况下,反演结果与原始模型曲线重合,说明方法在理论上完全可行。

对图4中弹性阻抗曲线添加随机噪声。图6为信噪比10∶1时的反演结果。图7为信噪比为5∶1时的反演结果。

图3 测井曲线

图4 不同角度的弹性阻抗曲线

图5 无噪声反演结果

由图6可以看到,在存在随机噪声的情况下,本文方法仍然能较高精度地反演出流体项、杨氏模量、泊松比和密度。比较图6和图7可以发现,随着噪声的增加,反演得到的流体项、杨氏模量、泊松比与密度的噪声也会增加,杨氏模量、泊松比、流体项、密度的反演精度会逐次降低。但是,即使在信噪比为5∶1的情况下,杨氏模量曲线同模型曲线的吻合度仍然较高,流体项曲线与泊松比曲线趋势与模型曲线也大致相同,精度在可接受范围内。与其它常规叠前地震反演方法一样,本文方法密度项的反演结果与模型差异较大,主要是因为在入射角较小(偏移距较小)的情况下,密度对反射系数的影响较小,易受噪声影响[26]。常规方法中,杨氏模量、泊松比、流体项的获取通常是利用叠前地震反演得到纵、横波速度以及密度项后,间接转化计算得到杨氏模量、泊松比及流体项。因此,在纵、横波速度和密度(尤其是密度)存在较大误差的情况下,常规方法转化计算得到的杨氏模量、泊松比及流体项势必会造成误差的累积。图8为信噪比10∶1时采用常规方法得到的反演结果。对比图6和图8 可以发现,同样是在信噪比为10∶1的情况下,常规方法反演结果较本文方法反演结果误差大,明显偏离真实值。其中,流体项与杨氏模量反演结果又较泊松比反演结果差,原因在于常规方法在对流体项、杨氏模量进行转化计算时有密度项参与,而密度项易受噪声影响,误差较大。

3.2 实际资料测试

实际资料来自某致密砂岩天然气藏研究区的一条二维测线。输入的4个不同角度的叠加道集地震剖面如图9所示,图中椭圆区域为储层发育区,可以发现,不同角度叠加道集振幅存在一定差异。利用本文方法进行二维剖面反演测试,得到的杨氏模量、泊松比、流体项剖面分别如图10,图11和图12所示。图中,投影曲线为相应的杨氏模量、泊松比、流体项测井曲线,虚线椭圆区域、实线椭圆区域试气结果分别为含水储层以及含气储层发育区。

图6 信噪比为10∶1的反演结果

图7 信噪比为5∶1的反演结果

图8 常规方法信噪比10∶1的反演结果

由图10至图12可以看到,剖面图中异常区域与杨氏模量、泊松比、流体项测井曲线异常区域均对应较好。其中,从图10中可以看到,杨氏模量高值异常区域与储层发育区域吻合较好,但含水与含气储层均呈高值异常,二者杨氏模量差异较小,不利于区分；图11中,泊松比低值异常区域与储层发育区域基本吻合,剖面上含气储层与含水储层泊松比值稍有差异,含气储层泊松比稍低于含水储层,但不明显；图12中,流体项虽不能完整地反映出上覆含水储层的分布,但能明显地指示出含气储层。因此,综合利用杨氏模量、泊松比以及流体项参数,可以准确地预测出储层发育区域,同时又能有效地识别出储层所含流体特征。

图9 不同角度叠加地震剖面

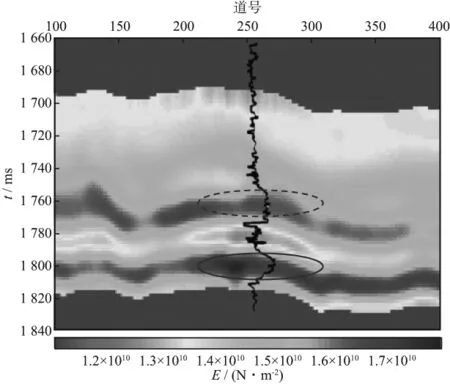
图10 杨氏模量反演剖面

图11 泊松比反演剖面

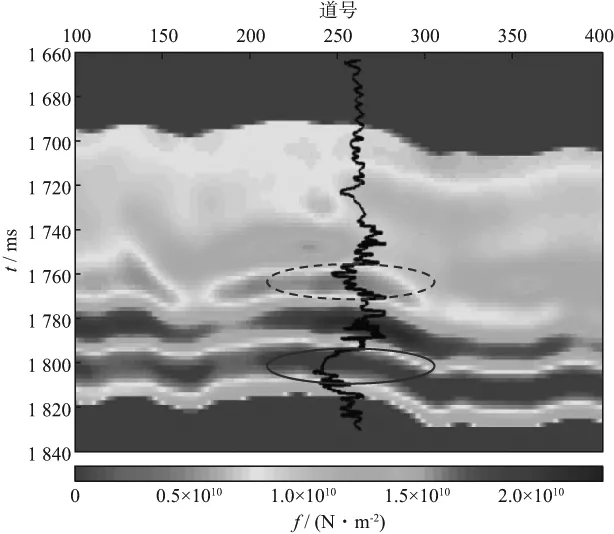
图12 流体项反演剖面

4 结束语

杨氏模量和泊松比能够较好地反映岩石的脆性,是致密储层预测的重要敏感参数,而Gassmann流体项对流体具有较高的敏感性,是储层流体检测中的重要流体因子。本文考虑到致密储层预测及流体识别的需要,基于Russell提出的Zoeppritz近似方程,推导得到了包含Gassmann流体项、杨氏模量、泊松比及密度的新Zoeppritz近似方程,建立起了叠前地震振幅与Gassmann流体项、杨氏模量、泊松比等致密储层敏感弹性参数间的直接联系。在新近似方程的基础上,采用基于贝叶斯理论的弹性阻抗反演方法,得到包含Gassmann流体项、杨氏模量及泊松比参数的弹性阻抗方程,利用4个不同角度的弹性阻抗数据直接反演出Gassmann流体项、杨氏模量、泊松比等致密储层敏感弹性参数,能有效克服常规方法依靠转化计算容易造成误差累积的缺点。模型数据试算及实际资料测试结果证明了该方法的有效性。

[1] Zoeppritz K.On the reflection and penetration of seismic waves through unstable layers[J].Goettinger Nachr,1919,1(7B):66-84

[2] Hilterman F J.Seismic amplitude interpretation:2001 distinguished instructor short course[M].Huston:Society of Exploration Geophysicists and European Associationof Gcostientists & Engineers,2001:3-4

[3] Bortfeld R.Approximation to the reflection and transmission coefficients of plane longitudinal and transverse waves[J].Geophysical Prospecting,1961,9(4):485-502

[4] Aki K,Richards P G.Quantitative seismology:theory and methods[M].USA:W H Freeman & Co Ltd,1980:123-192

[5] Shuey R T.A simplication of the Zoeppritz equations[J].Geophysics,1985,50(4)：609-614

[6] Smith G C,Gidlow P M.Weighted stacking for rock property estimation and detection of gas[J].Geophysical Prospecting,1987,35(9):993-1014

[7] Fatti J L,Smith G C,Vail P J,et al.Detection of gas in sandstone reservoirs using AVO analysis:a 3-D seismic case history using the Geostack technique[J].Geophysics,1994,59(9):1362-1376

[8] Goodway B,Chen T,Downton J.Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters[J].Expanded Abstracts of 67thAnnual Internat SEG Mtg,1997,183-186

[9] Gray D.Bridging the gap:using AVO to detect changes in fundamental elastic constants[J].Expanded Abstracts of 69thAnnual Internat SEG Mtg,1999,852-855

[10] 宗兆云,印兴耀,张峰,等.杨氏模量和泊松比反射系数近似方程及叠前地震反演[J].地球物理学报,2012,55(11):3786-3794 Zong Z Y,Yin X Y,Zhang F,et al.Reflection coefficient equation and pre-stack seismic inversion with Young’s modulus and Poisson’s ratio[J].Chinese Journal of Geophysics,2012,55(11):3786-3794

[11] Russell B H,Gray D,Hampson D P.Linearized AVO and poroelasticity[J].Geophysics,2011,76(3):C19-C29

[12] Feng H,Russell B H,Bancroft J C.A comparison of hydrocarbon indicators derived from AVO analysis[J].Consortium for Research in Elastic Wave Exploration Seismology Research Report,2007,19:1-9

[13] Zhang S,Yin X,Zhang F.Fluid discrimination study from fluid elastic impedance (FEI)[J].Expanded Abstracts of 79thAnnual Internat SEG Mtg,2009,2437-2441

[14] 印兴耀,张世鑫,张峰.针对深层流体识别的两项弹性阻抗反演与Russell 流体因子直接估算方法研究[J].地球物理学报,2013,56(7):2378-2390 Yin X Y,Zhang S X,Zhang F.Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification[J].Chinese Journal of Geophysics,2013,56(7):2378-2390

[15] Connolly P.Elastic impedance[J].The Leading Edge,1999,18(4):438-452

[16] Cambois G.AVO inversion and elastic impedance[J].Expanded Abstracts of 80thAnnual Internat

SEG Mtg,2000,142-145

[17] Mallick S.AVO and elastic impedance[J].The Leading Edge,2001,20(10):1094-1104

[18] 王保丽,印兴耀,张繁昌.弹性阻抗反演及应用研究[J].地球物理学进展,2005,20(1):89-92 Wang B L,Yin X Y,Zhang F C.Elastic impedance inversion and its application[J].Progress In Geophysics,2005,20(1):89-92

[19] Baoli W,Xingyao Y,Fanchang Z.Lamé parameters inversion based on elastic impedance and its application[J].Applied Geophysics,2006,3(3):174-178

[20] 桂金咏,印兴耀,曹丹平.基于弹性阻抗反演理论的泊松比反演方法研究[J].石油物探,2011,50(5):463-469 Gui J Y,Yin X Y,Cao D P.Poisson’s ratio inversion method based on elastic impedance inversion theory[J].Geophysical Prospecting for Petroleum,2011,50(5):463-469

[21] Sena A,Castillo G,Chesser K,et al.Seismic reservoir characterization in resource shale plays:stress analysis and sweet spot discrimination[J].The Leading Edge,2011,30(7):758-764

[22] Whitcombe D N.Elastic impedance normalization[J].Geophysics,2002,67(1):60-62

[23] Downton J.Seismic parameter estimation from AVO inversion[D].Calgary:University of Calgary,2005

[24] Youzwishen C F.Non-linear sparse and blocky constraint for seismic inverse problems[D].Alberta:University of Alberta,2001

[25] 桂金咏,印兴耀,高建虎,等.基于修正柯西分布的弹性参数反演方法[J].石油物探,2013,52(6):609-616 Gui J Y,Yin X Y,Gao J H,et al.The elastic parameters inversion based on modified Cauchy distribution[J].Geophysical Prospecting for Petroleum,2013,52(6):609-616

[26] Lines L R.Density contrast is difficult to determine from AVO[J].Canadian Journal of Exploration Geophysics,1998,47(1):1-8

(编辑：顾石庆)

A prestack simultaneous inversion method for sensitive elastic parameters of tight reservoir

Gui Jinyong1,2,Gao Jianhu1,Yong Xueshan1,Li Shengjun1,Li Hailiang1

(1.PetroChinaResearchInstituteofPetroleumExploration&Development-NorthWest,Lanzhou730020,China;2.ReservoirDescriptionKeyLaboratory,CNPC,Lanzhou730020,China)

Young’s modulus and Poisson’s ratio are the important elastic parameters representing the brittleness of tight reservoir rock,and Gassmann’s fluid item is regarded commonly as a fluid factor in seismic fluid identification.Prestack seismic inversion is a feasible and effective way to obtain such parameter from prestack seismic data.For the tight reservoir prediction and fluid identification,a new prestack simultaneous inversion method for sensitive elastic parameters of tight reservoir is proposed.Based on the pore elastic reflection coefficient approximate equation,we derive a P-wave reflection parameter equation of Young’s modulus,Poisson’s ratio,Gassmann’s fluid item and density.On this basis,a prestack simultaneous inversion method for sensitive elastic parameters of tight reservoir is constructed using the elastic impedance inversion technique based on Bayesian inversion framework.Model and actual data tests show that the newly proposed prestack simultaneous method can robustly obtain sensitive elastic parameters of tight reservoir from prestack seismic data,which offers a reliable technical approach for the tight reservoir prediction and fluid identification.

tight reservoir,Young’s modulus,Poisson’s ratio,fluid item,prestack simultaneous inversion

2014-11-20;改回日期：2015-02-10。

桂金咏(1986—),男,硕士,工程师,主要从事叠前地震反演及储层预测等方面的研究工作。

国家科技重大专项“大型油气田与煤层气开发”专题(2011ZX05007-006)资助。

P631

A

1000-1441(2015)05-0541-10

10.3969/j.issn.1000-1441.2015.05.007