二维TTI介质的纯P波波动方程数值模拟

张千祥,王德利,周进举

(吉林大学地球探测科学与技术学院，吉林长春 130026)

二维TTI介质的纯P波波动方程数值模拟

张千祥,王德利,周进举

(吉林大学地球探测科学与技术学院，吉林长春 130026)

声波各向异性数值模拟对地震数据处理和解释起着重要的作用。基于Tsvankin提出的精确色散关系,通过平方根近似,在时间-波数域中推导出二维TTI介质纯P波声波波动方程,并利用快速展开法(Rapid Expansion Method,REM)进行了数值模拟。与传统的有限差分法求解二维TTI介质耦合方程和傅里叶有限差分法在时间上进行波场外推相比,该方法的模拟结果精度更高,计算速度更快,并且成功去除横波分量。

声波各向异性数值模拟;纯P波声波方程;快速展开法;有限差分法;傅里叶有限差分法

地震数值模拟是地震勘探方法研究的前提和基础,在地震勘探和地震学的各项研究及生产工作中都扮演着重要的角色[1]。常用的地震波场数值模拟方法主要有几何射线法、波动方程法和积分方程法[2]。波动方程模拟方法中的有限差分法由于计算速度快、占用计算机内存小而被广泛应用。很早时候各国地球物理学家就对各向同性介质和各向异性介质弹性波地震数值模拟进行了深入研究。近年来,周进举等[3]利用高阶旋转网格有限差分法研究了复杂介质下弹性波数值模拟。

在对地下的各向异性介质进行弹性波数值模拟时,由于弹性波方程复杂,各向异性参数多,导致模拟计算量大,耗时长,增加了弹性波偏移和干涉的难度。为了解决这些问题,我们采用声波各向同性近似理论,通过设定弹性波中的横波速度为零来简化计算参量,在保证模拟精度的条件下提高计算效率。然而,由于地下介质的不均匀性,这种各向同性的声学假设常常是不恰当的。因此,在各向异性介质的情况下,需要提出一个合理的正演模拟方法来提高声波各向异性数值模拟的精度,并显著缩短计算时间。

多年来,人们对于各向异性介质发展了多种P波正演算子[4-5],但是这些正演算子大多针对具有垂直对称轴的各向同性介质(Transversely isotropic media with a vertical symmetry axis,VTI介质)的。VTI介质在沉积盆地中广泛存在[6],然而,这种假设只对一些简单的地质形态有效,例如介质中的岩层面平行于记录面。当地下的岩层面倾斜时,各向同性介质(Transversely isotropic media,TI介质)的对称轴可能不垂直,这种介质通常被称为有倾斜对称轴的各向同性介质(Transversely isotropic media with a tilt symmetry axis,TTI介质),通常在有背斜构造或者逆冲推覆体的区域广泛发育。自从Alkhalifah等[7]在VTI介质研究中引入了“声学”近似,许多地球物理学家在VTI介质的建模和正演中进行了更深入研究,并逐渐向TTI介质扩展,发展了许多形式不同的二维TTI介质声波各异性波动方程和各种高精度、低频散的数值模拟方法。2001年Klie等[8],2006年Zhou等[9],2007年Hestholm[10]都基于Alkhalifah声学假设对VTI介质进行了声波数值模拟。之后,2009年Fletcher等[11]通过旋转对称轴导出了TTI介质声波波动方程。近年来,Barrera等[12]提出了不含有横波的纯P波波动方程并成功的应用到逆时偏移中。Kim等[13]在前人研究的基础上对纯P波波动方程在数值模拟实现上进行了改进,采用图形处理器(Graphic processing unit,GPU)提高了计算速度。

我们从Tsvankin[14]提出的精确色散关系出发,得到近似P波色散关系,并构建一个二维TTI介质的纯P波模式的拟微分声波方程,然后应用快速展开法进行数值实现。与传统的有限差分法(Finite difference method,FDM)[15]和傅里叶有限差分法(Fourier finite differences,FFD)[16]相比,该方法不仅能很好去除频散，提高计算效率,还能去除SV波分量。

1 方法原理

1.1 二维TTI介质耦合方程

首先从Tsvankin[17]提出的精确相速度表达式开始推导:

(1)

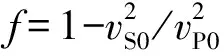
(2)

其中微分算子H1和H2被定义为：

(3)

对耦合方程(2)中的时间导数和空间导数分别用有限差分法进行求解,但这种方法会随着有限差分项的阶数变高而变得繁琐。因此,我们结合傅里叶变换和有限差分法来简化方程的推导和求解。

1.2 傅里叶有限差分法

我们提出了一个波场延拓的新方法,该方法结合了傅里叶变换和有限差分法。具体推导过程见附录A。对于复杂速度模型的正演模拟,该方法具有较高的精确性和稳定性;对于二维TTI介质的数值模拟,该方法能很好的去除横波分量,但容易出现频散效应,模拟效果不是最佳。我们从Tsvankin提出的精确相速度开始推导,得出纯P波声波方程,并用快速展开法进行求解,取得了很好的效果。

1.3 二维TTI介质的纯P波波动方程

(4)

方程(4)对于P波色散关系式是一个很好的近似[19-20],当满足：

(5)

(6)

其中F=1+2ε/f,令ε=0,方程(6)简化为：

(7)

方程(7)对于VTI介质也是成立的。对于对称轴有任意取向的TTI介质,可以由方程(7)通过一个描述绕Z轴逆时针旋转的变量推导出来。在旋转的坐标系下,波速算子为：

(8)

其中，θ和φ是互余的关系,从方程(8)我们可以得出：

(9)

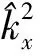
(10)

把方程(10)的两边在傅里叶域中同时乘以波场函数p(ω,kx,kz),然后,对方程两边同时用傅里叶逆变换,之后由关系式iω↔∂/∂t,最终得出二维TTI介质在时间-波数域中纯P波波动方程：

(11)

1.4 快速展开法

定义伪-差分算子L为：

(12)

方程(11)可以表示为：

(13)

(14)

进而得出p-t项为：

(15)

将方程(14)和方程(15)相加,应用快速展开法进行数值求解,求解方程为：

p(t+Δt)=-p(t-Δt)+2cos(LΔt)p(t)

(16)

在方程(16)中余弦函数的正交多项式展开式可表示为[21]：

(17)

其中,当k=0时,C2k=1;当k>0时,C2k=2。R是L2的最大特征值。J2k为第一类贝塞尔函数,Q2k为切比雪夫多项式,满足如下的循环关系：

(18)

式中：I是单位矩阵。

当M>RΔt时,方程(17)以指数形式收敛。因此,当M的取值略微大于RΔt时,方程的总求和项可以被大大的缩短。Pestana等[19]已经证实,当M=1时,也就是说求和中只有两项,这种使用切比雪夫多项式的余弦函数的近似相当于在时间上的二阶有限差分格式。当M=2时,包含了L4算子项,这种近似等价于Dablain[22]提出的时间上的四阶有限差分格式。

2 数值计算实例

为了验证本文提出的纯P波声波方程的有效性,我们设计了一个模型并对其进行数值模拟。模型大小为4000m×4000m,震源是雷克子波,主频30Hz,网格间距为Δx=Δz=10m,时间采样间隔为0.1ms,vP0=3000m/s,ε=0.24,δ=0.1。

图1a到图1d分别代表θ为0,30°,60°,90°时所对应的波场快照。从图1可以看出数值模拟效果很好,成功去除了横波,证明了本文方程的有效性。

接下来通过与传统有限差分法求解声波耦合方程和傅里叶有限差分法波场数值模拟的比较来证明快速展开法的优势。模拟时,震源子波采用主频30Hz的雷克子波,传播速度vP0=3000m/s,Thomsen参数ε=0.20,δ=0.05,模型大小同样为4000m×4000m。

图2a对应有限差分法求解TTI耦合方程(2)得到的波场快照，空间网格间距10m×10m;图2b 对应傅里叶有限差分法进行时间上的波场外推得到的波场快照，空间网格间距5m×5m;图2c 为应用快速展开法在时间—波数域中求解二维TTI介质纯P波声波方程(11)得到的波场快照，空间网格间距10m×10m。

图1 二维TTI介质在传播时间为0.5s的波场快照

图2 不同方法求解出的二维TTI介质在传播时间为0.6s的波场快照

有限差分法求解TTI耦合方程时，时间上采用二阶、空间上采用六阶有限差分形式，计算时间为273s，而应用快速展开法的计算时间只需要147s。对比图2a和图2c可以看出，应用快速展开法不但很好地去除了横波分量，还大大缩短了计算时间。对比图2b与图2c发现,虽然傅里叶有限差分波场外推也能很好地去除横波分量,但计算时采用的网格间距小,图2b上频散效应还很严重。当两种方法参数相同时,傅里叶有限差分法计算时间为156s。两种方法都是在频率域计算,模拟时间相差不多。综上所述,本文采用的快速展开方法进行数值模拟具有很强的优越性。

利用本文方法对三层均匀介质模型进行正演模拟。速度模型如图3所示。

震源子波采用主频为40Hz的雷克子波,时间步长0.2ms,网格间距给定为15m×15m,传播时间为0.5s时的波场快照如图4所示。

图5a和图5b分别给出了合成的BP速度模型以及应用快速展开法进行数值模拟的结果。模拟时采用峰值频率为50Hz的雷克子波,水平网格间距为20m,垂直网格间距为10m,时间采样间隔为0.5ms,传播时间为1.5s。

图3 三层均匀介质速度模型

图4 采用本文方法对三层均匀介质模型正演模拟波场快照

由图4可看出，在地下2.0km和3.1km处存在明显的反射和透射，并且没有横波波前面，与图3所示的速度模型相吻合。在图5b中也显示出了地下介质中高速体的存在。由此可知，本文所提出的方法可以很好地应用于复杂模型的正演模拟。

图5 BP速度模型(a)和本文提出的快速展开法数值模拟结果(b)

3 结论

1) 利用传统的有限差分法进行数值模拟时,我们只是假定了沿对称轴的剪切波速度为零,而不是在任意方向剪切波的速度都为零。所以快照图中还会产生横波分量,且出现一定的频散效应,加大有限差分的阶数减小频散时,又会大大地增加计算量和计算时间。

2) 通过傅里叶有限差分法对地震波场在时间上进行外推时,虽然横波分量被很好地去除掉,但在网格间距很小的情况下频散效应还是很严重,效果不理想,不适合应用到实际情况下的数值模拟。

3) 通过快速展开法在时间-波数域对二维TTI介质纯P波声波方程进行数值模拟时,有效去除了横波分量,缩短了计算时间,提高了计算效率；网格间距很大时也能取得良好的模拟效果,没有频散效应。所以当模拟区域比较大的时候,在保证相同的模拟效果情况下能大大地缩短模拟时间。

4) 本文的研究成果也能很好地应用于复杂介质的正演模拟,为以后TTI介质的逆时偏移(RTM)、声波干涉和全波形反演(FWI)等提供了可靠的技术手段。

[1] 陈洪杰.基于声波方程的数值模拟与逆时偏移方法研究[D].吉林大学,2010 Chen H J.Numerical simulation and reverse-time migration method research base on acoustic wave equation[D].Jilin University,2010

[2] 张永刚.地震波场数值模拟方法[J].石油物探,2003,42(2)：143-148 Zhang Y G.On numerical simulations of seismic wavefield[J].Geophysical Prospecting for Petroleum,2003,42(2):143-148

[3] 周进举,王德利.含倾斜裂隙页岩介质地震波场传播特征研究[J].石油物探,2014,53(5):501-508 Zhou J J,Wang D L.Research of wave field propagation characteristics of shale medium containing tilt fracture[J].Geophysical Prospecting for Petroleum,2014,53(5):501-508

[4] Han Q,Wu R S.A one-way dual-domain propagator for scalar qP-waves in VTI media[J].Geophysics,2005,70(2):D9-D17

[5] Zhang L,Hua B,Calandra H.3D Fourier finite-difference anisotropic depth migration[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005,1914-1917

[6] Crampin S,Chesnokov E M,Hipkin R A.Seismic anisotropy—the state of the art[J].First Break,1984,20(3):9-18

[7] Alkhalifah T.An acoustic wave equation for anisotropic media[J].Geophysics,2000,65(11):1239-1250

[8] Klie H,Toro W.A new acoustic wave equation for modeling in anisotropic media[J].Expanded Abstracts of 71stAnnual Internat SEG Mtg,2001,1171-1174

[9] Zhou H,Zhang G,Bloor R.An anisotropic acoustic wave equation for VTI media[J].Expanded Abstracts of 68thEAGE Annual Conference,2006,H033

[10] Hestholm S.Acoustic VTI modeling using high-order finite-differences[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007,139-143

[11] Fletcher R P,Du X,Fowler P J.Reverse-time migration in tilted transversely isotropic(TTI) media[J].Geophysics,2009,74( 6):WCA179-WCA187

[12] Barrera D F,Pestana R C.Pseudo-acoustic wave equation for modeling and reverse time migration in TTI media[J].Journal of Seismic Exploration.2013,22(1):33-48

[13] Kim Y S.Acceleration of stable TTI P-wave reverse-time migration with GPUs[J].Computers & Geosciences,2013,52(1):204-217

[14] Tsvankin I.Seismic signatures and analysis of reflection data in anisotropic media[M].Tulsa:SEG,2012,1-433

[15] Zhou H B,Zhang G Q,Bloor R.An anisotropic acoustic wave equation for modeling and migration in 2D TTI media[J].Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006,194-198

[16] Song X L,Fomel S.Fourier finite-difference wave propagation[J].Expanded Abstracts of 80thAnnual Internat SEG Mtg,2010,3204-3209

[17] Tsvankin I.P-wave signatures and notation for transversely isotropic media:an overview[J].Geophysics,1996,61(2):467-483

[18] Thomsen L.Weak elastic anisotropy[J]:Geophysics,1986,51(11):1954-1966

[19] Pestana R C,Stoffa P L.Time evolution of the wave equation using rapid expansion method[J].Geophysics,2010,75( 4):T121-T131

[20] Pestana R C,Ursin B,Stoffa P L.Separate P- and SV-wave equations for VTI media[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011,163-167

[21] Tal-Ezer H,Kosloff D,Koren Z.An accurate scheme for seismic forward modeling[J].Geophysical Prospecting,1987,35( 5):479-490

[22] Dablain M A.The application of high-order differencing to the scalar wave equation[J].Geophysics,1986,51(1):54-66

附录A

对各向同性介质有：

(A1)

其中p(x,t)是地震压力场,v(x)是传播速度。假定一个常速度v,经过空间中的傅里叶变换,我们得到如下的表达式：

(A2)

其中

(A3)

方程(A2)有如下的解：

(A4)

对时间应用二阶有限差分和逆傅里叶变换，得到：

(A5)

(A6)

v1是对称面上的P波相速度,v2是垂直于对称面方向上的P波相速度,η是各向异性弹性参数,它与Thomsen弹性参数ε和δ有关：

(A7)

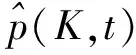
4) 将通过泰勒展开得到的系数应用到q(x,)来得到q(x,t+Δt);

5)q(x,t+Δt)+2p(x,t)-p(x,t-Δt)→p(x,t+Δt)。

(编辑：朱文杰)

Acoustic wave equation numerical simulation for pure P-wave in 2D TTI medium

Zhang Qianxiang,Wang Deli,Zhou Jinju

(JilinUniversity,Changchun130026,China)

Anisotropic numerical simulation of acoustic wave plays an important role in seismic data processing and interpretation.Starting with the exact dispersion relationship derived by Tsvankin and a square root approximation，we proposed a pure P-wave acoustic equation for 2D TTI medium in time-wavenumber domain,then the rapid expansion method (REM) is applied for numerical simulation.Compared with the conventional finite difference method to solve the 2D TTI medium coupled equations and Fourier finite difference to implement wavefield extrapolation in time,the synthetic data test results of our method is advanced in high precision and fast computing speed; what’s more,the SV-wave component has been removed successfully.

anisotropic numerical simulation of acoustic wave,pure P-wave acoustic equation,rapid expansion method,finite difference method,Fourier finite difference method

2015-01-14;改回日期：2015-03-30。

张千祥(1992—),男,硕士,现从事声波各向异性正演数值模拟研究工作。

王德利(1973—),男,教授,博士生导师,主要从事各向异性介质波场正、反演理论和高精度地震勘探研究工作。

国家自然科学基金项目(41374108)和国家科技重大专项(2011ZX05023-005-008)联合资助。

P631

A

1000-1441(2015)05-0485-08

10.3969/j.issn.1000-1441.2015.05.001