基于时频分析的初至拾取方法研究
2015-06-27刘怀山徐秀刚
岳 龙,刘怀山,刘 凯,徐秀刚,邢 磊
(中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛266100)
基于时频分析的初至拾取方法研究
岳 龙,刘怀山,刘 凯,徐秀刚,邢 磊
(中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛266100)
地震记录的初至拾取是地震资料处理的基础工作,特别是静校正、层析成像等后续处理对初至拾取的精度要求较高。当初至波到达时,其信号的振幅、频率、相位均会发生变化,基于此,提出了一种基于时频分析的初至拾取算法,该算法在噪声判别系数的约束下,利用小波变换时频分析提取信号的瞬时相位谱,然后利用瞬时相位谱的过零点属性拾取初至。为了提高计算效率,在给定时窗内部计算信号的瞬时相位谱,并且利用多个不同的噪声判别系数初至拾取的统计结果确定最终的初至时间。理论信号和实际地震资料处理结果表明,该方法具有较好的抗噪能力,初至拾取的精度比较高。
初至拾取;小波变换;时频分析;瞬时相位谱;噪声判别系数
初至波拾取在地震资料处理中应用广泛,特别对于地表静校正[1]、井间地震勘探和层析成像[2]有着重要作用。目前已经有很多初至拾取的算法,包括Gelchinsky提出的相关法[3]、Coppens提出的能量比法[4]等。相关法受续至波的影响比较大,能量比法受到时窗大小的限制[5]。此外,还有一些方法如分形分维法[6]、人工神经网络[7]和基于图像处理的方法[8]等也被应用于地震资料的初至拾取。
综合研究上述初至拾取算法,发现当初至波附近信噪比较高时,这些方法都能够准确拾取初至,但当初至波附近信噪比较低或者在强能量直达波之前存在小能量折射波的情况时,相关法、能量比法等方法无法准确拾取初至。
基于此,我们提出了利用时频分析进行初至拾取。当初至波到达的时候,地震信号的能量、频率和相位都会发生变化,同时地震信号初至附近存在噪声干扰,此时,可以利用有效信号和干扰在时频域的差异进行初至信号识别。
传统的时频分析方法包括短时傅里叶变换、小波变换、S变换和Wigner分布、Cohen类时频分布。本文选用小波变换作为时频分析工具,利用小波变换得到信号的瞬时相位谱,信号瞬时相位谱的第一个正向过零点(即瞬时相位由负到正变化)的位置,即为初至波向下起跳的波谷位置。为了提高初至拾取的精度,在计算完成后,对初至拾取的奇异点进行检测,得到最终的初至时间。值得注意的是:本文拾取的初至时间是初至波向下起跳的波谷位置,而不是起跳点,因为波谷位置能量强,更易于识别。
1 连续小波变换
小波变换是在短时傅里叶变换的基础上发展起来的,相对于短时傅里叶变换,小波变换具有多分辨率的特性,这一特性可以通过母小波的伸缩和平移来实现。母小波函数ψ(t)的定义:
(1)
把满足条件(1)式的小波称为允许小波或者母小波,其中Ψ(ω)是ψ(t)的频谱。
则:

(2)
可见,小波函数ψa,b(t)是由母小波函数通过伸缩和平移而得到。其中a为尺度参数,b为平移参数。
连续小波变换的定义为:
(3)

短时傅里叶变换的窗函数固定,因此其时间和频率分辨率不能兼顾。小波变换是短时傅里叶变换的发展,具有多分辨率的特性,在高频处,分析时窗变窄,在低频处,分析时窗变宽,能够很好的适用于非平稳信号的分析。
2 小波变换时频分析初至提取
2.1 小波变换瞬时相位计算
利用小波变换得到地震信号的时频谱,然后利用谱峰检测[9]方法计算地震信号的瞬时相位谱。在计算地震信号瞬时相位谱的过程中,需要给定一个噪声判别系数a0,当某一时刻时频谱能量的最大值小于分析信号的时频谱的平均值的a0倍时,判定该时刻的信号是随机噪声,规定其瞬时相位为0。反之,如果大于分析信号的时频谱的平均值的a0倍时,计算该时刻最大时频谱对应的瞬时相位,噪声判别条件和瞬时相位计算公式为:
(4)
(5)
其中,|Wf(a,bmax)|是a时刻最大的时频谱能量,对应的尺度是bmax。mean[|Wf(a,b)|]表示信号二维时频谱绝对值的平均值。I(a)是a时刻的瞬时相位,Imag[Wf(a,bmax)]是时刻a,尺度bmax对应的时频谱的虚部,Real[Wf(a,bmax)]是时刻a,尺度bmax对应的时频谱的实部。
如果地震资料信噪比较低,可以通过比较大的噪声判别系数序列来进行初至拾取。但要慎用去噪处理,去噪可能会改变信号的振幅和相位,造成初至位置和原始初至位置有所差异。
2.2 利用小波变换时频分析实现初至波自动拾取
利用小波变换时频分析方法实现初至波的自动拾取包括以下步骤:
1) 首先将地震道反转,然后计算其希尔伯特变换,得到地震道的解析信号道,对解析信号道进行时频分析。
2) 计算近偏移距道的时频谱,寻找瞬时相位谱第一个正向过零点的位置,即为该道的初至时间t0。在拾取该道的瞬时相位谱的过程中使用比较大噪声判别系数(一般0.2就可以满足要求),近道直达波能量比较强,选择大的噪声判别系数可以尽可能逼近第一道地震记录的初至。
3) 为了不过分依赖第一道初至拾取的结果,防止其拾取误差较大,对后续道初至拾取产生影响,在拾取下一道初至时间时,对其采用不加时窗全道参与计算和加时窗部分参与计算两种方式,拾取两个初至时间,如果这两个初至时间相同,则说明第一道拾取的初至时间接近真实位置,如果两个计算结果不同,说明第一道初至拾取有问题,则以第二道全道参与计算得到的初至时间为准,继续相同的步骤,直到两种方式计算的初至时间相同;之后后续道的计算直接采用划定时窗的方式,在时窗内部计算初至时间。在上述基础上,得到了近偏移距道的初至时间t0,则下一道的初至时间应该在t0附近的一个时窗内,因此在计算下一道的时频谱之前,以t0为中心,划定一个时窗,在该时窗内部计算时频谱。时窗的宽度,以t0为中心,向前扩充N个样点,向后扩充M个样点,记为N~M。
4) 在第3)步基础上,采用给定的噪声判别系数计算瞬时相位谱,在本道地震记录瞬时相位谱上,自动拾取t0(上一道初至时间)前后最近的两个正向过零点(为了应对初至时间变化比较大的情况,每道地震记录t0前后均要自动拾取一个正向过零点),在这两个过零点中,选取距离t0最近的作为这一道的初至时间。如果初至随偏移距逐渐变大,在t0前没有正向过零点,则该道的初至时间就是t0后第一个正向过零点位置的时间。
5) 给定一系列噪声判别系数,从0开始,以0.01为间隔直到0.1,重复第4)步,得到11个初至时间曲线,然后选择远偏移距位置共炮点地震道数的1/5,计算相邻两个噪声判别系数对应的初至时间差值的绝对值之和,然后平均到每道,当连续m个噪声判别系数计算的差值接近或等于0且m/11最大的时候,该初至时间即为准确的初至时间。
6) 重复步骤3)到步骤5),直到完成所有地震道的初至拾取。如果计算的相邻两道初至波时差大于两个子波视周期,那么需要对其准确性进行检测,根据相邻道波形相似的原则,在第3)步给定的时窗内,对两道作互相关,计算相邻道的时差,如果相关时差和本方法拾取的时差差别在1/4个子波视周期以内,则认为拾取的初至正确,继续后续道的计算,如果两个时差差别较大,则以相关时差为准修正本方法拾取的初至,继续后续道的计算。
7) 利用相位域初至起跳[5]技术,计算相邻过零点位置的间隔ΔT,将反极性初至波波谷位置向前移动ΔT/2的采样点,即为初至波波谷的位置,如果为了得到初至波起跳位置,可以向前移动大约3ΔT/4。
为了提高算法的稳定性,需要规定初至拾取的几个参数。
1) 给定的时窗宽度T的大小,可以比较随意一些,但是不能够太小,至少要满足初至波包含在里面且在时窗内部有不小于3个子波视周期,N不小于子波视周期的一半,M不小于2.5倍的子波视周期;
2) 上述初至波自动拾取的第4)步理论基础是,在野外采集过程中,为了防止出现空间假频,道间距应该满足一定的条件[10-11],相邻道的初至波时差Δt小于半个子波视周期T*:
(6)
2.3 理论信号的初至拾取实验
为了验证时频分析初至拾取的可行性,设计一个正弦信号和阻尼拉伸正弦子波(李子波)[12],并利用连续小波变换分析理论信号的瞬时相位谱。连续小波变换采用的时频分析参数为分析小波为复高斯小波,即高斯函数的2阶导数;尺度变量为fscal:
(7)
其中,fw是母小波的主频,Scal是尺度的个数,一般为2N。a=Scal,Scal-1,…,1,文中Scal为256。
正弦信号频率10Hz,初始相位-π,采样率为1ms,如图1所示。从图1中可以看出,正弦信号的瞬时相位谱过零点位置和正弦波波谷在同一个位置。二者的对应情况如表1。
为了检测小波变换时频分析的抗干扰能力,在图1所示正弦波的基础上加上一定的随机噪声(图2),对含噪正弦波进行时频分析,得到其瞬时相位谱,并拾取其瞬时相位谱过零点位置,统计结果如表2。
从表2可以看出,随着信噪比的降低,瞬时相位谱过零点位置偏离正弦信号波谷位置越来越大,但是每个瞬时相位谱过零点位置都在波谷附近几个样点之内。对正弦信号的分析证明,通过瞬时相位谱的过零点来拾取正弦波波谷位置是可行的。
分析表3可得,噪声判别系数在0~0.1变化,对理论信号而言,相邻噪声判别系数波谷时间差在2~3个样点之内,所以可以作为实际信号噪声判别系数范围的参考。
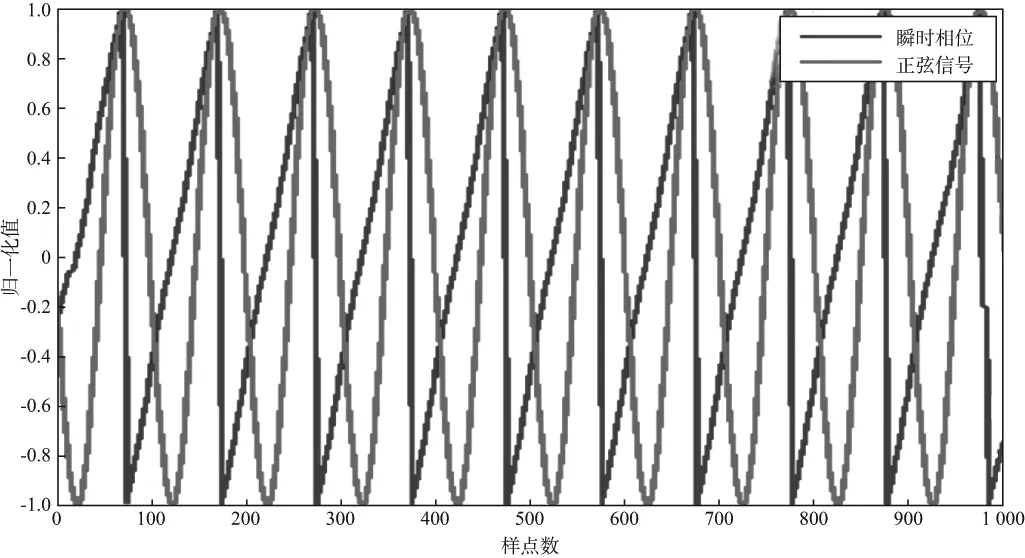
图1 正弦信号及其瞬时相位谱(归一化)
表1 正弦波波谷及其相位过零点位置

正弦波波谷位置(样点数)25125225325425525625725825925瞬时相位谱过零点位置(样点数)25125225325425525625725825925

表2 不同信噪比信号相位过零点位置

表3 不同噪声判别系数波谷时间差(信噪比为1)
野外实际地震资料的地震子波都是混合相位子波,子波的第一个下跳的波谷很小,随后的波峰及波谷很大[13],而最适于表达实际爆炸地震子波就是李子波[12],李子波是李庆忠院士提出的一种子波模型。鉴于此,利用小波变换对李子波进行分析。李子波的表达式:
(8)
式中:a,b,c,rat为给定的常数;sin[2πf0t/(1+rat)]为拉伸正弦函数;taexp(-btc)为阻尼包络;Amax为该阻尼包络的极大值。
(9)
李子波波形不符合初至波起跳向下的规定[13],所以将李子波极性反转,计算其瞬时相位谱(图3)。李子波极性反转后,波谷和瞬时相位谱过零点位置的对应关系如表4。
由表4可以看出,前2个强能量波谷和过零点位置的误差比较小,第3个波谷的误差比较大,主要原因是第3个波谷位置能量比较小,受相邻波形的影响,拾取精度有所降低。

表4 反极性李子波相位过零点位置
对李子波添加一定的随机噪声(图4),然后拾取其瞬时相位谱的过零点位置,为了降低随机噪声产生程序对拾取结果的影响,相同信噪比下生成多个不同的噪声信号,对含噪李子波拾取瞬时相位谱统计过零点位置。统计结果如表5。
从表5可以看出,在信噪比为2的情况下,反极性李子波前两个波谷位置和瞬时相位谱过零点位置基本上吻合,第三个波谷因为能量小,受随机噪声的影响比较大,拾取的瞬时相位谱过零点位置误差偏大。

图2 含不同噪声能量的正弦信号
通过对正弦信号、李子波的实验,时频分析方法能够很好的拾取理论信号起跳点的波谷位置,因此可以将其应用到实际资料当中。

图3 反极性李子波及其瞬时相位谱

图4 加噪反极性李子波
表5 加噪反极性李子波相位过零点位置
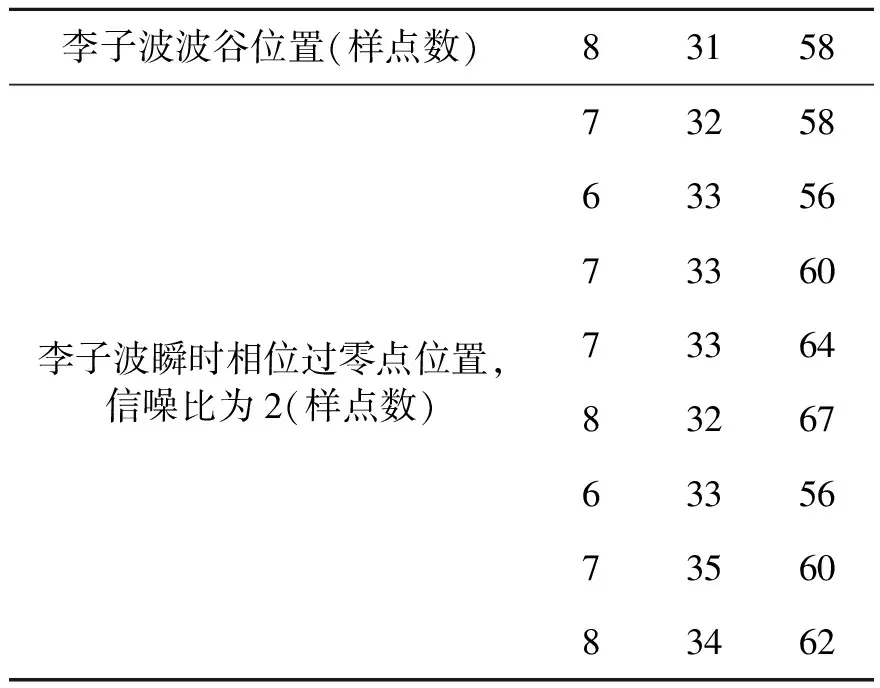
李子波波谷位置(样点数)83158李子波瞬时相位过零点位置,信噪比为2(样点数)7325863356733607336483267633567356083462
3 应用效果分析
为了检验本方法的实际应用效果,首先对某油
田陆上二维测线的地震数据拾取初至,野外采集参数为中间放炮,记录道数180道,最小偏移距为150m,最大偏移距4600m,道间距为50m,采样间隔为2ms,记录长度6s。该工区地表比较平坦,在远偏移距处折射波比较发育,但相对于直达波能量较弱。
3.1 单道地震记录分析
选取二维地震资料中的一道地震数据(图5),对其进行分析,结果见图6。
从表6可以看出,第1个和第5个波谷位置和过零点位置误差比较大,原因是在这两个位置能量比较小,在小波分析过程中受到相邻波形的影响比较大,而另外几个波谷位置拾取准确。

表6 初至波波谷及瞬时相位过零点位置

图5 单道地震记录(归一化)
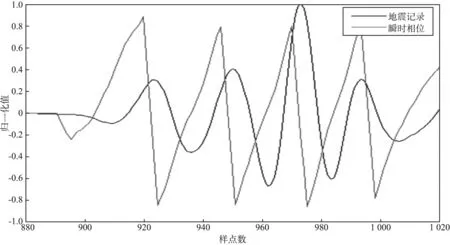
图6 初至波及其瞬时相位谱(归一化)
对图5中地震记录加上随机噪声,再计算其瞬时相位谱,结果如图7所示。
图中方框标注位置是初至波波谷位置,可以看出,受到噪声的影响,视觉上已经很难判断波谷的具体位置。
由表7可以看出,利用瞬时相位拾取的初至波第1个波谷位置误差比较大。因此,如果地震资料初至波附近信噪比较低,导致初至波起跳波谷被噪声淹没,可以先将地震波极性反转,将强能量的波峰转变为波谷,拾取后续波峰位置。应用效果如图8,统计结果见表8。

图7 含噪初至波及其瞬时相位谱
表7 含噪初至波波谷及相位过零点位置

初至波波谷位置(样点数)9099369629831006过零点位置(样点数)9009369629841010

图8 极性反转初至波及其瞬时相位谱
表8 反极性初至波波谷位置及相位过零点位置

反极性初至波波谷位置(样点数)924950973993过零点位置(样点数)923949973995
从表8可以看出,初至波波峰能量较强,局部信噪比较高,可以准确拾取其位置。为了准确定位初至波起跳位置,可以参照相位域起跳点估算技术[5],对计算得到的初至点进行移位。
3.2 陆上地震资料应用
对陆上二维线某单炮记录进行整体分析,效果如图9至图11。
从图9和图10可以看出,140~180道位置处的折射波能量比较强,信噪比较高,对噪声判别系数不敏感,1~35道位置处的折射波能量比较弱,初至时间随噪声判别系数的影响较大。随着噪声判别系数的增大,拾取的初至越来越靠近准确的初至时间。统计初至时间差如表9,当噪声判别系数在0.05~0.10时,震源两侧初至时间均准确。
原始地震数据的初至附近子波视周期为20个样点左右,图9b可知,当前后时窗宽度为5~50时,远偏移距折射波拾取错误,因其没有满足时窗宽度要求而出现偏差。

图9 不同噪声判别系数和不同时窗宽度初至拾取结果

图10 不同噪声判别系数初至拾取结果
表9 不同噪声判别系数初至时间差

噪声判别系数对00.010.010.020.020.030.030.040.040.050.050.060.060.070.070.080.080.090.090.10平均每道初至时间差(样点数)314.714.60041.400000
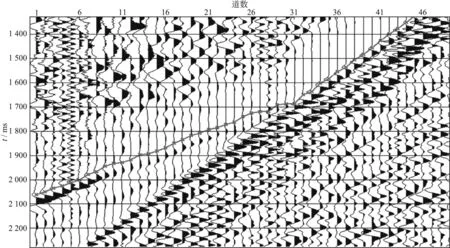
图11 初至拾取结果的局部放大
从图11可以看出,在弱能量折射波和直达波交点位置,本方法能够准确拾取地震记录初至波波谷位置,没有因强能量续至波的影响而拾取错误的初至时间。
3.3 海上地震资料应用
选取中国东部某海域的海底地震仪(OBS)采集的地震数据进行分析,通过海底地震仪采集数据的初至波,可以进行层析成像,探明地下介质的速度结构。该海底地震仪采集参数:道间距125m,总道数2501道,采样间隔4ms,记录长度10s,震源为气枪震源。选取其中的1~600道进行初至拾取。由于研究区海底地形比较复杂,所以初至波时间变化较大。
从图12a和表10可以看出,初至波波形比较复杂,随着噪声判别系数的增大,初至时间逐渐逼近准确的初至时间,当噪声判别系数为0.03~0.10时,拾取的初至时间趋于稳定。原始OBS数据初至附近子波视周期大约为20个样点。从图12b可以看出,时窗宽度为20~30个样点的初至曲线,发生了比较大的误差,随着前后时窗宽度的增大,初至时间基本上没有变化。

图12 不同噪声判别系数和不同时窗宽度初至拾取结果
表10 不同噪声判别系数初至时间差

噪声判别系数对0.00.010.010.020.020.030.030.040.040.050.050.060.060.070.070.080.080.090.090.10平均每道初至时间差(样点数)0035.6500.017000000.017
图13为原始OBS数据初至拾取结果。可以看出,初至拾取结果符合图12a所示的情况。图14 为初至拾取结果的局部放大,可以看出,在海底地形起伏比较大的情况下,本方法仍能够很好的完成初至拾取,且具有一定的抗噪能力。从近偏移距初至拾取结果(图15)可以看出,近偏移距道信噪比较高,初至拾取的精度很高。
从图16可以看出,当相邻道初至波时差变化比较大时,基于时频分析的初至拾取能够准确拾取初至,并且不会影响后续道初至拾取的准确性。
图17是远偏移距道的初至拾取结果。从图17中可以看出,存在个别噪声较大地震道的情况下,后续道的初至拾取不受影响。为了检验方法的抗噪性,将原始数据初至之前的噪声扩大了8倍,然后用同样的流程拾取初至,拾取的结果如图18和图19。

图13 OBS数据初至拾取结果(蓝色线a0=0.02,红色线a0=0.05,时窗40~80)

图14 初至拾取结果局部放大

图15 近偏移距初至拾取结果

图16 相邻道时差变化较大时的初至拾取结果

图17 远偏移距初至拾取结果
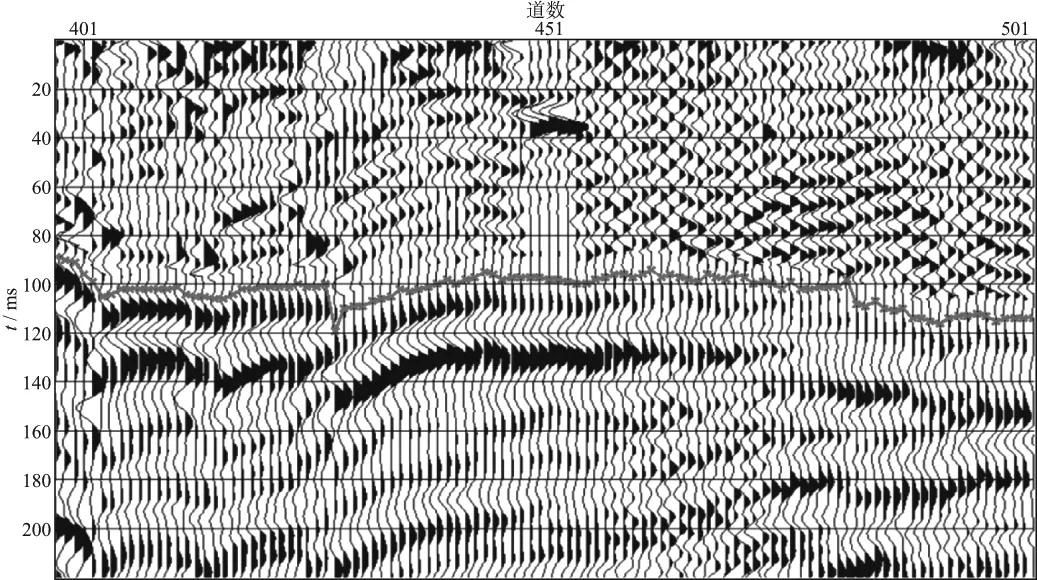
图18 原始数据噪声放大后初至拾取结果(局部)

图19 远偏移距含噪信号初至拾取结果
由图18和图19可以看到,本文提出的方法具有一定的稳定性和抗噪能力。
实际资料的应用表明,利用时频分析提取的初至,可以提高初至拾取的精度,并具有一定的抗干扰能力。
4 结论与建议
利用连续小波变换得到的地震记录的瞬时相位谱的过零点特性,拾取地震记录的初至,取得良好应用效果并得到以下结论和建议:
1) 通过小波变换时频分析得到的瞬时相位谱拾取地震波初至,在一定程度上避免了初至波能量小、续至波能量强引起的误差,并有一定的抗噪能力。
2) 当地震资料信噪比较低时,可以先将地震信号极性反转,将强能量的波峰转换成波谷,再利用该方法拾取初至位置,并利用相位域起跳点估算技术将拾取的初至移动到原始初至波波谷位置或者初至波起跳位置。
3) 本文提出的“噪声判别系数”参数的设计原则,是给定一个“噪声判别系数”范围,逐渐逼近准确初至时间,在理论上仍然需要进一步完善,最好能够根据信号本身自适应的确定每一个地震道的“噪声判别系数”;而“时窗宽度”参数比较随意,要求时窗内部包含初至波且前时窗宽度不小于半个子波视周期,后时窗宽度不小于2.5倍的子波视周期。
[1] 陈启元,王彦春,段云卿,等.复杂山区的静校正方法探讨[J].石油物探,2001,40(1):73-81 Chen Q Y,Wang Y C,Duan Y Q,et al.A study on the methods of static correction in complicated mountain area[J].Geophysical Prospecting for Petroleum,2001,40(1):73-81
[2] 陈世军,张建中.初至波射线层析成像在复杂区静校正中的应用[J].石油物探,2006,45(1):34-39 Chen S J,Zhang J Z.The application of seismic first arrival ray tracing tomography static in the complicated near surface area[J].Geophysical Prospecting for Petroleum,2006,45(1):34-39
[3] Gelchinsky B,Shtivelman V.Automatic picking of first arrivals and parameterization of traveltime curves[J].Geophysical Prospecting,1983,31(6):915-928
[4] Coppens F.First arrival picking on common-offset trace collections for automatic estimation of static
corrections[J].Geophysical Prospecting,1985,33(8):1212-1231
[5] 刘志成.初至智能拾取技术[J].石油物探,2007,46(5):521-530 Liu Z C.First break intelligent picking technique[J].Geophysical Prospecting for Petroleum,2007,46(5):521-530
[6] 曾富英,李敏锋,申维.地震波初至拾取的分形研究[J].现代地质,2002,16(2):209-213 Zeng F Y,Li M F,Shen W.The fractal study on detecting arrival time of the first break[J].Geoscience,2002,16(2):209-213
[7] 庄东海,肖春燕,颜永宁.利用人工神经网络自动拾取地震记录初至[J].石油地球物理勘探,1994,29(5):659-664 Zhuang D H,Xiao C Y,Yan Y N.Seismic first arrival pickup using artificial neural network[J].Oil Geophysical Prospecting,1994,29(5):659-664
[8] 潘树林,高磊,邹强,等.一种实现初至波自动拾取的方法[J].石油物探,2005,44(2):163-166 Pan S L,Gao L,Zou Q,et,al.An automatic method to pick up the first break time[J].Geophysical Prospecting for Petroleum,2005,44(2):163-166
[9] 刘喜武,年静波,黄文松.利用广义S变换提取地震旋回的方法[J].石油物探,2006,45(2):129-133 Liu X W,Nian J B,Huang W S.Seismic cycle extraction using generalized S-transform[J].Geophysical Prospecting for Petroleum,2006,45(2):129-133
[10] 陆基孟.地震勘探原理[M].东营:中国石油大学出版社,1993,114 Lu J M.The principle of seismic exploration[M].Dongying:China University of Petroleum Press,1993,114
[11] 韩文功,于静,张怀榜,等.干扰波调查方法在高密度地震采集中的应用[J].石油物探,2011,50(5):499-507 Han W G,Yu J,Zhang H B,et al.Application of interference wave investigation methods in high-density seismic acquisition[J].Geophysical Prospecting for Petroleum,2011,50(5):499-507
[12] 张海燕,李庆忠.几种常用解析子波的特性分析[J].石油地球物理勘探,2007,42(6):651-657 Zhang H Y,Li Q Z.Analysis on feature of common analytic wavelets[J].Oil Geophysical Prospecting,2007,42(6):651-657
[13] 李庆忠.走向精确勘探的道路[M].北京:石油工业出版社,1993,134 Li Q Z.The way to obtain a better resolution in seismic prospecting[M].Beijing:Petroleum Industry Press,1993,134
(编辑:朱文杰)
First-break picking based on time-frequency analysis
Yue Long,Liu Huaishan,Liu Kai,Xu Xiugang,Xing Lei
(KeyLabofSubmarineGeosciencesandProspectingTechniques,MinistryofEducation,OceanUniversityofChina,Qingdao266100,China)
The first-break picking is a basic work of seismic data processing,especially the static correction and tomography imaging requires accurate first-break time.When the primary wave arrives,the amplitude,frequency and phase of the signals will change.Based on the above recognition,a new first-break picking algorithm is put forward based on time-frequency analysis.Under the constraint of noise discrimination coefficient,time-frequency analysis is conducted by wavelet transform to extract the instantaneous phase spectrum of signals,and then pick up the first-break using the zero-crossing point attribute of instantaneous phase spectrum.In order to improve the computational efficiency,the instantaneous phase spectrum of signals is calculated within a pre-defined time window and the statistical results of several first-break results of different noise discrimination coefficients are used to determine the final first-break time.Theory signals and real seismic data examples show that the approach owns higher noise-resistance and precision.
first-break picking,wavelet transform,time-frequency analysis,instantaneous phase spectrum,noise discrimination coefficient
2015-02-06;改回日期:2015-05-04。
岳龙(1988—),男,博士在读,主要从事地震资料处理方法研究工作。
邢磊(1984—),男,讲师,主要从事海洋地球物理勘探研究工作。
国家自然科学基金项目(41176077和41230318)和国家高技术研究发展计划(863计划)项目(2013AA092501)联合资助。
P631
A
1000-1441(2015)05-0508-13
10.3969/j.issn.1000-1441.2015.05.004
