球面波PP反射系数的频变特征研究

李京南， 王尚旭*， 董春晖， 袁三一， 王静波

1 中国石油大学(北京)油气资源与探测国家重点实验室, 北京　102249 2 中国石油大学(北京)CNPC物探重点实验室, 北京　102249 3 中国石油化工股份有限公司勘探分公司, 成都　610041



球面波PP反射系数的频变特征研究

李京南1,2， 王尚旭1,2*， 董春晖1,2， 袁三一1,2， 王静波3

1 中国石油大学(北京)油气资源与探测国家重点实验室, 北京102249 2 中国石油大学(北京)CNPC物探重点实验室, 北京102249 3 中国石油化工股份有限公司勘探分公司, 成都610041

与平面波反射系数相比，球面波反射系数可以更精确地描述实际地震波的反射特征.近些年关于球面波的研究主要聚焦于球面波反射系数随入射角的变化规律，很少对球面波反射系数随频率的变化(频变)做详细研究.为了更全面地了解球面波的反射机制，本文研究了两层弹性介质中球面波PP反射系数(幅值和相位)的频变规律.文中基于经典的Sommerfeld积分构造球面波PP反射系数，通过自适应的Gauss-Kronrod求积算法对其进行稳定的数值计算.数值试验发现，对于不同的介质参数，球面波反射系数表现出了复杂的频变规律.尤其是当平面波反射系数为零时，对应的球面波反射系数是非零的，且球面波反射系数的相位随频率增加在高频趋近于90°或-90°，即此时球面反射波相对于入射波会有90°的相位旋转.对四类AVO模型的测试表明，球面波反射系数与平面波反射系数在临界角附近和低频时差异很大.

球面波； 平面波； 反射系数； 频变

1　引言

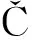
近十年来，关于反射球面波的研究再次引起了地球物理学家的注意，研究内容主要聚焦于大偏移距的球面波AVO特征分析和AVO参数反演.这些研究的前提需要计算球面波反射系数，其计算方法大致可以分为两类：一类是通过Sommerfeld积分构建反射系数并对其进行数值计算(Haase, 2004; Ursenbach et al., 2007; 黄饶等, 2009)；另一类是利用反射率法或有限差分法进行全波场地震模拟来求取反射系数(印兴耀等, 2006; Alhussain et al., 2008; Zhu and McMechan, 2012; 杨心超, 2012).研究发现在临界角附近平面波反射系数和球面波反射系数之间存在很大的差异，此时平面波理论是失效的.鉴于此，Alhussain等(2008)，Skopintseva等(2011)，Zhu和McMechan(2012)利用球面波反射系数进行AVO反演，与常规的基于平面波反射系数的AVO反演相比，反演结果得到了显著的改善.

上述研究主要是利用大入射角度的球面波反射系数随入射角变化的特征，未对球面波反射系数与频率的关系做深入分析.根据经典的几何地震学，平面波反射系数是与频率无关的，但球面波反射系数是随频率变化(频变)的.忽略球面波反射系数的频变特征可能会导致不精确的、甚至错误的地下构造解释，尤其是对于浅层、低频率和反射界面曲率很大的情况.因此，为了更精确地描述实际地震波的反射特征、充分利用地震数据含有的有用信息，对球面波反射系数频变特征进行研究具有重要的意义.

目前并没有论文和著作阐述弹性介质中球面波反射系数的频变机制.本文对两层半无限大弹性介质中球面波PP反射系数的频变特征进行系统地研究，并与平面波反射系数进行对比.文中首先基于Sommerfeld积分建立球面波PP反射系数的积分表达式，采用自适应的Gauss-Kronrod求积算法(Shampine, 2008)对其进行稳定的数值计算.然后通过数值测试揭示球面波PP反射系数复杂的频变特征，并对频变特征进行分类.最后讨论该研究的意义.

2　方法原理

对于图1所示的两均匀半空间弹性介质模型，当激发的P波震源位于上层介质时(图1中的S点)，根据Aki和Richards (1980)，在接收位置P处的球面反射P波位函数可表示为

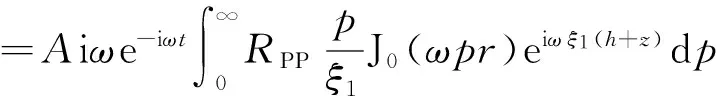
(1)

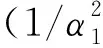
图1　本文研究的两层介质模型的观测系统.S和S*为点震源及其对应的虚震源，P是检波器位置.实线表示P波，虚线表示SV波Fig.1　Observation system of the two-layer model investigated in this study. S and S* are point source and the corresponding image source, respectively; P is a recording position. Solid lines represent P waves and dashed lines represent SV waves.

其中，ρ1和ρ2分别为上层和下层介质的密度，β1和β2分别为上层和下层介质的SV波速度，α2为下层介质的P波速度，i2是P波的透射角度，j1和j2分别是SV波的反射角度和透射角度.

球面反射P波的位移与位函数有如下关系

(3)其中，ur和uz分别为反射P波沿径向和垂直方向的位移分量.

本文考虑反射P波沿射线方向的位移分量，可表示为

uref=ursinθ+uzcosθ

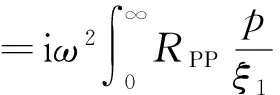
×eiω ξ1(h+z)dp,

(4)

其中，J1是一阶贝塞尔函数，θ为射线入射角，注意这个角度为真实的入射角度，上述的i1为积分变量中的入射角.

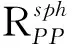
(5)由于虚源入射波的位函数可以解析地表示为

(6)则虚源入射波沿射线方向的位移可以容易地得到

(7)其中，R=(h+z)/cosθ，即地震波由震源出发到接收点的传播距离.

将(4)和(7)代入(5)式，则有

(8)

(8)式的积分路径中含有奇点p=1/α1，这给数值计算带来了困难.参考Ursenbach等(2007)的做法，通过如下的变量代换来消除奇点：p=sini1/α1，ξ1=cosi1/α1，于是有(p/ξ1)dp=-d(cosi1)/α1，cosi1∈[1,0]∪[0,i∞].将上述代换代到(8)中，并令x=cosi1，经过一系列推导和整理，最后可以得到球面反射P波的位移反射系数为

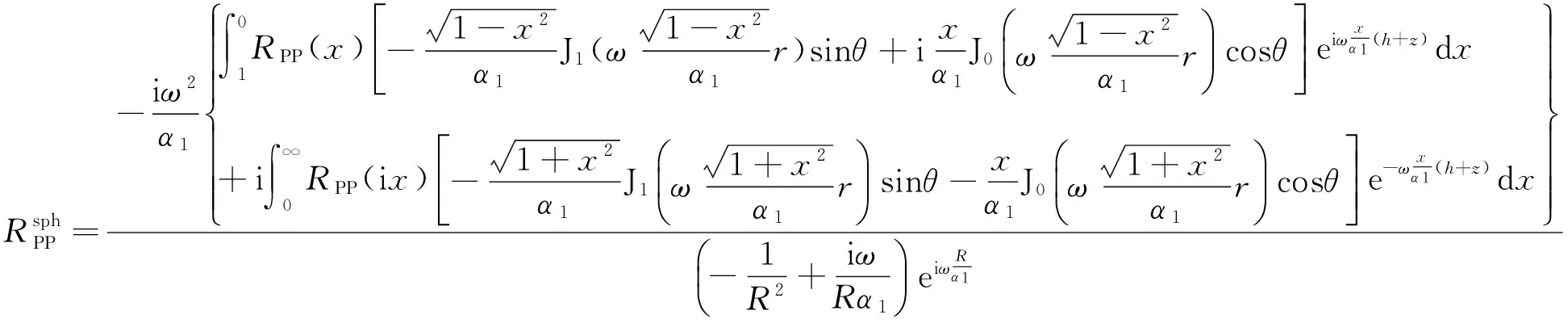
(9)

根据Snell定理，可用sini1表示(2)式中的cosi2、cosj1、cosj2和p，再用cosi1表示sini1，由于x=cosi1，最后便可以获得(9)式中的RPP(x).

3　数值结果及分析

3.1球面波反射系数的频变规律

为深入探讨球面波PP反射系数的频变规律，下面针对不同的参数模型绘制其随频率的变化曲线并归纳分析.这里只考虑临界角前较小的入射角度.

对各种参数模式的频变规律进行了数值测试，从测试结果中选取两个典型的例子进行说明，即α1<α2和α1>α2两种情况，如表1所示.其他参数为h=500 m，z=500 m，入射角以0°为例.图2和图3分别为当α1<α2和α1>α2时的球面波PP反射系数频变曲线.为了便于比较不同参数时球面波反射系数的频变规律，对反射系数幅值进行规零化，即用球面波和平面波反射系数的幅值与对应的平面波反射系数幅值的差值作为纵轴，如图2a、3a所示，|Rsw|、|Rpw|分别表示球面波反射系数和平面波反射系数的幅值，则不同介质参数的平面波反射系数都由黑色虚线表示；反射系数的相位不做处理，如图2b、3b所示.从图2和图3中可以看出，对于不同的介质参数，球面波PP反射系数的频变规律是很复杂的，通过详细地研究分析，可以归纳总结为如下.

表1　测试模型参数Table 1　Parameters of tested models

当α1<α2时(见图2).

1) 当ρ1=2.50 g·cm-3时，平面波反射系数为零，而球面波反射系数是非零的，且其幅值随频率增加而单调递减，并在高频趋近于平面波反射系数的幅值；球面波反射系数的相位随着频率增加而减小，并在高频趋近于90°，这说明球面反射P波与入射波有90°的相位差.这一现象尚未在目前的文献中见诸.

2) 当ρ1=2.42 g·cm-3时，平面波反射系数为较小的正数(0.0163)，球面波反射系数的幅值在很低频率处大于平面波反射系数，但在其他的频率小于平面波反射系数，且随频率增加而在高频趋近于平面波反射系数的幅值；球面波反射系数的相位随频率增加从一个较大的相位值(约120°)单调递减地趋近于平面波反射系数的相位(0°).当ρ1=1.90 g·cm-3时，平面波反射系数为较大的正数(0.1364)，球面波反射系数的幅值小于平面波反射系数的幅值，且随频率增大而增大并在高频趋近平面波反射系数的幅值；球面波反射系数的相位随频率增加从一个较小的相位值(约40°)逐渐趋近平面波反射系数的相位(0°).

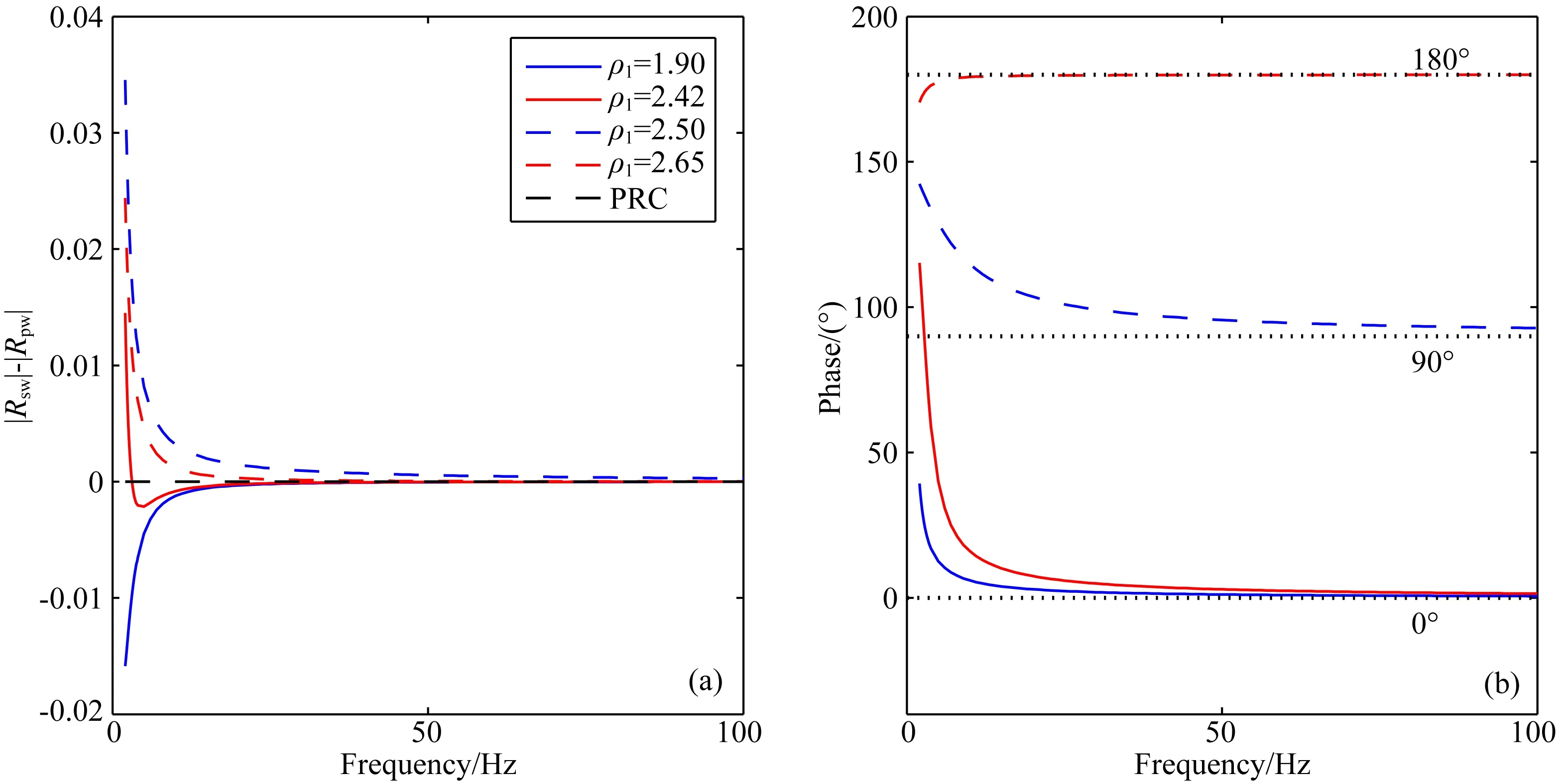
图2　α1<α2时球面波PP反射系数幅值(a)和相位(b)的频变规律α1=2000 m·s-1, α2=2500 m·s-1, ρ2=2 g·cm-3. Fig.2　Frequency-dependent characteristics of spherical-wave PP reflection coefficient when α1<α2. Magnitude (a) and phase (b)

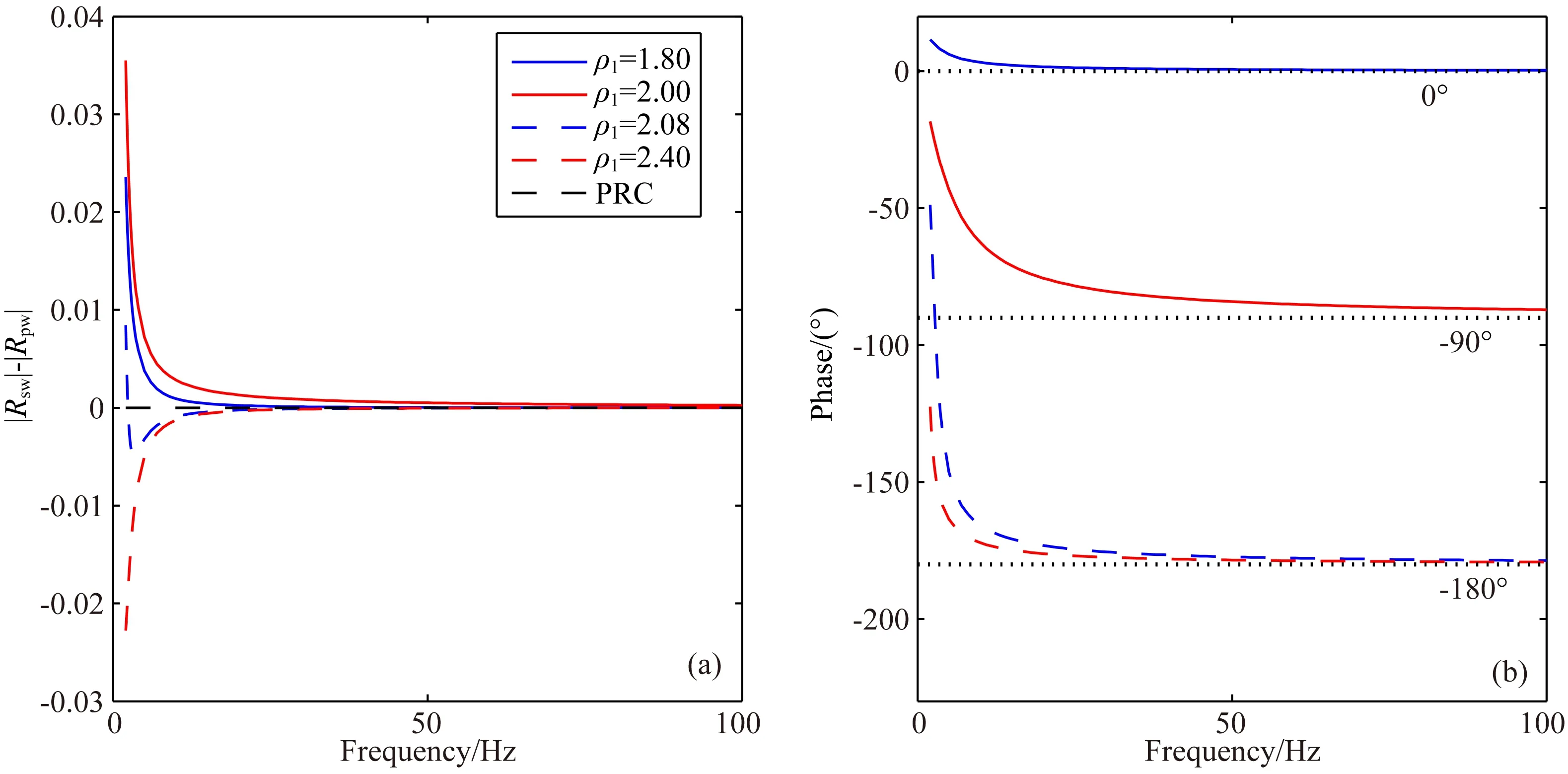
图3　α1>α2时球面波PP反射系数幅值(a)和相位(b)的频变规律α1=2500 m·s-1, α2=2000 m·s-1, ρ2=2.5 g·cm-3.Fig.3　Frequency-dependent characteristics of spherical-wave PP reflection coefficient when α1>α2. Magnitude (a) and phase (b)

3) 当ρ1=2.65 g·cm-3时，平面波反射系数为负数(-0.0291)，球面波反射系数幅值总是大于对应的平面波反射系数幅值，且随频率增加而单调递减，并在高频趋近平面波反射系数的幅值；球面波反射系数的相位与平面波反射系数的相位在低频处有较小的差异，且随频率增加两者变得几乎相等(由于此时平面波反射系数为负数，其相位为180°).

当α1>α2时(见图3).

1) 当ρ1=2.00 g·cm-3时，平面波反射系数为零，但球面波反射系数是非零的，且其幅值随频率增加而单调递减，并在高频趋近于平面波反射系数的幅值；球面波反射系数的相位随着频率增加而减小，并在高频趋近于-90°，这说明球面反射P波与入射波相比有90°的相位旋转.

2) 当ρ1=2.08 g·cm-3时，平面波反射系数为绝对值较小的负数(-0.0196)，球面波反射系数的幅值在低频处大于平面波反射系数，但在其他的频率小于平面波反射系数，且随频率增加在高频趋近平面波反射系数的幅值；球面波反射系数的相位随频率增加从约-50°单调递减地趋近平面波反射系数的相位(-180°).当ρ1=2.40 g·cm-3时，平面波反射系数为绝对值较大的负数(-0.0909)，球面波反射系数的幅值随频率增大而单调递增并在高频趋近平面波反射系数的幅值；球面波反射系数的相位随频率增加而减小，并在高频趋近平面波反射系数的相位.

3) 当ρ1=1.80 g·cm-3时，平面波反射系数为正数(0.0526)，球面波反射系数幅值总是大于对应的平面波反射系数，且随频率增加而单调递减，并在高频趋近平面波反射系数的幅值；球面波反射系数的相位与平面波反射系数的相位在低频处有较小的差异，且随频率增加两者的差异逐渐减小，并在较高频率趋于相等.

从上述研究中可以看出，球面波反射系数是频变的，平面波反射系数是非频变的.需要特别说明的是，平面波反射系数是非频变的只是针对均匀平面波而言.实际上，非均匀平面波是频变的.Sommerfeld积分将球面波分解为均匀平面波和非均匀平面波的叠加，正是由于非均匀平面波的频变，导致了最后叠加得到的球面反射波是频变的，因此球面波反射系数是频变的.

3.2单频的AVO特征

这部分以AVO分析为例探讨球面波反射系数频变特征的应用.AVO分析广泛应用于地震勘探中，但通常基于平面波理论，如基于Zoeppritz方程或其线性近似.然而平面波理论预测的反射系数在临界角附近是失效的，这促使人们开始关注更接近真实情况的球面波的AVO响应.典型地，Haase(2004)、Alhussain等(2008)、李胜军等(2012)研究了球面PP波反射系数随入射角的变化规律，但其主要是在时间域求取球面波反射系数，即分析的是带限球面波反射系数随入射角变化的特征.为了研究单频的球面波AVO特征，这里根据(9)式计算不同频率时球面谐波反射系数随入射角变化的曲线，进而分析频率对球面波AVO特征的影响.

测试了四类AVO模型，其中第一、二类模型根据Haase(2004)所用的模型做了小的修改，第三、四类模型为Castagna等(1998)所用的模型，具体参数如表2所示.其他的参数为h=500 m,z=500 m, 入射角范围为0～80°.根据上述方法分别计算四类模型参数在地震频段内三个频率5 Hz、30 Hz和80 Hz(分别代表低频、中频、高频)时的球面波反射系数随入射角变化的曲线，为便于比较，也给出了根据(2)式计算的平面波反射系数随入射角变化的曲线，如图4—7所示，其中PRC代表平面波反射系数.对比四个图可以发现，第一、二类AVO的幅值和相位都有较大的频变；第三、四类AVO的幅值有很小的频变，相位的频变也较小.

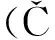
表2　第1—4类AVO模型参数Table 2　Parameters of Class 1—4 AVO models

图4　第一类AVO，PP反射系数幅值(a)和相位(b)随入射角的变化Fig.4　Class 1 AVO, PP reflection coefficient magnitude (a) and phase (b) variation with incident angles

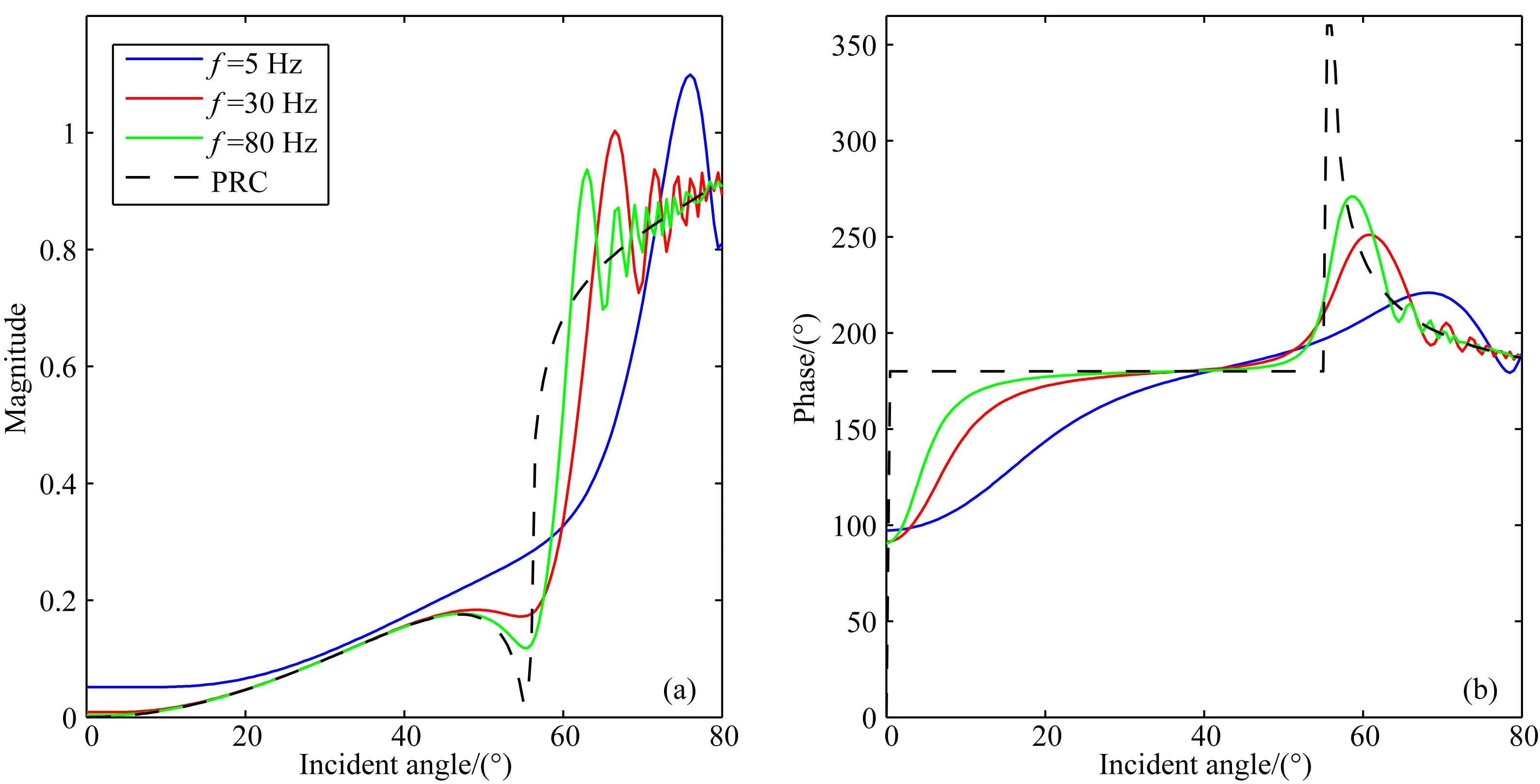
图5　第二类AVO，PP反射系数幅值(a)和相位(b)随入射角的变化Fig.5　Class 2 AVO, PP reflection coefficient magnitude (a) and phase (b) variation with incident angles

图6　第三类AVO，PP反射系数幅值(a)和相位(b)随入射角的变化Fig.6　Class 3 AVO, PP reflection coefficient magnitude (a) and phase (b) variation with incident angles

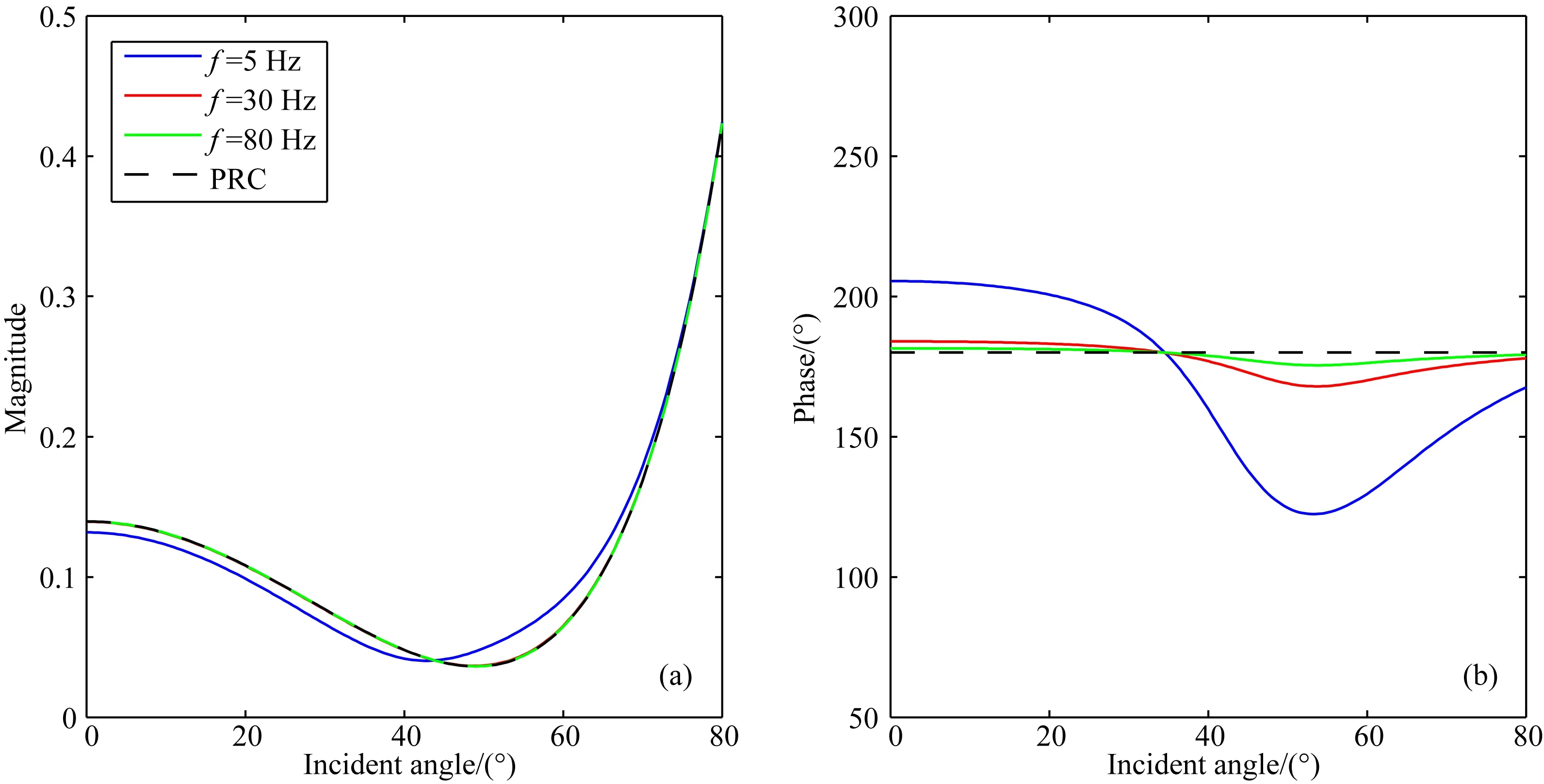
图7　第四类AVO，PP反射系数幅值(a)和相位(b)随入射角的变化Fig.7　Class 4 AVO, PP reflection coefficient magnitude (a) and phase (b) variation with incident angles

对于第三、四类AVO模型，如图6和图7所示，在这两种模型参数下不会产生首波，因此AVO曲线都比较光滑，没有出现在第一、二类AVO情况下临界角后的振荡现象.中高频(30 Hz和80 Hz)球面波反射系数的幅值和平面波反射系数的幅值差异很小，几乎是相等的；低频时(5 Hz)球面波反射系数幅值与平面波反射系数幅值之间有较小的差异.另外，不同频率的球面波反射系数的相位与平面波反射系数的相位之间存在一定的差异，且频率越小这种差异越大，尤其是对于低频，在某些入射角两者差异较大.总的来说，频率对第三、四类AVO模型的球面波AVO响应的影响较小，只有当频率很低时这种影响才相对较大.

综上所述，对于四类AVO模型，球面波反射系数与平面波反射系数在临界角附近或低频时差异很大.因此在临界角附近或低频时，需要考虑球面波反射的频变效应.

4　讨论

从上述的数值测试(图2和图3)中可以发现，球面波PP反射系数的频变规律是很复杂的.对于上述的两种典型情况(α1<α2和α1>α2)，球面波PP反射系数幅值的频变规律大体是一致的，其相位的频变规律存在较小的差异(比较图2b和3b).尤其地，当平面波PP反射系数为零时，球面波PP反射系数却是非零的，且球面波反射系数的相位随频率增加在高频趋近于90°或-90°.值得注意的是，这种现象在基于平面波理论的几何地震学中是不会发生的，这丰富了我们对波传播规律的认识.按照几何射线理论或平面波理论，当平面波入射到界面上某一点后，根据Snell定理，其反射只对应着一条确定的射线路径.但是根据Sommerfeld积分，球面波可以分解为平面波的叠加，具体地说，球面波入射到界面上某一点后的反射，可以看作是围绕着中心射线的一束射线对应的平面波反射的加权叠加(Alhussain et al., 2008)，这束射线中的每一条射线都有不同的入射角度，并且都满足Snell定理.因此尽管图2和图3的测试中射线角度是0°，但球面反射波却是包含0°在内的一定范围入射角的平面反射波的叠加，对于图2中蓝色虚线或图3中红色实线对应的参数，非零度的平面波反射系数是非零的，故最后得到的球面波反射系数也是非零的.

球面波反射系数的频变规律可以带给我们很多启发性的思考.首先，这一发现可以丰富我们对地震波反射机制的认识，有助于更好地了解实际地下介质中地震波的传播规律.通过测试可以看出球面波PP反射系数的频变规律在低频、浅层尤为显著，因此其对于近地表球面波传播及反射规律的研究更有帮助；另外，近些年来随着低频勘探技术的发展，现已可采集到低至1.5 Hz的地震数据(Wang et al., 2013)，在如此低的频率下球面波的频变效应将会很明显，更精确的勘探需要考虑球面波反射系数的频变.另一方面，球面波反射系数的频变特征与地下介质参数是紧密相关的，利用其可能为反演地下介质的弹性参数提供一种新的思路，可以参考王静波(2014)利用球面声波反射系数进行反演的思路，基于(9)式用全局反演方法来反演介质的弹性参数.关于球面波反射系数频变特征的具体应用需要进一步地研究.

5　结论

本文根据Sommerfeld积分公式建立了两层弹性介质中球面波PP反射系数的积分表达式，基于此研究分析了不同参数情况下球面波PP反射系数的频变特征，并对其总结分类；探讨了四类AVO模型的单频球面波反射系数随入射角的变化规律.概括地，得到了以下几方面的结论和认识.

1) 当α1<α2、平面波反射系数为较大的正数或当α1>α2、平面波反射系数为绝对值较大的负数时，球面波反射系数幅值小于平面波反射系数幅值，并随频率的增加而增大，在高频趋于平面波反射系数；球面波反射系数相位大于平面波反射系数相位，且随频率增加而减小，在高频趋于平面波反射系数相位.

2) 当α1<α2、平面波反射系数为较小的正数或当α1>α2、平面波反射系数为绝对值较小的负数时，球面波反射系数幅值在很低频率时大于平面波反射系数幅值，在其他频率时小于平面波反射系数幅值，并随频率的增加在高频趋于平面波反射系数；球面波反射系数相位大于平面波反射系数相位，且随频率增加而减小，在高频趋于平面波反射系数相位.

3) 无论α1<α2还是α1>α2，当平面波反射系数为零时，球面波反射系数不为零：球面波反射系数幅值大于平面波反射系数幅值，并随频率的增加而减小，在高频趋于平面波反射系数；球面波反射系数的相位随频率增加在高频趋近于90°或-90°.

4) 当α1<α2、平面波反射系数为负数或当α1>α2、平面波反射系数为正数时，球面波反射系数幅值大于平面波反射系数幅值，并随频率的增加而减小，在高频趋于平面波反射系数；球面波反射系数相位与平面波反射系数相位在低频时有较小差异，且随频率增加两者趋于相等.

5) 对于第一、二类AVO模型，球面波反射系数与平面波反射系数在临界角附近和低频时差异都很大；对于第三、四类AVO模型，球面波反射系数与平面波反射系数仅在频率很低时才有相对大的差异.

致谢感谢休斯顿大学黄龙博士对论文撰写提供的帮助.

Aki K, Richards P G. 1980. Quantitative Seismology: Theory and Methods, Vol. 1. San Francisco, CA: W. H. Freeman & Co.

Alhussain M, Gurevich B, Urosevic M. 2008. Experimental verification of spherical-wave effect on the AVO response and implications for three-term inversion.Geophysics, 73(2): C7-C12.

Alulaiw B, Gurevich B. 2013. Analytical wavefront curvature correction to plane-wave reflection coefficients for a weak-contrast interface.GeophysicalProspecting, 61(1): 53-62.

Brekhovskikh L M. 1980. Waves in Layered Media. New York: Academic Press.

Brekhovskikh L M, Godin O A. 1999. Acoustics of Layered Media II, Point Sources and Bounded Beams. 2nd ed. Berlin Heidelberg: Springer. Castagna J P, Swan H W, Foster D J. 1998. Framework for AVO gradient and intercept interpretation.Geophysics, 63(3): 948-956.

Du S T, Yu K Y. 1985. Lecture notes on the theory of seismic wave dynamics (in Chinese). Dongying: Geophysical Exploration Department of East China Petroleum Institute.

Haase A B. 2004. Spherical wave AVO modeling of converted waves in isotropic media. ∥ 74thSEG Annual Meeting. Denver, Colorado: SEG, 263-266.

Huang R, Chen X H, Li J Y. 2009. Seismogram synthesis method based on spherical wave and AVO analysis.JournalofChinaUniversityofPetroleum(EditionofNaturalScience) (in Chinese), 33(3): 49-52.

Li S J, Gao J H, Yong X S, et al. 2012. Spherical-wave AVO analysis of reflected P-wave.ChineseJ.Geophys. (in Chinese), 55(10): 3459-3466, doi: 10.6038/j.issn.0001-5733.2012.10.029. Shampine L F. 2008. Vectorized adaptive quadrature in Matlab.J.Comput.Appl.Math., 211(2): 131-140.

Skopintseva L, Ayzenberg M, LandrM, et al. 2011. Long-offset AVO inversion of PP reflections from plane interfaces using effective reflection coefficients.Geophysics, 76(6): C65-C79.

Sommerfeld A. 1909. über die Ausbreitung der Wellen in der drahtlosen Telegraphie.AnnalenderPhysik, 333(4): 665-736.

Ursenbach C P, Haase A B, Downton J E. 2007. Efficient spherical-wave AVO modeling.TheLeadingEdge, 26(12): 1584-1589.

Wang J B. 2014. Frequency-dependence of spherical-wave reflection and transmission coefficients: Analysis and Application [Ph. D. thesis] (in Chinese). Beijing: China University of Petroleum (Beijing).

Wang J F, Ma T, Liu Z G, et al. 2013. A new method to extend the range of low-frequency vibroseis sweeps. ∥ 83rdAnnual Meeting. Houston, Texas: SEG, 254-258.

Weyl H. 1919. Ausbreitung elektromagnetischer Wellen über einem ebenen Leiter.AnnalenderPhysik, 365(21): 481 -500.

Xu J X, Wu L. 1997. The theoretical study of the elastic wave: on the first term of spherical wave.GeophysicalProspectingforPetroleum(in Chinese), 36(1): 1-12. Yang X C. 2012. Study of characteristics of spherical-wave reflection coefficients [M. S. thesis] (in Chinese). Beijing: China University of Petroleum (Beijing).

Yin X Y, Zhao J, Zhang F C, et al. 2006. Method of generating prestack synthetic seismograms of spherical wave.JournalofChinaUniversityofPetroleum(EditionofNaturalScience) (in Chinese), 30(1): 26-32.

Zhu X F, McMechan G A. 2012. Elastic inversion of near- and postcritical reflections using phase variation with angle.Geophysics, 77(4): R149-R159.

附中文参考文献

杜世通, 俞康胤. 1985. 地震波动力学理论讲义. 东营: 华东石油学院物探教研室.

黄饶, 陈小宏, 李景叶. 2009. 基于球面波的地震记录合成方法及AVO分析. 中国石油大学学报(自然科学版), 33(3): 49-52.

李胜军, 高建虎, 雍学善等. 2012. 球面波的反射P波AVO分析. 地球物理学报, 55(10): 3459-3466, doi: 10.6038/j.issn.0001-5733.2012.10.029.

王静波. 2014. 球面波反射和透射系数频变特征分析与应用[博士论文]. 北京: 中国石油大学(北京).

徐基祥, 吴律. 1997. 弹性波理论研究—关于球面波首项(Ⅰ). 石油物探, 36(1): 1-12.

杨心超. 2012. 球面波反射系数特征研究[硕士论文]. 北京: 中国石油大学(北京).

印兴耀, 赵剑, 张繁昌等. 2006. 球面波叠前地震记录的合成方法. 中国石油大学学报(自然科学版), 30(1): 26-32.

(本文编辑胡素芳)

Study on frequency-dependent characteristics of spherical-wave PP reflection coefficient

LI Jing-Nan1, 2, WANG Shang-Xu1, 2*, DONG Chun-Hui1, 2, YUAN San-Yi1, 2, WANG Jing-Bo3

1StateKeyLaboratoryofPetroleumResourceandProspecting,ChinaUniversityofPetroleum(Beijing),Beijing102249,China2CNPCKeyLabofGeophysicalExploration,ChinaUniversityofPetroleum(Beijing),Beijing102249,China3SinopecExplorationCompany,Chengdu610041,China

Spherical-wave reflection coefficient (SRC) describes the seismic wave reflection more precisely and realistically than the plane-wave reflection coefficient (PRC). This study mainly focuses on the frequency-dependent characteristics of SRC, which are usually not considered. To better understand the reflection mechanism of spherical waves, we systematically investigate the frequency-dependent characteristics of SRC (P-wave only) in a two-layer elastic medium model with a planar interface. We use the classical Sommerfeld integral to construct the SRC and compute it with adaptive Gauss-Kronrod quadrature. Numerical simulations show that for different media with various properties, the frequency-dependence of SRC exhibits very complicated responses. Significant deviations between SRC and PRC are observed at low frequencies. Especially when the PRC is zero, the corresponding SRC is non-zero; with increasing frequency, the phase of the SRC approaches +90° or -90°, meaning a 90° phase rotation after reflection. Tests on Class 1-4 AVO models suggest that large discrepancy between SRC and PRC exists in the vicinity of the critical angle and at low frequencies.

Spherical wave; Plane wave; Reflection coefficient; Frequency dependent

10.6038/cjg20161025.

国家重点基础研究发展计划(973计划)项目(2013CB228600)和国家自然科学基金(41304108)联合资助.

李京南，男，1988年生，博士研究生，主要从事地震波传播、地震资料处理方面的研究.E-mail：li.jnan@163.com

王尚旭，教授，博士生导师，主要从事地震波传播理论、岩石物理、地震波正演模拟及反演研究.E-mail：wangsx@cup.edu.cn

10.6038/cjg20161025

P631

2016-03-17，2016-07-23收修定稿

李京南， 王尚旭， 董春晖等. 2016. 球面波PP反射系数的频变特征研究. 地球物理学报，59(10):3810-3819,

Li J N, Wang S X, Dong C H, et al. 2016. Study on frequency-dependent characteristics of spherical-wave PP reflection coefficient.ChineseJ.Geophys. (in Chinese),59(10):3810-3819,doi:10.6038/cjg20161025.