基于CALPHAD方法的多元合金杨氏模量的计算
2015-10-13王翠萍林明娜韩佳甲张锦彬黄艺雄刘兴军
王翠萍,林明娜,韩佳甲,施 展,张锦彬,黄艺雄,刘兴军
(厦门大学材料学院,福建厦门361005)
基于CALPHAD方法的多元合金杨氏模量的计算
王翠萍,林明娜,韩佳甲,施 展,张锦彬,黄艺雄,刘兴军*
(厦门大学材料学院,福建厦门361005)
基于纯金属杨氏模量的实验信息,本研究对纯金属的杨氏模量随温度变化的半经验模型中的参数进行了优化.借鉴相图计算的CALPHAD(calculation of phase diagram)方法,构建了多元合金杨氏模量计算的模型.基于二元合金的杨氏模量实验信息,对Fe-Ni和Ta-Mo二元系的杨氏模量计算参数进行了优化,计算了合金在不同温度和成分时的杨氏模量,计算结果与实验数据取得了良好的一致性.基于二元合金的优化参数,运用三元合金的计算模型,预测了Ta-Nb-W和Ta-Nb-Mo在不同温度和成分时的杨氏模量.
杨氏模量;CALPHAD方法;合金
杨氏模量是描述固体材料弹性形变和抵抗外力作用的表征力学性质的重要物理量[1],是材料性能研究中重要的力学参量.通过实验测量杨氏模量的主要方法有:静态测量法和动态测量法[2].由于静态测量法拉伸时载荷大,加载速度慢,对材料有一定的损坏,且所用仪器设备体积大,移动困难,同时还受材质的限制.动态测量需要有专用仪器,实验精度要求高,对实验设备的要求也高.原则上,基于密度泛函理论的第一性原理计算[3]已经能够预测很多问题,但计算工作量太大,当原子数目较多时,计算速度较慢甚至难以完成.因此,建立理论经验模型计算材料的杨氏模量是一项重要的基础理论研究工作,具有重要的应用价值.Clerc[4]提出理论模型并计算了二元合金随成分变化的剪切模量和体模量,但是该模型只计算了部分成分范围内的弹性模量.王小丽[5]以Vegard定律、简谐理论和胡克定律为基础,提出了二元理想固溶体体弹性模量计算的线性模型、简谐模型和力常数模型,但计算结果与实验数据相对误差较大.
刘兴军等[6]运用双原子模型推导的半经验模型,结合材料已有的线膨胀系数实验数据计算了部分纯金属的杨氏模量.Wachtman等[7]提出了杨氏模量随温度变化的经验模型,并将该模型运用于多种物质的计算,结果与实验数据有较好的吻合.Aderson[8]则从物理基础推导了该模型,证明了该模型的可靠性与有效性.因此,Wachtman等[7]的模型是目前较准确的模型.本研究将Wachtman等[7]提出的模型应用于计算纯金属杨氏模量随温度的变化关系.
相图计算是热力学理论和计算技术相结合的产物.基于各相热力学模型,并结合实验数据,形成并发展了相图计算技术[9-10].刘兴军等[6]借鉴相图计算的CALPHAD(calculation of phase diagram)方法较好地计算预测了部分二元合金的杨氏模量.本研究借鉴相图计算的CALPHAD方法的研究思路,构建多元合金杨氏模量计算模型,并验证了该模型的可靠性.利用该模型,基于非线性最小二乘法理论方法和多元合金杨氏模量实验结果,优化模型中的杨氏模量计算参数,计算预测了二元合金体系及三元合金体系在不同温度、成分时的杨氏模量.
1 计算方法
1.1 纯金属的杨氏模量
Wachtman等[7]提出了有温度依存性的半经验模型公式:

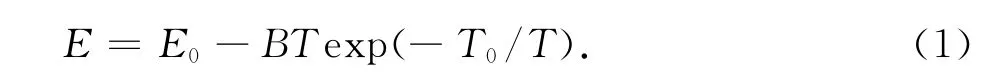
式(1)中,E是杨氏模量;E0为绝对零度下的杨氏模量;T为绝对温度;B为取决于材料的参数;T0为与德拜温度有关的参数,本研究中取为德拜温度的值.本研究基于现有纯金属的杨氏模量随温度变化的实验信息,采用非线性最小二乘法拟合,得到模型中参数E0和B的值.
为了由稳定结构的纯金属的杨氏模量,计算其他亚稳结构的纯金属的杨氏模量.根据金属杨氏模量和熔点的经验关系式[11]:

式(2)中,E为材料的杨氏模量,Tm为材料的熔点绝对温度,k是波尔兹曼常数,Ω为原子或分子体积.对于不同结构的同一纯金属,得到:

通过式(3)和式(4),可以得到不同结构的纯金属的杨氏模量之间的关系:

式(5)中Eα随温度的变化关系从模型式(1)计算得到.基于SGTE(Scientific Group Thermodata Europe)纯组元热力学数据库[12],运用CALPHAD方法,不同结构纯金属的熔点Tm可以通过金属的液相吉布斯自由能(GL)曲线和固相吉布斯自由能(GS)曲线的交点温度得到.
1.2 二元合金的杨氏模量
借鉴CALPHAD方法的研究思路,本研究构建了计算二元合金在不同温度、成分时的杨氏模量模型.其具体表达式如下:

式中EA、EB分别是组元A、B在温度T时的杨氏模量,可从纯金属的半经验模型式(1)中求得;xA、xB分别代表组元A、B的摩尔分数;IAB为此二元合金的杨氏模量计算参数.
杨氏模量计算参数IAB为成分和温度的函数,其表达式如下:

式(7)中a0、b0、c0、a1、b1、c1为待优化的参数,计算过程中采用麦夸特法(Levenberg-Marquardt)和通用全局优化法(universal global optimization,UGO),收敛判断标准设为1.00×10-20.
1.3 三元合金的杨氏模量
基于各个二元系杨氏模量计算参数,借鉴CALPHAD方法构建的三元合金杨氏模量计算模型为如下形式:
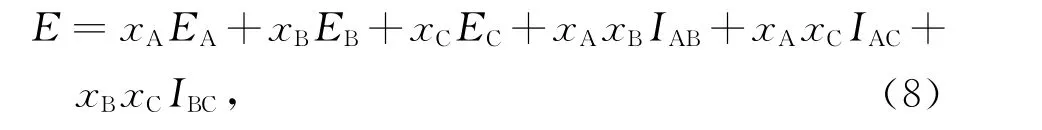
式中,EA、EB、EC分别是组元A、B、C在温度T时的杨氏模量;xA、xB、xC分别代表组元A、B、C的摩尔分数,且xA+xB+xC=1;IAB、IAC、IBC是相应二元系合金的杨氏计算参数,可由1.2部分计算得到.
2 计算结果与讨论
2.1 纯金属杨氏模量的计算
本研究中的纯金属主要是过渡族金属,Fe、Mo、Ta、W的实验数据来源于Köster[13]报道的实验信息,Ni的实验数据从Tanji等[14]的报道中得到,Nb的实验数据从Farraro等[15]的研究中获得,Ir、Pt的实验数据来源于Merker等[16]的研究工作.T0的值取自于文献中的德拜温度数据[17](见表1).基于实验信息,采用非线性最小二乘法拟合,对于半经验模型式(1)中的参数进行优化得到了E0和B的值如表1所示.

表1 纯金属的优化参数Tab.1 The optimized parameters of pure metals
图1(a)~(e)所示为体心立方结构纯金属Fe、Nb、Mo、Ta、W的杨氏模量计算结果与实验值的比较,图1(f)~(h)所示为面心立方纯金属Ni、Ir、Pt的杨氏模量计算结果与实验值的比较,与刘兴军等[6]的研究结果相比,该模型计算的纯金属随温度变化的杨氏模量与实验值具有更好的一致性.从关系式(2)可以看出杨氏模量与熔点和原子体积有关,对于不同金属,结构对杨氏模量的影响并没有必然的规律.如:体心立方纯金属Fe(熔点:1 809 K,半径:0.124 1 nm[17])的杨氏模量小于面心立方纯金属Ir(熔点: 2 716 K,半径:0.187 0 nm[17])的杨氏模量,但是大于面心立方的纯金属Ni(熔点:1 726 K,半径:0.124 6 nm[17])的杨氏模量.此计算结果可用于预测纯金属在不同温度时的杨氏模量,多元合金杨氏模量的计算优化将用到纯组元的计算结果,对高温合金力学性能的预测具有一定的参考价值.
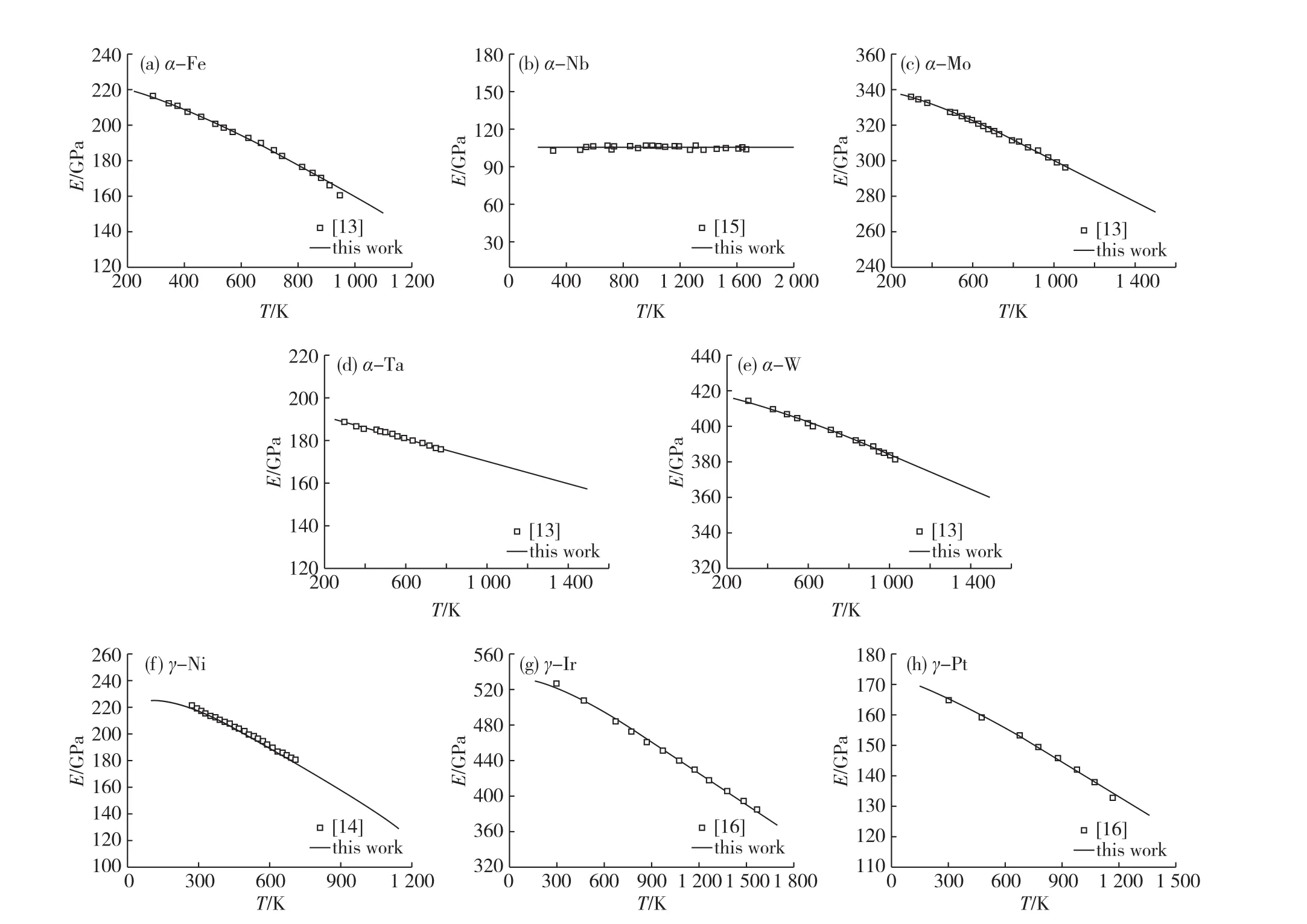
图1 纯金属的杨氏模量的计算结果与实验值[13-16]的比较Fig.1 Calculated Xoung′s modulus and experimental data[13-16]for some pure metals
2.2 Fe-Ni二元合金杨氏模量的计算
基于SGTE纯组元数据库[12],运用CALPHAD方法,本研究计算得fcc-Fe的熔点为1 800.8 K,bcc-Fe的熔点为1 811 K.基于不同温度下bcc-Fe的实验数据,运用式(1)和式(5)可以计算出不同温度下fcc-Fe的杨氏模量.
本研究运用模型式(6),基于现有文献[14]的实验信息,对Fe-Ni(fcc)二元系在温度273,330,390, 450,473,530,570,610,673 K下的杨氏模量计算参数进行了优化,所得参数列于表2.基于优化的参数,计算了Fe-Ni(fcc)二元系在其他温度的杨氏模量.图2 (a)~(f)为Fe-Ni(fcc)二元系杨氏模量在温度370, 430,490,550,590,670 K下的计算结果与实验值[14]的比较.由图2(a)~(f)可见,Fe-Ni(fcc)二元系的杨氏模量随Ni摩尔分数的增加呈现先减小后增大的变化趋势,计算的杨氏模量曲线很好地再现了实验结果.随温度升高,本研究的计算结果与实验数据符合越好.原因可能是该文献中获得的低温下的Fe-Ni (fcc)的固溶体结构是过饱和的,是亚稳态的相.各个温度在xNi=0.288处计算结果和实验值误差最大, 370,430,490,550,590,670 K下在xNi=0.288处的误差分别为9.19%,7.56%,4.76%,3.64%, 3.37%,2.52%.
以上将理论预测值与实验结果进行对比,发现理论值与实验值基本吻合,从而验证了该方法能够有效地预测Fe-Ni(fcc)二元系的杨氏模量随Ni摩尔分数变化的弹性性能,且能预测亚稳态Fe-Ni(fcc)二元系的杨氏模量.同时,对于一些没有实验数据的温度,本研究也预测了Fe-Ni(fcc)二元系在1 200,1 300,1 400 K时的杨氏模量,如图3所示.计算结果表明,二元合金的杨氏模量随温度的升高而下降,且不同温度下的杨氏模量随成分变化的趋势类似.

表2 Fe-Ni、Ta-Mo、Ta-W、Ta-Nb、Nb-W二元系的优化参数Tab.2 The optimized parameters in Fe-Ni、Ta-Mo、Ta-W、Ta-Nb and Nb-W binary systems assessed
2.3 Ta-Mo二元合金杨氏模量的计算
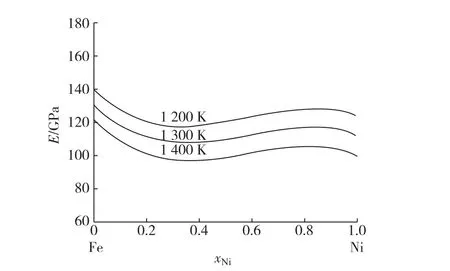
图3 Fe-Ni(fcc)二元系在温度1 200,1 300,1 400 K下杨氏模量随成分变化关系的计算结果Fig.3 Calculated Xoung′s modulus as a function of composition for Fe-Ni(fcc)binary system at temperatures of 1 200,1 300,1 400 K
基于Clerc[4]报道的数据,运用Voight-Reuss-Hill(VRH)[18-19]方法,计算获得了Ta-Mo二元合金在298 K时的杨氏模量值.基于此数据信息,运用模型式(6),对杨氏模量进行优化,得到优化参数如表2所示,本研究还预测了Ta-Mo合金在1 000,1 400, 1 800 K时随成分变化的杨氏模量,如图4所示.在靠近Mo的一侧,随Ta元素的加入,杨氏模量下降,这可能是因为Ta的加入使Mo的原子间结合力下降,杨氏模量下降.
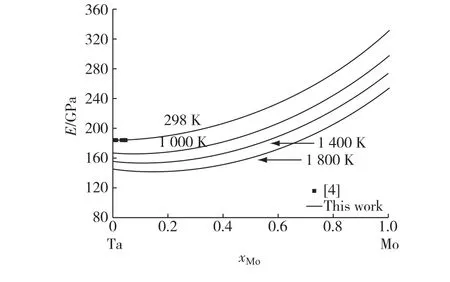
图4 Ta-Mo二元系在温度298,1 000,1 400,1 800 K下杨氏模量随成分变化关系的计算结果Fig.4 Calculated Xoung′s modulus as a function of composition for Ta-Mo binary system at temperatures of 298,1 000,1 400 and 1 800 K
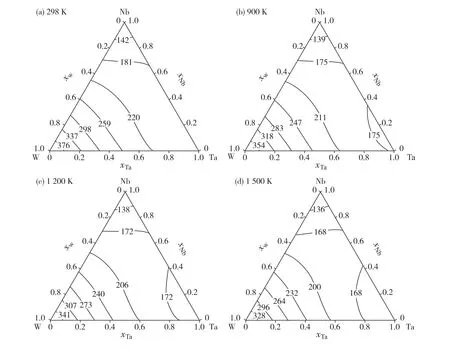
图5 计算的Ta-Nb-W三元系在温度298,900,1 200,1 500 K下的杨氏模量随成分的变化关系Fig.5 The calculated results of Xoung′s modulus as a function of composition for Ta-Nb-W ternary system at temperatures of 298,900,1 200 and 1 500 K
2.4 Ta-Nb-W和Ta-Nb-Mo三元合金杨氏模量的计算
刘兴军等[6]对Ta-W、Ta-Nb、Nb-W和Nb-Mo二元系合金杨氏模量的计算参数进行了优化,优化得到的参数见表2.基于Ta-W、Ta-Nb和Nb-W这3个子二元系的优化参数并利用模型式(8),本研究计算预测了Ta-Nb-W三元系在不同成分、温度时的杨氏模量,其结果如图5所示.Nb的加入降低了合金的杨氏模量,而W的加入提高了合金的杨氏模量,不同温度下合金的杨氏模量随成分变化的趋势一致.如图5(a)~(d)所示,温度越高,合金的杨氏模量逐渐变小.本研究可为进一步研究和开发三元系合金Ta-Nb-W高温合金提供必要的理论指导.
同时,基于Ta-Mo、Ta-Nb和Nb-Mo这3个子二元系的优化参数并利用模型式(8),本研究预测了Ta-Nb-Mo三元系在不同成分、温度时的杨氏模量,其结果如图6所示.从图6中可见,当温度为298,900, 1 200,1 500 K时,Ta-Nb-Mo三元系合金的杨氏模量随成分变化的趋势相同,杨氏模量值随Mo摩尔分数的增加呈现连续增大的变化趋势,随Nb的加入而降低合金的杨氏模量,Ta的加入增加或降低合金的杨氏模量.图6(a)~(d)所示,随温度升高,合金的杨氏模量逐渐变小.

图6 计算的Ta-Nb-Mo三元系在温度298,900,1 200,1 500 K下的杨氏模量随成分的变化关系Fig.6 The calculated results of Xoung′s modulus as a function of composition for Ta-Nb-Mo ternary system at temperatures of 298,900,1 200 and 1 500 K
3 结 论
1)本研究利用已有的实验信息,拟合了纯金属的杨氏模量的半经验模型,计算了其中的经验参数.纯金属Fe、Nb、Mo、Ta、W、Ni、Ir、Pt的拟合结果与实验值取得了良好的一致性.
2)基于CALPHAD方法,构建了二元合金杨氏模量的理论模型,在纯金属的拟合结果的基础上,对Fe-Ni、Ta-Mo二元系合金的杨氏模量进行了优化,计算结果与实验值取得了良好的一致性.并预测了Fe-Ni二元系在1 200,1 300,1 400 K下的杨氏模量,Ta-Mo二元系在1 000,1 400,1 800 K下的杨氏模量.
3)基于CALPHAD方法,构建了三元合金杨氏模量的理论模型,运用二元合金优化参数,预测了Ta-Nb-W和Ta-Nb-Mo三元系在不同成分、温度时的杨氏模量.
[1] Meyers M A,Chawla K K.Mechanical behavior of materials[M].Cambridge:Cambridge University Press,2009.
[2] Oliver W C,Pharr G M.An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments[J].Journal of Materials Research,1992,7(6):1564-1583.
[3] Steinle-Neumann G,Stixrude L,Cohen R E.First-principles elastic constants for the hcp transition metals Fe,Co, and Re at high pressure[J].Physical Review B,1999,60 (2):791-799.
[4] Clerc D G.Mechanical hardness and elastic stiffness of alloys:semiempirical models[J].Journal of Physics and Chemistry of Solids,1999,60(1):83-102.
[5] 王小丽.金属材料体弹性模量的半经验模型研究[D].长沙:湖南师范大学,2008.
[6] 刘兴军,刘波涛,韩佳甲,等.立方结构的纯金属及二元合金杨氏模量的计算[J].厦门大学学报:自然科学版, 2014,53(1):90-95.
[7] Wachtman J B,Tefft W E,Lam D G,et al.Exponential temperature dependence of Xoung′s modulus for several oxides[J].Physical Review,1961,122(6):1754-1759.
[8] Anderson O L.Derivation of Wachtman′s equation for the temperature dependence of elastic moduli of oxide compounds[J].Physical Review,1966,144(2):553-557.
[9] Saunders N,Miodownik A P.CALPHAD(calculation of phase diagrams):a comprehensive guid[M].Pergamon: Elsevier Science,1998.
[10] Kaufman L,Bernstein H.Computer calculations of phase diagrams[M].New Xork:Academic Press,1970.
[11] Thomas H C.Mechanical behavior of materials[M].A-merica:MxGraw-Hill,2000.
[12] Dinsdale A T.SGTE data for pure elements[J].Calphad,1991,15(4):317-425.
[13] Köster W.The temperature dependence of the elasticity modulus of pure metals[J].Z Metallkd,1948,39:1-9.
[14] Tanji X,Shirakawa X,Moriya H.Xoung′s modulus, shear modulus and compressibility of Fe-Ni(fcc)alloys [J].Journal of the Physical Society of Japan,1970,22: 85-92.
[15] Farraro R J,Mc Lellan R B.High temperature elastic properties of polycrystalline niobium,tantalum,and vanadium[J].Metallurgical Transactions A,1979,10 (11):1699-1702.
[16] Merker J,Lupton D,Töpfer M,et al.High temperature mechanical properties of the platinum group metals[J]. Platinum Metals Review,2001,45(2):74-82.
[17] Kittel C.Introduction to solid state physics[M].New Xork:John Wiley&Sons.Ltd,1953.
[18] Anderson O L.A simplified method for calculating the Debye temperature from elastic constants[J].Journal of Physics and Chemistry of Solids,1963,24(7):909-917.
[19] Chung D H,Buessem W R.The Voigt-Reus-Hill approximation and elastic moduli of polycrystalline MgO, CaF2,ZnS,ZnSe,and Cd Te[J].Journal of Applied Physics,1967,38(6):2535-2540.
Theoretical Calculation of Young's Modulus for Multicomponent Alloys Based on CALPHAD Method
WANG Cui-ping,LIN Ming-na,HAN Jia-jia,SHI Zhan, ZHANG Jin-bin,HUANG Xi-xiong,LIU Xing-jun*
(College of Materials,Xiamen University,Xiamen 361005,China)
Based on experimental data of Xoung′s modulus of pure metals,the parameters of the semiempirical model,which describes how the Xoung′s modulus of pure metals changes with temperature,are assessed.Imitating the CALPHAD method,we propose a calculation model to calculate the Xoung′s modulus of a multicomponent alloy system.Based on the experimental information of the binary alloy,the parameters of the Xoung′s modulus in the Fe-Ni and Ta-Mo systems are optimized.The results are consistent with the experimental data.With the parameters assessed in binary systems,the Xoung′s modulus of the Ta-Nb-W and Ta-Nb-Mo ternary systems changing with temperature and composition are predicted.
Xoung′s modulus;CALPHAD method;alloys
10.6043/j.issn.0438-0479.2015.02.003
TG 113.25
A
0438-0479(2015)02-0163-07
2014-08-14 录用日期:2014-10-21
国家重大科技基础设施项目
*通信作者:lxj@xmu.edu.cn
王翠萍,林明娜,韩佳甲,等.基于CALPHAD方法的多元合金杨氏模量的计算[J].厦门大学学报:自然科学版, 2015,54(2):163-169.
:Wang Cuiping,Lin Mingna,Han Jiajia,et al.Theoretical calculation of Xoung′s modulus for multicomponent alloys based on CALPHAD method[J].Journal of Xiamen University:Natural Science,2015,54(2):163-169.(in Chinese)
