一种优化系数的混合域叠前深度偏移方法

罗仁泽,何国林,黄元溢

(1.油气藏地质及开发工程国家重点实验室,四川成都610500;2.西南石油大学地球科学与技术学院,四川成都610500;3.中国石油集团东方地球物理勘探有限责任公司,河北涿州072751)

一种优化系数的混合域叠前深度偏移方法

罗仁泽1,2,何国林1,2,黄元溢3

(1.油气藏地质及开发工程国家重点实验室,四川成都610500;2.西南石油大学地球科学与技术学院,四川成都610500;3.中国石油集团东方地球物理勘探有限责任公司,河北涿州072751)

为提高偏移中频散方程单平方根算子渐近式的逼近程度,提出了优化系数的混合域叠前深度偏移方法。该方法对频散方程的单平方根算子采用了有理切比雪夫逼近；与连分式展开的逼近算法对比后发现，该优化算法能降低偏移逼近算子与频散方程的单平方根算子的相对误差,从而提高了在陡倾构造及强横向速度变化地区偏移成像的精度。二维SEG/EAGE盐丘模型的偏移成像结果证明：在陡倾角构造及横向速度变化剧烈的地区,优化系数的混合域叠前深度偏移方法比常规的傅里叶有限差分(FFD)法的成像效果更好。

叠前深度偏移;混合域;优化系数;有理式;强横向速度变化

目前,地震勘探的目标逐步转向山地复杂高陡构造区,而山地复杂构造区地震偏移成像精度亟需提高。在现有偏移成像技术中,叠前深度偏移成像技术是山地复杂高陡构造区及强横向速度变化介质精确成像最有效的方法[1-2]。

波动方程叠前深度偏移成像是通过计算波场外推算子实现的[3],波场外推算子的计算精度直接关系到偏移剖面的成像精度。常规计算波场外推算子的方法有：基于射线理论的Kirchhoff积分法[4]、相移(PS)法[5]、Stolt法[6]、相移加插值(PSPI)法[7]、频率-空间域有限差分(FD)法[8-11]、分步傅里叶(SSF)法[12]、傅里叶有限差分(FFD)法[13]及广义屏(GSP)法[14-19]。

近几年,在常规波场延拓算子计算方法的基础上,国内外学者对波场延拓算子做了进一步的研究。Ristow[20]提出利用有理函数展开式对频散方程进行系数的局部优化,该方法具有较高的成像精度,但在每次深度延拓步长内都要计算相应的优化系数,计算效率低。雷秀丽等[21]提出了复padé近似逼近差分算子的叠前深度偏移方法,该算法降低了偏移过程中噪声对偏移剖面成像的影响,能对起伏地表条件下地质体精确成像,但不能对地下复杂高陡构造精确成像。郭恺等[22]提出了算子优化的傅里叶有限差分叠前深度偏移方法,该偏移方法提高了对简单构造的成像效果,但不适用于复杂构造区偏移成像。刘定进等[23]研究了高精度屏算子的偏移成像方法,该方法对宽角度信息成像效果更好,但存在计算效率的问题,偏移算子逼近阶数越高,计算效率越低。杨庆道等[24]提出利用克希霍夫偏移/反偏移得到的数据作为映射算子来提高地震数据信噪比的方法,该方法能够很好地消除偏移过程中产生的随机噪声,提高了偏移剖面的成像精度,但该方法基于水平层状介质偏移成像,对复杂构造区偏移成像效果没有验证。周伟等[25]利用切比雪夫多项式对单平方根算子进行展开,利用模拟退火法对展开的算子进行系数优化,优化的算子对高陡构造精确成像的构造倾角角度能达到60°,但对更高角度的高陡构造不能精确成像。

以上对单程波平方根算子改进的方法,在应用单程波方法时,其上、下行波的波场必须是解耦的,这就要求在单个深度延拓步长之内,介质在纵向上必须均匀(在横向上可以不均匀),这一点在实际的沉积地层中往往能得到满足[26-28],但在复杂的非沉积地层中一般得不到满足。

为解决复杂高陡构造区偏移剖面成像精度不高的问题,本文提出采用有理切比雪夫多项式优化逼近偏移算子的算法,对混合域偏移算子的渐近式系数进行优化,从而减少其与精确频散方程单平方根算子的误差,提高混合域优化系数叠前深度偏移方法在复杂构造区及强横向速度变化介质的成像精度。

1 一种新的优化系数的混合域叠前深度偏移方法

二维波动方程为：

(1)

式中：v=v(x,z)为介质速度(m/s);(x,z)为二维坐标;u=u(x,z;t)为地震波场值;t为时间(s)。

对上述二维波动方程进行傅里叶变换到频率-空间域,则下行波单程波方程为：

(2)

基于速度场分裂思想,将整个速度分裂为常速背景和变速扰动,设背景速度为v0(x,z),用v0(x,z)代替介质速度v(x,z),则(2)式可化为：

(3)

对比(2)式和(3)式,则(2)式中的单平方根算子A的误差E为：

(4)

采用傅里叶变换,将(4)式变换到频率-波数域,有：

(5)

式中：kx为x方向上的波数。

(6)

假设(6)式的最佳逼近式为：

(7)

将(7)式代入(5)式,则有：

(8)

将(8)式变换到频率-空间域,并代入(3)式得：

(9)

则偏移延拓算子A可表示为：

(10)

下行波的外推过程可表示为：

(11)

式中：A1表示f-k域相移法的偏移延拓算子;A2表示f-x域的时移校正算子;A3表示f-x域扰动项波场有限差分算子。

现有计算混合域叠前深度偏移波场延拓算子的方法为连分式展开。有理切比雪夫逼近算子比常用的连分式展开逼近算子的误差更小,逼近精度更高。我们采用有理切比雪夫多项式[29]对所求的偏移算子系数进行优化,并分析优化系数后的偏移算子误差,进而调整系数,使优化系数后的偏移算子能够更精确地逼近偏移算子的精确值,从而提高偏移成像的精度。

2 优化系数的混合域叠前深度偏移性能分析

为了检验优化系数的混合域叠前深度偏移的性能,将优化系数的混合域叠前深度偏移算子与连分式展开求取的系数的混合域叠前深度偏移算子进行对比。

2.1 有理切比雪夫逼近

有理切比雪夫算法的原理是对一个函数f(x)展开成切比雪夫多项式[30]：

(12)

式中：N为展开式的阶数;Ck为切比雪夫系数;Tk(x)为切比雪夫多项式。Ck与Tk(x)满足以下的关系式：

T0(x)=1

T1(x)=x

(13)

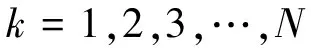
(14)

假设用如下的n次有理函数P(x)逼近函数f(x),则

(15)

式中：n=N/2为p,q项的阶次,且q0=1。

在区间[-1,1]的函数f(x)与P(x)的差值为：

(16)

为使函数f(x)高度逼近函数P(x),选择系数q0,q1,…,qn和p0,p1,…,pn使(16)式等号右边对于Tk(x)(k=1,2,…,N)为0。

利用切比雪夫多项式Ti(x)的性质,则可得到系数关系式为:

(17)

(18)

(19)

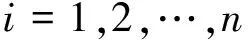
2.2 有理切比雪夫逼近优化系数

利用有理切比雪夫逼近算法对(7)式进行逼近,求得的混合域叠前深度偏移算子的优化系数为：a=0.4557和b=0.3996,则(7)式可转化为：

(20)

(7)式的连分式表达为：

(21)

设波的入射角为θ,由波数定义可得：

(22)

则(20)式与偏移延拓算子精确值的相对误差为：

(23)

(21)式与偏移延拓算子精确值的相对误差为：

(24)

图1为(23)式、(24)式的相对误差Er(θ)随入射角θ变化的误差曲线。

对比图1中两条相对误差曲线,可以看出：在角度小于51°时,本文优化后的延拓算子与连分式展开的延拓算子的相对误差基本相同;但在角度大于51°时,随着构造倾角的增大,本文优化后的延拓算子相对误差比连分式展开的延拓算子的相对误差更小,这说明本文提出的优化系数的混合域叠前深度偏移算子在构造陡倾角处能更好地逼近单平方根算子的精确值。

为了进一步验证本文提出的优化系数的混合域叠前深度偏移算子逼近精确算子的效果,通过计算上述两种方法的相对误差绝对值的数学期望值E进行验证,即：

(25)

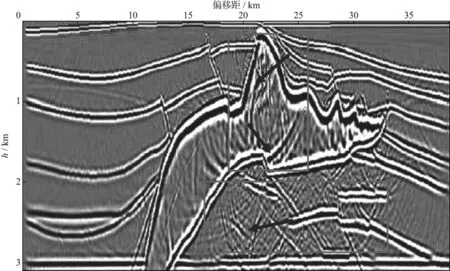
通过数值计算,本文提出的优化系数混合域叠前深度偏移算子和常规连分式展开的混合域叠前深度偏移算子与精确叠前深度偏移算子相对误差的数学期望值分别为：E优=0.170000,E连=0.314285。由于E优

图1 优化系数、连分式展开的单平方根算子与精确单平方根算子的相对误差曲线

3 基于优化系数的混合域叠前深度偏移算子模拟成像

为了检验本文提出的优化系数的混合域叠前深度偏移方法的成像效果,采用本文提出的优化系数的混合域叠前深度偏移方法和基于连分式展开的混合域叠前深度偏移算子的偏移算法分别对二维SEG/EAGE盐丘模型进行叠前深度偏移成像。对比这两种算法所获得的偏移成像剖面,以检验本文算法的成像效果。

二维SEG/EAGE盐丘模型(图2)具有复杂的地质特征,构造复杂及横向速度变化剧烈,尤其是中间高速部分的盐丘,往往是成像的难点。该模型的速度场参数为：横向采样点1290个,纵向采样点300个,横向采样间隔12m,纵向采样间隔12m。

对二维SEG/EAGE盐丘模型分别采用基于连分式展开的混合域叠前深度偏移算法和优化系数的混合域叠前深度成像算法进行叠前深度偏移成像,结果如图3和图4所示。

对比图3和图4中红框区域成像效果可见,图4 偏移剖面的成像精度得到了大幅度的提高,盐丘模型构造形态、构造边界以及深层构造成像更加清晰,尤其是盐丘模型的陡倾构造形态更加清晰,并且绕射波更收敛。这说明,本文提出的优化系数的混合域叠前深度偏移方法能使地震波振幅得到加强,绕射波得到收敛,对陡倾构造具有更高的成像精度。

图3 二维SEG/EAGE盐丘模型连分式展开的混合域叠前深度偏移剖面

图4 二维SEG/EAGE盐丘模型优化系数的混合域叠前深度偏移剖面

4 结论

采用优化系数的混合域叠前深度偏移方法对二维SEG/EAGE盐丘模型进行偏移成像,验证了采用优化系数的混合域叠前深度偏移的成像效果要优于连分式展开的混合域叠前深度偏移。

由于本文提出的优化系数的混合域叠前深度偏移能更好地逼近精确值,提高了对复杂构造及强横向速度变化介质的描述精度,因此,在陡倾角及横向速度剧烈变化的地区采用本文提出的优化系数的混合域叠前深度偏移能取得更好的成像效果。

[1] Kumar D,Sen M K,Ferguson R J.Travel time calculation and prestack depth migration in tilted transversely isotropic media[J].Geophysics,2004,69(1):37-44

[2] Zhu J M,Mathewson J,Liebelt G.A case study for azimuthally anisotropic prestack depth imaging of an onshore Alaska prospect[J].Geophysics,2010,75(4):177-186

[3] 黄元溢.复杂高陡构造区叠前深度偏移技术研究[D].成都：西南石油大学,2012 Huang Y Y.A study of pre-stack depth migration in complex high steep structural zone[D].Chengdu:Southwest Petroleum University,2012

[4] Keho T,Beydoun W B.Paraxial ray Kirchhoff migration[J].Geophysics,2012,77(12):1540-1546

[5] Gazdag J.Wave equation migration with the phase shift method[J].Geophysics,1978,43(6):1342-1351

[6] Stolt R H.Migration by Fourier transform[J].Geophysics,1978,43(1):23-48

[7] Gazdag J,Sguazzero P.Migration of seismic data by phase shift plus interpolation[J].Geophysics,1984,49(2):124-131

[8] 马在田.高阶方程偏移的分裂算法[J].地球物理学报,1983,26(4):377-388 Ma Z T.Splitting algorithm on higher order wave equation migration[J].Chinese Journal of Geophysics,1983,26(4):377-388

[9] Claerbout J F.Imaging the earth’s interior[M].USA：Blackewell Scientific Publications,1985：217-218

[10] Li Z.Compensating finite-difference errors in 3-D migration and modeling[J].Geophysics,1991,56(10):1650-1660

[11] 程玖兵,王华忠,马在田.双平方根方程三维叠前深度偏移[J].地球物理学报,2003,46(5):676-683 Cheng J B,Wang H Z,Ma Z T.Double square root equation 3D prestack depth migration[J].Chinese Journal of Geophysics,2003,46(5):676-683

[12] Stoffa P L,Fokkema J T,de Luna F R M,et al.Split-step Fourier migration[J].Geophysics,1990,55(4):410-421

[13] Ristow D,Ruhl T.Fourier finite-difference migration[J].Geophysics,1994,59(12):1882-1893

[14] Wu R S,Huang L J.Scattered field calculation in heterogeneous media using the phase-screen propagator[J].Expanded Abstracts of 62ndAnnual Internat SEG Mtg,1992,1289-1292

[15] Huang L J,Wu R S.Prestack depth migration with accoustic screen propagators[J].Expanded Abstracts of 66thAnnual Internat SEG Mtg,1996,415-418

[16] Jin S W,Wu R S.Depth migration with a windowed screen propagator[J].Journal of Seismic Exploration,1999,8(1):27-38

[17] 匡斌,王华忠,陈世军,等.傅里叶有限差分深度偏移成像方法研究和应用[J].石油地球物理勘探,2001,36(6):698-703 Kuang B,Wang H Z,Chen S J,et al.Study and application of Fourier finite-difference depth migration method[J].Oil Geophysical Prospecting,2001,36(6):698-703

[18] 吴如山,金胜汶,谢小碧.广义屏传播算子及其在地震波偏移成像方面的应用[J].石油地球物理勘探,2001,36(6):655-664 Wu R S,Jin S W,Xie X B,et al.Generalized screen propagator and its application in seismic wave migration imaging[J].Oil Geophysical Prospecting,2001,36(6):655-664

[19] 金胜文,许士勇,吴如山.基于波动方程的广义屏叠前深度偏移[J].地球物理学报,2002,45(5):684-690 Jin S W,Xu S Y,Wu R S.Wave equation based prestack depth migration using generalized screen propagator[J].Chinese Jouranl of Geophysics,2002,45(5):684-690

[20] Ristow D,RuHI T.Fourier finite-difference migration[J].Geophysics,1990,55(4):410-421

[21] 雷秀丽,李振春,孔雪,等.起伏地表条件下基于复padé逼近的叠前深度偏移[J].地球物理学进展,2012,27(5)：2100-2106 Lei X L,Li Z C,Kong X,et al.Prestack depth migration using complex Padé approximations for irregular surfaces[J].Progress in Geophysics,2012,27(5)：2100-2106

[22] 郭恺,仝兆岐,李振春,等.基于算子优化的Fourier有限差分法保幅叠前深度偏移[J].中国石油大学学报(自然科学版),2012,36(2):91-96 Guo K,Tong Z Q,Li Z C,et al.True-amplitude prestack depth migration based on operator optimized Fourier finite difference method[J].Journal of China University of Petroleum (Edition of Natural Science),2012,36(2):91-96

[23] 刘定进,周云何,杨瑞娟,等.高精度屏算子地震偏移成像方法研究[J].石油物探,2010,49(6):531-535 Liu D J,Zhou Y H,Yang R J,et al.Seismic migration imaging method by using high-precision screen operators[J].Geophysical Prospecting for Petroleum,2010,49(6):531-535

[24] 杨庆道,蒋兵,岳玉波,等.基于Kirchhoff偏移/反偏移的随机噪声压制方法[J].石油物探,2013,52(5):530-536 Yang Q D,Jiang B,Yue Y B,et al.A random noise suppression method based on data mapping by Kirchhoff migration/demigration[J].Geophysical Prospecting for Petroleum,2013,52(5):530-536

[25] 周伟,张金海,姚振兴.非均匀VTI介质切比雪夫傅里叶深度偏移方法[J].地球物理学进展,2012,27(4):1359-1365 Zhou W,Zhang J H,Yao Z X.Chebyshev Fourier depth migration operator for heterogeneous VTI media[J].Progress in Geophysics,2012,27(4):1359-1365

[26] 刘礼农,崔凤林,张剑锋.三维复杂构造中地震波模拟的单程波方法[J].地球物理学报,2004,47(3):514-520 Liu L N,Cui F L,Zhang J F.Seismic modeling with one-way wave equation in 3D complex structures[J].Chinese Journal of Geophysics,2004,47(3):514-520

[27] 首皓,孙鲁平,刘红伟,等.复杂介质地震波场模拟的单程波方程[J].石油物探,2009,48(5):479-482 Shou H,Sun L P,Liu H W,et al.One-way wave method for seismic wavefield simulation for complex medium[J].Geophysical Prospecting for Petroleum,2009,48(5):479-482

[28] 何兵寿,张会星,魏修成,等.双程声波方程叠前逆时深度偏移的成像条件[J].石油地球物理勘探,2010,45(2):237-243 He B S,Zhang H X,Wei X C,et al.Imaging conditions for two-way acoustic wave equation pre-stack reverse-time depth migration[J].Oil Geophysical Prospecting,2010,45(2):237-243

[29] 李文,白晶.基于有理切比雪夫逼近的分数阶微积分算子的离散化[J].大连交通大学学报,2010,31(4):45-49 Li W,Bai J.Discretization of the fractional order differentiator/integrator based on the rational Chebyshev approximation[J].Journal of Dalian Jiaotong University,2010,31(4):45-49

[30] Burden R L,Faires J D.Numerical analysis[M].Kentucky:Brooks Cole,2005:452-470

(编辑：顾石庆)

A new prestack depth migration method in hybrid domain with optimization coefficient

Luo Renze1,2,He Guolin1,2,Huang Yuanyi3

(1.StateKeyLaboratoryofOilandGasReservoirGeologyandExploitation,Chengdu610500,China; 2.SchoolofGeoscienceandTechnology,SouthwestPetroleumUniversity,Chengdu610500,China; 3.BGP,CNPC,Zhuozhou072751,China)

To improve the approximation degree of single square-root operator of frequency dispersion,prestack depth migration by hybrid domain with optimization coefficient was proposed.This method is designed to calculate the optimization coefficient by rational Chebyshev approximation to approach the single square-root operator of frequency dispersion.By comparison on the rational Chebyshev approximation and continued fraction approximation,it is discovered that the rational Chebyshev approximation can reduce the relative error between optimization coefficient migration operator and single square-root operator of frequency dispersion.Therefore,our method can improve the precision of migration imaging in the area with high-steep structures and strong lateral velocity variation.The application on 2-D SEG/EAGE salt dome model proves the prestack depth migration in hybrid domain with optimization coefficient has better imaging effect than conventional Fourier finite difference (FFD) in the area with high-steep structures and strong lateral velocity variation.

prestack depth migration,hybrid domain,optimization coefficient,rational expression,strong lateral velocity variation

2014-11-16;改回日期：2015-03-18。

罗仁泽(1973—),男,教授,博士生导师,长期从事地震信号采集和处理方法研究工作。

油气藏地质及开发工程国家重点实验室开放基金项目(PLC201104)资助。

P631

A

1000-1441(2015)05-0501-07

10.3969/j.issn.1000-1441.2015.05.003