层析反演中的正则化方法研究

李 辉,王华忠,张 兵,3

(1.同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092;2.青凤致远应用地球物理研究所,上海200093;3.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

层析反演中的正则化方法研究

李 辉1,2,王华忠1,张 兵1,3

(1.同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092;2.青凤致远应用地球物理研究所,上海200093;3.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

正则化可显著降低层析反演解的非唯一性，提高层析反演结果的质量。主要研究了模型参数正则化和数据正则化。地下介质参数之间的关联性如何加入模型正则化是讨论的问题之一；观测数据之间的关联性加入数据正则化的方法则是另一个主要议题。此外，讨论了Tikhonov正则化和预条件两种模型正则化实现策略，指出前者理论比较直观，后者计算效率更高，并证明了两者在理论上的等价性。模型正则化通过构造各向异性光滑算子加入地质构造特征，数据正则化则通过在层析矩阵中加入预先构造的数据预条件矩阵来实现。通过层析偏移速度分析给出了模型正则化和数据正则化的具体实现策略。理论分析和层析偏移速度分析的数值实验说明本文的模型正则化和数据正则化可显著提高层析反演的质量。

层析偏移速度分析；模型正则化；数据正则化；预条件；地质构造约束

随着勘探地震技术的发展以及石油工业需求的提高,叠前深度偏移逐渐成为工业应用中偏移技术的主流。在观测数据品质有保障的前提下,叠前深度偏移在实际应用中成功与否最重要的前提是速度模型的准确程度。深度域速度建模的方法包括分析类方法(如扫描速度分析、剩余曲率分析)、层析方法、波动方程类反演(如全波形反演)方法等。其中,分析类方法存在较强的理论假设,导致估计的速度精度及分辨率非常低;波动方程类反演方法的效率非常低,且严重依赖于初始速度模型;基于射线理论的层析方法是目前工业界应用最广泛的深度域速度估计方法[1-3],但存在明显的缺点,如:只能反演光滑的背景速度、建立的反问题病态性较明显等,所幸的是,正则化可显著解决射线层析中的上述问题[4-5]。尽管正则化的本质思想十分明确,但具体实现方法及种类繁多,本文针对模型参数之间的关联性和数据之间的关联性讨论层析反演中加入正则化的策略。

正则化是地球物理反问题中非常重要的环节,可以显著降低层析反演解的非唯一性,提高层析反演结果的质量。地震层析反演中的模型参数是地下介质参数(通常是地震波速度),数据是观测到的波场信息(通常是旅行时)。地下不同空间区域的介质参数之间有一定关联性;同样,不同观测点的数据也相互关联。此外,测量的地震波数据良莠不齐,可靠性存在明显差异。如何把这些信息加入层析过程以提高反演质量是一个值得研究的课题。

在地震层析反演中,利用地下构造信息约束模型参数的空间分布特征,把模型参数在空间中的相关特征通过构造信息提取出来,结合Tikhonov模型正则化或预条件思想把此信息加入层析反演中,可显著改善估计的模型参数,这里称之为模型正则化。Zhou等[6]、Zhou[7]和Zdraveva等[8]把光滑算子加入灵敏度核函数中对反演的模型直接进行正则化约束;Clapp[9]和Clapp等[10]利用预条件思想实现对反演模型的预条件约束。事实上,Tikhonov模型正则化和预条件模型正则化等价,虽然两者有不同的表达形式及理论基础。类似于模型参数,利用协方差矩阵可提取出观测数据之间的相关性,将数据相关性作为数据先验信息加入反演过程是贝叶斯反演思想[4]的一个关键环节。此外,测量的数据有优劣之分,反演中如何通过正则化突出质量较高的数据也是本文的研究内容。层析中加入数据关联性和突出高质量的数据称为数据正则化。

1 模型正则化理论及实现策略

层析反演中针对模型施加正则化是把我们对模型参数的认识加入层析反演中。地下介质的模型参数化后,不同参数之间存在一定的关联性,因为所有参数组成的地下介质遵循一定的地质规律。这里研究的模型正则化试图在层析过程中加入地质构造约束,我们通过在层析矩阵中加入光滑矩阵来实现。光滑矩阵可约束模型中不同方向的突变成分,令垂直于反射界面与平行于反射界面的方向光滑强度不同来实现对模型的各向异性光滑约束。

模型正则化的具体实现策略包括Tikhonov模型正则化和预条件模型正则化两种。无论是Tikhonov正则化还是预条件模型正则化,光滑矩阵的构建是重要的一环。

1.1 Tikhonov模型正则化

贝叶斯框架下层析反演等价于优化如下的目标泛函[4]:

(1)

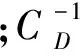
(2)

式中:矩阵A是A(m)的线性化算子;Δm=m-m0是当前迭代中模型的更新量;m0是参考模型;Δd=Am0-d是当前迭代中的数据残差。

目标泛函((1)式)和方程(2)中的协方差矩阵及阻尼因子实现了对层析反演施加正则化。不考虑正则化,仅用数据残差进行层析反演,即协方差矩阵为单位矩阵且ε=0时,层析方程(2)退化成一般的层析方程,即:

(3)

令方程(2)中的数据协方差矩阵为单位矩阵,只考虑模型正则化时的层析方程为:

(4)

模型协方差矩阵的逆矩阵不能直接构造,一般利用其它矩阵代替,从而实现对模型的正则化约束。Xu等[11]和Zhou[7]约束了模型的突变成分,试图得到模型的光滑解,方程(4)可写成:

(5)

式中:R是粗糙化算子,用于提取模型的突变部分。方程(5)即为层析中加入光滑正则化后的方程,其对应的解为光滑解。事实上,方程(5)所表达的模型正则化即为Tikhonov模型正则化[12]。

模型正则化的关键是如何在方程(5)中引入构造信息。提取模型突变部分可对模型向量做微分,典型的方式为拉普拉斯算子作用到模型向量上。已知模型的构造特征时,可令R垂直于地质界面方向，提取Δm的突变信息时,空间展布范围较窄,平行于界面方向时展布范围较宽,从而构造出包含地质构造特征的各向异性粗糙化算子R。等价于约束平行于界面方向较垂直界面方向更加光滑,实现对模型的各向异性光滑约束。此时，方程(5)的解即为引入地质构造信息的模型正则化反演结果。

粗糙化算子R的逆矩阵是一个光滑算子,相对于粗糙化矩阵,光滑矩阵更容易构造,且物理意义更为明确。所以,我们进一步改造方程(5),利用光滑算子对层析问题施加正则化。在方程(5)两端左乘矩阵(RTR)-1,得到:

(6)

即:

SSTATAΔm+εΔm=SSTATΔd

(7)

式中:S是R的逆矩阵,是一个光滑算子。光滑矩阵S中地质构造特征体现为沿构造界面方向的平滑范围较大,垂直构造界面方向的平滑范围较小。

1.2 预条件模型正则化

方程(3)所示的层析问题在模型预条件[11]思想下可表示为:

ASu=Δd

(8)

(9)

式中:S是预条件算子;u为层析方程的预条件解。先求解方程(8),将求解结果u代入公式(9)即可得到最终的解Δm。预条件层析方程(8)的阻尼最小二乘方程为:

STATASu+εu=STATΔd

(10)

方程(10)对应的解是方程(8)的阻尼最小二乘解[13-14]。

下面讨论模型预条件方程((8)式和(9)式)与Tikhonov模型正则化策略((5)式)之间的关系,从而探讨方程(10)中矩阵S与地质构造正则化之间的关系。把预条件方程(9)代入方程(10),预条件层析的阻尼最小二乘方程变成:

STATAΔm+εS-1Δm=STATΔd

(11)

在方程(11)两端左乘矩阵(ST)-1,得到:

(12)

即:

(13)

对比方程(5)和方程(13),当方程(13)中矩阵S为方程(5)中矩阵R的逆矩阵时两方程等价。

由上述分析可知,理论上,预条件层析问题方程(8)和方程(9)的阻尼最小二乘解等价于方程(5)所示Tikhonov模型正则化的解,前提是预条件算子S与正则化算子R互为逆矩阵。与Tikhonov模型正则化相同,当S是光滑算子时,预条件方程(8) 的最小二乘阻尼解u利用(9)式计算出的最终解Δm等价于对层析施加光滑正则化后得到的解。

对比方程(5),方程(7)和方程(8)可知,构建方程(5)需要计算2次矩阵乘,构建方程(7)需计算3次矩阵乘,构造方程(8)仅需1次矩阵乘。从构建层析方程的计算效率上看,方程(8)最优。Clapp等[10]指出方程(8)所示的预条件正则化方式收敛性优于方程(5)所示的模型约束的Tikhonov正则化。

1.3 光滑矩阵的构建策略

如何构建地质构造约束的光滑矩阵是模型正则化的关键点。光滑矩阵的每一行都是地下介质空间中的一个光滑函数[6]。我们令此光滑函数为高斯光滑函数,在不考虑地质构造时,光滑矩阵中第i行第j列的元素为:

(14)

式中:xi,yi,zi是第i行高斯函数中心点空间坐标的3个分量,xj,yj,zj是第j列对应的空间位置的3个坐标分量,σx,σy,σz是高斯函数在3个坐标方向的标准差。将地质构造特征加入光滑矩阵中,(14)式表达的高斯函数在三维空间平移加旋转至一个局部笛卡尔坐标系中,该局部坐标系的坐标方向标记为u,v,w,其中u与地质界面的走向一致,w坐标轴与地质界面垂直,u,v,w组成一个右手系,称此坐标系为“局部地质坐标系”。在此局部坐标系中,定义光滑矩阵中的高斯函数为:

(15)

式中:σu i,σv i,σw i是高斯函数在局部坐标系中的标准差。在实际应用中,σu i和σv i比σw i大,即在平行于地质界面方向的光滑范围较大,垂直于地质界面方向的光滑范围小。这样,层析反演模型参数的空间分布特征被已知的地质特征约束。

局部地质坐标系由原始笛卡尔坐标系的平移和旋转得到。原始坐标系的原点位于(0,0,0)T,局部地质坐标系的原点在原始坐标系中位于(xi,yi,zi)T,所以坐标变换中的平移量等于(xi,yi,zi)T。平移后的坐标系通过三维旋转可得局部地质坐标系。如图1所示,首先把坐标系以z坐标轴为中心旋转角度φ,x坐标轴旋转至与地质走向一致,此时x,y坐标分别写成x′,y′;然后以x′坐标轴为中心旋转角度θ,z坐标轴旋转至垂直于地质界面的方向。旋转后的坐标系即为局部地质坐标系。旋转角度的定义为面对中心坐标轴观察时沿逆时针方向旋转的角度,如图1所示。以z轴与x轴为中心旋转的旋转矩阵分别为:

(16)

(17)

局部地质坐标系中的坐标(u,v,w)T与原始坐标系中坐标(x,y,z)T的关系为:

(18)

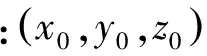
图1 三维坐标旋转示意图解

从上述过程可知,构建含构造特征的光滑矩阵时需要地质构造的倾角信息以及高斯光滑函数的标准差σu i,σv i,σw i。数值实验部分将结合具体数据给出倾角信息和标准差的提取过程。

2 数据正则化理论及实现策略

层析反演中针对数据施加正则化是把我们对数据的认识加入层析反演中。层析反演中正则化关注的数据特点主要有两种:①类似于不同模型参数间的关系,不同数据之间也存在一定的关联性,例如单炮数据中同一波前的信号特征(如旅行时、振幅、相位)在不同检波点的变化应连续;②不同观测数据在测量过程中有不同的准确性,即不同数据的可信程度不同,例如层析反演中检测波前到达时,不同数据的检测精度不同。如何在层析过程中考虑数据的特点是数据正则化的主要任务。我们在基于角度域共成像点道集的层析偏移速度分析中考虑数据正则化问题。

数据之间的关联性同样可以通过对数据进行光滑加入层析反演中。此时需对相关联的数据平滑,消除它们之间由人为因素引入的突变。层析方程(3)在考虑数据关联性后可表达为:

AΔm=CΔd

(19)

其中,矩阵C对数据向量Δd改造,使得相关联的数据之间变化平缓,符合物理规律。层析偏移速度分析在成像域(偏移剖面和共成像点道集)测量数据,实现反射波旅行时层析,具体实现方法不再赘述,可参考文献[1]和文献[15]。层析偏移速度分析中考虑数据关联性主要包括两方面:①反射点邻近、反射角相同的射线对应的数据残差不应存在突变(图2a);②同一反射点反射角邻近的反射射线对应的数据残差不应存在突变(图2b)。矩阵C修改满足上述两个条件的数据,使数据间满足上述物理规律。

图2 存在关联性的反射射线

不同于其它层析方法,层析偏移速度分析中的数据测量过程比较复杂[15],首先在偏移剖面中扫描反射面倾角,同时在成像道集中拾取不同反射角度的反射点成像深度,最后把不同角度之间的成像深度差转换成反射射线的旅行时残差。复杂的数据测量过程可能导致测量数据的误差较大,例如反射面倾角误差、不同反射角成像深度误差等都将转移至最终的数据误差中,所以,在层析偏移速度分析中考虑测量数据的准确性尤为重要。我们对此问题的解决方案是压制精度较低数据同时提升精度较高数据在层析反演过程中所起的作用,具体策略是在层析方程(3)中加入权系数矩阵,即:

WAΔm=WΔd

(20)

图3 偏移剖面中的倾角与相似系数示意

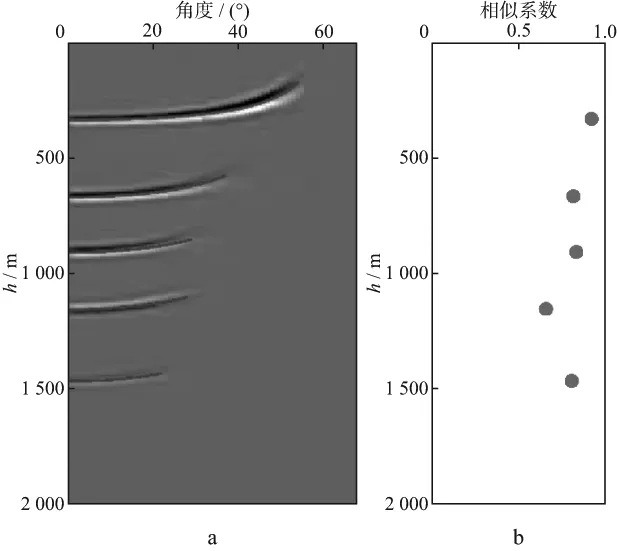
图4 角度域共成像点道集中的拾取曲线与相似系数示意

式中:W是对角矩阵,其对角元素是数据对应的权系数,数据精度越高系数越大,数据精度越低系数越小。关于数据质量的正则化的关键点是如何考察不同数据的测量精度。层析偏移速度分析中数据测量精度取决于在偏移剖面上扫描反射面倾角和在共成像点道集中拾取成像深度的精度,所以只需考察反射面倾角和成像深度的精度即可。反射面倾角准确时,偏移剖面上反射同相轴沿倾角方向连续性较好,否则同相轴不连续。如图3所示,在偏移剖面中通过沿倾角方向信号的相似系数考察所测倾角的精度,其中红色实线是正确反射面倾角方向,虚线是不正确的倾角参考方向,倾角方向准确时计算的相似系数接近1,其它方向的相似系数相对非常小。图3中定义竖直向上方向的角度为0,逆时针方向旋转为正角度。同样,在共成像点道集中拾取不同角度成像深度的精度也用相似系数考察。图4a显示了在角度域共成像点道集中自动拾取的成像深度,图4b是不同层位拾取结果的相似系数对比,图中5个红色圆点是图4a中5个同相轴拾取位置的相似系数,可见,拾取质量比较好的同相轴对应的相似系数接近1,拾取质量较差的同相轴对应的相似系数较小。最终,方程(20)中矩阵W中的权系数可通过上述两种相似系数来确定:

(21)

综合模型正则化和数据正则化,可得最终的层析方程。

Tikhonov模型正则化策略((7)式)结合数据正则化策略((19)式和(20)式)可得层析方程为:

SSTATWTWAΔm+εΔm=SSTATWTCΔd

(22)

模型预条件正则化策略((8)式和(9)式)结合数据正则化策略((19)式与(20)式)可得层析方程为:

WASu=WCΔd

(23)

Δm=Su

(24)

上文分析了层析问题关于模型正则化与数据正则化的理论方法。模型正则化包括Tikhonov模型正则化和预条件模型正则化,前者理论直观,后者计算效率较高。理论分析结果表明,Tikhonov模型正则化和预条件模型正则化在理论上等价。数据正则化考虑了数据参数之间的关联性以及不同的数据质量。结合模型正则化和数据正则化,可得最终的正则化方程。

3 数值实验

本文理论部分地质构造约束的模型正则化与数据正则化可应用在不同种类的层析成像中,例如初至波层析、井间层析、倾斜层析以及层析偏移速度分析等。层析偏移速度分析[1,16]是一种经典的深度域速度建模方法,其缺点是射线角度覆盖范围较小,所以相应的层析问题病态性严重。这里将地质约束的正则化策略应用于层析偏移速度分析,以提高层析的稳定性,同时改善反演的质量。相对于偏移距域共成像点道集(ODCIG),角度域共成像点道集(ADCIG)更加符合物理规律,并且在ADCIG中实现层析偏移速度分析时层析核函数的构建只需进行初值射线追踪,而ODCIG中的层析偏移速度分析构建核函数时必须做耗时且不稳定的两点射线追踪,所以,本文在角度域共成像点道集中实现层析偏移速度分析。

层析偏移速度分析的实现流程如图5所示。基于已知的初始速度模型进行叠前深度偏移并生成ADCIG,以道集中同相轴是否拉平为准则考察速度场的优劣。ADCIG中同相轴不平时在偏移剖面中选取反射点用于反射层析,并计算反射点处的构造倾角,在ADCIG中拾取不同角度的成像深度,同时把不同角度的成像深度转化为旅行时差,即为层析反演中的数据残差。根据反射点的地下位置、反射角度和偏移剖面中的界面倾角,利用初值射线追踪模拟出反射射线,建立无约束的层析矩阵,即层析方程(3)中的矩阵A。同时,利用偏移剖面和ADCIG建立正则化矩阵方程。求解层析方程更新初始速度,得到更新后的速度场。如此,则实现了层析偏移速度分析的一次迭代。

图5 层析偏移速度分析流程

上文讨论了两种构造约束的模型正则化策略,这里,通过预条件正则化测试本文地质构造约束的正则化方法。此外,我们也对两种数据正则化方式进行测试,以考察数据正则化对层析的影响。

利用二维理论模型和实际数据的二维测线对本文正则化方法进行测试。其中,理论模型测试分为两部分:①模型正则化测试,详细表述模型正则化中构造约束的光滑矩阵如何构建;②数据正则化测试,给出数据正则化影响层析结果的直观认识。

3.1 理论模型测试

理论模型参数及观测系统如表1所示。理论模型(图6a)中有4个沉积层,其中第3层内有一个高速体，其偏移结果如图6b所示。初始速度模型和相应的偏移结果如图7 所示。从偏移结果中提取地质构造倾角和高斯光滑函数的标准差是构建光滑矩阵的关键点。下面将从初始速度偏移剖面出发获取地质构造倾角和高斯函数标准差。模型的构造信息可从图7b所示的偏移剖面中提取,具体策略与偏移速度分析中的反射点倾角提取策略[15]相同,从图7a中得到的反射界面倾角如图8所示,其中无构造区域的倾角置为0。利用偏移剖面和反射界面倾角计算出高斯光滑函数在不同空间点的标准差σu和σw,计算公式为:

(25)

(26)

式中:s是偏移剖面上沿构造方向的相似系数;sthresh是相似系数门槛值,满足s

表1 理论模型参数与观测系统参数

图6 理论速度模型及相应偏移结果

图7 初始速度模型及相应偏移结果

为测试数据正则化对层析结果的影响,人为修改层析偏移速度分析中的数据使之污染,引入部分错误数据。针对此被污染的数据,分别利用无数据正则化(图12)的层析方法和加入数据正则化(图13) 的层析方法更新图7a所示的初始速度模型,更新后的速度模型分别如图12a和图13a所示。对比图12a和图13a 可以看出,圆圈区域由于数据问题,无数据正则化的层析速度明显偏大,加入数据正则化后的层析速度偏小;但就速度更新的特点来看,两者的速度更新方向均正确,前者速度更新量过大,后者速度更新量偏小。前者影响层析的收敛性,可能导致反演结果不收敛;后者影响层析的收敛速度,导致反演收敛慢。从上述分析可知数据正则化的作用是以牺牲收敛效率为代价保证正确收敛。相应的偏移剖面如图12b和13b所示,ADCIG如图12c,图12d,图13c和图13d所示。

图8 初始速度偏移剖面中提取的界面倾角

图9 不同空间位置的标准差

图10 构造约束的反演速度模型及相应的偏移结果

图11 无构造约束反演的速度模型

3.2 实际数据测试

用于测试高斯束层析的数据来源于中国某探区的一条二维测线。该测线共232炮,每炮最大偏移距3200m,最小偏移距100m,左侧单边接收。道间距50m,炮间距大部分为100m,小部分为50m。模型共952个CDP点,CDP间隔25m,深度采样点数为501,深度采样间隔为10m。初始速度模型通过速度分析获得。初始速度模型和相应偏移剖面如图14a和图14b所示。在横向位置为2500,15000,22500m的3个CDP点抽取出3个角度域成像道集如图15a,图15b和图15c所示。从成像道集中可以看出,x=2500m附近初始速度比较准确,同相轴基本水平;x=15000m附近同相轴有微小的下拉现象,速度略微偏大;x=22500m附近的同相轴下拉更加明显,速度偏大。在此初始速度模型的基础上,利用本文模型正则化和数据正则化约束的角度域层析偏移速度分析经过两次迭代得到的速度模型如图16a所示,其中的构造特征不是很明显,这是因为初始速度模型比较接近真实速度的低波数成分,从而速度更新量比较小。图16b是层析反演的速度模型与初始速度模型之差,从图16b中可以看出,速度模型的更新量体现了地下介质的地质构造特征。利用图16a 中的反演速度模型偏移出的成像剖面如图16c所示,从图16c中可以看出,模型中部小断块区域成像更清楚,同时右侧的反射同相轴更加连续,相对于原始剖面成像效果有明显改善。相应的成像道集如图17a,图17b和图17c所示,相比于图15a,图15b和图15c可以看出,原始成像道集中同相轴的下拉现象已经被完全校正,成像效果更好。

图12 无数据约束的反演速度模型及相应的偏移结果

图13 数据约束的反演速度模型及相应的偏移结果

图14 初始速度模型及相应的成像剖面

图15 初始速度模型偏移出的ADCIG

图16 反演结果及相应的成像剖面

图17 反演速度模型偏移出的ADCIG

4 结论与讨论

正则化是层析反演技术的主要发展方向之一,本文讨论了关于模型和数据的正则化方法及其在层析偏移速度分析中的应用。

模型正则化考虑了不同模型参数之间的关联性。我们讨论了模型正则化的两种具体实现方式——Tikhonov模型正则化与预条件模型正则化。Tikhonov模型正则化从贝叶斯反演理论出发,导出在层析过程中利用光滑矩阵实现模型正则化的公式。预条件层析问题的阻尼最小二乘解转化成原模型参数实现了预条件模型正则化。分析了模型正则化的两种实现策略之间的关系,证明了在一定条件下两者的等价性。但预条件正则化的实现效率明显比Tikhonov正则化高。

在上述模型正则化的框架下,把地质构造特征加入层析反演中,其中包含地质构造特征的光滑矩阵是关键点。模型正则化中的光滑矩阵可利用各向异性光滑算子构建,详细讨论了如何构建融合地质构造特征的各向异性光滑算子。

类似于模型参数,不同的观测数据之间也存在关联性。讨论了反射数据之间的两种关联特征——反射点邻近且反射角相同的射线对应的数据之间差别较小,反射点相同且反射角邻近的射线对应的数据之间差别也较小。此外,不同测量数据的测量精度有高低之分,尤其在层析偏移速度分析中由于数据的测量过程比较复杂,人为引入观测误差的可能性更高。

利用一个二维理论模型对模型正则化和数据正则化的具体实现做了详细讨论,主要包括模型正则化中光滑算子的标准差的计算策略,数据正则化中权系数的计算方式。加入正则化后层析反演得到的速度模型表现出了地质构造特征,偏移剖面和成像道集的质量均可与准确速度的偏移结果媲美。二维测线实际数据的应用也得到了满意的速度模型以及相应的偏移结果。

今后的工作方向之一是在精细的偏移结果中提取出反射界面和断层,结合测井数据作为先验信息,将正则化有机地融入层析反演中,以期得到更高波数的速度成分,进一步提高层析速度反演的精度和分辨率。

致谢:感谢中国石油化工集团公司科技部及中国石油化工股份有限公司石油物探技术研究院对WPI研究组及本项研究的支持。

[1] Woodward M J,Nichols D,Zdraveva O,et al.A decade of tomography[J].Geophysics,2008,73(5):VE5-VE11

[2] Hardy P.Ongong R&D in ray based tomography:well worth the effort[J].Expanded Abstracts of 83rdAnnual Internat SEG Mtg,2013,4806-4810

[3] Lambare G,Guillaume P,Montel J P.Recent advances in ray-based tomography[J].Expanded Abstracts of 76thEAGE Annual Conference,2014,We-G103-01

[4] Tarantola A.Inverse problem theory and methods for model parameter estimation[M].Philadelphia:Society for Industrial and Applied Mathematics,2004:1-352

[5] Zhdanov M S.Geophysical inverse theory and regularization problems[M].Amsterdam:Elsevier Science,2002:1-628

[6] Zhou C,Brandsberg-Dahl S,Jiao J.A continuation approach to regularize the reflection tomography with a 3D Gaussian filter[J].Expanded Abstracts of 71stEAGE Annual Conference,2009,U031

[7] Zhou C.Incorporating geologic information into reflection tomography with a dip oriented Gaussian filter[J].Expanded Abstracts of 75thEAGE Annual Conference,2013,Th-04-02

[8] Zdraveva O,Hydal S,Woodward M.Tomography with geological constraint-an alternative solution for resolving of carbonates[J].Expanded Abstracts of 75thEAGE Annual Conference,2013,Th-04-04

[9] Clapp R G.Geologically constrained migration velocity analysis[D].San Francisco:Stanford University,2001

[10] Clapp R G,Biondi B,Claernout J F.Incorporating geologic information into reflection tomography[J].Geophysics,2004,69(2):533-546

[11] Xu S,Zhang Y,Huang T.Enhanced tomography resolution by a fat ray technique[J].Expanded Abstracts of 76thAnnual Internat SEG Mtg, 2006,3354-3358

[12] Tikhonov A N,Arsenin V Y.Solution of ill-posed problems[M].Washington:Winston & Sons,1977:1-258

[13] Backus G E,Gilbert F.The resolving power of gross earth data[J].Geophysical Journal of the Royal Astronomical Society,1968,16(1):169-205

[14] 杨文采.地球物理反演的理论与方法[M].北京:地质出版社,1997:1-271 Yang W C.Theory and methods of geophysical inversion[M].Beijing:Geological Publishing House,1997:1-271

[15] 张兵.基于深度域共成像点道集的层析速度反演与建模方法研究[D].上海:同济大学,2011 Zhang B.The study of tomography and velocity model building based on common imaging gathers[D].Shanghai:Tongji University,2011

[16] Stork C.Reflection tomography in the postmigrated domain[J].Geophysics,1992,57(5):680-692

(编辑：顾石庆)

The study of regularization in tomography

Li Hui1,Wang Huazhong1,Zhang Bing1,2

(1.WavePhenomenaandInversionImagingGroup(WPI),TongjiUniversity,Shanghai200092,China; 2.QingfengzhiyuanAppliedGeophysicsInstitute,Shanghai200093,China;3.SinopecGeophysicalResearchInstitute,Nanjing211103,China)

Regularization in tomography is able to weaken the non-uniqueness of tomography to improve the inversion resultThe discussion of regularization in this paper includes model-regularization and data-regularizationModel parameters are not isolated,how to add the relationship of these parameters into tomography is one of the missions hereSimilarly,considering datum relationship in tomography is another problemThe so-called “straightforward regularization” and the “precondition regularization” are focused,and we achieve that the former is intuitionistic and the latter is more efficiencyAlso,we point out that the above two algorithms are equivalent to each other,and this will be shown in this paperThe geological structure characteristics of the medium can be integrated into the tomography using the model-regularization with anisotropic smooth matrix.The data-regularization is realized with another smooth operator which will be integrated into the tomographic matrix.The model-regularization and data-regularization are tested with tomographic migration velocity analysis (MVA) algorithm.The results of theory and numerical experiments with tomographic MVA show that the proposed model-regularization and the data-regularization are both able to improve the quality of tomography obviously.

tomographic MVA,model-regularization,data-regularization,precondition,geological structure constraint

2014-11-24;改回日期：2015-02-26。

李辉(1985—),男,博士,现从事射线类偏移与反演的研究工作。

国家自然科学基金(41374117)、国家重点基础研究发展计划(973计划)项目(2011CB201002)、国家科技重大专项项目(2011ZX05003-003,2011ZX05005-005-008HZ,2011ZX05006-002)和中国石化地球物理重点实验室开放基金项目(33550006-14-FW2099-0026)共同资助。

P631

A

1000-1441(2015)05-0569-13

10.3969/j.issn.1000-1441.2015.05.010