基于解析误比特率的空间调制系统配置优化
2015-06-15张继良胡留军
王 洋,汪 洋,张继良,胡留军
(1.哈尔滨工业大学深圳研究生院,518055广东深圳;2.中兴通讯股份有限公司,518055广东深圳)
基于解析误比特率的空间调制系统配置优化
王 洋1,汪 洋1,张继良1,胡留军2
(1.哈尔滨工业大学深圳研究生院,518055广东深圳;2.中兴通讯股份有限公司,518055广东深圳)
在推导空间调制(Spatial Modulation,SM)系统解析误比特率(Bit Error Rate,BER)上界的基础上,通过合理配置天线数量和调制阶数等系统参数,优化SM系统误比特性能.采用矩生成函数法给出SM系统解析BER上界,将BER解析解上界与蒙特卡洛仿真对比,验证解析BER上界的紧致性.基于紧致的解析BER上界,优化天线数量和调制阶数等SM系统主要配置参数,提升SM系统误比特性能.实验结果表明,采用QPSK信号映射配置SM系统能够获取最优的误比特性能,同时在信号调制阶数确定的前提下,通过在发射端增加发射天线数量能够在几乎不牺牲SM系统误比特性能且不增加射频链的前提下有效提升系统传输速率.
空间调制;解析误比特率;系统配置优化
作为一种新型的多输入多输出MIMO(multipleinputmultiple-output)系统,空间调制SM(spatial modulation)能够有效抑制信道间干扰,且不需要发射天线同步[1].理论分析与实际测量表明,SM系统能够采用单个射频链获得接近传统多射频链MIMO系统的误比特性能[1-2].
在相同条件下,不同配置的空间调制系统具有极大的性能差异,因此配置优化工作势在必行.然而当前文献大多针对一种或几种固定配置研究空间调制系统特点.文献[3]为空间调制设计一种基于最大比合并MRC(maximal ratio combining)接收机,在独立同分布瑞利衰落信道下以4×4天线阵列16QAM信号调制及2×4天线阵列32QAM信号调制等系统配置对MRC接收机进行性能分析.文献[4]将极大似然ML(maximum likelihood)接收机引入SM,在独立同分布瑞利衰落信道以4×4天线阵列BPSK信号调制的系统配置比较SM与V-BLAST误码性能.文献[5-6]从基站能源效率方面分析SM,以2×1天线阵列及8×1天线阵列等系统配置比较分析SM与MIMO能耗.文献[7-8]以2×2天线阵列及8×4天线阵列等系统配置研究SM调制中的空间位移键控SSK(space shift keying)调制性能.目前基于性能分析结果对空间调制系统配置优化的工作并不多见.文献[9-10]分析了多种空间调制系统配置,同时表明在进行空间调制系统配置时,在传输速率一定的前提下存在一组发射天线数量与信号调制阶数的配置使系统具有最好的误比特性能,然而,仅论证了最优系统配置的存在性,并没有给出具体的最优系统配置方案.
考虑到系统接收机基带处理的复杂度,本文在调制阶数不超过64的前提下讨论空间调制系统配置优化[11].首先,给出了空间调制系统的系统架构,明确空间调制系统的信息传输方式.其次,给出任意配置空间调制系统误比特概率的解析解,并通过仿真验证解析解的紧致性.在此基础上,基于空间调制BER上界解析分析发射天线数量与信号调制阶数等空间调制系统配置参数对误比特性能的影响,建立误比特性能与空间调制系统配置参数的对应关系,进而优化空间调制系统配置.
1 空间调制系统
空间调制使用两种信息流传输信息:一种是复信号星座图中的符号位置;另一种是发射天线阵列中的天线序号,信息传输速率由信号调制阶数和发射天线数量共同决定.在发射端,空间调制系统使用单射频链进行信息传输,每次只激活发射天线阵列中的一根天线,阵列中的其他天线处于休眠状态.
对于发射天线数为Nt,接收天线数为Nr,调制阶数为M的空间调制系统,假设某次发射,发射端使用第j根发射天线发送第q个符号,即发送端发送向量为(j,q).每次发射由发射天线位置携带log2(Nt)比特信息,由符号位置携带log2(Nt)比特信息,即传输速率为log2(MNt)bpcu(bits per channel use).在接收端,采用极大似然解调算法得出发送向量的估计值(^j,^q).
以图1所示的4×2BPSK空间调制系统为例,发射天线数为4根,则每次发射由发射天线序号携带信息为2 bits;调制阶数为2,每次发射由发送符号位置携带信息为1bit,即信息传输速率为3 bpcu.
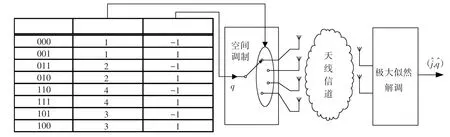
图1 典型4×2 QPSK空间调制系统
2 解析误比特性能分析
空间调制系统比传统调制增加一个维度,即发射天线位置信息所代表的维度,其误比特率上界为[4]

式中:Piq为在一次发射中使用第j根发射天线发射第q个符号的概率;N(siq,s^j^q)为sjq与s^j^q的汉明距离;k为一次发射所携带比特数,即信息传输速率;siq代表在发送端使用第j根发射天线发射第q个符号;s^j^q为通过极大似然估计得到的解调信号;s^j^q为成对差错概率PEP(pair-wise error probability).由空间调制原理可知,信息传输速率k由发射天线数量Nt和信号调制阶数M共同决定,即

假设发送信号概率相同,即

在瑞利信道下,将式(2)、(3)及文献[4]的Eq.(7)代入式(1),整理可得空间调制误比特概率解析解为
使用蒙特卡洛仿真对比验证式(4)中误比特概率解析解的紧致性.仿真条件为k=6 bpcu、Nr=8,仿真结果如图2所示.

图2 SM解析解与蒙特卡洛仿真对比
由图2可见,在信噪比较大时,空间调制系统解析误比特率上界紧致收敛于蒙特卡洛仿真结果.在误比特率小于10-3时,解析误比特率上界与蒙特卡洛仿真得到的误比特率基本重合.受到计算能力的限制,采用蒙特卡洛仿真分析系统性能过于耗时,本文基于解析误比特率上界优化空间调制系统配置.
3 系统配置优化
由式(4)可以看出,空间调制性能取决于发射天线数Nt、接收天线数Nr、调制阶数M、信噪比SNR、信息传输速率k及和信号映射方式(本文只研究PSK和QAM).可以预见,系统误比特性能随信噪比、接收天线数的增加而显著提升,随传输速率的增加而下降,QAM系统性能优于同阶PSK系统性能.然而接收天线内置于移动终端,其数量对终端的成本及体积影响巨大,接收信噪比及信息传输速率的增大也会对系统提出更高要求.同时,基于空间调制的单射频链特性,及天线的低廉成本,空间调制系统基站端的发射天线阵列规模大小对系统成本及功耗负担差别不大[5-6,9].因此,本文主要优化发射天线数Nt和调制阶数M.
3.1 相同传输速率下系统配置优化
由式(2)可知,数据传输速率k一定时,发射天线数Nt与调制阶数M乘积为常数,MNt=2k,即Nt与M成对出现.因此当k为常数时,Nt与M为一一对应的关系.
1)在传输速率和接收天线数量相同、信噪比不同的前提下,优化发射天线数Nt和调制阶数M.PSK和QAM空间调制误比特率与发射天线数量的关系如图3所示,其中传输速率k=6 bpcu,Nr=8,信噪比SNR分别为10、15、20和25 dB.

图3 不同信噪比下系统误比特率与发射天线数量的关系
由图3可见,在确定传输速率和接收天线数量前提下,当调制阶数大于4时,任意信噪比空间调制系统误比特率随发射天线数量增加而降低,QPSK调制的SM可获得最优的误比特性能.此外,虽然接收信噪比对空间调制系统误比特性能影响巨大,但依然存在一些分配方案能够以低信噪比获得更优的误比特性能.
2)在传输速率和信噪比相同、接收天线数不同的前提下,优化发射天线数Nt和调制阶数M.PSK和QAM空间调制误比特率与发射天线数量的关系如图4所示,其中k=6 bpcu,SNR=20 dB,接收天线数Nr分别为2、4、8和16.
由图4可见,在确定数据传输速率和信噪比前提下,当调制阶数大于4时,任意接收天线数空间调制系统误比特率随发射天线数量增加而降低,其中采用QPSK调制的SM可获得最优的误比特性能.此外,虽然接收天线数量对空间调制系统误比特性能影响巨大,但依然存在一些分配方案能够以少量接收天线获得更优的系统性能.
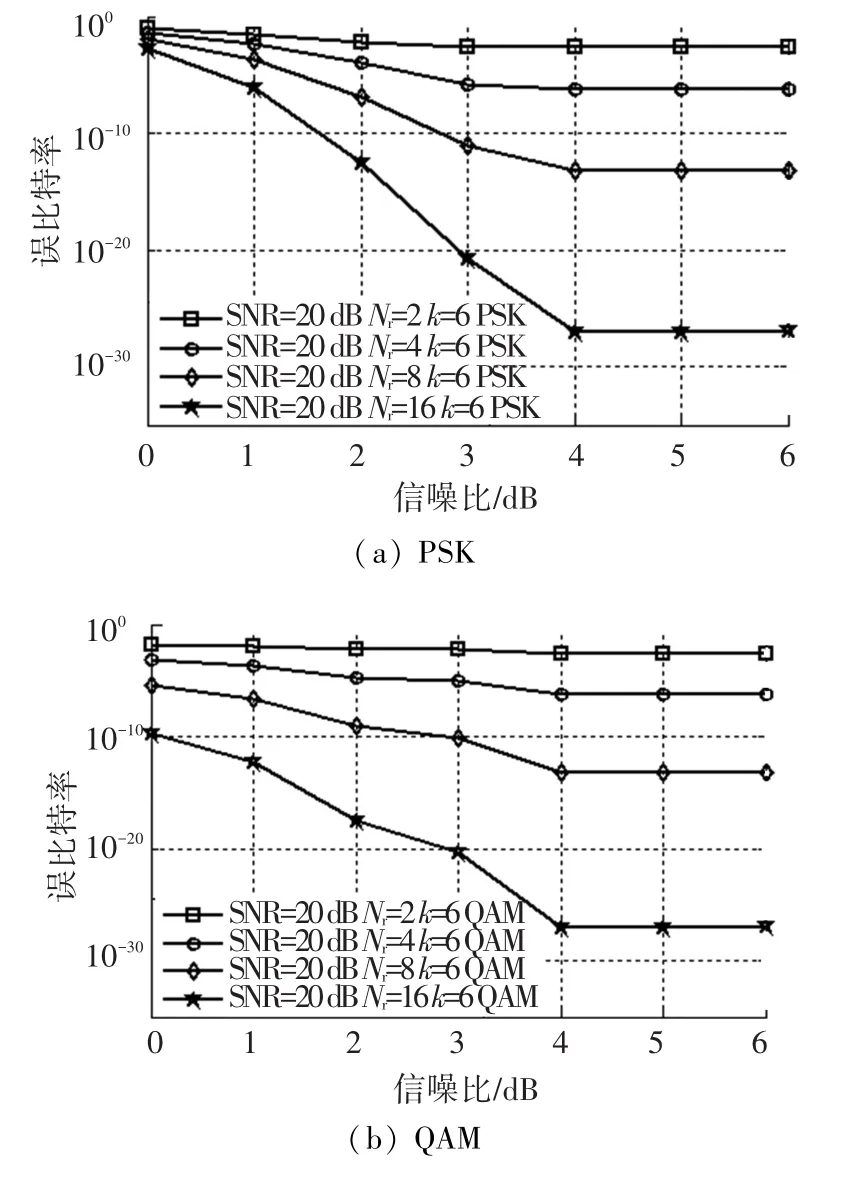
图4 不同接收天线数系统误比特率与发射天线数量的关系
3)在相同条件下对比分析使用不同调制方式的空间调制系统性能.PSK和QAM空间调制误比特率与发射天线数量的关系如图5所示,其中Nr=8,k=6 bpcu,SNR=20 dB.

图5 不同信号映射方式系统误比特率与发射天线数量的关系
由图5可见,在确定数据传输速率、接收天线数量和信噪比前提下,当调制阶数大于4时,PSK和QAM两种信号映射方式的空间调制系统误比特率均随发射天线数量增加而降低,QPSK调制的MIMO都能获得最优的误比特性能.此外,由于高阶QAM信号调制的性能优于PSM信号调制,而这两种信号映射方式的空间调制系统均于调制阶数为4时具有最优的误比特性能.因此,相较于QAM空间调制系统,PSK空间调制系统性能受发射天线数量的影响更大.值得注意的是,QAM空间调制并不总是优于PSK空间调制.当调制阶数为8时,PSK空间调制系统误比特性能优于QAM空间调制系统.
4)在接收天线数和信噪比相同,任意确定数据传输速率的前提下,优化发射天线数Nt和调制阶数M.PSK和QAM空间调制误比特率与发射天线数量的关系如图6所示,其中Nr=8,SNR=20 dB,传输速率k分别为5、6、7和8 bpcu.

图6 不同数据传输速率系统误比特率与发射天线数量的关系
由图6可见,在确定接收天线数量和信噪比的前提下,任意传输速率的SM系统误比特性能均随发射天线数量增加而显著改善,QPSK调制的SM可获得最优的误比特性能.此外,虽然传输速率对空间调制系统误比特性能影响巨大,但依然存在一些分配方案能够以高传输速率获得更优的误比特性能.
由此可知,当确定数据速率k情况下,任意固定数据速率、信噪比、接收天线数、信号映射方式的SM系统误比特性能均随发射天线数量增加而显著改善,且采用QPSK信号调制的系统配置为最优配置.即当数据速率k一定,发射天线数量不受限制时,应优先采用多发射天线数配置方案,且采用2k/4根发射天线、QPSK信号映射的空间调制系统具有最优的误比特性能.
3.2 相同发射阵列下系统配置优化
由式(2)可知,固定发射天线数量,增加调制阶数可以增加传输速率k.在发射天线数量、接收天线数量、信噪比相同,传输速率不同前提下,优化系统配置.PSK和QAM空间调制误比特率与调制阶数的关系如图7所示,其中Nr=8,SNR=20 dB,Nt分别为2、4、8和16.

图7 相同发射阵列系统误比特率与发射天线数量的关系
由图7可见,固定发射天线数量,以调制阶数增加传输速率时,SM系统性能随调制阶数增加而下降,调制阶数大于4时SM系统性能显著下降.即当发射天线数量为常数时,SSK系统具有最低的误比特率.然而,SSK系统与QPSK空间调制系统的性能差异很小.综合考虑数据传输速率与误比特性能,应采用QPSK信号映射配置空间调制系统.
3.3 相同调制阶数下系统配置优化
由式(2)可知,固定调制阶数,增加发射天线数可以增加传输速率k.在调制阶数、接收天线数量、信噪比相同,传输速率不同前提下,优化系统配置.图8为PSK和QAM空间调制误比特率与调制阶数的关系,其中Nr=8,SNR=20 dB,传输速率k分别为5、6、7和8 bpcu.
由图8可见,调制阶数相同,不同传输速率的PSK空间调制系统性能基本一致,QAM空间调制系统性能相近.即在信号调制阶数确定的前提下,通过在发射端增加发射天线数量,能够在几乎不牺牲SM系统误比特性能且不增加射频链的前提下有效提升系统传输速率.

图8 不同数据传输系统速率误比特率与发射天线数量的关系
4 结 论
1)当固定传输速率时,应采用QPSK信号映射配置空间调制系统.
2)当发射天线数量为常数时,采用SSK调制可使系统具有最好的误比特性能,但综合考虑数据传输速率与误比特性能应采用QPSK信号映射的空间调制系统.
3)在信号调制阶数确定的前提下,通过在发射端增加发射天线数量,能够在几乎不牺牲SM系统误比特性能且不增加射频链的前提下有效提升系统传输速率.
[1]RENZOM D,HAASH,GRANTPM.Spatialmodulation for multiple antenna wireless systems:a survey[J].IEEE Communications Magazine,2011,49(12):182-191.
[2]ZHANG J,WANG Y,DING L,et al.Bit error probability of spatialmodulation over measured indoor channels[J]. IEEE Transactions on Wireless Communications,2014,13(3):1380-1387.
[3]MESLEH R Y,HAAS H,SINANOVIC,et al.Spatial modulation[J].IEEE Transactions on Vehicular Technology,2008,57(4):2228-2241.
[4]JEGANATHAN J,GHRAYEBA,SZCZECINSKIL.Spatial modulation:optimal detection and performance analysis[J].IEEE Communications Letters,2008,12(8):545-547.
[5]STAVRIDIS A,SINANOVIC S,RENZO M D,et al.An energy saving base station employing spatial modulation[C]//Proc.IEEE International Workshop on Computer Aided Modeling and Design of Communication Links and Networks.2012:231-235.
[6]STAVRIDIS A,SINANOVIC S,RENZO M D,et al. Energy evaluation of spatialmodulation at a multi-antenna base station[C]//Proc.IEEE Vehicular Technology Conference-Fall.2013:1-5.
[7]JEGANATHAN J,GHRAYEB A,SZCZECINSKIL,et al. Space Shift Keying modulation for MIMO channels[J]. IEEE Transactions on Wireless Communications,2009,8(7):3692-3703.
[8]RENZO M D,LEONARDIS D D,GRAZIOSI F,et al. Space Shift Keying(SSK-)MIMO with practical channel estimates[J].IEEE Transactions on Communications, 2012,60(4):998-1012.
[9]RENZO M D,HAAS H.On transmit-diversity for spatial modulation MIMO:impact of spatial-constellation diagram and shaping filters at the transmitter[J].IEEE Transactions on Vehicular Technology,2013,62(6):2507 -2531.
[10]RENZO M D,HAASH.Bit error probability of SM-MIMO over generalized fading channels[J].IEEE Transactions on Vehicular Technology,2012,61(3):1124-1144.
[11]GOGOIP,SARMA K K.STBC coded MISO and MIMO setup in frequency selective wireless fading channels for BPSK and QPSK modulation schemes[C]//National Conference on Computational Intelligence and Signal Processing.2012:158-164.
(编辑王小唯)
Configuration optim ization of spatialmodulation based on analytical bit error rate
WANG Yang1,WANG Yang1,ZHANG Jiliang1,HU Liujun2
(1.Shenzhen Graduate School,Harbin Institute of Technology,518055 Shenzhen,Guangdong,China;2.Zhongxing Telecommunication Equipment Corporation,518055 Shenzhen,Guangdong,China)
Based on the analytical Bit Error Rate(BER)upper bound of Spatial Modulation(SM)systems,the optimal configuration of SM by allocating properly of the information bits onto spatial and signal constellation diagrams is investigated.The analytical BER upper bound of SM systems is derived by employing the moment generating function method.The tightness of the upper bound is verified by a comparison to Monte-Carlo simulations.The antenna number and modulation order of SM systems are optimized based on the upper bound of analytical BER.It is shown that,the Quadrature Phase Shift Keying(QPSK)signal mapping is the optimal constellation in SM systems in terms of BER.Also,a SM system with a given signal constellation can increase the transmission rate without sacrificing BER performance and adding Radio Frequency(RF)chains by increasing the number of transmit antennas.
spatialmodulation;analytical bit error rate;configuration optimization
TN929
:A
:0367-6234(2015)11-0047-06
10.11918/j.issn.0367-6234.2015.11.008
2014-09-17.
国家自然科学基金项目(61371101);深圳市生物、互联网、新能源、新材料产业发展专项资金项目(JC201104210030A);深圳市科技计划项目(JC200903120174A);哈工大校科研创新基金项目(HIT.NSFIR.2010133);欧盟FP7项目(318992).
王 洋(1983—),女,硕士研究生;汪 洋(1977—),男,副教授,博士生导师.
王 洋,wangyang30000@163.com.
