改进Twisting算法的相对位姿耦合控制

耿云海，陈炳龙，梁海朝

（1.哈尔滨工业大学卫星技术研究所，150080哈尔滨；2.北京航天长征飞行器研究所，100076北京）

改进Twisting算法的相对位姿耦合控制

耿云海1，陈炳龙1，梁海朝2

（1.哈尔滨工业大学卫星技术研究所，150080哈尔滨；2.北京航天长征飞行器研究所，100076北京）

为实现对非合作目标航天器进行在轨服务，将Twisting算法与线性补偿项相结合，设计相对位置与姿态耦合的二阶滑模控制器.以航天器对接端口间耦合相对运动模型为基础，设计两种滑模平面的改进Twisting控制器.选取严格李雅普诺夫函数，证明所设计的改进Twisting控制器对有界干扰具有有限时间收敛的特性，并估计出收敛时间的上界.设计数学仿真，将其与标准Twisting算法进行对比，验证所设计的二阶滑模控制器对模型不确定性及有界干扰具有较强的鲁棒性，并能够有效抑制执行机构的震颤.

航天器在轨服务；Twisting算法；线性补偿；滑模平面；严格李雅普诺夫函数

众所周知，真实物理系统中含有不确定性、空间环境中存在扰动作用，这些因素使得控制系统设计变得更加复杂.针对这类问题，发展出自适应控制［1-2］、鲁棒控制［3-4］、滑模控制［5-7］等方法，抑制不确定性及干扰.其中，自适应控制通过增加控制器参数、动态计算控制器的增益，使系统对不确定性及干扰具有一定的鲁棒性；但计算量随着参数维数的增加而变大［8］.鲁棒控制算法则通过扩展含有不确定性的状态变量，利用增广系统设计控制器来增强系统对不确定性的鲁棒性；但随着增广变量的增加计算量也随之加大.文献［9］建立了增广状态的系统方程，基于航天器质心间相对运动关系设计鲁棒控制器，但该相对运动模型属于点质量模型，忽略了相对转动对相对平动的耦合作用.

滑模变结构控制方法独立于系统动力学特性，且对已知界限的不确定性及干扰具有鲁棒性.利用已知不确定性及扰动的上确界设计滑模平面，将系统状态约束在滑模平面内.当系统轨迹运动到滑模平面以后，系统响应将不受不确定性和扰动的影响，只由滑模平面唯一决定.因此，滑模控制器对有界的不确定性及干扰具有较强的鲁棒性.但标准滑模控制器只适用于系统输出的相对阶为1的情况［10］，且在高频开关切换下产生震颤效应.为降低震颤现象，文献［11］提出高阶滑模算法，在保证系统特性的基础上，通过改变间断面附近区域内的动力学模型来避免中断.高阶滑模算法继承了标准滑模控制器的优点，并且利用状态偏差对时间的高阶导数解决了相对阶的限制，既有效地减弱震颤，又改善开关延迟和离散测量对控制精度产生的影响［12］.然而，高阶滑模控制器所需的信息量随滑模相对阶数的增加而增大（r阶滑模控制器需要计算s、˙s、…、s（r-1））．具备有限时间收敛特性的任意阶滑模控制器仍然处于理论研究［13］，但2阶滑模控制器已经成功解决了现实问题.被广泛应用的2阶滑模算法有：Twisting［14-15］、Super Twisting［16-17］和终端滑模算法［18］.文献［14］利用严格李雅普诺夫函数证明了标准Twisting算法的收敛特性.将其与线性控制算法进行对比：二阶滑模算法对距离原点较近的有界干扰具有强鲁棒性；线性算法处理距离原点较远的有界扰动能力更强［19］.因此，在Twisting算法中加入线性补偿项能有效改善闭环系统特性，减弱执行机构的震颤效应.

本文考虑相对转动对相对平动的耦合作用，利用文献［20-21］建立的航天器非质心点间耦合动力学模型，将标准Twisting控制与线性算法相结合，以两种滑模平面分别设计含线性补偿项的改进Twisting控制器，并选取严格李雅普诺夫函数证明其对有界干扰具有有限时间收敛的特性.利用数学仿真，将其与标准Twisting控制器进行对比，验证所建立的姿轨耦合控制器对有界干扰具有更强的鲁棒性，可以有效减弱执行机构震颤效应，提高对非合作目标航天器进行在轨服务的可靠性.

1 相对运动动力学模型

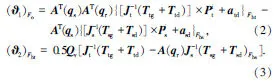
图1 两航天器对接端口间相对运动关系

假设干扰加速度ad是连续可导的有界慢变函数，干扰力矩Td［22］、重力梯度力矩Tg分别为如下形式：

其中：ad0是干扰加速度的初值，kd为常数；ωo为轨道角速度的模；r是地心矢径的模，Z0为单位地心矢径．

2 二阶滑模控制器设计

2.1 标准Twisting控制器

令滑模状态为s，记x=s、y=˙s．闭环系统状态方程形式如下：

其中｜μ｜≤D．

由Twisting算法可知，当α-D＞β＞D成立时系统（4）可在有限时间内收敛到平衡点．

记期望状态为xd，状态偏差e=x-xd．取滑模平面s=e，由Twisting算法设计式（1）的姿轨耦合控制器T1形式如下：

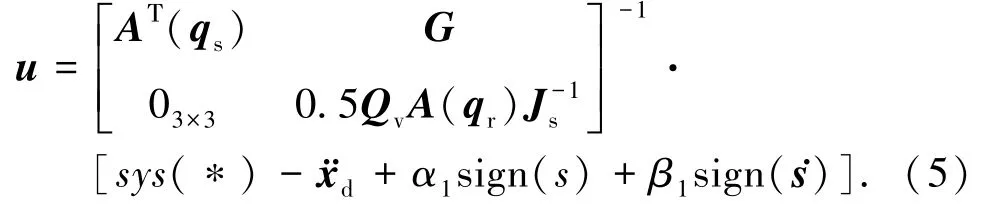
其中，α1、β1为主对角线矩阵．由式（2）、式（3）及扰动力矩Td、Tg的形式可知，δ连续可导且有界．

取滑模平面s=˙e+λe，λ为正常数组成的主对角线矩阵，由Twisting算法设计式（1）的姿轨耦合控制器T2形式如下：

记X=s、Y=˙s，得到闭环系统方程为

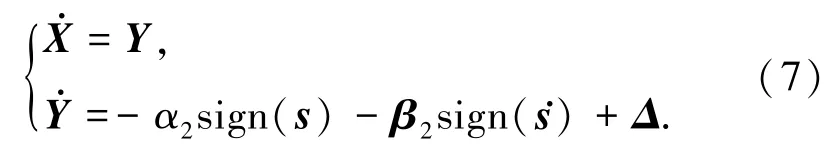
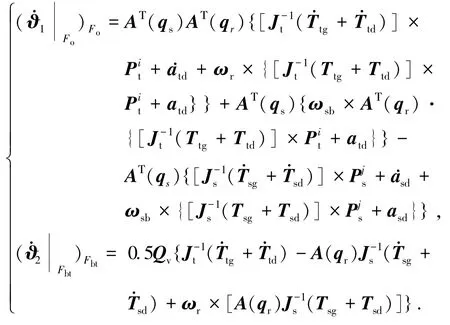
因此，｜Δi｜≤χi，当α2i-χi＞β2i＞χi时系统（6）也可在有限时间内收敛到平衡点．其中，

2.2 改进Tw isting控制器

为改变闭环系统特性，将Twisting算法与线性补偿项相结合，得到如下闭环系统方程：

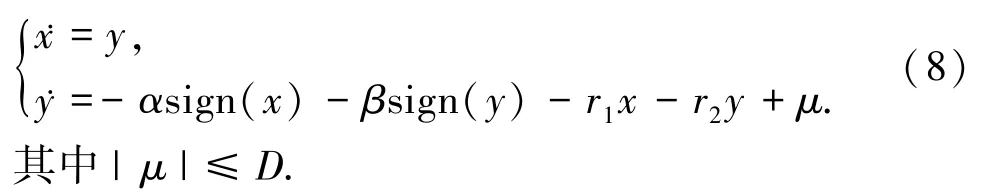
选取严格李雅普诺夫函数如下：

对W（x，y）进行放大处理得

其中，

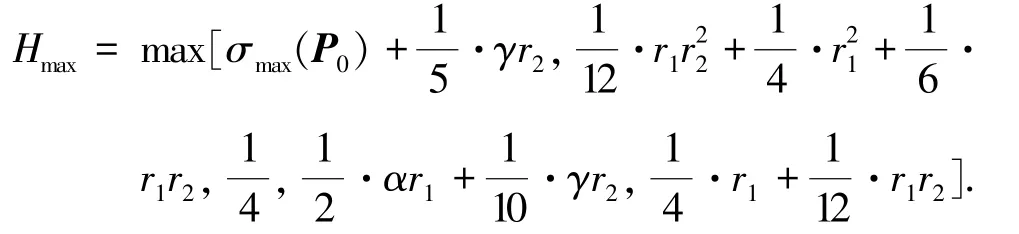
对W求时间的一阶导数得

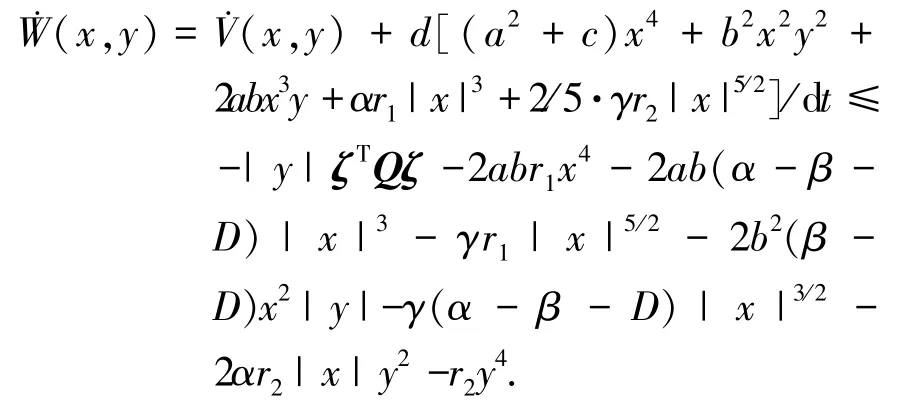
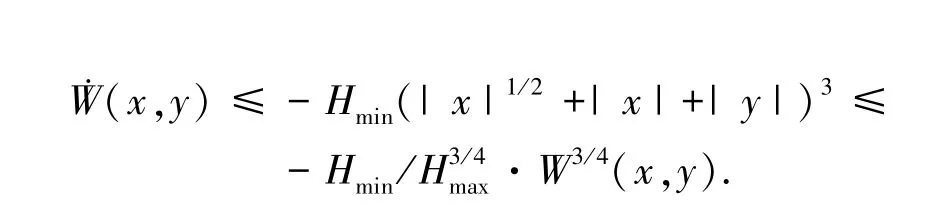
其中，

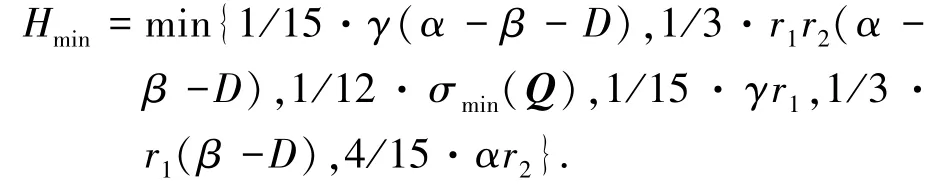
求解如下微分方程：

因此，系统（8）收敛到原点的时间上限Tf为

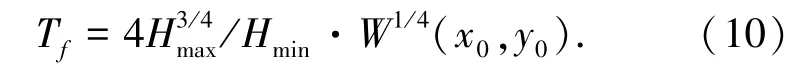
2.3 改进的姿轨耦合控制器

取滑模平面为s=e时，设计基于改进Twisting算法的姿轨耦合控制器M1，形式如下：

令X=s，Y=˙s；则闭环系统状态方程为

由2.1节可知，当M1i-Εi＞M2i＞Εi，M3i，M4i＞0时系统（12）在有限时间内收敛到平衡点．

取滑模平面为s=˙e+λe时，设计基于改进Twisting算法的姿轨耦合控制器M2形式如下：

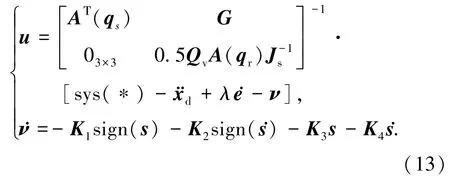
令X=s，Y=˙s，Δ=˙δ；则闭环系统状态方程为

由2.1节可知，当K1i-χi＞K2i＞χi，K3i，K4i＞0时系统（14）在有限时间内收敛到平衡点．

分析上述控制的设计过程：M1控制器直接抑制有界干扰，M2控制器则通过抑制干扰对时间的导数来提高鲁棒性．因此，M1对相对位置的控制精度高于M2，而M2对相对速度的控制精度高于M1．

3 数学仿真

3.1 仿真参数

S与T的轨道六根数如表1所示，两航天器质量为：ms=240 kg，mt=320 kg；转动惯量为

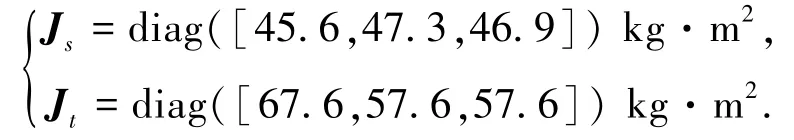
对接端口位置矢量在各自体系下表示为

表1 试件主要参数S和T的轨道参数

初始姿态四元数和姿态角速度的初值为

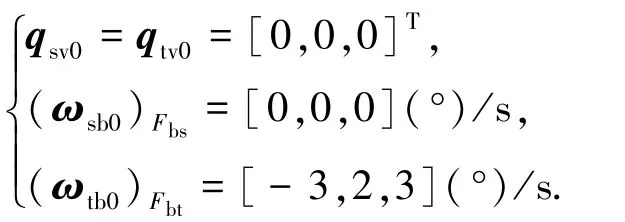
采用双组元轨道和姿态发动机做为执行机构，控制力与力矩的输出限制分别为amax=0.2 m／s2和Tmax=0.8 N·m.干扰加速度为：

假设相对位置、相对速度、相对姿态角速度均由状态估计器给出，仿真实验目的是验证所设计姿轨耦合控制器对有界干扰的鲁棒性，因而不考虑敏感器测量误差影响.分别设计控制器T1、T2、M1、M2使与实现安全对接，具体参数如表2所示．

表2 控制器参数

3.2 仿真结果

选取不同形式的干扰加速度分别进行仿真，将150 s到200 s仿真时间内数据的平均值与其三倍标准方差之和定义为标准Twisting算法的控制精度；将50 s到100 s仿真时间内数据的平均值与其三倍标准方差之和定义为改进Twisting算法的控制精度.由于M1，M2对不同形式干扰的控制效果相似，这里仅给出有界线性增长干扰作用下的仿真结果，图2～6为M1控制效果，图7～11为M2控制效果．计算T1、M1与T2、M2的控制精度如表3所示．

图2 M1在有界线性增加干扰作用下的相对平动关系曲线（Fbs）

图中，x、y、z为对接端口间相对位置分量，Vx、Vy、Vz为对接端口间相对速度分量；φr、θr、ψr为相对姿态角分量；ωrx、ωry、ωrz为相对姿态角速度分量；｜ρij｜为对接端口之间的距离，｜ρ00｜为航天器质心间距离；Fcx、Fcy、Fcz为姿轨发动机输出控制力分量；Tcx、Tcy、Tcz为姿轨发动机输出控制力矩分量；相对姿态角速度分量；Sx、Sy、Sz是由相对平移关系组成的滑模面分量，Sq1、Sq2、Sq3是由相对四元数矢部组成的滑模面分量．

图3 M1在有界线性增加干扰作用下的相对转动关系曲线（Fbt）

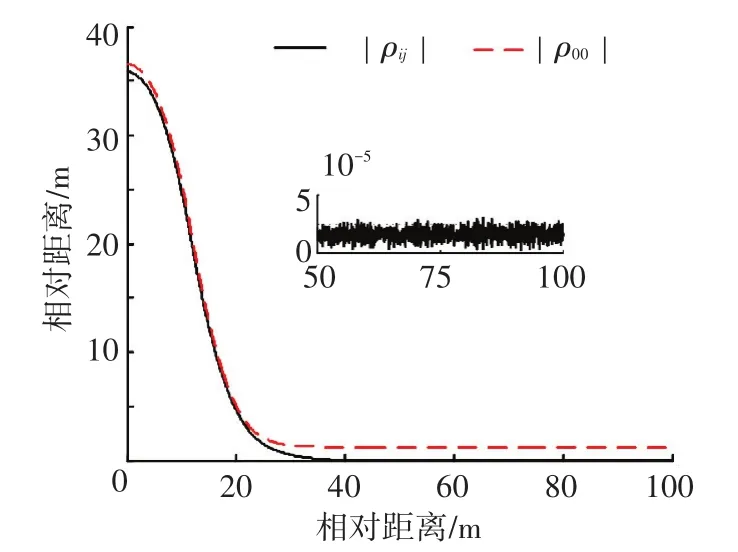
图4 M1在有界线性增加干扰作用下的相对距离关系曲线

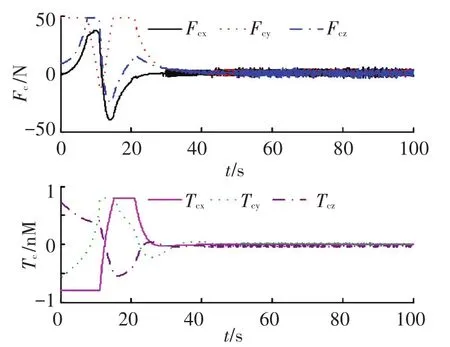
图5 M1在有界线性增加干扰作用下的执行机构输出关系曲线（Fbs）

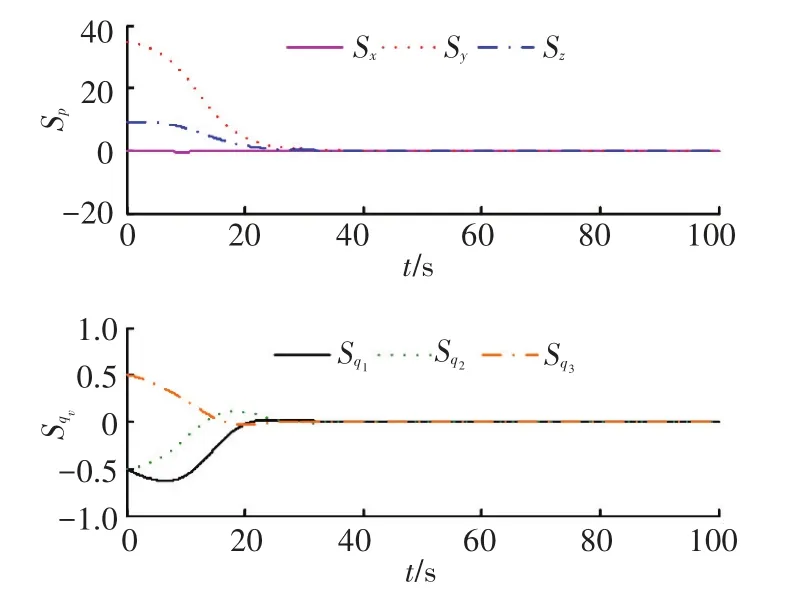
图6 M1在有界线性增加干扰作用下的控制器滑模平面

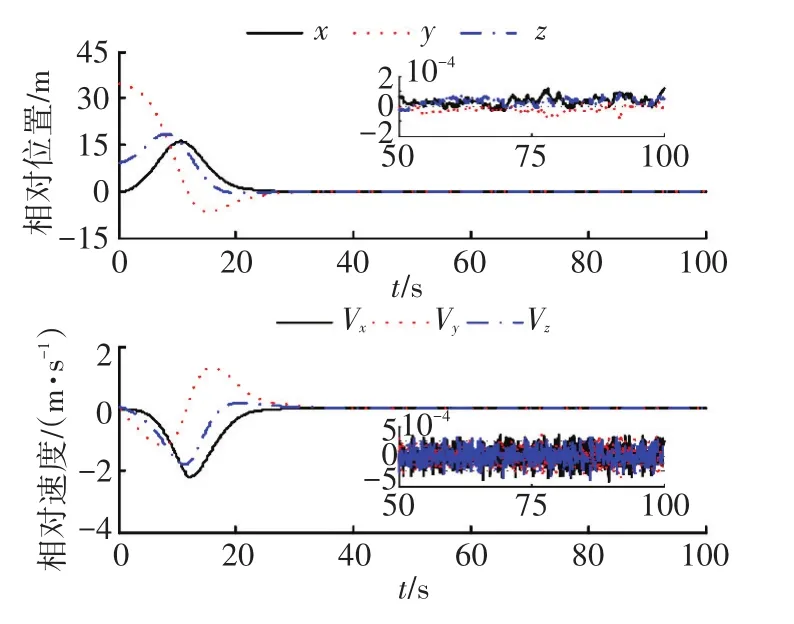
图7 M2在有界线性增加干扰作用下的相对平动关系曲线（Fbs）

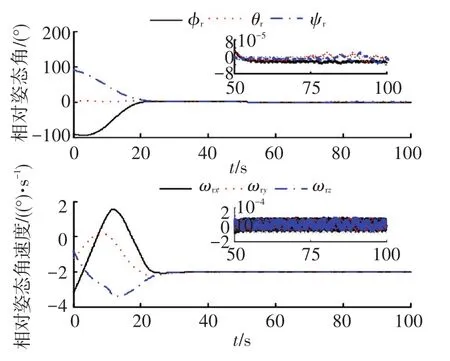
图8 M2在有界线性增加干扰作用下的相对转动关系曲线（Fbt）

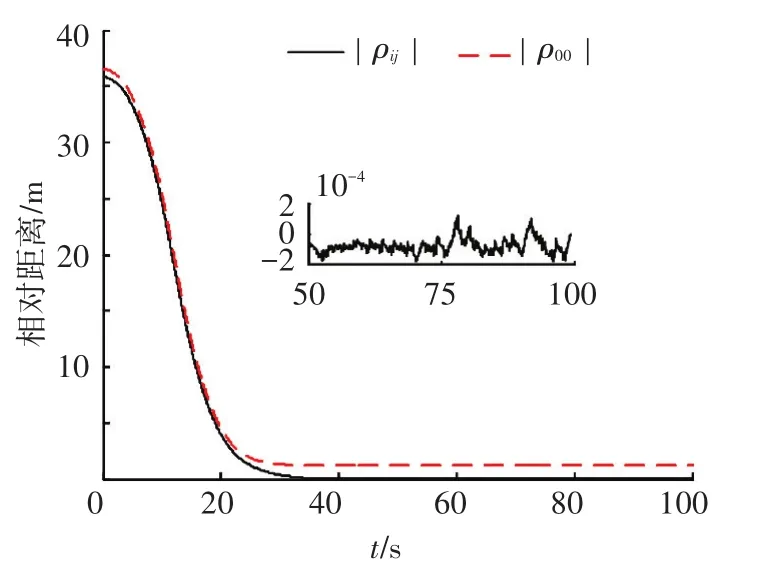
图9 M2在有界线性增加干扰作用下的相对距离关系曲线

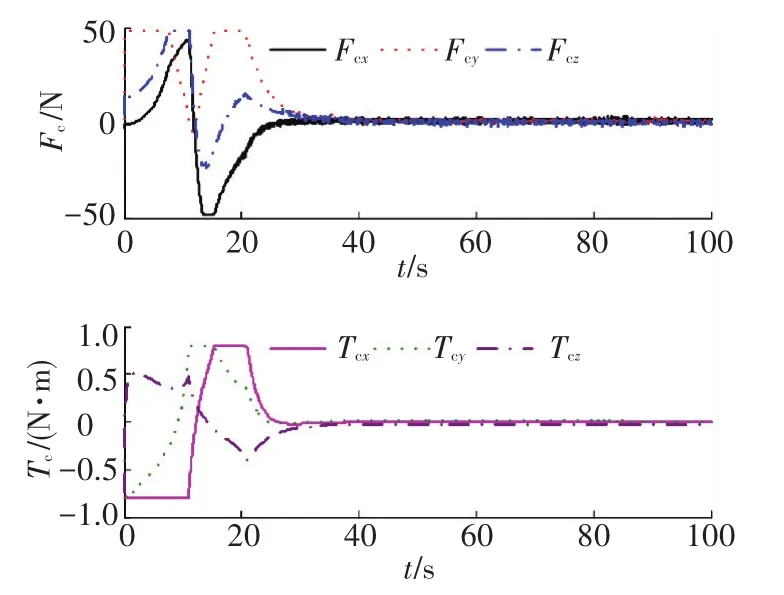
图10 M2在有界线性增加干扰作用下的执行机构输出关系曲线（Fbs）

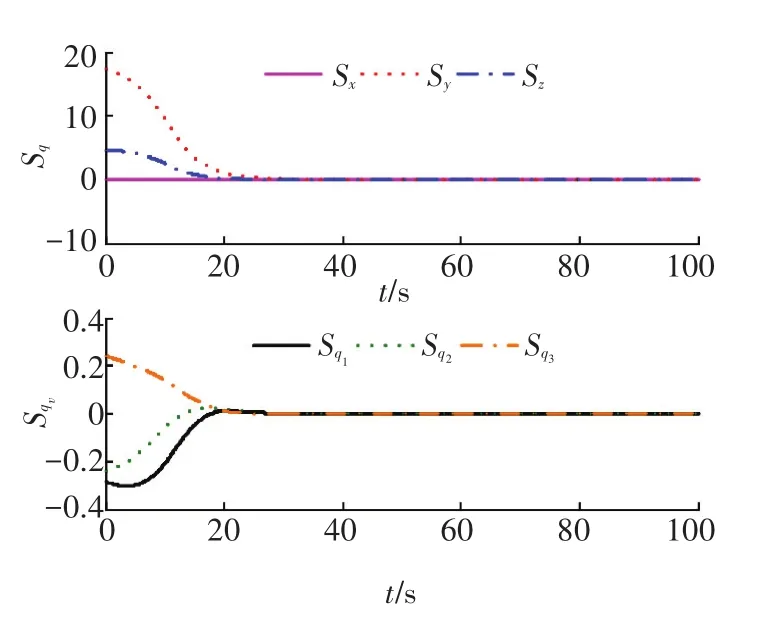
图11 M2在有界线性增加干扰作用下的控制器滑模平面

T1与M1仿真结果对比可见，含线性补偿项的改进Twisting控制器M1对有界干扰的抑制能力更强，收敛速度更快．对比表3的计算结果，M1对各个相对运动状态的控制精度以及消除执行机构震颤效应等方面都远远优于标准Twisting控制器T1．类似地，T2与M2仿真结果对比后可以得出相似结论：M2对有界干扰的抑制能力更强，收敛速度更快，且M2的控制精度及消除执行机构震颤效应等方面也都远远优于T2．综上所述，含线性补偿项的M1、M2控制器可以有效抑制不确定性和有界干扰，使系统具有更强的鲁棒性；同时，显著改善了执行机构因高频切换而产生的震颤效应，提高了标准Twisting算法的性能，同时继承了滑模控制器在有限时间收敛到平衡点的特性．

对比控制器M1、M2的仿真结果可知，M1对相对位置的控制精度高于M2，而对相对速度的控制精度低于M2．由此证明了2.3节对控制器的特性分析：控制器M1抑制式（12）中的有界干扰δ，直接针对δ进行补偿；M2则通过抑制式（14）中有界的干扰变化率Δ来补偿有界干扰δ对系统的影响．

3.3 参数不确定性的鲁棒性验证

选取转动惯量参数，对Js、Jt进行正负拉偏10%，利用控制器M1、M2分别进行仿真，验证所设计的二阶滑模控制器对模型参数不确定性的鲁棒性.计算70 s到100 s内的控制精度，如表4～7所示.由仿真结果可见：M1对相对位置和姿态角的控制精度数量级不变，相对速度和姿态角速度精度有所降低；M2与之相反，相对位置和姿态角的控制精度有所下降，但仍比标准Twisting算法的精度高一或两个数量级，相对速度和姿态角速度的控制精度数量级不变.由此可见，本文所设计的带线性补偿器的二阶滑模控制器对模型参数不确定性有较强的鲁棒性.

表3 控制器精度对比

表4 Js+10%，Jt+10%的控制精度

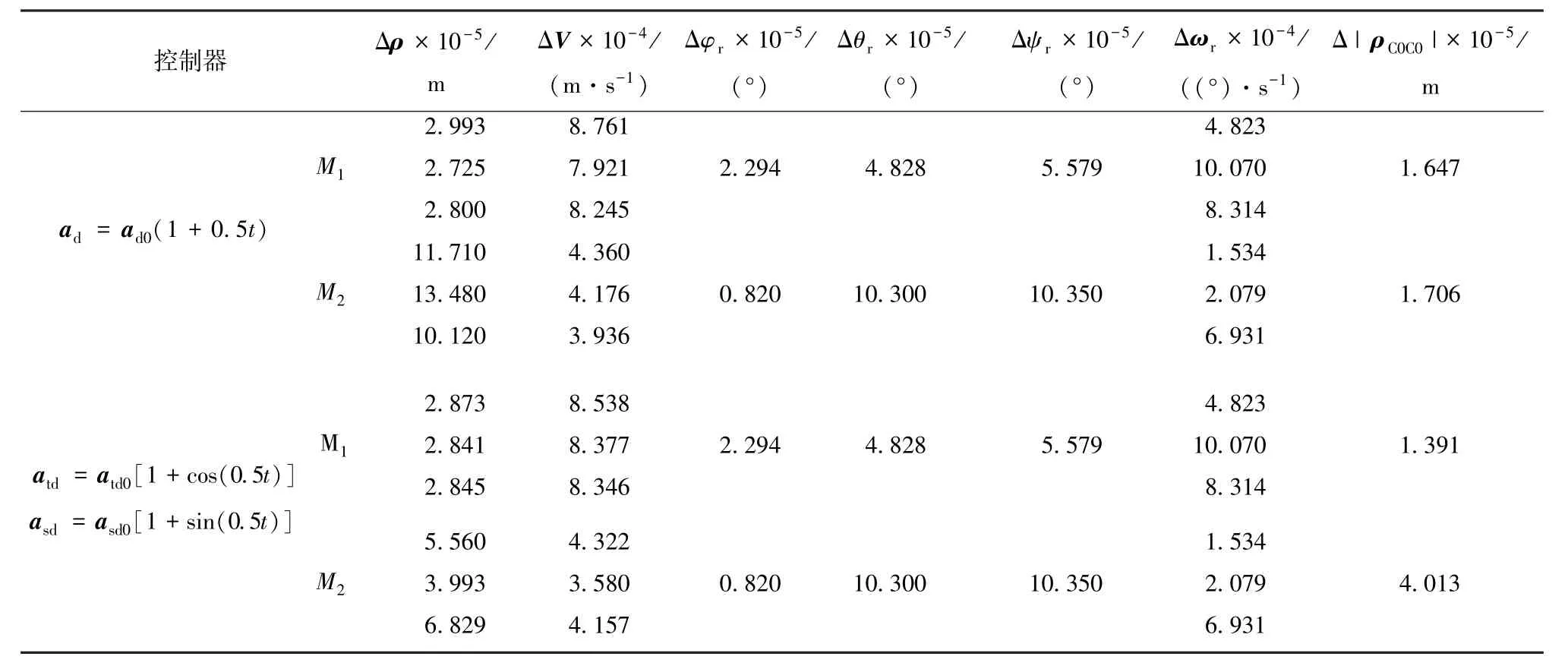
表5 Js+10%，Jt-10%的控制精度

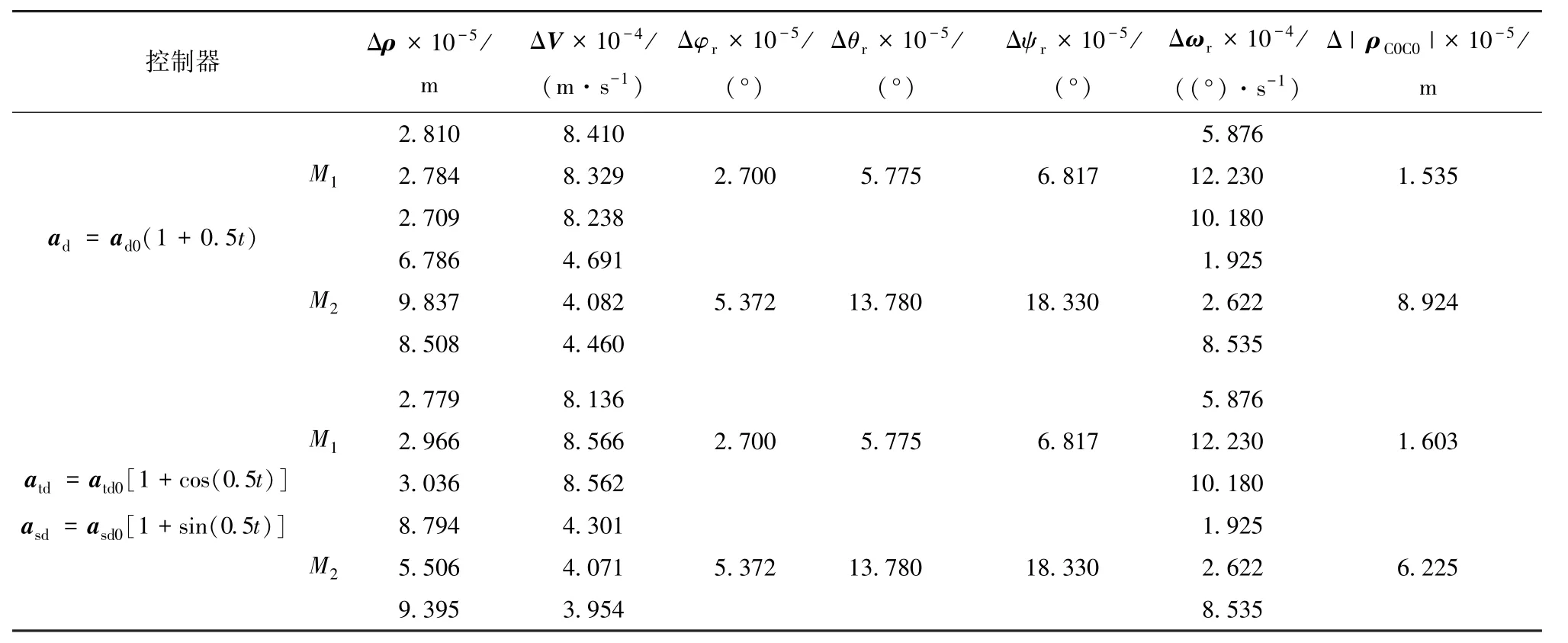
表6 Js-10%，Jt+10%的控制精度

表7 Js-10%，Jt-10%的控制精度

综上所述，仿真结果证明包含线性补偿项的改进Twisting控制器对有界干扰及模型参数不确定性具有强鲁棒性，并且达到较高的控制精度，足以保证与非合作目标航天器对接端口间安全对接.

4 结 论

1）考虑相对转动对相对平动的耦合作用，以航天器对接端口间耦合相对运动动力学模型为基础，利用两种形式的滑模平面分别设计含线性补偿项的改进Twisting控制器，实现航天器相对位置与姿态协同控制，进而满足对失控的非合作目标航天器进行在轨服务的要求.

2）选取严格李雅普诺夫函数，证明所设计的含有线性补偿项的改进Twisting控制器在有界干扰作用下不仅是全局渐进稳定的，还具备在有限时间内收敛到平衡点的特性.此外，给出了通过求解李雅普诺夫函数计算收敛时间上界的方法.

3）利用MATLAB-Simulink建立对比仿真，验证所设计的改进Twisting控制器不但对有界不确定性具有较强的鲁棒性，并且能够有效抑制有限速率线性增长的和周期性的慢变有界干扰，仿真结果证明该改进Twisting控制器可以显著减弱执行机构因高频切换所产生的震颤效应.

后期的工作将在本文的基础上，围绕干扰及不确定性的形式深入研究减弱滑模控制器执行机构震颤效应的方法，结合自适应控制思想设计变增益的自适应相对位姿耦合控制算法.

［1］SINGLA P，SUBBARAO K，JUNKINS J L.Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty［J］.Journal of Guidance，Control，and Dynamics，2006，29（4）：892-902.

［2］XITao，LI Jiancheng，PAN Weiquan.Nonlinear adaptive feedback control for spacecraft proximity formation flying［C］／／2013 International Conference on Mechanical，Automotive and Materials Engineering.Hong Kong：Trans Tech Publications Ltd.，2013：446-450.

［3］GAO Huijun，YANG Xuebo，SHI Peng.Multi-objective robust H∞control of spacecraft rendezvous［J］.IEEE Trans.Control Syst.Technol.，2009，17（4）：794-802..

［4］GAO Xiangyu，TEO K L，DUAN Guangren.Robust H∞control of spacecraft rendezvous on elliptical orbit［J］. Journal of the Franklin Institute，2012，349（8）：2515-2529.

［5］UTKIN V I，POZNYAK A S.Adaptive slidingmode control with application to super-twist algorithm：Equivalent controlmethod［J］.Automatica，2013，49（1）：39-47.

［6］PUKDEBOON C.Second-order slidingmode controllers for spacecraft relative translation［J］.Applied Mathematical Sciences，2012，6（100）：4965-4979.

［7］PUKDEBOON C.Finite-time second-order sliding mode controllers for spacecraft attitude tracking［J］. Mathematical Problems in Engineering，2013，2013（2013）：1-12.

［8］SHTESSEL Y，TALEB M，PLESTAN F.A novel adaptivegain supertwisting sliding mode controller：Methodology and application［J］.Automatica，2012，48（5）：759-769.

［9］CLOHESSY W H，WILTSHIRE R S.Terminal guidance system for satellite rendezvous［J］.Journal of the Aerospace Sciences，1960，27（9）：653-658.

［10］LEVANT A.Sliding order and sliding accuracy in sliding mode control［J］.International Journalof Control，1993，58（6）：1247-1263.

［11］WILFRID P，JEAN P B.Sliding mode control in engineering［M］.New York：Marcel Dekker Inc，2002：51-94.

［12］LEVANT A.Principles of 2-sliding mode design［J］. Automatica，2007，43（4）：576-586.

［13］UTKIN V.About second order sliding mode control，relative degree，finite-time convergence and disturbance rejection［C］／／Proceedings of the 2010 11th International Workshop on Variable Structure Systems.Mexico City：Association for Computing Machinery，2010：528-533.

［14］SANTIESTEBAN R，FRIDMAN L，MORENO JA.Finitetime convergence analysis for＂Twisting＂controller via a strict Lyapunov function［C］／／Proceedings of the 2010 11th InternationalWorkshop on Variable Structure Systems. Mexico City：Association for Computing Machinery，2010：1-6.

［15］POLYAKOV A，POZNYAK A.Lyapunov function design for finite-time convergence analysis：“Twisting”controller for second-order slidingmode realization［J］.Automatica，2009，45（2）：444-448.

［16］VAZQUEZ C，COLLADO J，FRIDMAN L.Super twisting control of a parametrically excited overhead crane［J］. Journal of the Franklin Institute，2014，351（4）：2283-2298.

［17］MORENO JA.On strict Lyapunov functions for some nonhomogeneous super-twisting algorithms［J］.Journal of the Franklin Institute，2014，351（4）：1902-1919.

［18］HUI Liu，Li Junfeng.Terminal sliding mode control for spacecraft formation flying［J］.IEEE Transactions on Aerospace and Electronic Systems，2009，45（3）：835-846.

［19］MORENO J A，OSORIO M.A Lyapunov approach to second-order slidingmode controllers and observers［C］／／Proceedings of the 47th IEEE Conference on Decision and Control.Piscataway：IEEE，2008：2856-2861.

［20］SEGAL S，GURFIL P.Effect of kinematic rotationtranslation coupling on relative spacecraft translational dynamics［J］.Journal of Guidance，Control，and Dynamics，2009，32（3）：1045-1050.

［21］陈炳龙，耿云海.对接端口间相对运动耦合动力学建模学研究［J］.系统工程与电子技术，2014，36（4）：714-720.

［22］王炳全，崔祜涛，杨涤.轻型高精度卫星的变结构姿态控制器［J］.航空学报，2000，21（5）：417-420.

（编辑张 宏）

Relative position and attitude coupled control based on modified tw isting algorithm

GENG Yunhai1，CHEN Binglong1，LIANG Haizhao2
（1.Research Center of Satellite Technology，Harbin Institute of Technology，150080 Harbin，China；2.Beijing Institute of Space Long March Vehicle，100076 Beijing，China）

The relative position and attitude coupled second-order slidingmode controller is proposed by combining twisting algorithm with linear compensator for on-orbit servicing to a non-cooperative target spacecraft.On the basis of a coupled relativemotion model between docking ports on two spacecrafts，themodified twisting controllerswith linear compensation items are designed by using two different sliding surfaces.A strict Lyapunov function is proposed to prove that the modified twisting controllers have the property of finite time convergence for bounded perturbations and the upper bound for the time convergence is estimated.Simulation results are presented to validate strong robustness of the proposed second-order controllers formodel uncertainties and limited perturbationswith the comparison with the standard twisting algorithm.The chattering alleviation and attenuation is also achieved in actuatingmechanism.

spacecrafton-orbit servicing；twisting algorithm；linear compensation；sliding surface；strict Lyapunov function

V448.2

：A

：0367-6234（2015）11-0006-09

10.11918／j.issn.0367-6234.2015.11.002

2014-09-26.

耿云海（1970—），男，教授，博士生导师.

陈炳龙，chenbinglonghit＠163.com.